北师大版八年级数学下册 2.5一元一次不等式与一次函数(第1课时)课件 (共19张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 2.5一元一次不等式与一次函数(第1课时)课件 (共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-13 07:06:14 | ||
图片预览





文档简介
(共19张PPT)
2.5 一元一次不等式与一次
函数
课程讲授
新知导入
随堂练习
课堂小结
第二章 一元一次不等式与
一元一次不等式组
第1课时 一元一次不等式与一次函数
知识要点
一元一次不等式与一次函数的关系
新知导入
想一想:一次函数的图象是__________.它与x轴的交点坐标是 ,与y轴的交点坐标是 ;要作一次函数的图象,只需_______点即可.
一条直线
(0,b)
两
课程讲授
1
一元一次不等式与一次函数的关系
问题1.1:解不等式:5x+6>3x+10.
解:移项,得5x-3x>10-6.
合并同类项,得2x>4.
两边都除以2,得x>2.
课程讲授
1
一元一次不等式与一次函数的关系
问题1.2:当自变量x为何值时,函数y=2x-4值大于0
问题1.1中,不等式可化为2x-4>0,解得x>2.
问题1.2中,是要解不等式2x-4>0,得出x>2 时,函数y=2x-4值大于0.
这两个问题有什么关系
这两个问题实际上就是同一个问题.
课程讲授
1
一元一次不等式与一次函数的关系
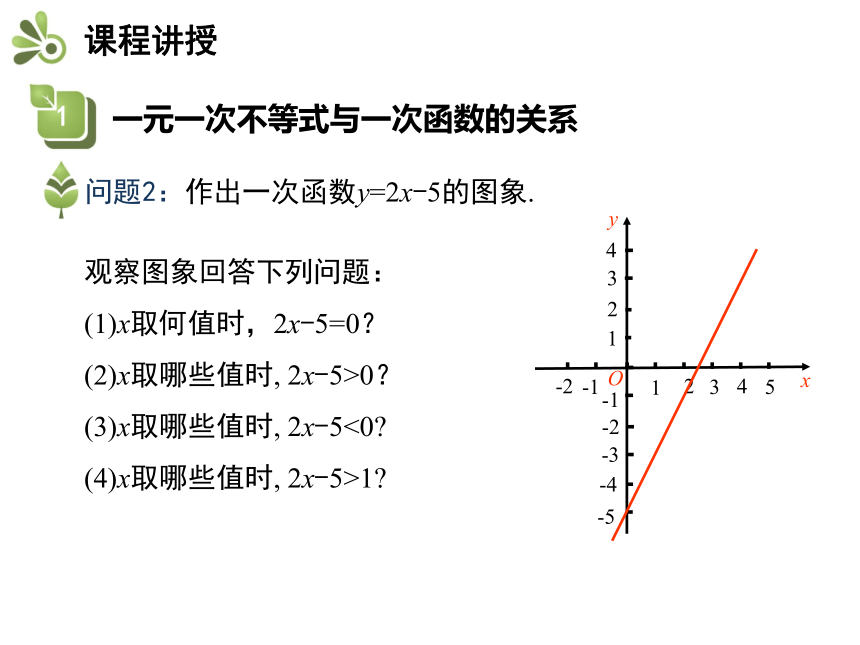
问题2:作出一次函数y=2x-5的图象.
O
1
2
3
4
5
-2
-1
x
2
3
1
4
-3
-5
-2
-4
y
-1
观察图象回答下列问题:
(1)x取何值时,2x-5=0?
(2)x取哪些值时, 2x-5>0?
(3)x取哪些值时, 2x-5<0
(4)x取哪些值时, 2x-5>1
课程讲授
1
一元一次不等式与一次函数的关系
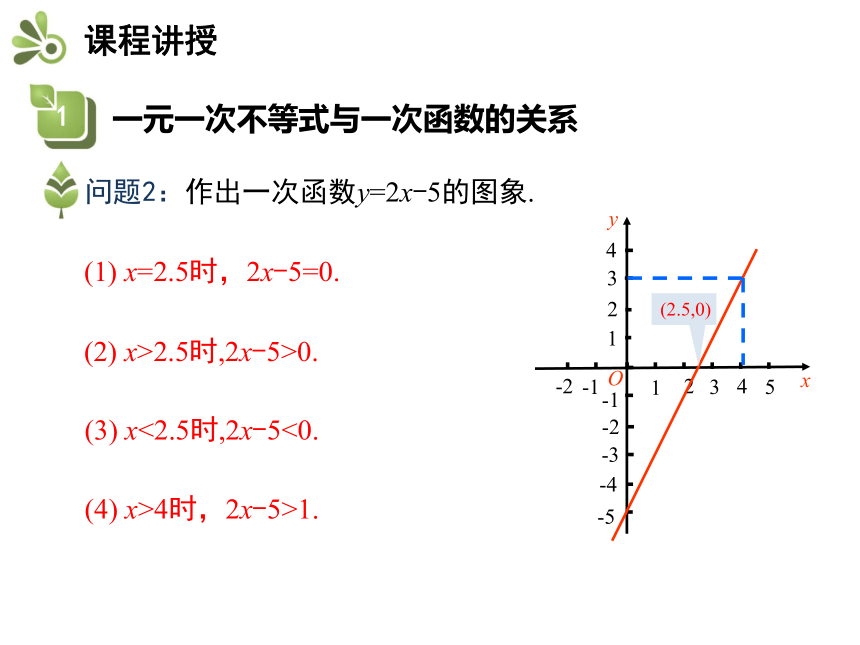
问题2:作出一次函数y=2x-5的图象.
O
1
2
3
4
5
-2
-1
x
2
3
1
4
-3
-5
-2
-4
y
-1
(1) x=2.5时,2x-5=0.
(2.5,0)
(3) x<2.5时,2x-5<0.
(4) x>4时,2x-5>1.
(2) x>2.5时,2x-5>0.
课程讲授
1
一元一次不等式与一次函数的关系
通过对图象的观察、分析,得:
我们既可以运用函数图象解不等式,也可以运用解不等式帮助研究函数问题,二者相互渗透,互相作用.不等式与函数是紧密联系着的一个整体.
课程讲授
1
一元一次不等式与一次函数的关系
例 兄弟俩赛跑,哥哥先让弟弟跑9 m,然后自已才开始跑,已知弟弟每秒跑3 m,哥哥每秒跑4 m.列出函数关系式,作出函数图象,观察图象回答下列问题:
(1)何时弟弟跑在哥哥前面?
(2)何时哥哥跑在弟弟前面?
(3)谁先跑过20 m?谁先跑过100 m?
课程讲授
1
一元一次不等式与一次函数的关系
(1)_______________时,弟弟跑在哥哥前面.
(2)__________时,哥哥跑在弟弟前面.
0(s)x>9(s)
y哥=4x
y弟=3x+9
O
6
8
10
2
x/s
4
12
24
12
30
18
36
6
y/m
42
48
(9,36)
(3)______先跑过20 m.______先跑过100 m.
弟弟
哥哥
课程讲授
1
一元一次不等式与一次函数的关系
归纳:一元一次不等式与一次函数的关系
任何一个一元一次不等式都可以转化为ax+b>0(a≠0)或ax+b<0(a≠0)的形式.因此,解一元一次不等式可以看作:当一次函数y=ax+b(a≠0)的值大于0(或小于0)时,求自变量的取值范围.
课程讲授
1
一元一次不等式与一次函数的关系
拓展归纳 一元一次不等式与一次函数的关系反应在函数图象上,即一次函数y=ax+b(a≠0)的图象在x轴上方时对应横坐标(x的值)的集合,就是不等式ax+b>0(a≠0)的解集;一次函数y=ax+b(a≠0)的图象在x轴下方时对应横坐标(x的值)的集合,就是不等式ax+b<0(a≠0)的解集.
课程讲授
1
一元一次不等式与一次函数的关系
练一练:根据下列一次函数的图象,直接写出下列不等式的解集.
解:(1)3x+6>0,即y>0,x>-2.
(2)3x+6 ≤0,即y≤0,x≤-2.
-2
x
y=3x+6
y
(1)3x+6>0;(2)3x+6 ≤0;
课程讲授
1
一元一次不等式与一次函数的关系
练一练:根据下列一次函数的图象,直接写出下列不等式的解集.
解:(3)–x+3 ≥0,即y≥0,x≤3.
(4)–x+3<0,即y<0,x>3.
x
y
3
y=-x+3
(3) –x+3 ≥0;(4) –x+3<0.
随堂练习
1.已知y1=-x+3, y2=3x-4,当x取哪些值时,y1>y2?你是怎样做的
解:根据题意,得-x+3> 3x-4,
解得
因此,当 时,y1>y2.
随堂练习
2. 甲、乙两辆摩托车从相距20 km的A,B两地相向而行,
图中l1,l2分别表示两辆摩托车离开A地的距离s(km)
与行驶时间t(h)之间函数关系.
(1)哪辆摩托车的速度较快?
(2)经过多长时间,甲车行驶到A,B两地中点?
随堂练习
解:(1)从图象中可知
故摩托车乙速度快.
(2)当s=10km时,
即经过0.3h时,甲车行驶到A、B两地的中点.
随堂练习
3.用画函数图象的方法解不等式5x+4<2x+10.
分析:把不等式转化为一次函数,通过一次函数图象确定不等式的解集.
解:设y1=5x+4,y2=2x+10.在同一个直角
坐标系中,这两个一次函数的图象如图所
示.
由函数图象知,这两个一次函数图象的交
点坐标是(2,14).
当x<2时,y1的解集是x<2.
课堂小结
一元一次不等式
一次函数
通过图象可直接解不等式
可以研究一次函数的图象走向
2.5 一元一次不等式与一次
函数
课程讲授
新知导入
随堂练习
课堂小结
第二章 一元一次不等式与
一元一次不等式组
第1课时 一元一次不等式与一次函数
知识要点
一元一次不等式与一次函数的关系
新知导入
想一想:一次函数的图象是__________.它与x轴的交点坐标是 ,与y轴的交点坐标是 ;要作一次函数的图象,只需_______点即可.
一条直线
(0,b)
两
课程讲授
1
一元一次不等式与一次函数的关系
问题1.1:解不等式:5x+6>3x+10.
解:移项,得5x-3x>10-6.
合并同类项,得2x>4.
两边都除以2,得x>2.
课程讲授
1
一元一次不等式与一次函数的关系
问题1.2:当自变量x为何值时,函数y=2x-4值大于0
问题1.1中,不等式可化为2x-4>0,解得x>2.
问题1.2中,是要解不等式2x-4>0,得出x>2 时,函数y=2x-4值大于0.
这两个问题有什么关系
这两个问题实际上就是同一个问题.
课程讲授
1
一元一次不等式与一次函数的关系
问题2:作出一次函数y=2x-5的图象.
O
1
2
3
4
5
-2
-1
x
2
3
1
4
-3
-5
-2
-4
y
-1
观察图象回答下列问题:
(1)x取何值时,2x-5=0?
(2)x取哪些值时, 2x-5>0?
(3)x取哪些值时, 2x-5<0
(4)x取哪些值时, 2x-5>1
课程讲授
1
一元一次不等式与一次函数的关系
问题2:作出一次函数y=2x-5的图象.
O
1
2
3
4
5
-2
-1
x
2
3
1
4
-3
-5
-2
-4
y
-1
(1) x=2.5时,2x-5=0.
(2.5,0)
(3) x<2.5时,2x-5<0.
(4) x>4时,2x-5>1.
(2) x>2.5时,2x-5>0.
课程讲授
1
一元一次不等式与一次函数的关系
通过对图象的观察、分析,得:
我们既可以运用函数图象解不等式,也可以运用解不等式帮助研究函数问题,二者相互渗透,互相作用.不等式与函数是紧密联系着的一个整体.
课程讲授
1
一元一次不等式与一次函数的关系
例 兄弟俩赛跑,哥哥先让弟弟跑9 m,然后自已才开始跑,已知弟弟每秒跑3 m,哥哥每秒跑4 m.列出函数关系式,作出函数图象,观察图象回答下列问题:
(1)何时弟弟跑在哥哥前面?
(2)何时哥哥跑在弟弟前面?
(3)谁先跑过20 m?谁先跑过100 m?
课程讲授
1
一元一次不等式与一次函数的关系
(1)_______________时,弟弟跑在哥哥前面.
(2)__________时,哥哥跑在弟弟前面.
0(s)
y哥=4x
y弟=3x+9
O
6
8
10
2
x/s
4
12
24
12
30
18
36
6
y/m
42
48
(9,36)
(3)______先跑过20 m.______先跑过100 m.
弟弟
哥哥
课程讲授
1
一元一次不等式与一次函数的关系
归纳:一元一次不等式与一次函数的关系
任何一个一元一次不等式都可以转化为ax+b>0(a≠0)或ax+b<0(a≠0)的形式.因此,解一元一次不等式可以看作:当一次函数y=ax+b(a≠0)的值大于0(或小于0)时,求自变量的取值范围.
课程讲授
1
一元一次不等式与一次函数的关系
拓展归纳 一元一次不等式与一次函数的关系反应在函数图象上,即一次函数y=ax+b(a≠0)的图象在x轴上方时对应横坐标(x的值)的集合,就是不等式ax+b>0(a≠0)的解集;一次函数y=ax+b(a≠0)的图象在x轴下方时对应横坐标(x的值)的集合,就是不等式ax+b<0(a≠0)的解集.
课程讲授
1
一元一次不等式与一次函数的关系
练一练:根据下列一次函数的图象,直接写出下列不等式的解集.
解:(1)3x+6>0,即y>0,x>-2.
(2)3x+6 ≤0,即y≤0,x≤-2.
-2
x
y=3x+6
y
(1)3x+6>0;(2)3x+6 ≤0;
课程讲授
1
一元一次不等式与一次函数的关系
练一练:根据下列一次函数的图象,直接写出下列不等式的解集.
解:(3)–x+3 ≥0,即y≥0,x≤3.
(4)–x+3<0,即y<0,x>3.
x
y
3
y=-x+3
(3) –x+3 ≥0;(4) –x+3<0.
随堂练习
1.已知y1=-x+3, y2=3x-4,当x取哪些值时,y1>y2?你是怎样做的
解:根据题意,得-x+3> 3x-4,
解得
因此,当 时,y1>y2.
随堂练习
2. 甲、乙两辆摩托车从相距20 km的A,B两地相向而行,
图中l1,l2分别表示两辆摩托车离开A地的距离s(km)
与行驶时间t(h)之间函数关系.
(1)哪辆摩托车的速度较快?
(2)经过多长时间,甲车行驶到A,B两地中点?
随堂练习
解:(1)从图象中可知
故摩托车乙速度快.
(2)当s=10km时,
即经过0.3h时,甲车行驶到A、B两地的中点.
随堂练习
3.用画函数图象的方法解不等式5x+4<2x+10.
分析:把不等式转化为一次函数,通过一次函数图象确定不等式的解集.
解:设y1=5x+4,y2=2x+10.在同一个直角
坐标系中,这两个一次函数的图象如图所
示.
由函数图象知,这两个一次函数图象的交
点坐标是(2,14).
当x<2时,y1
课堂小结
一元一次不等式
一次函数
通过图象可直接解不等式
可以研究一次函数的图象走向
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
