人教版六年级下学期数学比例的应用(正比例与反比例)课件(共48张PPT)
文档属性
| 名称 | 人教版六年级下学期数学比例的应用(正比例与反比例)课件(共48张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 16:06:38 | ||
图片预览










文档简介
(共48张PPT)
2022年4月
六年级 比例的应用(正比例与反比例)
课前小练
在行程问题中,如何判断相关联的两个量是成正比例还是成反比例?
课前小练
在行程问题中,如何判断相关联的两个量是成正比例还是成反比例?
路程=速度×时间
当时间一定时,路程和速度成正比例;
当路程一定时,速度和时间成反比例;
当速度一定时,路程和时间成正比例。
知识梳理
正比例与反比例的区别
正比例与反比例的判断方法
关键是看这两个相关联的量中相对应的两个数的商一定还是积一定,如果商一定,
就成正比例;如果积一定,就成反比例。
知识梳理
用正反比例解决问题:
根据问题中的不变量找出两种相关联的量,并正确判断这两种相关联的量成什么比例关系,并根据正、反比例关系式列出相应的方程并求解。
常见的数量关系式:(成正比例或成反比例)
单价×数量=总价
单产量×数量=总产量
速度×时间=路程
工效×工作时间=工作总量
探究一:正反比例概念的应用
例 1:下列关于比例关系的说法正确的是( )。
A.身高和年龄成正比例关系
B.周长一定时,圆周率和半径成反比例关系
C.顺水航行路程一定时,静水速度与时间成反比例关系
D.底面积一定时,长方体的体积与它的高成正比例关系
探究一:正反比例概念的应用
例 1:下列关于比例关系的说法正确的是( )。
A.身高和年龄成正比例关系
身高和年龄不成比例关系, 错误
B.周长一定时,圆周率和半径成反比例关系
圆周率为定值,当周长一定时,它的半径也为定值。错误
C.顺水航行路程一定时,静水速度与时间成反比例关系
D.底面积一定时,长方体的体积与它的高成正比例关系
探究一:正反比例概念的应用
例 1:下列关于比例关系的说法正确的是( )。
A.身高和年龄成正比例关系
B.周长一定时,圆周率和半径成反比例关系
C.顺水航行路程一定时,静水速度与时间成反比例关系
顺水航行的路程=(静水速度+水流速度)×时间,
顺水航行的路程一定,静水速度和时间不成比例关系。错误。
D.底面积一定时,长方体的体积与它的高成正比例关系
探究一:正反比例概念的应用
例 1:下列关于比例关系的说法正确的是( )。
A.身高和年龄成正比例关系
B.周长一定时,圆周率和半径成反比例关系
C.顺水航行路程一定时,静水速度与时间成反比例关系
D.底面积一定时,长方体的体积与它的高成正比例关系
长方体的底面积=长方体的体积÷高
底面积一定时,长方体的体积与它的高成正比例关系,正确。
知识梳理
在判断一个关系中,量与量之间成什么关系时,我们要:
一看,就是看数量关系中,有哪两种相关联的量;
二找,就是从两种相关联的量的关系式中找出定量,找一找,是它们的
商一定,还是它们的积一定,或者是它们的积、商都不一定;
三判,就是判断两种相关联的量成不成比例,成什么比例。如果是商一
定,就成正比例;如果是积一定,就成反比例;如果积、商都不是定量,
就不成比例。
探究二:正比例图像
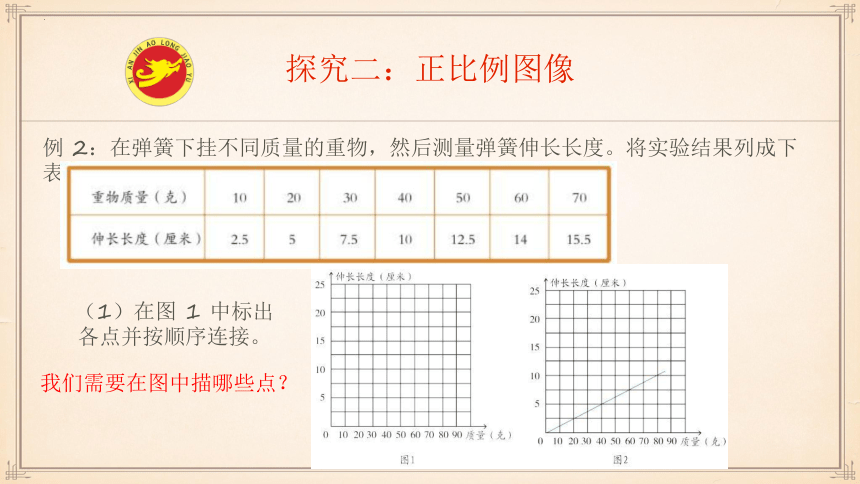
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(1)在图 1 中标出
各点并按顺序连接。
我们需要在图中描哪些点?
探究二:正比例图像
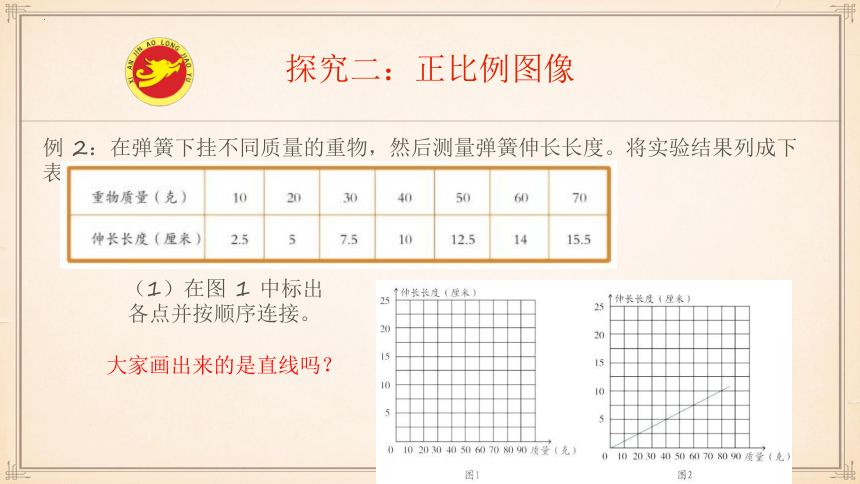
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(1)在图 1 中标出
各点并按顺序连接。
大家画出来的是直线吗?
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(1)在图 1 中标出
各点并按顺序连接。
为什么前面 5 个点连起来的是直线,
而后面变成了折线呢?
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(1)在图 1 中标出
各点并按顺序连接。
我们只看前 5 个点,请想想:弹簧伸长的长度和质量之间成什么比例关系吗?为什么?
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
我们只看前 5 个点,请想想:弹簧伸长的长度和质量之间成什么比例关系吗?为什么?
它们的商都等于 4 是一个定值,所以成正比例关系。
涉及到弹簧的时候,我们一定要强调在一定范围内,弹簧伸长的长度和质量之间成正比例关系。
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
我们只看前 5 个点,请想想:弹簧伸长的长度和质量之间成什么比例关系吗?为什么?
它们的商都等于 4 是一个定值,所以成正比例关系。
劲度系数:它描述单位形变量时所产生弹力的大小。
劲度系数=重物质量÷伸长长度 k=m/L
系数值表示一定范围内,使弹簧伸长(或缩短)1 厘米时所需重物的质量。
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(2)劲度系数,即弹性系数,它描述单位形变量时所产生弹力的大小,系数值表示一定范围内,使弹簧伸长(或缩短)1 厘米时所需重物的质量。
试计算图 1 和图 2 中两种弹簧的劲度系数。
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(2)劲度系数,即弹性系数,它描述单位形变量时所产生弹力的大小,系数值表示一定范围内,使弹簧伸长(或缩短)1 厘米时所需重物的质量。
试计算图 1 和图 2 中两种弹簧的劲度系数。
怎么计算图1、 2 的劲度系数?你在图 1、2 中能找到哪些信息?
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(2)劲度系数,即弹性系数,它描述单位形变量时所产生弹力的大小,系数值表示一定范围内,使弹簧伸长(或缩短)1 厘米时所需重物的质量。
试计算图 1 和图 2 中两种弹簧的劲度系数。
20÷5=4(克)
40÷5=8(克)
答:使图 1 中的弹簧伸长 1 厘米所需重物的质量是 4 克,使图 2 中的弹簧伸长 1 厘米所需重物的质量是 8 克。
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(3)某重物能使图 1 中的弹簧从 5 厘米伸长到 9 厘米,则这个重物能使图2 中的弹簧伸长多少厘米?(弹性范围内)
你能求出这个重物的质量吗?如何算?
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(3)某重物能使图 1 中的弹簧从 5 厘米伸长到 9 厘米,则这个重物能使图2 中的弹簧伸长多少厘米?(弹性范围内)
你能求出这个重物的质量吗?
重物质量=劲度系数×伸长长度
图 1 的劲度系数知道,伸长长度多少?
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(3)某重物能使图 1 中的弹簧从 5 厘米伸长到 9 厘米,则这个重物能使图2 中的弹簧伸长多少厘米?(弹性范围内)
(3)9-5=4(厘米)
4×4=16(克)
16÷8=2(厘米)
答:这个重物能使图 2 中的弹簧伸长 2 厘米。
知识梳理
理解劲度系数是解决本题的关键,注意弹簧伸长的长度与重物质量成正比例关系,这个关系成立的前提是弹簧没有变形的情况下。
重物质量=劲度系数×伸长长度
劲度系数=重物质量÷伸长长度
探究三:正反比例图像的应用
例 3:观察下面两个表,完成问题。
(1)根据上表中的数据,分别在下面的图 1、图 2 中找出各点,并顺次连接各点。
探究三:正反比例图像的应用
例 3:观察下面两个表,完成问题。
(1)根据上表中的数据,分别在下面的图 1、图 2 中找出各点,并顺次连接各点。
探究三:正反比例图像的应用
例 3:观察下面两个表,完成问题。
(2)图 1 中两个量成( )比例关系,图 2 中两个量成( )比例关系。
如何判断图1、图2中两个量的关系?
探究三:正反比例图像的应用
例 3:观察下面两个表,完成问题。
(2)图 1 中两个量成( )比例关系,图 2 中两个量成( )比例关系。
如何判断图1、图2中两个量的关系?
图1:路程÷时间=40
路程和时间成正比例关系。
图2:速度×时间=120
速度和时间成反比例关系。
探究三:正反比例图像的应用
例 3:观察下面两个表,完成问题。
(3)在图 1 中,行驶 100 千米需要多少小时?
(4)在图 2 中,如果想要 2.5 小时行完全程,每小时需要行多少千米?
探究三:正反比例图像的应用
例 3:观察下面两个表,完成问题。
(3)在图 1 中,行驶 100 千米需要多少小时?
(4)在图 2 中,如果想要 2.5 小时行完全程,每小时需要行多少千米?
3)40÷1=40(千米/时)
100÷40=2.5(小时)
答:行驶 100 千米需要 2.5 小时。
(4)120×1=120(千米)
120÷2.5=48(千米/时)
答:每小时需要行 48 千米。
知识梳理
行程问题中,速度一定时,路程和时间成正比例关系,
路程一定时,速度和时间成反比例关系。
正比例的图象是一条直线,反比例的图象是一条平滑曲线。
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(1)请把表格填写完整。
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(1)请把表格填写完整。
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(2)x 与 z 成什么比例关系?
如何判断 x 与 z 成什么比例关系?
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(2)x 与 z 成什么比例关系?
如何判断 x 与 z 成什么比例关系?
看x÷z等于定值,还是 xz 等于定值。
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(2)x 与 z 成什么比例关系?
如何判断 x 与 z 成什么比例关系?
看x÷z等于定值,还是 xz 等于定值。
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(3)如果有一个量 m 与 x,y,z 都有关联,且 m 与 z 成反比例关系,那么 m 与 x,y 分别成什么比例关系?
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(3)如果有一个量 m 与 x,y,z 都有关联,且 m 与 z 成反比例关系,那么 m 与 x,y 分别成什么比例关系?
z作为桥梁,z分别与m和x有关系。
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(3)如果有一个量 m 与 x,y,z 都有关联,且 m 与 z 成反比例关系,那么 m 与 x,y 分别成什么比例关系?
z作为桥梁,z分别与m和x有关系。
已经知道了 xz=8,mz=k, k一定,想办法消掉z,得到 m 与 x 的关系。
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(3)如果有一个量 m 与 x,y,z 都有关联,且 m 与 z 成反比例关系,那么 m 与 x,y 分别成什么比例关系?
知道 y 与 z 成反比例关系,从表格中得到 yz=12, mz=k, k一定,想办法消掉 z,得到 m 与 y 的关系。
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(3)如果有一个量 m 与 x,y,z 都有关联,且 m 与 z 成反比例关系,那么 m 与 x,y 分别成什么比例关系?
知识梳理
x、y 成正比例,y、z 成反比例 ,x、z 成反比例
x、z 成反比例,m、z 成反比例, m、x 成正比例
y、z 成反比例,m、z 成反比例 ,m、y 成正比例
x、y 成正比例,y、z 成正比例, x、z 成正比例
如果 x、y 和 y、z 都成反比例(或正比例),则 x、z 成正比例;
如果 x、y 和 y、z 一个成正比例,一个成反比例,则 x、z 成反比例。
知识梳理
x、y 成正比例,y、z 成反比例 ,x、z 成反比例
x、z 成反比例,m、z 成反比例, m、x 成正比例
y、z 成反比例,m、z 成反比例 ,m、y 成正比例
x、y 成正比例,y、z 成正比例, x、z 成正比例
如果 x、y 和 y、z 都成反比例(或正比例),则 x、z 成正比例;
如果 x、y 和 y、z 一个成正比例,一个成反比例,则 x、z 成反比例。
判断多个相关联的量之间的比例关系:消去无关的未知数,找到要判断的两个量的关系。
如果是填空或选择题,我们可以直接应用刚才得出的结论。
作 业
写出一个数量关系式,并分别之处其中成正比例关系和反比例关系的两个量。
下列各式中,非零数x与y成正比例关系的是( )
3. 3.如果 x,y,m,n 是四个有关联的量,它们的关系是
x=4y=m+3=8÷n,x和 m( )关系;y 和 n( )关系;x 和 y( )关系。
(填“成正比例”、“成反比例”或“不成比例”)
作 业
4.某商店想把A,B两种巧克力等质量混合售卖,经调查,A种巧克力的销售情况如下表:
周一 周二 周三 周四 周五
收入(元) 25 50 75 100 125
质量(千克) 1 2 3 4 5
(1)在图中找出表中的对应的点,顺次连接并延长,表中两个量成( )比例关系。
(2)图中直线表示混合后巧克力的收入与质量关系图,请计算B种巧克力的单价,并在图中画出B种巧克力的收入与质量关系图。
作 业
5.a,b,c,d 是四个相关联的量,已知 a,b 成正比例,b 的倒数与 c 成反
比例,c 与 d 的倒数成反比例,那么 a 与 d 之间是什么比例关系?
知识总结
1.正比例关系:如果用字母 y 和 x 表示两种相关联的量,用 k 表示它们的比
值(一定),那么有y÷k=x(如图 1)。
2.反比例关系:如果用字母 y 和 x 表示两种相关联的量,用 k 表示它们的积
(一定),那么有 xy k (如图 2)。
3.判断多个相关联的量之间的比例关系:消去无关的未知量,找到要判断
的两个量的关系。
作业答案
作业答案
2022年4月
六年级 比例的应用(正比例与反比例)
课前小练
在行程问题中,如何判断相关联的两个量是成正比例还是成反比例?
课前小练
在行程问题中,如何判断相关联的两个量是成正比例还是成反比例?
路程=速度×时间
当时间一定时,路程和速度成正比例;
当路程一定时,速度和时间成反比例;
当速度一定时,路程和时间成正比例。
知识梳理
正比例与反比例的区别
正比例与反比例的判断方法
关键是看这两个相关联的量中相对应的两个数的商一定还是积一定,如果商一定,
就成正比例;如果积一定,就成反比例。
知识梳理
用正反比例解决问题:
根据问题中的不变量找出两种相关联的量,并正确判断这两种相关联的量成什么比例关系,并根据正、反比例关系式列出相应的方程并求解。
常见的数量关系式:(成正比例或成反比例)
单价×数量=总价
单产量×数量=总产量
速度×时间=路程
工效×工作时间=工作总量
探究一:正反比例概念的应用
例 1:下列关于比例关系的说法正确的是( )。
A.身高和年龄成正比例关系
B.周长一定时,圆周率和半径成反比例关系
C.顺水航行路程一定时,静水速度与时间成反比例关系
D.底面积一定时,长方体的体积与它的高成正比例关系
探究一:正反比例概念的应用
例 1:下列关于比例关系的说法正确的是( )。
A.身高和年龄成正比例关系
身高和年龄不成比例关系, 错误
B.周长一定时,圆周率和半径成反比例关系
圆周率为定值,当周长一定时,它的半径也为定值。错误
C.顺水航行路程一定时,静水速度与时间成反比例关系
D.底面积一定时,长方体的体积与它的高成正比例关系
探究一:正反比例概念的应用
例 1:下列关于比例关系的说法正确的是( )。
A.身高和年龄成正比例关系
B.周长一定时,圆周率和半径成反比例关系
C.顺水航行路程一定时,静水速度与时间成反比例关系
顺水航行的路程=(静水速度+水流速度)×时间,
顺水航行的路程一定,静水速度和时间不成比例关系。错误。
D.底面积一定时,长方体的体积与它的高成正比例关系
探究一:正反比例概念的应用
例 1:下列关于比例关系的说法正确的是( )。
A.身高和年龄成正比例关系
B.周长一定时,圆周率和半径成反比例关系
C.顺水航行路程一定时,静水速度与时间成反比例关系
D.底面积一定时,长方体的体积与它的高成正比例关系
长方体的底面积=长方体的体积÷高
底面积一定时,长方体的体积与它的高成正比例关系,正确。
知识梳理
在判断一个关系中,量与量之间成什么关系时,我们要:
一看,就是看数量关系中,有哪两种相关联的量;
二找,就是从两种相关联的量的关系式中找出定量,找一找,是它们的
商一定,还是它们的积一定,或者是它们的积、商都不一定;
三判,就是判断两种相关联的量成不成比例,成什么比例。如果是商一
定,就成正比例;如果是积一定,就成反比例;如果积、商都不是定量,
就不成比例。
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(1)在图 1 中标出
各点并按顺序连接。
我们需要在图中描哪些点?
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(1)在图 1 中标出
各点并按顺序连接。
大家画出来的是直线吗?
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(1)在图 1 中标出
各点并按顺序连接。
为什么前面 5 个点连起来的是直线,
而后面变成了折线呢?
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(1)在图 1 中标出
各点并按顺序连接。
我们只看前 5 个点,请想想:弹簧伸长的长度和质量之间成什么比例关系吗?为什么?
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
我们只看前 5 个点,请想想:弹簧伸长的长度和质量之间成什么比例关系吗?为什么?
它们的商都等于 4 是一个定值,所以成正比例关系。
涉及到弹簧的时候,我们一定要强调在一定范围内,弹簧伸长的长度和质量之间成正比例关系。
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
我们只看前 5 个点,请想想:弹簧伸长的长度和质量之间成什么比例关系吗?为什么?
它们的商都等于 4 是一个定值,所以成正比例关系。
劲度系数:它描述单位形变量时所产生弹力的大小。
劲度系数=重物质量÷伸长长度 k=m/L
系数值表示一定范围内,使弹簧伸长(或缩短)1 厘米时所需重物的质量。
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(2)劲度系数,即弹性系数,它描述单位形变量时所产生弹力的大小,系数值表示一定范围内,使弹簧伸长(或缩短)1 厘米时所需重物的质量。
试计算图 1 和图 2 中两种弹簧的劲度系数。
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(2)劲度系数,即弹性系数,它描述单位形变量时所产生弹力的大小,系数值表示一定范围内,使弹簧伸长(或缩短)1 厘米时所需重物的质量。
试计算图 1 和图 2 中两种弹簧的劲度系数。
怎么计算图1、 2 的劲度系数?你在图 1、2 中能找到哪些信息?
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(2)劲度系数,即弹性系数,它描述单位形变量时所产生弹力的大小,系数值表示一定范围内,使弹簧伸长(或缩短)1 厘米时所需重物的质量。
试计算图 1 和图 2 中两种弹簧的劲度系数。
20÷5=4(克)
40÷5=8(克)
答:使图 1 中的弹簧伸长 1 厘米所需重物的质量是 4 克,使图 2 中的弹簧伸长 1 厘米所需重物的质量是 8 克。
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(3)某重物能使图 1 中的弹簧从 5 厘米伸长到 9 厘米,则这个重物能使图2 中的弹簧伸长多少厘米?(弹性范围内)
你能求出这个重物的质量吗?如何算?
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(3)某重物能使图 1 中的弹簧从 5 厘米伸长到 9 厘米,则这个重物能使图2 中的弹簧伸长多少厘米?(弹性范围内)
你能求出这个重物的质量吗?
重物质量=劲度系数×伸长长度
图 1 的劲度系数知道,伸长长度多少?
探究二:正比例图像
例 2:在弹簧下挂不同质量的重物,然后测量弹簧伸长长度。将实验结果列成下表:
(3)某重物能使图 1 中的弹簧从 5 厘米伸长到 9 厘米,则这个重物能使图2 中的弹簧伸长多少厘米?(弹性范围内)
(3)9-5=4(厘米)
4×4=16(克)
16÷8=2(厘米)
答:这个重物能使图 2 中的弹簧伸长 2 厘米。
知识梳理
理解劲度系数是解决本题的关键,注意弹簧伸长的长度与重物质量成正比例关系,这个关系成立的前提是弹簧没有变形的情况下。
重物质量=劲度系数×伸长长度
劲度系数=重物质量÷伸长长度
探究三:正反比例图像的应用
例 3:观察下面两个表,完成问题。
(1)根据上表中的数据,分别在下面的图 1、图 2 中找出各点,并顺次连接各点。
探究三:正反比例图像的应用
例 3:观察下面两个表,完成问题。
(1)根据上表中的数据,分别在下面的图 1、图 2 中找出各点,并顺次连接各点。
探究三:正反比例图像的应用
例 3:观察下面两个表,完成问题。
(2)图 1 中两个量成( )比例关系,图 2 中两个量成( )比例关系。
如何判断图1、图2中两个量的关系?
探究三:正反比例图像的应用
例 3:观察下面两个表,完成问题。
(2)图 1 中两个量成( )比例关系,图 2 中两个量成( )比例关系。
如何判断图1、图2中两个量的关系?
图1:路程÷时间=40
路程和时间成正比例关系。
图2:速度×时间=120
速度和时间成反比例关系。
探究三:正反比例图像的应用
例 3:观察下面两个表,完成问题。
(3)在图 1 中,行驶 100 千米需要多少小时?
(4)在图 2 中,如果想要 2.5 小时行完全程,每小时需要行多少千米?
探究三:正反比例图像的应用
例 3:观察下面两个表,完成问题。
(3)在图 1 中,行驶 100 千米需要多少小时?
(4)在图 2 中,如果想要 2.5 小时行完全程,每小时需要行多少千米?
3)40÷1=40(千米/时)
100÷40=2.5(小时)
答:行驶 100 千米需要 2.5 小时。
(4)120×1=120(千米)
120÷2.5=48(千米/时)
答:每小时需要行 48 千米。
知识梳理
行程问题中,速度一定时,路程和时间成正比例关系,
路程一定时,速度和时间成反比例关系。
正比例的图象是一条直线,反比例的图象是一条平滑曲线。
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(1)请把表格填写完整。
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(1)请把表格填写完整。
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(2)x 与 z 成什么比例关系?
如何判断 x 与 z 成什么比例关系?
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(2)x 与 z 成什么比例关系?
如何判断 x 与 z 成什么比例关系?
看x÷z等于定值,还是 xz 等于定值。
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(2)x 与 z 成什么比例关系?
如何判断 x 与 z 成什么比例关系?
看x÷z等于定值,还是 xz 等于定值。
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(3)如果有一个量 m 与 x,y,z 都有关联,且 m 与 z 成反比例关系,那么 m 与 x,y 分别成什么比例关系?
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(3)如果有一个量 m 与 x,y,z 都有关联,且 m 与 z 成反比例关系,那么 m 与 x,y 分别成什么比例关系?
z作为桥梁,z分别与m和x有关系。
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(3)如果有一个量 m 与 x,y,z 都有关联,且 m 与 z 成反比例关系,那么 m 与 x,y 分别成什么比例关系?
z作为桥梁,z分别与m和x有关系。
已经知道了 xz=8,mz=k, k一定,想办法消掉z,得到 m 与 x 的关系。
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(3)如果有一个量 m 与 x,y,z 都有关联,且 m 与 z 成反比例关系,那么 m 与 x,y 分别成什么比例关系?
知道 y 与 z 成反比例关系,从表格中得到 yz=12, mz=k, k一定,想办法消掉 z,得到 m 与 y 的关系。
探究四:多个量之间的比例关系判断
例 4:下表中的 x,y,z 是三个相关联的量,其中 x 与 y 成正比例,y 与 z成反比例:
(3)如果有一个量 m 与 x,y,z 都有关联,且 m 与 z 成反比例关系,那么 m 与 x,y 分别成什么比例关系?
知识梳理
x、y 成正比例,y、z 成反比例 ,x、z 成反比例
x、z 成反比例,m、z 成反比例, m、x 成正比例
y、z 成反比例,m、z 成反比例 ,m、y 成正比例
x、y 成正比例,y、z 成正比例, x、z 成正比例
如果 x、y 和 y、z 都成反比例(或正比例),则 x、z 成正比例;
如果 x、y 和 y、z 一个成正比例,一个成反比例,则 x、z 成反比例。
知识梳理
x、y 成正比例,y、z 成反比例 ,x、z 成反比例
x、z 成反比例,m、z 成反比例, m、x 成正比例
y、z 成反比例,m、z 成反比例 ,m、y 成正比例
x、y 成正比例,y、z 成正比例, x、z 成正比例
如果 x、y 和 y、z 都成反比例(或正比例),则 x、z 成正比例;
如果 x、y 和 y、z 一个成正比例,一个成反比例,则 x、z 成反比例。
判断多个相关联的量之间的比例关系:消去无关的未知数,找到要判断的两个量的关系。
如果是填空或选择题,我们可以直接应用刚才得出的结论。
作 业
写出一个数量关系式,并分别之处其中成正比例关系和反比例关系的两个量。
下列各式中,非零数x与y成正比例关系的是( )
3. 3.如果 x,y,m,n 是四个有关联的量,它们的关系是
x=4y=m+3=8÷n,x和 m( )关系;y 和 n( )关系;x 和 y( )关系。
(填“成正比例”、“成反比例”或“不成比例”)
作 业
4.某商店想把A,B两种巧克力等质量混合售卖,经调查,A种巧克力的销售情况如下表:
周一 周二 周三 周四 周五
收入(元) 25 50 75 100 125
质量(千克) 1 2 3 4 5
(1)在图中找出表中的对应的点,顺次连接并延长,表中两个量成( )比例关系。
(2)图中直线表示混合后巧克力的收入与质量关系图,请计算B种巧克力的单价,并在图中画出B种巧克力的收入与质量关系图。
作 业
5.a,b,c,d 是四个相关联的量,已知 a,b 成正比例,b 的倒数与 c 成反
比例,c 与 d 的倒数成反比例,那么 a 与 d 之间是什么比例关系?
知识总结
1.正比例关系:如果用字母 y 和 x 表示两种相关联的量,用 k 表示它们的比
值(一定),那么有y÷k=x(如图 1)。
2.反比例关系:如果用字母 y 和 x 表示两种相关联的量,用 k 表示它们的积
(一定),那么有 xy k (如图 2)。
3.判断多个相关联的量之间的比例关系:消去无关的未知量,找到要判断
的两个量的关系。
作业答案
作业答案
