九年级上册数学第二十六章二次函数单元测试二(附答案)
文档属性
| 名称 | 九年级上册数学第二十六章二次函数单元测试二(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 269.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-17 15:47:21 | ||
图片预览




文档简介
九年级上册数学第二十六章二次函数单元测试二(附答案)
学校:___________姓名:___________班级:___________考号:___________
题号
一
二
三
四
五
总分
得分
一、选择题
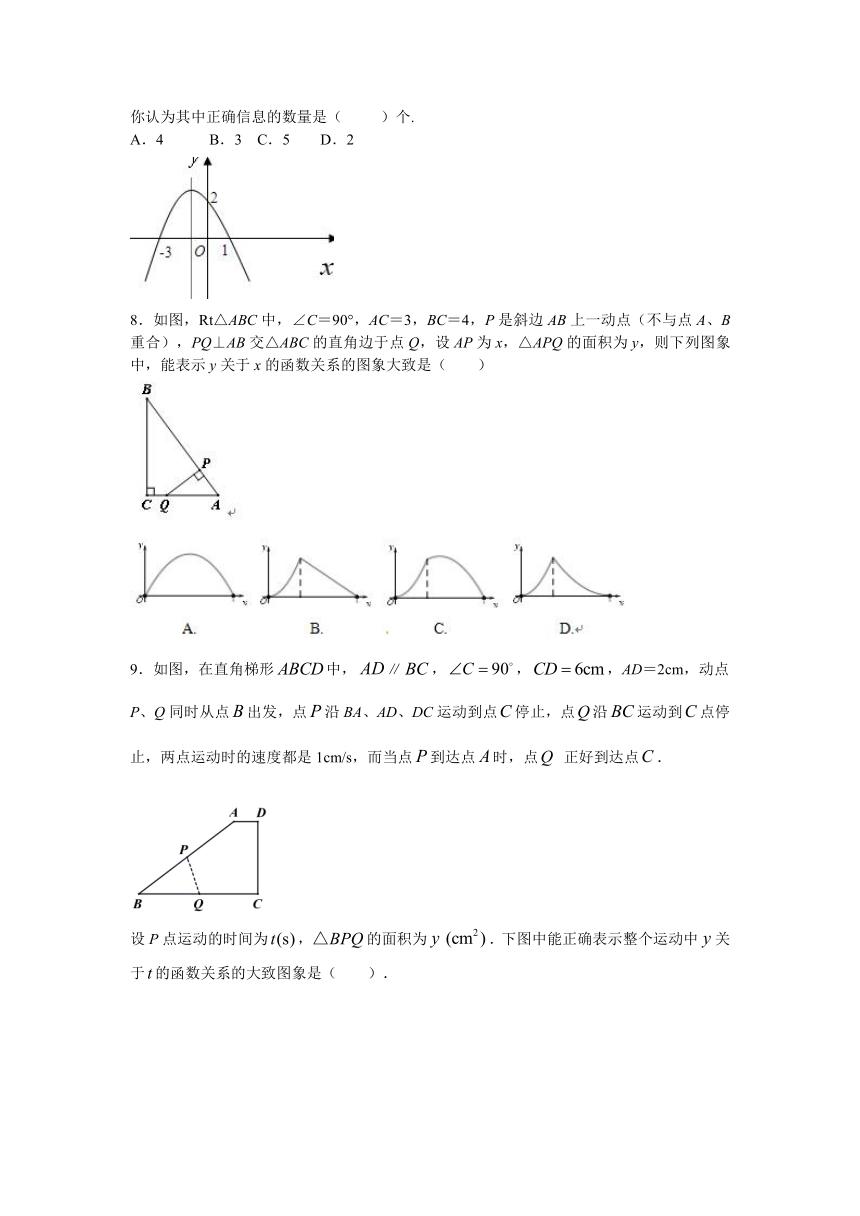
1.如图,在平面直角坐标系中,二次函数y=ax2+mc(a≠0)的 图像经过正方形ABOC的三个顶点,且ac=-2,则m的值为( )
A.1 B.-1 C.2 D.-2
2.抛物线的对称轴是( )
A.直线 B.直线 C.直线 D.直线
8. 抛物线的顶点坐标是 ( )
A. (-5,-2) B. C. D. (-5,2)
A.直线 B.直线 C.直线 D.直线
5. 已知函数①,②,③,④,⑤,其中二次函数的个数为( ).
A.1 B.2 C.3 D.4
6.若A,B(),C为二次函数的图象上的三点,则的大小关系是( )
A. B. C. D.
7.二次函数y=ax2+bx +c的图象如图所示观察图象得出了下面5条信息:( )
(1)<0;(2)图象的对称轴为直线; (3)<0;(4) >0;(5)时,;21世纪教育网
你认为其中正确信息的数量是( )个.
A.4 B.3 C.5 D.2
8.如图,Rt△ABC中,∠C=90°,AC=3,BC=4,P是斜边AB上一动点(不与点A、B重合),PQ⊥AB交△ABC的直角边于点Q,设AP为x,△APQ的面积为y,则下列图象中,能表示y关于x的函数关系的图象大致是( )
9.如图,在直角梯形中,∥,,,AD=2cm,动点P、Q同时从点出发,点沿BA、AD、DC运动到点停止,点沿运动到点停止,两点运动时的速度都是1cm/s,而当点到达点时,点 正好到达点.
设P点运动的时间为,的面积为.下图中能正确表示整个运动中关于的函数关系的大致图象是( ).
10.抛物线图象如图所示,则一次函数与反比例函数在同一坐标系内的图象大致为( )
二、填空题
11.一个y关于x的函数同时满足两个条件:①图象过(2, 1)点;②当x>0时,y随x的增大而减小.这个函数解析式为_________________________(写出一个即可)
12..抛物线如图所示,则它关于轴对称的抛物线的解析式是 .
13.在直角坐标系中,抛物线与x轴交于点A,B(点A在点B的左侧),与y轴交于点C。如果点M在y轴的右侧的抛物线上,,那么点M的坐标为
14.请你选择你喜欢的a、b、c值,使二次函数y=ax2+bx+c(a≠0)的图象同时满足下列条件:
①开口方向向下;②当x<2时,y随x的增大而增大;当x>2时,y随x的增大而减小.这样的二次函数的解析式可以为 .
15.已知:抛物线与y轴交于C点,顶点为M,直线CM的解析式为 并且线段CM的长为,则抛物线的解析式为__________________________.
16.将抛物线的图象向上平移3个单位,则平移后的抛物线C1的解析式为 ,再将C1以原点为中心,旋转180度所得抛物线C2的解析式为_________________
三、计算题
17.(本小题满分12分)
如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA=16 cm, OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒2 cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1 cm的速度匀速运动.设运动时间为t秒.
(1)用含t的式子表示△OPQ的面积S;
(2)判断四边形OPBQ的面积是否是一个定值,如果是,请求出这个定值;如果不是,请说明理由;
(3)当△OPQ∽△ABP时,抛物线y=x2+bx+c经过B、P两点,求抛物线的解析式;
(4)在(3)的条件下,过线段BP上一动点M作轴的平
行线交抛物线于N,求线段MN的最大值.
如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的二次函数图像经过点B、D.
18.请直接写出用m表示点A、D的坐标
19.求这个二次函数的解析式;
20.点Q为二次函数图像上点P至点B之间的一点,连结PQ、BQ,求四边形ABQP面积的最大值.
四、解答题
21.已知:直角坐标平面内有点,过原点的直线,且与过点、的抛物线相交于第一象限的点,若.
(1)求抛物线的解析式;
(2)作轴于点,设有直线交直线于,交抛物线于点,若、、、组成的四边形是平行四边形,求的值。
22.已知二次函数y=x2+2x+m的图象C1与x轴有且只有一个公共点.
(1)求C1的顶点坐标;
(2)将C1向下平移若干个单位后,得抛物线C2,如果C2与x轴的一个交点为A(﹣3,0),求C2的函数关系式,并求C2与x轴的另一个交点坐标;
23.规律是数学研究的重要内容之一.
初中数学中研究的规律主要有一些特定的规则、符号(数)及其运算规律、图形的数值特征和位置关系特征等方面.请你解决以下与数的表示和运算相关的问题:
(1)写出奇数a用整数n表示的式子;
(2)写出有理数b用整数m和整数n表示的式子;
(3)函数的研究中,应关注y随x变化而变化的数值规律(课本里研究函数图象的特征实际上也是为了说明函数的数值规律).
下面对函数的某种数值变化规律进行初步研究:
0
1
2
3
4
5
...
0
1[
4
9
16
25
...
1
3
5
7
9
11
...
由表看出,当x的取值从0开始每增加1个单位时,y的值依次增加1,3,5...
请回答:
①当x的取值从0开始每增加个单位时,y的值变化规律是什么?
②当x的取值从0开始每增加个单位时,y的值变化规律是什么?
24.如图所示,在平面直角坐标系xOy中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.
(1)求抛物线的解析式.
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动,同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
①移动开始后第t秒时,设△PBQ的面积为S,试写出S与t之间的函数关系式,并写出t的取值范围.
②当S取得最大值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
25.我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形,不妨简称为“锅线”,锅口直径为6dm,锅深3dm,锅盖高1dm(锅口直径与锅盖直径视为相同),建立直接坐标系如图①所示,如果把锅纵断面的抛物线的记为C1,把锅盖纵断面的抛物线记为C2.
(1)求C1和C2的解析式;
(2)如图②,过点B作直线BE:y=x﹣1交C1于点E(﹣2,﹣),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;
(3)如果(2)中的直线BE保持不变,抛物线C1或C2上是否存在一点Q,使得△EBQ的面积最大?若存在,求出Q的坐标和△EBQ面积的最大值;若不存在,请说明理由.
26. 某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。 求:(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?(2)每件衬衫降价多少元时,商场平均每天赢利最多?
27.如图,在平面直角坐标系xOy中,四边形ABCD是菱形,顶点A.C.D均在坐标轴上,且AB=5,sinB=.
(1)求过A.C. D三点的抛物线的解析式;
(2)记直线AB的解析式为y1=mx+n,(1)中抛物线的解析式为y2=ax2+bx+c,求当y1<y2时,自变量x的取值范围;
(3)设直线AB与(1)中抛物线的另一个交点为E,P点为抛物线上A.E两点之间的一个动点,当P点在何处时,△PAE的面积最大?并求出面积的最大值.
参考答案
1.A
2.C
3.C
4.B
5.B
6.B
7.A
8. C
9. B
10. D
11.如:等,写出一个即可
12.
13.(4,6)或(1,-6)
14.
15.或
14.
17.
∴当m=-=10时,MN有最大值是9 …………………12分
18.A(3-m,0),D(0,m-3 )
19.设以P(1,0)为顶点的抛物线的解析式为y=a(x-1)2(a≠0)
∵抛物线过点B、D,
∴ 解得 …………4分
所以二次函数的解析式为y=(x-1)2,
即:y=x2-2x+1 …………5分
20.设点Q的坐标为(x,x2-2 x+1),显然1<x<3 …6分
连结BP,过点Q作QH⊥x轴,交BP于点H.
∵A(-1,0),P(1,0),B(3,4)
∴AP=2,BC=3,PC=2
由P(1,0),B(3,4)求得直线BP的解析式为y=2x-2
∵QH⊥x轴,点Q的坐标为(x,x2-2 x+1)
∴点H的横坐标为x,∴点H的坐标为(x,2x-2)
∴QH=2x-2-(x2-2x+1)=-x2+4x-3 …………7分
∴四边形ABQP面积S=S△APB+S△QPB=×AP×BC+×QH×PC
=×2×4+×(-x2+4x-3)×2
=-x2+4x+1=-(x-2)2+5 …………9分
∵1<x<3
∴当x=2时,S取得最大值为5, …………10分
即当点Q的坐标为(2,1)时,四边形ABQP面积的最大值为5
21.(1)解:过点A作AH⊥x轴于点H,过点B作BC⊥x轴于点C,
由点A(-1,2)可得 AH=2,OH=1
由直线OB⊥OA,可得△AHO∽△OCB,
∴ ,
∵OB=2OA,∴OC=4,BC=2 ,∴B(4,2)
设经过点A、O、B的抛物线解析式为
∴ )
解得, ∴抛物线解析式为:
(2)设直线l的解析式为
∵ 直线l经过点B(4,2), ∴ 直线l的解析式为
∵ 直线x=m(m>0)交直线l于,交抛物线于点Q,
∴ 设P点坐标为(m,m),点Q坐标为(m,),
∵由B、C、P、Q四点组成的四边形是平行四边形,∴ PQ//BC且PQ=BC
即: ,
解得或, ∵ m>0 ∴或2
22.解:(1)y=x2+2x+m=(x+1)2+m﹣1,对称轴为x=﹣1,
∵与x轴有且只有一个公共点,
∴顶点的纵坐标为0,
∴C1的顶点坐标为(﹣1,0);
(2)设C2的函数关系式为y=(x+1)2+k,
把A(﹣3,0)代入上式得(﹣3+1)2+k=0,得k=﹣4,
∴C2的函数关系式为y=(x+1)2﹣4.
∵抛物线的对称轴为x=﹣1,与x轴的一个交点为A(﹣3,0),
由对称性可知,它与x轴的另一个交点坐标为(1,0)
23.(1)2n+1(2)b=m/n (n≠0)(3) ①值依次增加、、·····②依次增加、、·····
24.(1)(2)①S=(t-3)2+9(0<t<6)②点R坐标为(3,﹣18)
25.(1)y=x2﹣3(﹣3≤x≤3),y=﹣x2+1(﹣3≤x≤3)(2)P1(,0)、P2(﹣,0)(3)(),
26.(1)20元(2)15元
27.解:(1)∵四边形ABCD是菱形,
∴AB=AD=CD=BC=5,sinB=sinD=;
Rt△OCD中,OC=CD?sinD=4,OD=3;
OA=AD﹣OD=2,即:
A(﹣2,0)、B(﹣5,4)、C(0,4)、D(3,0);
设抛物线的解析式为:y=a(x+2)(x﹣3),得:
2×(﹣3)a=4,a=﹣;
∴抛物线:y=﹣x2+x+4.
(2)由A(﹣2,0)、B(﹣5,4)得直线AB:y1=﹣x﹣;
由(1)得:y2=﹣x2+x+4,则:
,解得:,;
由图可知:当y1<y2时,﹣2<x<5.
(3)∵S△APE=AE?h,
∴当P到直线AB的距离最远时,S△ABC最大;
若设直线L∥AB,则直线L与抛物线有且只有一个交点时,该交点为点P;
设直线L:y=﹣x+b,当直线L与抛物线有且只有一个交点时,
﹣x+b=﹣x2+x+4,且△=0;
求得:b=,即直线L:y=﹣x+;
可得点P(,).
由(2)得:E(5,﹣),则直线PE:y=﹣x+9;
则点F(,0),AF=OA+OF=;
∴△PAE的最大值:S△PAE=S△PAF+S△AEF=××(+)=.
综上所述,当P(,)时,△PAE的面积最大,为.
学校:___________姓名:___________班级:___________考号:___________
题号
一
二
三
四
五
总分
得分
一、选择题
1.如图,在平面直角坐标系中,二次函数y=ax2+mc(a≠0)的 图像经过正方形ABOC的三个顶点,且ac=-2,则m的值为( )
A.1 B.-1 C.2 D.-2
2.抛物线的对称轴是( )
A.直线 B.直线 C.直线 D.直线
8. 抛物线的顶点坐标是 ( )
A. (-5,-2) B. C. D. (-5,2)
A.直线 B.直线 C.直线 D.直线
5. 已知函数①,②,③,④,⑤,其中二次函数的个数为( ).
A.1 B.2 C.3 D.4
6.若A,B(),C为二次函数的图象上的三点,则的大小关系是( )
A. B. C. D.
7.二次函数y=ax2+bx +c的图象如图所示观察图象得出了下面5条信息:( )
(1)<0;(2)图象的对称轴为直线; (3)<0;(4) >0;(5)时,;21世纪教育网
你认为其中正确信息的数量是( )个.
A.4 B.3 C.5 D.2
8.如图,Rt△ABC中,∠C=90°,AC=3,BC=4,P是斜边AB上一动点(不与点A、B重合),PQ⊥AB交△ABC的直角边于点Q,设AP为x,△APQ的面积为y,则下列图象中,能表示y关于x的函数关系的图象大致是( )
9.如图,在直角梯形中,∥,,,AD=2cm,动点P、Q同时从点出发,点沿BA、AD、DC运动到点停止,点沿运动到点停止,两点运动时的速度都是1cm/s,而当点到达点时,点 正好到达点.
设P点运动的时间为,的面积为.下图中能正确表示整个运动中关于的函数关系的大致图象是( ).
10.抛物线图象如图所示,则一次函数与反比例函数在同一坐标系内的图象大致为( )
二、填空题
11.一个y关于x的函数同时满足两个条件:①图象过(2, 1)点;②当x>0时,y随x的增大而减小.这个函数解析式为_________________________(写出一个即可)
12..抛物线如图所示,则它关于轴对称的抛物线的解析式是 .
13.在直角坐标系中,抛物线与x轴交于点A,B(点A在点B的左侧),与y轴交于点C。如果点M在y轴的右侧的抛物线上,,那么点M的坐标为
14.请你选择你喜欢的a、b、c值,使二次函数y=ax2+bx+c(a≠0)的图象同时满足下列条件:
①开口方向向下;②当x<2时,y随x的增大而增大;当x>2时,y随x的增大而减小.这样的二次函数的解析式可以为 .
15.已知:抛物线与y轴交于C点,顶点为M,直线CM的解析式为 并且线段CM的长为,则抛物线的解析式为__________________________.
16.将抛物线的图象向上平移3个单位,则平移后的抛物线C1的解析式为 ,再将C1以原点为中心,旋转180度所得抛物线C2的解析式为_________________
三、计算题
17.(本小题满分12分)
如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA=16 cm, OC=8cm,现有两动点P、Q分别从O、C同时出发,P在线段OA上沿OA方向以每秒2 cm的速度匀速运动,Q在线段CO上沿CO方向以每秒1 cm的速度匀速运动.设运动时间为t秒.
(1)用含t的式子表示△OPQ的面积S;
(2)判断四边形OPBQ的面积是否是一个定值,如果是,请求出这个定值;如果不是,请说明理由;
(3)当△OPQ∽△ABP时,抛物线y=x2+bx+c经过B、P两点,求抛物线的解析式;
(4)在(3)的条件下,过线段BP上一动点M作轴的平
行线交抛物线于N,求线段MN的最大值.
如图,已知△ABC为直角三角形,∠ACB=90°,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的二次函数图像经过点B、D.
18.请直接写出用m表示点A、D的坐标
19.求这个二次函数的解析式;
20.点Q为二次函数图像上点P至点B之间的一点,连结PQ、BQ,求四边形ABQP面积的最大值.
四、解答题
21.已知:直角坐标平面内有点,过原点的直线,且与过点、的抛物线相交于第一象限的点,若.
(1)求抛物线的解析式;
(2)作轴于点,设有直线交直线于,交抛物线于点,若、、、组成的四边形是平行四边形,求的值。
22.已知二次函数y=x2+2x+m的图象C1与x轴有且只有一个公共点.
(1)求C1的顶点坐标;
(2)将C1向下平移若干个单位后,得抛物线C2,如果C2与x轴的一个交点为A(﹣3,0),求C2的函数关系式,并求C2与x轴的另一个交点坐标;
23.规律是数学研究的重要内容之一.
初中数学中研究的规律主要有一些特定的规则、符号(数)及其运算规律、图形的数值特征和位置关系特征等方面.请你解决以下与数的表示和运算相关的问题:
(1)写出奇数a用整数n表示的式子;
(2)写出有理数b用整数m和整数n表示的式子;
(3)函数的研究中,应关注y随x变化而变化的数值规律(课本里研究函数图象的特征实际上也是为了说明函数的数值规律).
下面对函数的某种数值变化规律进行初步研究:
0
1
2
3
4
5
...
0
1[
4
9
16
25
...
1
3
5
7
9
11
...
由表看出,当x的取值从0开始每增加1个单位时,y的值依次增加1,3,5...
请回答:
①当x的取值从0开始每增加个单位时,y的值变化规律是什么?
②当x的取值从0开始每增加个单位时,y的值变化规律是什么?
24.如图所示,在平面直角坐标系xOy中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.
(1)求抛物线的解析式.
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动,同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
①移动开始后第t秒时,设△PBQ的面积为S,试写出S与t之间的函数关系式,并写出t的取值范围.
②当S取得最大值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
25.我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形,不妨简称为“锅线”,锅口直径为6dm,锅深3dm,锅盖高1dm(锅口直径与锅盖直径视为相同),建立直接坐标系如图①所示,如果把锅纵断面的抛物线的记为C1,把锅盖纵断面的抛物线记为C2.
(1)求C1和C2的解析式;
(2)如图②,过点B作直线BE:y=x﹣1交C1于点E(﹣2,﹣),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;
(3)如果(2)中的直线BE保持不变,抛物线C1或C2上是否存在一点Q,使得△EBQ的面积最大?若存在,求出Q的坐标和△EBQ面积的最大值;若不存在,请说明理由.
26. 某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。 求:(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?(2)每件衬衫降价多少元时,商场平均每天赢利最多?
27.如图,在平面直角坐标系xOy中,四边形ABCD是菱形,顶点A.C.D均在坐标轴上,且AB=5,sinB=.
(1)求过A.C. D三点的抛物线的解析式;
(2)记直线AB的解析式为y1=mx+n,(1)中抛物线的解析式为y2=ax2+bx+c,求当y1<y2时,自变量x的取值范围;
(3)设直线AB与(1)中抛物线的另一个交点为E,P点为抛物线上A.E两点之间的一个动点,当P点在何处时,△PAE的面积最大?并求出面积的最大值.
参考答案
1.A
2.C
3.C
4.B
5.B
6.B
7.A
8. C
9. B
10. D
11.如:等,写出一个即可
12.
13.(4,6)或(1,-6)
14.
15.或
14.
17.
∴当m=-=10时,MN有最大值是9 …………………12分
18.A(3-m,0),D(0,m-3 )
19.设以P(1,0)为顶点的抛物线的解析式为y=a(x-1)2(a≠0)
∵抛物线过点B、D,
∴ 解得 …………4分
所以二次函数的解析式为y=(x-1)2,
即:y=x2-2x+1 …………5分
20.设点Q的坐标为(x,x2-2 x+1),显然1<x<3 …6分
连结BP,过点Q作QH⊥x轴,交BP于点H.
∵A(-1,0),P(1,0),B(3,4)
∴AP=2,BC=3,PC=2
由P(1,0),B(3,4)求得直线BP的解析式为y=2x-2
∵QH⊥x轴,点Q的坐标为(x,x2-2 x+1)
∴点H的横坐标为x,∴点H的坐标为(x,2x-2)
∴QH=2x-2-(x2-2x+1)=-x2+4x-3 …………7分
∴四边形ABQP面积S=S△APB+S△QPB=×AP×BC+×QH×PC
=×2×4+×(-x2+4x-3)×2
=-x2+4x+1=-(x-2)2+5 …………9分
∵1<x<3
∴当x=2时,S取得最大值为5, …………10分
即当点Q的坐标为(2,1)时,四边形ABQP面积的最大值为5
21.(1)解:过点A作AH⊥x轴于点H,过点B作BC⊥x轴于点C,
由点A(-1,2)可得 AH=2,OH=1
由直线OB⊥OA,可得△AHO∽△OCB,
∴ ,
∵OB=2OA,∴OC=4,BC=2 ,∴B(4,2)
设经过点A、O、B的抛物线解析式为
∴ )
解得, ∴抛物线解析式为:
(2)设直线l的解析式为
∵ 直线l经过点B(4,2), ∴ 直线l的解析式为
∵ 直线x=m(m>0)交直线l于,交抛物线于点Q,
∴ 设P点坐标为(m,m),点Q坐标为(m,),
∵由B、C、P、Q四点组成的四边形是平行四边形,∴ PQ//BC且PQ=BC
即: ,
解得或, ∵ m>0 ∴或2
22.解:(1)y=x2+2x+m=(x+1)2+m﹣1,对称轴为x=﹣1,
∵与x轴有且只有一个公共点,
∴顶点的纵坐标为0,
∴C1的顶点坐标为(﹣1,0);
(2)设C2的函数关系式为y=(x+1)2+k,
把A(﹣3,0)代入上式得(﹣3+1)2+k=0,得k=﹣4,
∴C2的函数关系式为y=(x+1)2﹣4.
∵抛物线的对称轴为x=﹣1,与x轴的一个交点为A(﹣3,0),
由对称性可知,它与x轴的另一个交点坐标为(1,0)
23.(1)2n+1(2)b=m/n (n≠0)(3) ①值依次增加、、·····②依次增加、、·····
24.(1)(2)①S=(t-3)2+9(0<t<6)②点R坐标为(3,﹣18)
25.(1)y=x2﹣3(﹣3≤x≤3),y=﹣x2+1(﹣3≤x≤3)(2)P1(,0)、P2(﹣,0)(3)(),
26.(1)20元(2)15元
27.解:(1)∵四边形ABCD是菱形,
∴AB=AD=CD=BC=5,sinB=sinD=;
Rt△OCD中,OC=CD?sinD=4,OD=3;
OA=AD﹣OD=2,即:
A(﹣2,0)、B(﹣5,4)、C(0,4)、D(3,0);
设抛物线的解析式为:y=a(x+2)(x﹣3),得:
2×(﹣3)a=4,a=﹣;
∴抛物线:y=﹣x2+x+4.
(2)由A(﹣2,0)、B(﹣5,4)得直线AB:y1=﹣x﹣;
由(1)得:y2=﹣x2+x+4,则:
,解得:,;
由图可知:当y1<y2时,﹣2<x<5.
(3)∵S△APE=AE?h,
∴当P到直线AB的距离最远时,S△ABC最大;
若设直线L∥AB,则直线L与抛物线有且只有一个交点时,该交点为点P;
设直线L:y=﹣x+b,当直线L与抛物线有且只有一个交点时,
﹣x+b=﹣x2+x+4,且△=0;
求得:b=,即直线L:y=﹣x+;
可得点P(,).
由(2)得:E(5,﹣),则直线PE:y=﹣x+9;
则点F(,0),AF=OA+OF=;
∴△PAE的最大值:S△PAE=S△PAF+S△AEF=××(+)=.
综上所述,当P(,)时,△PAE的面积最大,为.
