九年级上册数学第二十六章二次函数单元测试四(附答案)
文档属性
| 名称 | 九年级上册数学第二十六章二次函数单元测试四(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 533.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-17 15:47:47 | ||
图片预览


文档简介
九年级上册数学第二十六章二次函数单元测试四(附答案)
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.抛物线的顶点坐标是( ).
A.(1,0) B.(-1,0) C.(-2,1) D.(2,-1)
2.对于每个非零自然数,抛物线与x轴交于An、Bn两点,以表示这两点间的距离,则的值是( ).
A. B. C. D.
3.抛物线的对称轴为( ).
A.直线 B.直线 C.直线 D.直线
4.函数y=ax-2(a≠0)与y=ax2(a≠0)在同一平面坐标系中的图象可能是( )
5.已知函数的图象与轴有交点,则的取值范围是( ).
A.<4 B.≤4 C.<4且≠3 D.≤4且≠3
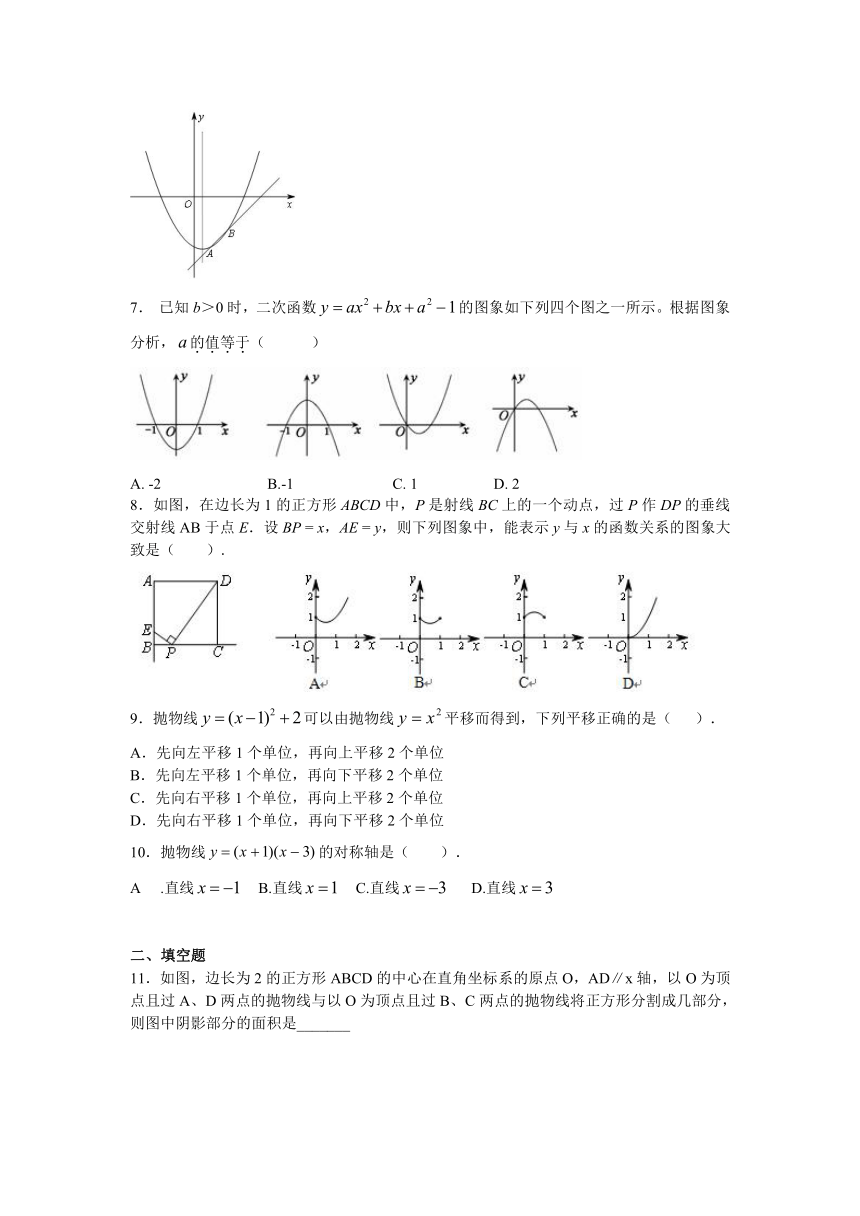
6.如图,抛物线y=x 2-x-与直线y=x-2交于A、B两点(点A在点B的左侧),动点P从A点出发,先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到点B.若使点P运动的总路径最短,则点P运动的总路径的长为( ).
A. B. C. D.
7. 已知b>0时,二次函数的图象如下列四个图之一所示。根据图象分析,的值等于( )
A. -2 B.-1 C. 1 D. 2
8.如图,在边长为1的正方形ABCD中,P是射线BC上的一个动点,过P作DP的垂线交射线AB于点E.设BP = x,AE = y,则下列图象中,能表示y与x的函数关系的图象大致是( ).
9.抛物线可以由抛物线平移而得到,下列平移正确的是( ).
A.先向左平移1个单位,再向上平移2个单位
B.先向左平移1个单位,再向下平移2个单位
C.先向右平移1个单位,再向上平移2个单位
D.先向右平移1个单位,再向下平移2个单位
10.抛物线的对称轴是( ).
A .直线 B.直线 C.直线 D.直线
二、填空题
11.如图,边长为2的正方形ABCD的中心在直角坐标系的原点O,AD∥x轴,以O为顶点且过A、D两点的抛物线与以O为顶点且过B、C两点的抛物线将正方形分割成几部分,则图中阴影部分的面积是_______
12.已知函数y=(m+2)xm(m+1)是二次函数,则m=______________。
13.函数y=-x2+2的图象的顶点坐标是 .
14.如果先将抛物线向左平移3个单位,再向下平移1个单位,那么所得到的抛物线的表达式为__________.
15.已知抛物线,则该抛物线的顶点坐标是 .
16.小明从二次函数y=ax2+bx+c的图象(如图)中观察
得出了下面五条信息:①c<0;②abc>0;③a-b+c>0;④2a-3b=0;⑤c-4b>0.
你认为其中正确的信息是_________________.(只填序号)
三、计算题
如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米. 现以O点为原点,OM所在直线为x轴建立直角坐标系.
17.直接写出点M及抛物线顶点P的坐标;
18.求这条抛物线的解析式;
19.若要搭建一个矩形“支撑架”AD- DC- CB,
使C、D点在抛物线上,A、B点在地面OM上,
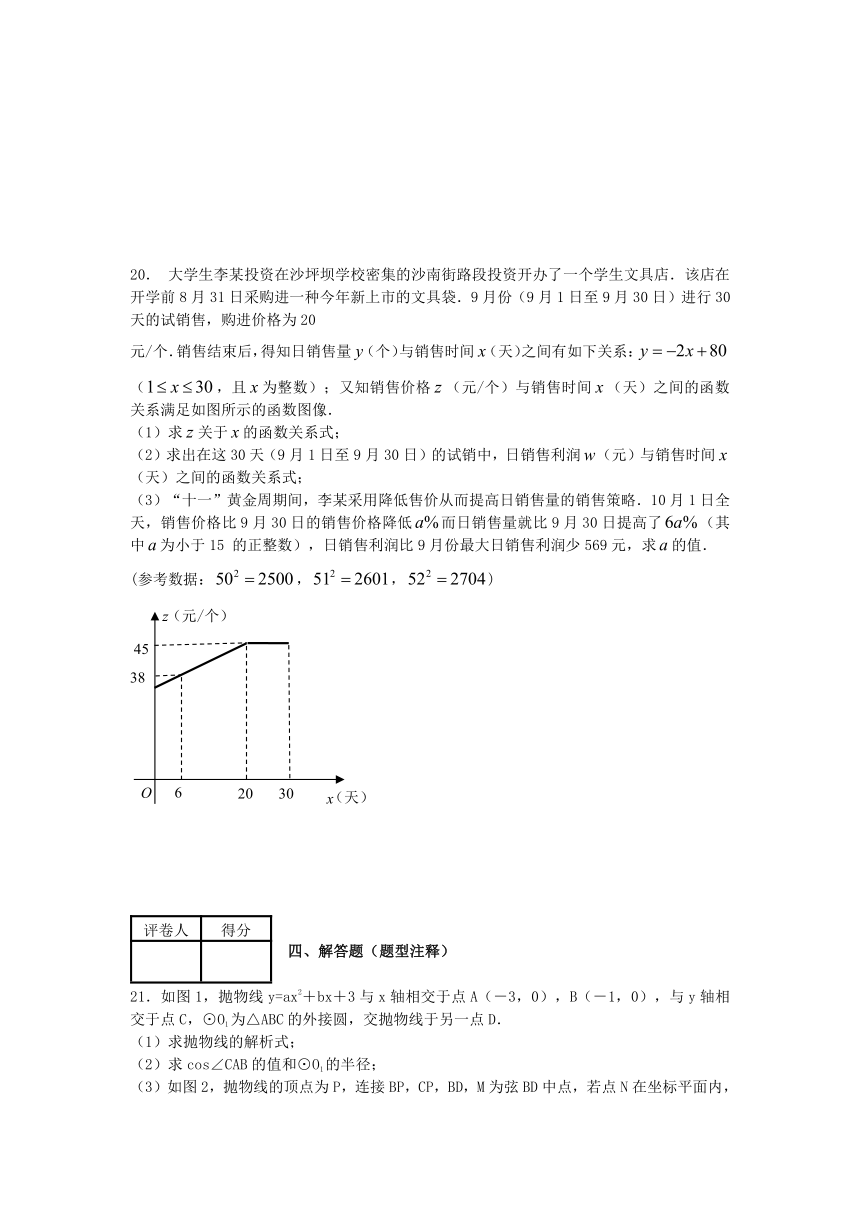
20. 大学生李某投资在沙坪坝学校密集的沙南街路段投资开办了一个学生文具店.该店在开学前8月31日采购进一种今年新上市的文具袋.9月份(9月1日至9月30日)进行30天的试销售,购进价格为20
元/个.销售结束后,得知日销售量(个)与销售时间(天)之间有如下关系:(,且为整数);又知销售价格(元/个)与销售时间(天)之间的函数关系满足如图所示的函数图像.
(1)求关于的函数关系式;
(2)求出在这30天(9月1日至9月30日)的试销中,日销售利润(元)与销售时间(天)之间的函数关系式;
(3)“十一”黄金周期间,李某采用降低售价从而提高日销售量的销售策略.10月1日全天,销售价格比9月30日的销售价格降低而日销售量就比9月30日提高了(其中为小于15 的正整数),日销售利润比9月份最大日销售利润少569元,求的值.
(参考数据:,,)
评卷人 得分
四、解答题(题型注释)
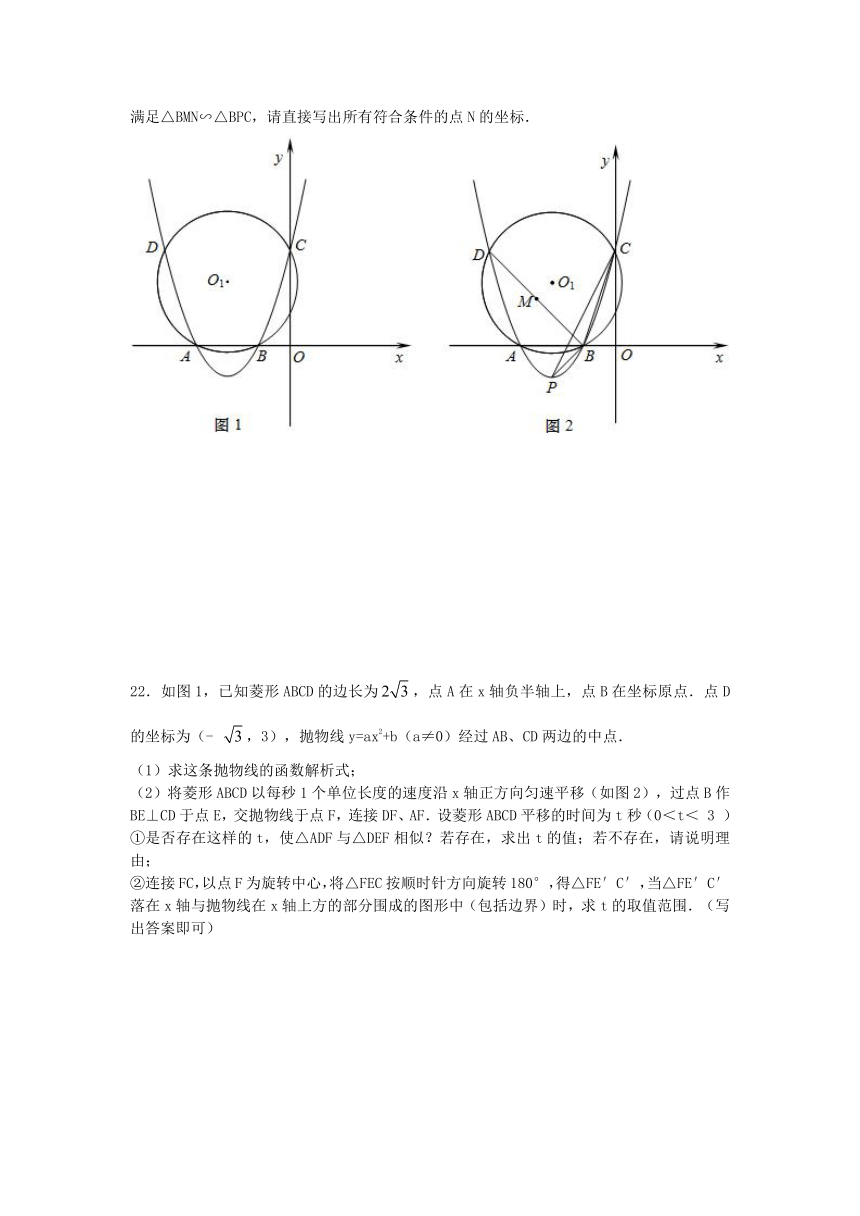
21.如图1,抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1为△ABC的外接圆,交抛物线于另一点D.
(1)求抛物线的解析式;
(2)求cos∠CAB的值和⊙O1的半径;
(3)如图2,抛物线的顶点为P,连接BP,CP,BD,M为弦BD中点,若点N在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点N的坐标.
22.如图1,已知菱形ABCD的边长为,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(- ,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
(1)求这条抛物线的函数解析式;
(2)将菱形ABCD以每秒1个单位长度的速度沿x轴正方向匀速平移(如图2),过点B作BE⊥CD于点E,交抛物线于点F,连接DF、AF.设菱形ABCD平移的时间为t秒(0<t< 3 )
①是否存在这样的t,使△ADF与△DEF相似?若存在,求出t的值;若不存在,请说明理由;
②连接FC,以点F为旋转中心,将△FEC按顺时针方向旋转180°,得△FE′C′,当△FE′C′落在x轴与抛物线在x轴上方的部分围成的图形中(包括边界)时,求t的取值范围.(写出答案即可)
23.二次函数y=﹣x2+2x+m的图象与x轴交于A.B两点(B在A右侧),顶点为C,且A.B两点间的距离等于点C到x轴的距离的2倍.
(1)求此抛物线的解析式.
(2)求直线BC的解析式.
(3)若点P在抛物线的对称轴上,且⊙P与x轴以及直线BC都相切,求点P的坐标.
【提示:(+1)(-1)=1】
24.如图,在平面直角坐标系中,矩形OABC四个顶点的坐标分别为O(0,0),A(0,3),B(6,3),C(6,0),抛物线过点A。
(1)(2分)求c的值; .
(2)(6分)若a=-l,且抛物线与矩形有且只有三个交点A、D、E,求△ADE的面积S的最大值;
(3)(6分)若抛物线与矩形有且只有三个交点A、M、N,线段MN的垂直平分线l过点O,交线段BC于点
F。当BF=1时,求抛物线的解析式.
25.如果一条抛物线与轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(1)“抛物线三角形”一定是 三角形;
(2)若抛物线的“抛物线三角形”是等腰直角三角形,求的值;
(3)如图,△是抛物线的“抛物线三角形”,是否存在以原点为对称中心的矩形?若存在,求出过三点的抛物线的表达式;若不存在,说明理由.
26. 如图,抛物线与轴交于A(-1,0),B(3,0) 两点.
(1) 求该抛物线的解析式;
(2) 设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标;
(3) 设(1)中抛物线交y 轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
27.如图,在△ABC中,AB=2,AC=BC= 5 .
(1)以AB所在的直线为x轴,AB的垂直平分线为y轴,建立直角坐标系如图,请你分别写出A、B、C三点的坐标;
(2)求过A、B、C三点且以C为顶点的抛物线的解析式;
(3)若D为抛物线上的一动点,当D点坐标为何值时,S△ABD=S△ABC;
(4)如果将(2)中的抛物线向右平移,且与x轴交于点A′B′,与y轴交于点C′,当平移多少个单位时,点C′同时在以A′B′为直径的圆上(解答过程如果有需要时,请参看阅读材料).
INCLUDEPICTURE "http://img..net/quiz/images/201207/29/71afea4f.png" \* MERGEFORMATINET INCLUDEPICTURE "http://img..net/quiz/images/201207/29/71afea4f.png" \* MERGEFORMATINET
附:阅读材料
一元二次方程常用的解法有配方法、公式法和因式分解法,对于一些特殊方程可以通过换元法转化为一元二次方程求解.如解方程:y4-4y2+3=0.
解:令y2=x(x≥0),则原方程变为x2-4x+3=0,解得x1=1,x2=3.
当x1=1时,即y2=1,∴y1=1,y2=-1.
当x2=3,即y2=3,∴y3= 3 ,y4=- 3 .
所以,原方程的解是y1=1,y2=-1,y3= 3 ,y4=- 3 .
再如 ,可设 ,用同样的方法也可求解.
参考答案
1.A
2.D
3.B
4.A
5.B
6.A
7.B
8. A
9. C
10.B
11.2
12.1
13.
14.
15.(1,3)
16. ①②③⑤
17.M(12,0),P(6,6).
18.设抛物线解析式为:. 3分
∵抛物线经过点(0,0),
∴,即 4分
∴抛物线解析式为:
.
19.设A(m,0),则
B(12-m,0),,. 7分
∴“支撑架”总长AD+DC+CB =
=. 10分
∵ 此二次函数的图象开口向下.
∴ 当m = 3米时,AD+DC+CB有最大值为15米.
20.25.(1)由图像知,当1≤x≤20时,设z=kx+b则有
当20<x≤30时z=45
(2)当1≤x≤20时,
=-x2+10x+1200
当20<x≤30时,
W=yz-20y=45(-2x+80)-20(-2x+80)
=-50x+2000
(3)9月30日的价格为45元,日销售量为20个
9月份当1≤x≤20时日销售利润为
W=-x2+10x+1200=-(x2-10x+25)+1225=-(x-5)2+1225
当9月5日时日利润最大为1225元.
当20<x≤30时,利润为W=-50x+2000,
当x增加时W减小,故为x=21时最大.最大日销售利润为950元
综上9月份日销售利润最大为1225元.
由题意得45(1-a%)·20(1+6a%)-20×20(1+6a%)=1225-569
化简得18a2-700a+5200=0
a1=10,
答:a的值为10.
21.(1)y=x2+4x+3(2),(3)(,)或(,)
22.(1)y=-x2+3(2)①存在,t=1②
23.(1)y=﹣x2+2x
(2)y=﹣x+2
(3)解:设点P(1,n),过点P作PD⊥BC,则PC=n,∴1-n=n,∴n=-1,∴点P(1,-1).
24.(1)3(2) (3) 或
25.(1)等腰(2)(3)存在,
26.(1) y=x2-2x-3(2) 当P点的坐标分别为、、(1,-4)时,S△PAB=8. (3) 点Q的坐标为(1,-2)
27.解:(1)∵AB的垂直平分线为y轴,
∴OA=OB=AB=×2=1,
∴A的坐标是(-1,0),B的坐标是(1,0).
在直角△OAC中,,
则C的坐标是:(0,2);
(2)设抛物线的解析式是:y=ax2+b,
根据题意得: ,解得: ,
则抛物线的解析式是:;
(3)∵S△ABC=AB OC=×2×2=2,
∴S△ABD=S△ABC=1.
设D的纵坐标是m,则AB |m|=1,
则m=±1.
当m=1时,-2x2+2=1,解得:x=±,
当m=-1时,,-2x2+2=-1,解得:x=± ,
则D的坐标是:(,1)或(- ,1)或(,-1),或(- ,-1).
(4)设抛物线向右平移c个单位长度,则0<c≤1,OA′=1-c,OB′=1+c.
平移以后的抛物线的解析式是:y=-2(x-c)2+b.
令x=0,解得y=-2c2+2.即OC′= -2c2+2.
当点C′同时在以A′B′为直径的圆上时有:OC′2=OA′ OB′,
则(-2c2+2)2=(1-c)(1+c),
即(4c2-3)(c2-1)=0,
解得:c= ,(舍去),1,(舍去).
故平移 或1个单位长度.
45
38
20
30
x
(天)
(元/个)
z
O
6
试卷第2页,总6页
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.抛物线的顶点坐标是( ).
A.(1,0) B.(-1,0) C.(-2,1) D.(2,-1)
2.对于每个非零自然数,抛物线与x轴交于An、Bn两点,以表示这两点间的距离,则的值是( ).
A. B. C. D.
3.抛物线的对称轴为( ).
A.直线 B.直线 C.直线 D.直线
4.函数y=ax-2(a≠0)与y=ax2(a≠0)在同一平面坐标系中的图象可能是( )
5.已知函数的图象与轴有交点,则的取值范围是( ).
A.<4 B.≤4 C.<4且≠3 D.≤4且≠3
6.如图,抛物线y=x 2-x-与直线y=x-2交于A、B两点(点A在点B的左侧),动点P从A点出发,先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到点B.若使点P运动的总路径最短,则点P运动的总路径的长为( ).
A. B. C. D.
7. 已知b>0时,二次函数的图象如下列四个图之一所示。根据图象分析,的值等于( )
A. -2 B.-1 C. 1 D. 2
8.如图,在边长为1的正方形ABCD中,P是射线BC上的一个动点,过P作DP的垂线交射线AB于点E.设BP = x,AE = y,则下列图象中,能表示y与x的函数关系的图象大致是( ).
9.抛物线可以由抛物线平移而得到,下列平移正确的是( ).
A.先向左平移1个单位,再向上平移2个单位
B.先向左平移1个单位,再向下平移2个单位
C.先向右平移1个单位,再向上平移2个单位
D.先向右平移1个单位,再向下平移2个单位
10.抛物线的对称轴是( ).
A .直线 B.直线 C.直线 D.直线
二、填空题
11.如图,边长为2的正方形ABCD的中心在直角坐标系的原点O,AD∥x轴,以O为顶点且过A、D两点的抛物线与以O为顶点且过B、C两点的抛物线将正方形分割成几部分,则图中阴影部分的面积是_______
12.已知函数y=(m+2)xm(m+1)是二次函数,则m=______________。
13.函数y=-x2+2的图象的顶点坐标是 .
14.如果先将抛物线向左平移3个单位,再向下平移1个单位,那么所得到的抛物线的表达式为__________.
15.已知抛物线,则该抛物线的顶点坐标是 .
16.小明从二次函数y=ax2+bx+c的图象(如图)中观察
得出了下面五条信息:①c<0;②abc>0;③a-b+c>0;④2a-3b=0;⑤c-4b>0.
你认为其中正确的信息是_________________.(只填序号)
三、计算题
如图,某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米. 现以O点为原点,OM所在直线为x轴建立直角坐标系.
17.直接写出点M及抛物线顶点P的坐标;
18.求这条抛物线的解析式;
19.若要搭建一个矩形“支撑架”AD- DC- CB,
使C、D点在抛物线上,A、B点在地面OM上,
20. 大学生李某投资在沙坪坝学校密集的沙南街路段投资开办了一个学生文具店.该店在开学前8月31日采购进一种今年新上市的文具袋.9月份(9月1日至9月30日)进行30天的试销售,购进价格为20
元/个.销售结束后,得知日销售量(个)与销售时间(天)之间有如下关系:(,且为整数);又知销售价格(元/个)与销售时间(天)之间的函数关系满足如图所示的函数图像.
(1)求关于的函数关系式;
(2)求出在这30天(9月1日至9月30日)的试销中,日销售利润(元)与销售时间(天)之间的函数关系式;
(3)“十一”黄金周期间,李某采用降低售价从而提高日销售量的销售策略.10月1日全天,销售价格比9月30日的销售价格降低而日销售量就比9月30日提高了(其中为小于15 的正整数),日销售利润比9月份最大日销售利润少569元,求的值.
(参考数据:,,)
评卷人 得分
四、解答题(题型注释)
21.如图1,抛物线y=ax2+bx+3与x轴相交于点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1为△ABC的外接圆,交抛物线于另一点D.
(1)求抛物线的解析式;
(2)求cos∠CAB的值和⊙O1的半径;
(3)如图2,抛物线的顶点为P,连接BP,CP,BD,M为弦BD中点,若点N在坐标平面内,满足△BMN∽△BPC,请直接写出所有符合条件的点N的坐标.
22.如图1,已知菱形ABCD的边长为,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(- ,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
(1)求这条抛物线的函数解析式;
(2)将菱形ABCD以每秒1个单位长度的速度沿x轴正方向匀速平移(如图2),过点B作BE⊥CD于点E,交抛物线于点F,连接DF、AF.设菱形ABCD平移的时间为t秒(0<t< 3 )
①是否存在这样的t,使△ADF与△DEF相似?若存在,求出t的值;若不存在,请说明理由;
②连接FC,以点F为旋转中心,将△FEC按顺时针方向旋转180°,得△FE′C′,当△FE′C′落在x轴与抛物线在x轴上方的部分围成的图形中(包括边界)时,求t的取值范围.(写出答案即可)
23.二次函数y=﹣x2+2x+m的图象与x轴交于A.B两点(B在A右侧),顶点为C,且A.B两点间的距离等于点C到x轴的距离的2倍.
(1)求此抛物线的解析式.
(2)求直线BC的解析式.
(3)若点P在抛物线的对称轴上,且⊙P与x轴以及直线BC都相切,求点P的坐标.
【提示:(+1)(-1)=1】
24.如图,在平面直角坐标系中,矩形OABC四个顶点的坐标分别为O(0,0),A(0,3),B(6,3),C(6,0),抛物线过点A。
(1)(2分)求c的值; .
(2)(6分)若a=-l,且抛物线与矩形有且只有三个交点A、D、E,求△ADE的面积S的最大值;
(3)(6分)若抛物线与矩形有且只有三个交点A、M、N,线段MN的垂直平分线l过点O,交线段BC于点
F。当BF=1时,求抛物线的解析式.
25.如果一条抛物线与轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(1)“抛物线三角形”一定是 三角形;
(2)若抛物线的“抛物线三角形”是等腰直角三角形,求的值;
(3)如图,△是抛物线的“抛物线三角形”,是否存在以原点为对称中心的矩形?若存在,求出过三点的抛物线的表达式;若不存在,说明理由.
26. 如图,抛物线与轴交于A(-1,0),B(3,0) 两点.
(1) 求该抛物线的解析式;
(2) 设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标;
(3) 设(1)中抛物线交y 轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
27.如图,在△ABC中,AB=2,AC=BC= 5 .
(1)以AB所在的直线为x轴,AB的垂直平分线为y轴,建立直角坐标系如图,请你分别写出A、B、C三点的坐标;
(2)求过A、B、C三点且以C为顶点的抛物线的解析式;
(3)若D为抛物线上的一动点,当D点坐标为何值时,S△ABD=S△ABC;
(4)如果将(2)中的抛物线向右平移,且与x轴交于点A′B′,与y轴交于点C′,当平移多少个单位时,点C′同时在以A′B′为直径的圆上(解答过程如果有需要时,请参看阅读材料).
INCLUDEPICTURE "http://img..net/quiz/images/201207/29/71afea4f.png" \* MERGEFORMATINET INCLUDEPICTURE "http://img..net/quiz/images/201207/29/71afea4f.png" \* MERGEFORMATINET
附:阅读材料
一元二次方程常用的解法有配方法、公式法和因式分解法,对于一些特殊方程可以通过换元法转化为一元二次方程求解.如解方程:y4-4y2+3=0.
解:令y2=x(x≥0),则原方程变为x2-4x+3=0,解得x1=1,x2=3.
当x1=1时,即y2=1,∴y1=1,y2=-1.
当x2=3,即y2=3,∴y3= 3 ,y4=- 3 .
所以,原方程的解是y1=1,y2=-1,y3= 3 ,y4=- 3 .
再如 ,可设 ,用同样的方法也可求解.
参考答案
1.A
2.D
3.B
4.A
5.B
6.A
7.B
8. A
9. C
10.B
11.2
12.1
13.
14.
15.(1,3)
16. ①②③⑤
17.M(12,0),P(6,6).
18.设抛物线解析式为:. 3分
∵抛物线经过点(0,0),
∴,即 4分
∴抛物线解析式为:
.
19.设A(m,0),则
B(12-m,0),,. 7分
∴“支撑架”总长AD+DC+CB =
=. 10分
∵ 此二次函数的图象开口向下.
∴ 当m = 3米时,AD+DC+CB有最大值为15米.
20.25.(1)由图像知,当1≤x≤20时,设z=kx+b则有
当20<x≤30时z=45
(2)当1≤x≤20时,
=-x2+10x+1200
当20<x≤30时,
W=yz-20y=45(-2x+80)-20(-2x+80)
=-50x+2000
(3)9月30日的价格为45元,日销售量为20个
9月份当1≤x≤20时日销售利润为
W=-x2+10x+1200=-(x2-10x+25)+1225=-(x-5)2+1225
当9月5日时日利润最大为1225元.
当20<x≤30时,利润为W=-50x+2000,
当x增加时W减小,故为x=21时最大.最大日销售利润为950元
综上9月份日销售利润最大为1225元.
由题意得45(1-a%)·20(1+6a%)-20×20(1+6a%)=1225-569
化简得18a2-700a+5200=0
a1=10,
答:a的值为10.
21.(1)y=x2+4x+3(2),(3)(,)或(,)
22.(1)y=-x2+3(2)①存在,t=1②
23.(1)y=﹣x2+2x
(2)y=﹣x+2
(3)解:设点P(1,n),过点P作PD⊥BC,则PC=n,∴1-n=n,∴n=-1,∴点P(1,-1).
24.(1)3(2) (3) 或
25.(1)等腰(2)(3)存在,
26.(1) y=x2-2x-3(2) 当P点的坐标分别为、、(1,-4)时,S△PAB=8. (3) 点Q的坐标为(1,-2)
27.解:(1)∵AB的垂直平分线为y轴,
∴OA=OB=AB=×2=1,
∴A的坐标是(-1,0),B的坐标是(1,0).
在直角△OAC中,,
则C的坐标是:(0,2);
(2)设抛物线的解析式是:y=ax2+b,
根据题意得: ,解得: ,
则抛物线的解析式是:;
(3)∵S△ABC=AB OC=×2×2=2,
∴S△ABD=S△ABC=1.
设D的纵坐标是m,则AB |m|=1,
则m=±1.
当m=1时,-2x2+2=1,解得:x=±,
当m=-1时,,-2x2+2=-1,解得:x=± ,
则D的坐标是:(,1)或(- ,1)或(,-1),或(- ,-1).
(4)设抛物线向右平移c个单位长度,则0<c≤1,OA′=1-c,OB′=1+c.
平移以后的抛物线的解析式是:y=-2(x-c)2+b.
令x=0,解得y=-2c2+2.即OC′= -2c2+2.
当点C′同时在以A′B′为直径的圆上时有:OC′2=OA′ OB′,
则(-2c2+2)2=(1-c)(1+c),
即(4c2-3)(c2-1)=0,
解得:c= ,(舍去),1,(舍去).
故平移 或1个单位长度.
45
38
20
30
x
(天)
(元/个)
z
O
6
试卷第2页,总6页
