北师大版八年级数学下册2.5一元一次不等式与一次函数 课件(共21张PPT)
文档属性
| 名称 | 北师大版八年级数学下册2.5一元一次不等式与一次函数 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 547.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-13 08:20:57 | ||
图片预览








文档简介
(共21张PPT)
5 一元一次不等式与一次函数
(第一课时)
版 本:北京师范大学出版社
章 节:八年级下册 第二章 一元一次不等式与一次函数(1)
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑,已知弟弟每秒跑3m,哥哥每秒跑4m.
(1)何时弟弟跑在哥哥前面
(2)何时哥哥跑在弟弟前面
所以,从哥哥起跑,9秒之前弟弟跑在哥哥前面,9秒之后哥哥跑在弟弟前面.
解:9÷(4-3)=9(秒)
情境引入
所以,从哥哥起跑,9秒之前弟弟跑在哥哥前面,9秒之后哥哥跑在弟弟前面.
解:设哥哥起跑x秒追上弟弟.
4x-3x=9
解得:x=9.
情境引入
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑,已知弟弟每秒跑3m,哥哥每秒跑4m.
(1)何时弟弟跑在哥哥前面
(2)何时哥哥跑在弟弟前面
所以,从哥哥起跑,9秒之前弟弟跑在哥哥前面,9秒之后哥哥跑在弟弟前面.
解:(1)设哥哥起跑x秒时弟弟在哥哥前面.
3x+9>4x
解得:x<9
情境引入
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑,已知弟弟每秒跑3m,哥哥每秒跑4m.
(1)何时弟弟跑在哥哥前面
(2)何时哥哥跑在弟弟前面
解:(2)设哥哥起跑y秒时哥哥在弟弟前面.
所以,从哥哥起跑,9秒之后哥哥跑在弟弟前面.
4y>3y+9
解得:y>9
情境引入
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑,已知弟弟每秒跑3m,哥哥每秒跑4m.
(1)何时弟弟跑在哥哥前面
(2)何时哥哥跑在弟弟前面
1.通过观察函数图象、求方程的解和不等式的解集,从中体会一元一次方程、一元一次不等式与一次函数的内在联系;
2.通过具体问题初步体会一次函数的变化规律与一元一次不等式解集的联系;
3.利用数形结合的思想,多角度解决一元一次不等式的问题,体会数学思想方法的应用.
学习目标
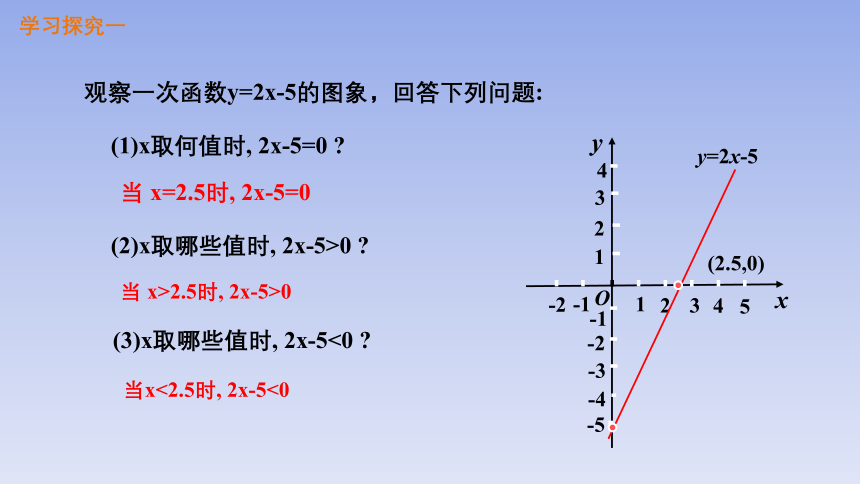
观察一次函数y=2x-5的图象,回答下列问题:
(1)x取何值时, 2x-5=0
(2.5,0)
O
1
2
3
4
5
-2
-1
x
2
3
1
4
-3
-5
-2
-4
y
-1
y=2x-5
(2)x取哪些值时, 2x-5>0
(3)x取哪些值时, 2x-5<0
当 x=2.5时, 2x-5=0
当 x>2.5时, 2x-5>0
当x<2.5时, 2x-5<0
学习探究一
(4)x取何值时, 2x-5=1
y=1
(3,1)
O
1
2
3
4
5
-2
-1
x
2
3
1
4
-3
-5
-2
-4
y
-1
y=2x-5
(5)x取哪些值时, 2x-5>1
(6)x取哪些值时,2x-5<1
观察一次函数y=2x-5的图象,回答下列问题:
当 x=3时, 2x-5=1
当 x>3时, 2x-5>1
当 x<3时, 2x-5<1
学习探究一
如果y=-2x-5,那么当x取哪些值时, y<0 当x取哪些值时,y<1?
思路二:
将函数问题转化为不等式问题.
思路一:
O
-3
-2
-1
1
2
-5
-4
x
2
-1
3
1
4
-3
-5
-2
-4
y
y=-2x-5
(-2.5,0)
作一次函数y=-2x-5的图象,直观观察.
-2x-5<0
-2x-5<1
x>-2.5
当x>-2.5时,y<0.
x>-3
当x>-3时,y<1.
想一想
求ax+b>c(或是常数,a≠0)的解集
函数y= ax+b的函数值
大于c(或小于c)时x
的取值范围
直线y= ax+b图象在直线
y=c上方(或下方),
横坐标的取值范围
从数的角度看
从形的角度看
求ax+b>c(或是常数,a≠0)的解集
概括总结
通过对函数图象的观察、分析,我们既可以运用函数图象解不等式,也可以运用解不等式帮助研究函数问题,二者相互渗透,互相作用. 不等式与函数是紧密联系着的一个整体.
概括总结
-2
x
y=3x+6
y
根据下列一次函数的图象,直接写出下列不等式的解集.
(1)3x+6>0
(2)3x+6<6
x>-2
x<0
6
巩固练习
因此,当x>3 时,y1>y2.
已知y1=2x-5, y2=-x+4,当x取何值时,y1>y2
解:根据题意,得
2x-5> -x+4,
解得x>3.
当x取何值时,y1O
1
2
3
4
5
-2
-1
x
2
3
1
4
-3
-5
-2
-4
y
-1
y1=2x-5
y2=-x+4
(3,1)
当x<3 时,y1学习探究二
求ax+b>mx+n(或
ax+by1>y2(或y1<y2)时自变量x
的取值范围
直线y1=ax+b图象在直线
y2=mx+n上方(或下方),
横坐标的取值范围
从数的角度看
从形的角度看
求ax+b>mx+n(或
ax+b一次函数y1=ax+b, y2=mx+n(a, b,m,n是常数,a≠0,m≠0)
概括总结
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑,已知弟弟每秒跑3m,哥哥每秒跑4m.
(1)何时弟弟跑在哥哥前面
(2)何时哥哥跑在弟弟前面
解:设哥哥起跑后所用的时间为x(s). 哥哥跑过的距离为y1(m),弟弟跑过的距离为y2(m).
y1=4x
y2=3x+9
问题解决
(1)_______________时,弟弟跑在哥哥前面.
(2)__________时,哥哥跑在弟弟前面.
(3)______先跑过20m,______先跑过100m.
思路一:图象法
0x>9
y1=4x
y2=3x+9
O
6
8
10
2
x(s)
4
12
24
12
30
18
36
6
y(m)
42
48
弟弟
哥哥
(9,36)
9
问题解决
思路二:代数法
哥哥: y1=4x
弟弟: y2=3x+9
(1)何时弟弟跑在哥哥前面
(2)何时哥哥跑在弟弟前面
由y1解得:x<9
所以,从哥哥起跑,9秒之前弟弟跑在哥哥前面.
由y1>y2得,4x>3x+9
解得:x>9
所以,从哥哥起跑,9秒之后哥哥跑在弟弟前面.
问题解决
(3)谁先跑过20m 谁先跑过100m
4x=20
3x+9=20
x=5
4x=100
3x+9=100
x=25
∴弟弟先跑过20m.
∴哥哥先跑过100m.
思路二:代数法
问题解决
1.利用y= 的图象,回答下列问题:
y
2
5
x
y=
x<2
x<0
当堂检测
2.如图1,某航空公司托运行李的费用与托运行李的重量的关系为一次函数,由图可知行李的重量只要不超过________千克,就可以免费托运.
3.如图2,l1反映了某产品的销售收入和销售量之间的关系,l2反映了该产品的销售成本与销售量之间的关系,当销售收入大于销售成本时,该产品才开始盈利. 该产品的销售量达到________吨时,生产该产品才能盈利?
图1
图2
20
4
当堂检测
必做题:课本P51, 习题 1、3
选做题:
甲、乙两家超市以相同的价格出售同样的商品.为了吸引顾客,各自推出不同的优惠方案.在甲超市累计购买商品超出 300 元之后,超出部分按原价八折优惠.在乙超市累计购买商品超出 200 元之后,超出部分按原价八五折优惠.设顾客预计累计购物 x元(x>300).
(1)请用含x的代数式分别表示顾客在两家超市购物所付的费用;
(2)试比较顾客到哪家超市购物更优惠?说明理由.
布置作业
5 一元一次不等式与一次函数
(第一课时)
版 本:北京师范大学出版社
章 节:八年级下册 第二章 一元一次不等式与一次函数(1)
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑,已知弟弟每秒跑3m,哥哥每秒跑4m.
(1)何时弟弟跑在哥哥前面
(2)何时哥哥跑在弟弟前面
所以,从哥哥起跑,9秒之前弟弟跑在哥哥前面,9秒之后哥哥跑在弟弟前面.
解:9÷(4-3)=9(秒)
情境引入
所以,从哥哥起跑,9秒之前弟弟跑在哥哥前面,9秒之后哥哥跑在弟弟前面.
解:设哥哥起跑x秒追上弟弟.
4x-3x=9
解得:x=9.
情境引入
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑,已知弟弟每秒跑3m,哥哥每秒跑4m.
(1)何时弟弟跑在哥哥前面
(2)何时哥哥跑在弟弟前面
所以,从哥哥起跑,9秒之前弟弟跑在哥哥前面,9秒之后哥哥跑在弟弟前面.
解:(1)设哥哥起跑x秒时弟弟在哥哥前面.
3x+9>4x
解得:x<9
情境引入
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑,已知弟弟每秒跑3m,哥哥每秒跑4m.
(1)何时弟弟跑在哥哥前面
(2)何时哥哥跑在弟弟前面
解:(2)设哥哥起跑y秒时哥哥在弟弟前面.
所以,从哥哥起跑,9秒之后哥哥跑在弟弟前面.
4y>3y+9
解得:y>9
情境引入
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑,已知弟弟每秒跑3m,哥哥每秒跑4m.
(1)何时弟弟跑在哥哥前面
(2)何时哥哥跑在弟弟前面
1.通过观察函数图象、求方程的解和不等式的解集,从中体会一元一次方程、一元一次不等式与一次函数的内在联系;
2.通过具体问题初步体会一次函数的变化规律与一元一次不等式解集的联系;
3.利用数形结合的思想,多角度解决一元一次不等式的问题,体会数学思想方法的应用.
学习目标
观察一次函数y=2x-5的图象,回答下列问题:
(1)x取何值时, 2x-5=0
(2.5,0)
O
1
2
3
4
5
-2
-1
x
2
3
1
4
-3
-5
-2
-4
y
-1
y=2x-5
(2)x取哪些值时, 2x-5>0
(3)x取哪些值时, 2x-5<0
当 x=2.5时, 2x-5=0
当 x>2.5时, 2x-5>0
当x<2.5时, 2x-5<0
学习探究一
(4)x取何值时, 2x-5=1
y=1
(3,1)
O
1
2
3
4
5
-2
-1
x
2
3
1
4
-3
-5
-2
-4
y
-1
y=2x-5
(5)x取哪些值时, 2x-5>1
(6)x取哪些值时,2x-5<1
观察一次函数y=2x-5的图象,回答下列问题:
当 x=3时, 2x-5=1
当 x>3时, 2x-5>1
当 x<3时, 2x-5<1
学习探究一
如果y=-2x-5,那么当x取哪些值时, y<0 当x取哪些值时,y<1?
思路二:
将函数问题转化为不等式问题.
思路一:
O
-3
-2
-1
1
2
-5
-4
x
2
-1
3
1
4
-3
-5
-2
-4
y
y=-2x-5
(-2.5,0)
作一次函数y=-2x-5的图象,直观观察.
-2x-5<0
-2x-5<1
x>-2.5
当x>-2.5时,y<0.
x>-3
当x>-3时,y<1.
想一想
求ax+b>c(或
函数y= ax+b的函数值
大于c(或小于c)时x
的取值范围
直线y= ax+b图象在直线
y=c上方(或下方),
横坐标的取值范围
从数的角度看
从形的角度看
求ax+b>c(或
概括总结
通过对函数图象的观察、分析,我们既可以运用函数图象解不等式,也可以运用解不等式帮助研究函数问题,二者相互渗透,互相作用. 不等式与函数是紧密联系着的一个整体.
概括总结
-2
x
y=3x+6
y
根据下列一次函数的图象,直接写出下列不等式的解集.
(1)3x+6>0
(2)3x+6<6
x>-2
x<0
6
巩固练习
因此,当x>3 时,y1>y2.
已知y1=2x-5, y2=-x+4,当x取何值时,y1>y2
解:根据题意,得
2x-5> -x+4,
解得x>3.
当x取何值时,y1
1
2
3
4
5
-2
-1
x
2
3
1
4
-3
-5
-2
-4
y
-1
y1=2x-5
y2=-x+4
(3,1)
当x<3 时,y1
求ax+b>mx+n(或
ax+b
的取值范围
直线y1=ax+b图象在直线
y2=mx+n上方(或下方),
横坐标的取值范围
从数的角度看
从形的角度看
求ax+b>mx+n(或
ax+b
概括总结
兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑,已知弟弟每秒跑3m,哥哥每秒跑4m.
(1)何时弟弟跑在哥哥前面
(2)何时哥哥跑在弟弟前面
解:设哥哥起跑后所用的时间为x(s). 哥哥跑过的距离为y1(m),弟弟跑过的距离为y2(m).
y1=4x
y2=3x+9
问题解决
(1)_______________时,弟弟跑在哥哥前面.
(2)__________时,哥哥跑在弟弟前面.
(3)______先跑过20m,______先跑过100m.
思路一:图象法
0
y1=4x
y2=3x+9
O
6
8
10
2
x(s)
4
12
24
12
30
18
36
6
y(m)
42
48
弟弟
哥哥
(9,36)
9
问题解决
思路二:代数法
哥哥: y1=4x
弟弟: y2=3x+9
(1)何时弟弟跑在哥哥前面
(2)何时哥哥跑在弟弟前面
由y1
所以,从哥哥起跑,9秒之前弟弟跑在哥哥前面.
由y1>y2得,4x>3x+9
解得:x>9
所以,从哥哥起跑,9秒之后哥哥跑在弟弟前面.
问题解决
(3)谁先跑过20m 谁先跑过100m
4x=20
3x+9=20
x=5
4x=100
3x+9=100
x=25
∴弟弟先跑过20m.
∴哥哥先跑过100m.
思路二:代数法
问题解决
1.利用y= 的图象,回答下列问题:
y
2
5
x
y=
x<2
x<0
当堂检测
2.如图1,某航空公司托运行李的费用与托运行李的重量的关系为一次函数,由图可知行李的重量只要不超过________千克,就可以免费托运.
3.如图2,l1反映了某产品的销售收入和销售量之间的关系,l2反映了该产品的销售成本与销售量之间的关系,当销售收入大于销售成本时,该产品才开始盈利. 该产品的销售量达到________吨时,生产该产品才能盈利?
图1
图2
20
4
当堂检测
必做题:课本P51, 习题 1、3
选做题:
甲、乙两家超市以相同的价格出售同样的商品.为了吸引顾客,各自推出不同的优惠方案.在甲超市累计购买商品超出 300 元之后,超出部分按原价八折优惠.在乙超市累计购买商品超出 200 元之后,超出部分按原价八五折优惠.设顾客预计累计购物 x元(x>300).
(1)请用含x的代数式分别表示顾客在两家超市购物所付的费用;
(2)试比较顾客到哪家超市购物更优惠?说明理由.
布置作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
