1.3.1 线段的垂直平分线 课件(共21张PPT)
文档属性
| 名称 | 1.3.1 线段的垂直平分线 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 18:23:57 | ||
图片预览




文档简介
(共21张PPT)
第一章 三角形的证明
3.1 线段的垂直平分线
学习目标
1.理解线段垂直平分线的概念;
2.掌握线段垂直平分线的性质定理及逆定理;(重点)
3.能运用线段的垂直平分线的有关知识进行证明或计算.(难点)
情境导入
为了方便居民的生活,政府计划在三个住宅小区A、B、C之间新建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等?
A
B
C
探究交流
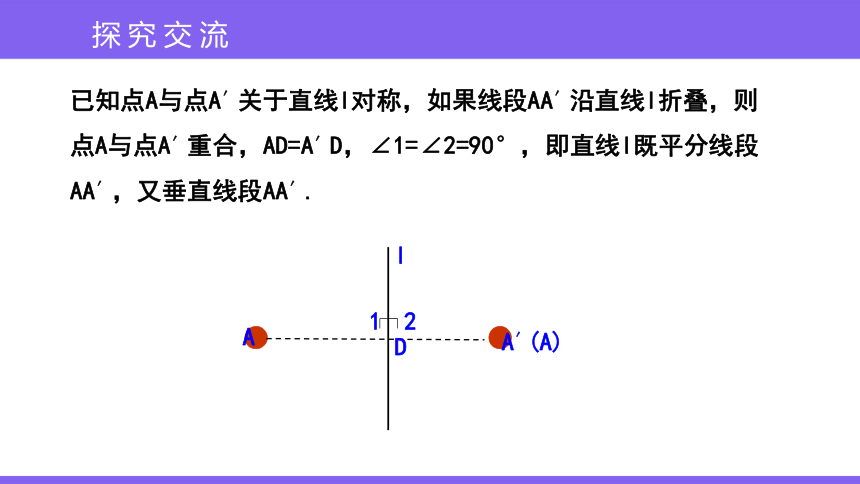
已知点A与点A′关于直线l对称,如果线段AA′沿直线l折叠,则点A与点A′重合,AD=A′D,∠1=∠2=90°,即直线l既平分线段AA′,又垂直线段AA′.
●
●
l
A
A′
D
2
1
(A)
我们把垂直且平分一条线段的直线叫作这条线段的垂直平分线.
由上可知:线段是轴对称图形,线段的垂直平分线是它的对称轴.
探究交流
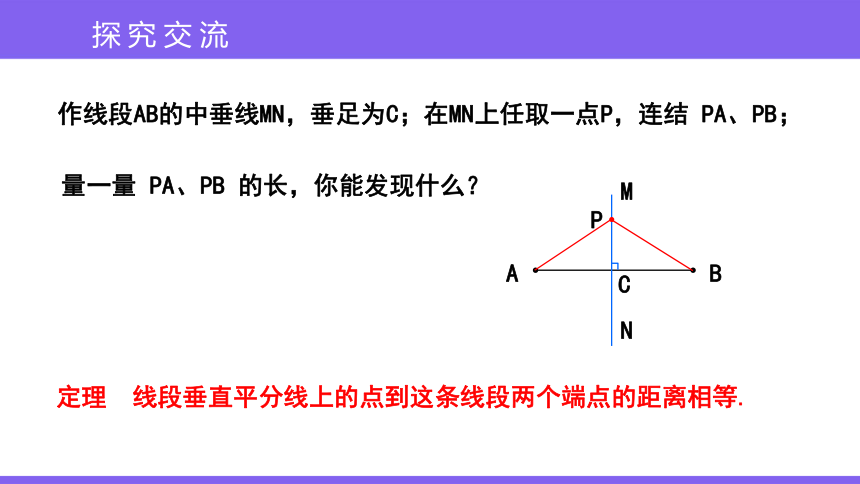
作线段AB的中垂线MN,垂足为C;在MN上任取一点P,连结 PA、PB;
量一量 PA、PB 的长,你能发现什么?
A
B
M
N
C
P
定理 线段垂直平分线上的点到这条线段两个端点的距离相等.
探究交流
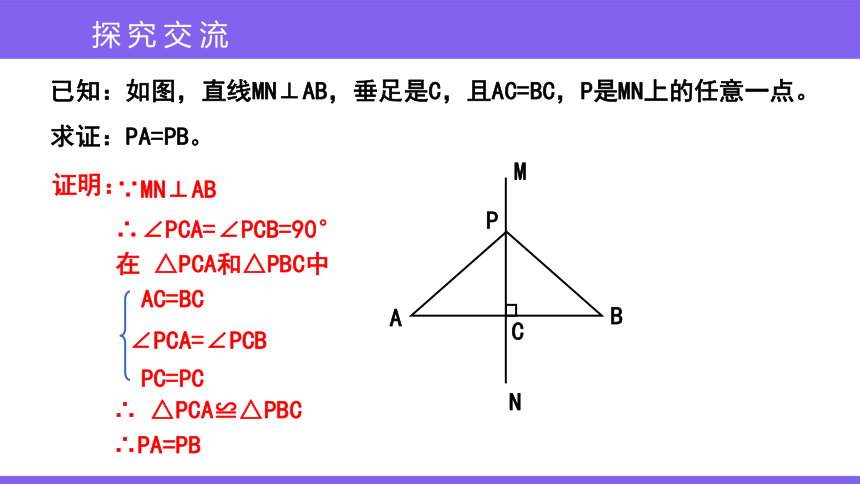
已知:如图,直线MN⊥AB,垂足是C,且AC=BC,P是MN上的任意一点。
求证:PA=PB。
证明:
∵MN⊥AB
∴∠PCA=∠PCB=90°
AC=BC
PC=PC
在 △PCA和△PBC中
∠PCA=∠PCB
∴ △PCA≌△PBC
∴PA=PB
N
M
B
A
P
C
探究交流
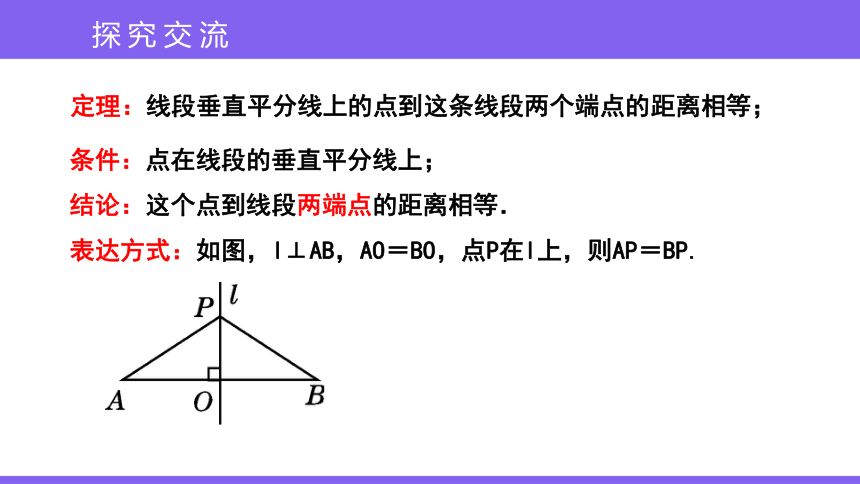
条件:点在线段的垂直平分线上;
结论:这个点到线段两端点的距离相等.
表达方式:如图,l⊥AB,AO=BO,点P在l上,则AP=BP.
定理:线段垂直平分线上的点到这条线段两个端点的距离相等;
探究交流
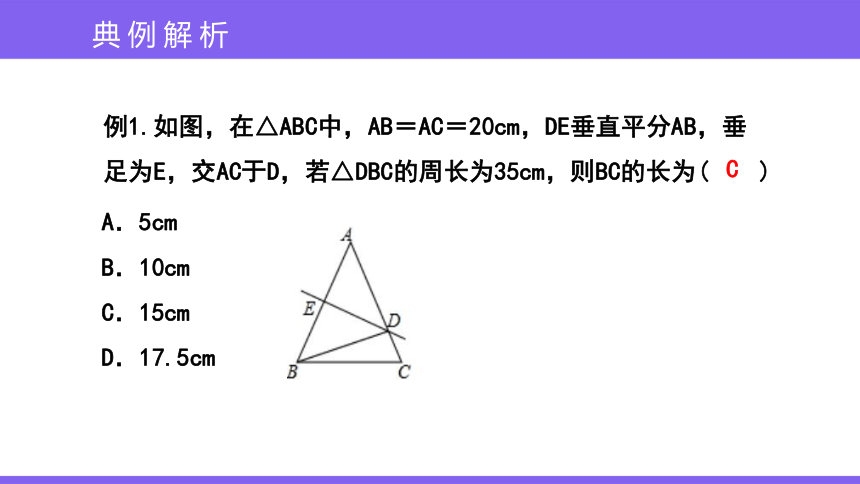
例1.如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,则BC的长为( )
A.5cm
B.10cm
C.15cm
D.17.5cm
C
典例解析
想一想
你能写出上面这个定理的逆命题吗?它是真命题吗?
定理:线段垂直平分线上的点到这条线段两个端点的距离相等.
逆
命
题
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
它是真命题吗?你能证明吗?
探究交流
如果有一个点到线段两个端点的距离相等,那么这个点在这条线段的垂直平分线上.
定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
探究交流
判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
条件:点到线段两端点距离相等;
结论:点在线段垂直平分线上.
表达方式:如图,∵PA=PB,∴点P在线段AB的垂直平分线上
探究交流
已知:线段 AB,点P是平面内一点且PA=PB.
求证:P点在AB的垂直平分线上.
A
B
C
P
证明一:过点P作已知线段 AB 的垂线 PC,PA=PB, PC=PC,
∴Rt△PAC≌Rt△PBC(HL).
∴AC=BC,
即P点在AB的垂直平分线上.
探究交流
证法二:取 AB 的中点 C,过 P,C 作直线.
∵AP = BP,PC = PC. AC = CB,
∴△APC ≌△BPC(SSS).
∴∠PCA =∠PCB(全等三角形的对应角相等).
又∵∠PCA +∠PCB = 180°,
∴∠PCA =∠PCB =∠90°,即 PC⊥AB.
∴ P 点在 AB 的垂直平分线上.
A
B
C
P
探究交流
例2.已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC.
求证:直线AO垂直平分线段BC.
A
B
C
O
典例解析
A
B
C
O
证明:∵ AB = AC.
∴ 点A在线段 BC 的垂直平分线上.(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
∴直线AO是线段BC的垂直平分线(两点确定一条直线).
同理,点 O 在线段 BC 的垂直平分线上.
典例解析
1.到三角形三个顶点的距离都相等的点是这个三角形的( )
A.三条高的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条边的垂直平分线的交点
巩固练习
2. 如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC与E,则△ADE的周长等于______.
A
B
C
D
E
巩固练习
3.如图①所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为( )
A.6 B.5 C.4 D.3
P
A
B
C
D
巩固练习
线段:在线段垂直平分线上的点到线段两个端点距离都相等.
判定:与线段两个端点距离相等的点都在线段的垂直平分线上.
线段垂直平分线的集合定义:
线段垂直平分线可以看作是与线段两个端点距离相等的所有点的集合.
课堂小结
第一章 三角形的证明
3.1 线段的垂直平分线
学习目标
1.理解线段垂直平分线的概念;
2.掌握线段垂直平分线的性质定理及逆定理;(重点)
3.能运用线段的垂直平分线的有关知识进行证明或计算.(难点)
情境导入
为了方便居民的生活,政府计划在三个住宅小区A、B、C之间新建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等?
A
B
C
探究交流
已知点A与点A′关于直线l对称,如果线段AA′沿直线l折叠,则点A与点A′重合,AD=A′D,∠1=∠2=90°,即直线l既平分线段AA′,又垂直线段AA′.
●
●
l
A
A′
D
2
1
(A)
我们把垂直且平分一条线段的直线叫作这条线段的垂直平分线.
由上可知:线段是轴对称图形,线段的垂直平分线是它的对称轴.
探究交流
作线段AB的中垂线MN,垂足为C;在MN上任取一点P,连结 PA、PB;
量一量 PA、PB 的长,你能发现什么?
A
B
M
N
C
P
定理 线段垂直平分线上的点到这条线段两个端点的距离相等.
探究交流
已知:如图,直线MN⊥AB,垂足是C,且AC=BC,P是MN上的任意一点。
求证:PA=PB。
证明:
∵MN⊥AB
∴∠PCA=∠PCB=90°
AC=BC
PC=PC
在 △PCA和△PBC中
∠PCA=∠PCB
∴ △PCA≌△PBC
∴PA=PB
N
M
B
A
P
C
探究交流
条件:点在线段的垂直平分线上;
结论:这个点到线段两端点的距离相等.
表达方式:如图,l⊥AB,AO=BO,点P在l上,则AP=BP.
定理:线段垂直平分线上的点到这条线段两个端点的距离相等;
探究交流
例1.如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,则BC的长为( )
A.5cm
B.10cm
C.15cm
D.17.5cm
C
典例解析
想一想
你能写出上面这个定理的逆命题吗?它是真命题吗?
定理:线段垂直平分线上的点到这条线段两个端点的距离相等.
逆
命
题
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
它是真命题吗?你能证明吗?
探究交流
如果有一个点到线段两个端点的距离相等,那么这个点在这条线段的垂直平分线上.
定理:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
探究交流
判定:到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
条件:点到线段两端点距离相等;
结论:点在线段垂直平分线上.
表达方式:如图,∵PA=PB,∴点P在线段AB的垂直平分线上
探究交流
已知:线段 AB,点P是平面内一点且PA=PB.
求证:P点在AB的垂直平分线上.
A
B
C
P
证明一:过点P作已知线段 AB 的垂线 PC,PA=PB, PC=PC,
∴Rt△PAC≌Rt△PBC(HL).
∴AC=BC,
即P点在AB的垂直平分线上.
探究交流
证法二:取 AB 的中点 C,过 P,C 作直线.
∵AP = BP,PC = PC. AC = CB,
∴△APC ≌△BPC(SSS).
∴∠PCA =∠PCB(全等三角形的对应角相等).
又∵∠PCA +∠PCB = 180°,
∴∠PCA =∠PCB =∠90°,即 PC⊥AB.
∴ P 点在 AB 的垂直平分线上.
A
B
C
P
探究交流
例2.已知:如图,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC.
求证:直线AO垂直平分线段BC.
A
B
C
O
典例解析
A
B
C
O
证明:∵ AB = AC.
∴ 点A在线段 BC 的垂直平分线上.(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
∴直线AO是线段BC的垂直平分线(两点确定一条直线).
同理,点 O 在线段 BC 的垂直平分线上.
典例解析
1.到三角形三个顶点的距离都相等的点是这个三角形的( )
A.三条高的交点
B.三条角平分线的交点
C.三条中线的交点
D.三条边的垂直平分线的交点
巩固练习
2. 如图,在△ABC中,BC=8,AB的中垂线交BC于D,AC的中垂线交BC与E,则△ADE的周长等于______.
A
B
C
D
E
巩固练习
3.如图①所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为( )
A.6 B.5 C.4 D.3
P
A
B
C
D
巩固练习
线段:在线段垂直平分线上的点到线段两个端点距离都相等.
判定:与线段两个端点距离相等的点都在线段的垂直平分线上.
线段垂直平分线的集合定义:
线段垂直平分线可以看作是与线段两个端点距离相等的所有点的集合.
课堂小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
