2.2 不等式的基本性质 课件(共17张PPT)
文档属性
| 名称 | 2.2 不等式的基本性质 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 18:29:56 | ||
图片预览






文档简介
(共15张PPT)
第二章 一元一次不等式与一元一次不等式组
2 不等式的基本性质
学习目标
1 理解并掌握不等式的基本性质.
2 能运用不等式的基本性质转化不等式为基本形式.
情境导入
等式的基本性质2:在等式两边都乘以或除以同一个数(除数不为0),结果仍相等.
等式的这些性质适用于不等式吗?不等式有哪些性质呢?
等式的基本性质1:在等式两边都加上(或减去)同一个数或整式,结果仍相等.
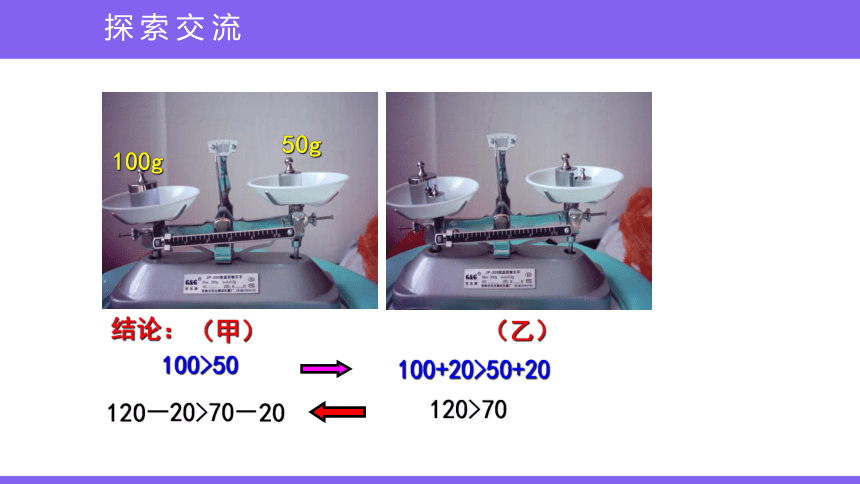
探索交流
(甲)
(乙)
100g
50g
结论:
100>50
100+20>50+20
120>70
120-20>70-20
(1)5>3, 5+2___3+2 , 5-2___3-2 ;
(2)-1<3, -1+2___3+2 , -1-3___3-3 ;
根据发现的规律填空:当不等式两边加或减同一个数(正数或负数)时,不等号的方向______.
不变
﹥
﹥
﹤
﹤
思考:用“﹥”或“﹤”填空,并总结其中的规律:
如果a>b,那么a+c>b+c,a-c>b-c.
不等式性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
探索交流
(3) 6>2, 6×5____2×5 , 6×(-5)____2×(-5) ;
(4)–2<3, (-2)×6___3×6 , (-2) ×(-6)___3×(-6 )
当不等式两边乘同一个正数时,不等号的方向_____;
而乘同一个负数时,不等号的方向_____;
改变
﹥
﹤
﹤
﹥
不变
如果a>b,c>0,那么ac____bc(或 )
不等式的性质2 不等式两边乘(或除以)同一个正数,不等号的方向不变.
>
探索交流
如果a>b,c<0,那么ac ___bc(或 )
﹤
不等式的性质3 不等式两边乘(或除以)同一个负数,不等号的方向改变.
探索交流
例1.将下列不等式化成“x > a”或“x < a”的形式:
(1)x - 5 > -1. (2)-2x > 3.
解:(1)根据不等式的基本性质1,在不等式两边都加5,得x - 5 + 5 > -1 + 5,即x > 4.
(2)根据不等式的基本性质3,在不等式两边都除以 -2,得x < .
典例解析
解:
(1)不等式的两边都加上5,由不等式基本性质1,得
x > -1 +5,
即 x > 4 .
例2.将下列不等式化成“x>a”“x<a”的形式.
(1)x-5>-1 ;
(2)-2x>3 ;
(2)不等式的两边都除以-2,由不等式基本性质3,得
典例解析
(3) x -7 < 8,
解:
不等式的两边都加上7,由不等式基本性质1,得
x -7+7 < 8+7,
即 x < 15 .
(3)x -7 < 8 ;
(4) 3x < 2x -3 .
(4) 3x < 2x -3,
不等式的两边都减去2x,由不等式基本性质1,得
3x -2x < 2x-3-2x,
即 x < -3.
典例解析
练习巩固
1.若x>y,则下列式子错误的是( ).
A. x-3 > y-3 B. -3x > -3y
C. x+3 > y+3 D.
2.有一道这样的题:“由★x>1得到x< ”,
则题中★表示的是( )
A.非正数 B.正数
C.非负数 D.负数
练习巩固
3. 下列说法不一定成立的是( ).
A. 若a > b,则a + c > b + c
B. 若a + c > b + c,则a > b
C.若a > b,则ac2 > bc2
D. 若ac2 > bc2,则a > b
练习巩固
不等式的基本性质1 不等式的两边都加(或减)同一个整式,不等号的方向不变.
不等式的基本性质2 不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
不等式的基本性质3 不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
课堂小结
第二章 一元一次不等式与一元一次不等式组
2 不等式的基本性质
学习目标
1 理解并掌握不等式的基本性质.
2 能运用不等式的基本性质转化不等式为基本形式.
情境导入
等式的基本性质2:在等式两边都乘以或除以同一个数(除数不为0),结果仍相等.
等式的这些性质适用于不等式吗?不等式有哪些性质呢?
等式的基本性质1:在等式两边都加上(或减去)同一个数或整式,结果仍相等.
探索交流
(甲)
(乙)
100g
50g
结论:
100>50
100+20>50+20
120>70
120-20>70-20
(1)5>3, 5+2___3+2 , 5-2___3-2 ;
(2)-1<3, -1+2___3+2 , -1-3___3-3 ;
根据发现的规律填空:当不等式两边加或减同一个数(正数或负数)时,不等号的方向______.
不变
﹥
﹥
﹤
﹤
思考:用“﹥”或“﹤”填空,并总结其中的规律:
如果a>b,那么a+c>b+c,a-c>b-c.
不等式性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.
探索交流
(3) 6>2, 6×5____2×5 , 6×(-5)____2×(-5) ;
(4)–2<3, (-2)×6___3×6 , (-2) ×(-6)___3×(-6 )
当不等式两边乘同一个正数时,不等号的方向_____;
而乘同一个负数时,不等号的方向_____;
改变
﹥
﹤
﹤
﹥
不变
如果a>b,c>0,那么ac____bc(或 )
不等式的性质2 不等式两边乘(或除以)同一个正数,不等号的方向不变.
>
探索交流
如果a>b,c<0,那么ac ___bc(或 )
﹤
不等式的性质3 不等式两边乘(或除以)同一个负数,不等号的方向改变.
探索交流
例1.将下列不等式化成“x > a”或“x < a”的形式:
(1)x - 5 > -1. (2)-2x > 3.
解:(1)根据不等式的基本性质1,在不等式两边都加5,得x - 5 + 5 > -1 + 5,即x > 4.
(2)根据不等式的基本性质3,在不等式两边都除以 -2,得x < .
典例解析
解:
(1)不等式的两边都加上5,由不等式基本性质1,得
x > -1 +5,
即 x > 4 .
例2.将下列不等式化成“x>a”“x<a”的形式.
(1)x-5>-1 ;
(2)-2x>3 ;
(2)不等式的两边都除以-2,由不等式基本性质3,得
典例解析
(3) x -7 < 8,
解:
不等式的两边都加上7,由不等式基本性质1,得
x -7+7 < 8+7,
即 x < 15 .
(3)x -7 < 8 ;
(4) 3x < 2x -3 .
(4) 3x < 2x -3,
不等式的两边都减去2x,由不等式基本性质1,得
3x -2x < 2x-3-2x,
即 x < -3.
典例解析
练习巩固
1.若x>y,则下列式子错误的是( ).
A. x-3 > y-3 B. -3x > -3y
C. x+3 > y+3 D.
2.有一道这样的题:“由★x>1得到x< ”,
则题中★表示的是( )
A.非正数 B.正数
C.非负数 D.负数
练习巩固
3. 下列说法不一定成立的是( ).
A. 若a > b,则a + c > b + c
B. 若a + c > b + c,则a > b
C.若a > b,则ac2 > bc2
D. 若ac2 > bc2,则a > b
练习巩固
不等式的基本性质1 不等式的两边都加(或减)同一个整式,不等号的方向不变.
不等式的基本性质2 不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
不等式的基本性质3 不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
课堂小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
