2.4.1 一元一次不等式 课件(共21张PPT)
文档属性
| 名称 | 2.4.1 一元一次不等式 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 18:28:06 | ||
图片预览





文档简介
(共17张PPT)
第二章 一元一次不等式与一元一次不等式组
4.1 一元一次不等式
学习目标
1.知道什么是一元一次不等式,会解简单的一元一次不等式并把解集表示在数轴上。(重点)
2.通过观察一元一次不等式的解法,对比解一元一次方程的步骤,归纳出解一元一次不等式的基本步骤。(难点)
情境导入
趣味阅读
有一次,鲁班的手不慎被一片小草叶子割破了,他发现小草叶子的边缘布满了密集的小齿,于是便产生联想,根据小草的结构发明了锯子.
鲁班在这里就运用了“类比”的思想方法,“类比”也是数学学习中常用的一种重要方法.
1.不等式的三条基本性质是什么
不等式的性质1 不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
不等式的性质3 不等式的两边乘(或除以)同一个负数,不等号的方向改变.
2.什么叫一元一次方程 解一元一次方程的步骤是什么
情境导入
只含有一个未知数、未知数的最高次数为1且两边都为整式的等式.
解一元一次方程的步骤:①去分母;②去括号;③移项;④合并同类项;⑤系数化为1.
情境导入
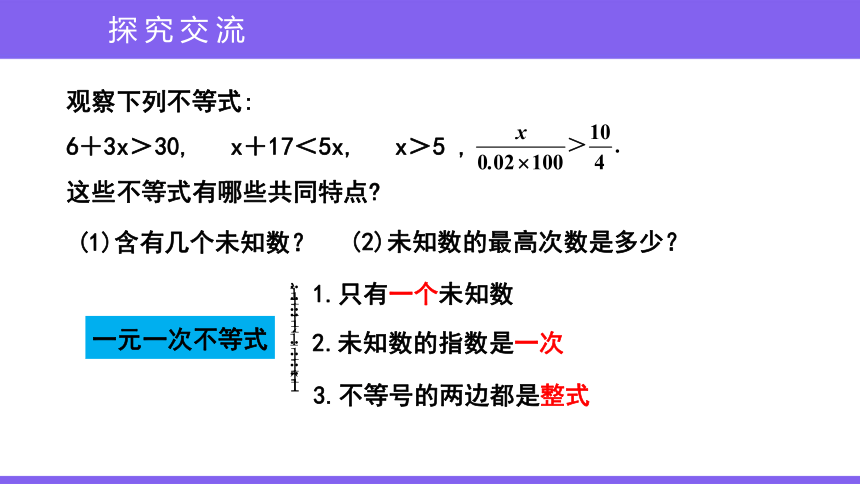
观察下列不等式:
6+3x>30, x+17<5x, x>5 ,
这些不等式有哪些共同特点
一元一次不等式
1.只有一个未知数
2.未知数的指数是一次
3.不等号的两边都是整式
(1)含有几个未知数?
(2)未知数的最高次数是多少?
探究交流
不等式的左右两边都是整式,只含有一个未知数,且未知数的最高次数是1,像这样的不等式称为一元一次不等式.
判别条件:
(1)都是整式;
(2)只含一个未知数;
(3)未知数的最高次数是1;
(4)未知是数的系数不为0.
探究交流
例1.解不等式3-x<2x+6,并把它的解集表示在数轴上.
解:两边都加 -2x,得
3 - x - 2x < 2x + 6 - 2x.
合并同类项,得 3 - 3x < 6.
两边都加-3,得 3- 3x - 3 < 6 - 3.
合并同类项,得 -3x < 3.
两边都除以-3,得 x > -1.
0
1
2
-1
-2
这个不等式的解集在数轴上的表示如图所示:
典例解析
例2.解不等式 ,并把它的解集表示在数轴上.
解:去分母,得3(x - 2) ≥ 2(7 - x).
去括号,得 3x - 6 ≥ 14 - 2x.
移项、合并同类项,得5x ≥ 20.
两边都除以5,得x ≥ 4.
这个不等式的解集在数轴上的表示如图所示:
5
6
7
4
3
2
1
0
典例解析
1.解一元一次不等式大致要分五个步骤进行:
(1)去分母;(2)去括号;(3)移项;
(4)合并同类项;(5)系数化1.?
2.在数轴上表示不等式的解集时,要注意不等号以及端点的情况.
归纳总结
解一元一次不等式与解一元一次方程的依据和步骤有什么异同点?
它们的依据不相同.解一元一次方程的依据是等式的性质,解一元一次不等式的依据是不等式的性质.
它们的步骤基本相同,都是去分母、去括号、移项、合并同类项、未知数的系数化为1.
这些步骤中,要特别注意的是:不等式两边都乘(或除以)同一个负数,必须改变不等号的方向.这是与解一元一次方程不同的地方.
归纳总结
1.解不等式 ≥x-1,下列去分母正确的是( )
A.2x+1-3x-1≥x-1
B.2(x+1)-3(x-1)≥x-1
C.2x+1-3x-1≥6x-1
D.2(x+1)-3(x-1)≥6(x-1)
练习巩固
2.解不等式 的过程中,开始出现错误的一步是( )
①去分母,得5(x+2)>3(2x-1);
②去括号,得5x+10>6x-3;
③移项、合并同类项,得-x>-13;
④系数化为1,得x>13.
A.① B.② C.③ D.④
练习巩固
3.求不等式4(x + 1)≤ 24的正整数解.
练习巩固
解一元一次不等式的一般步骤
(1)去分母———不等式性质2或3
注意:①勿漏乘不含分母的项;②分子是两项或两项以上的代数式时要加括号;③若两边同时乘一个负数,须注意不等号的方向要改变.
(2)去括号——去括号法则和分配律
注意:①勿漏乘括号内每一项;②括号前面是“-”号,括号内各项要变号.
课堂小结
(3)移项——移项法则(不等式性质1)
注意:移项要变号.
(4)合并同类项——合并同类项法则.
(5)把系数化成1——不等式基本性质2或性质3.
注意:两边同时除以未知数的系数时,要分清不等号的方向是否改变.
课堂小结
第二章 一元一次不等式与一元一次不等式组
4.1 一元一次不等式
学习目标
1.知道什么是一元一次不等式,会解简单的一元一次不等式并把解集表示在数轴上。(重点)
2.通过观察一元一次不等式的解法,对比解一元一次方程的步骤,归纳出解一元一次不等式的基本步骤。(难点)
情境导入
趣味阅读
有一次,鲁班的手不慎被一片小草叶子割破了,他发现小草叶子的边缘布满了密集的小齿,于是便产生联想,根据小草的结构发明了锯子.
鲁班在这里就运用了“类比”的思想方法,“类比”也是数学学习中常用的一种重要方法.
1.不等式的三条基本性质是什么
不等式的性质1 不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
不等式的性质3 不等式的两边乘(或除以)同一个负数,不等号的方向改变.
2.什么叫一元一次方程 解一元一次方程的步骤是什么
情境导入
只含有一个未知数、未知数的最高次数为1且两边都为整式的等式.
解一元一次方程的步骤:①去分母;②去括号;③移项;④合并同类项;⑤系数化为1.
情境导入
观察下列不等式:
6+3x>30, x+17<5x, x>5 ,
这些不等式有哪些共同特点
一元一次不等式
1.只有一个未知数
2.未知数的指数是一次
3.不等号的两边都是整式
(1)含有几个未知数?
(2)未知数的最高次数是多少?
探究交流
不等式的左右两边都是整式,只含有一个未知数,且未知数的最高次数是1,像这样的不等式称为一元一次不等式.
判别条件:
(1)都是整式;
(2)只含一个未知数;
(3)未知数的最高次数是1;
(4)未知是数的系数不为0.
探究交流
例1.解不等式3-x<2x+6,并把它的解集表示在数轴上.
解:两边都加 -2x,得
3 - x - 2x < 2x + 6 - 2x.
合并同类项,得 3 - 3x < 6.
两边都加-3,得 3- 3x - 3 < 6 - 3.
合并同类项,得 -3x < 3.
两边都除以-3,得 x > -1.
0
1
2
-1
-2
这个不等式的解集在数轴上的表示如图所示:
典例解析
例2.解不等式 ,并把它的解集表示在数轴上.
解:去分母,得3(x - 2) ≥ 2(7 - x).
去括号,得 3x - 6 ≥ 14 - 2x.
移项、合并同类项,得5x ≥ 20.
两边都除以5,得x ≥ 4.
这个不等式的解集在数轴上的表示如图所示:
5
6
7
4
3
2
1
0
典例解析
1.解一元一次不等式大致要分五个步骤进行:
(1)去分母;(2)去括号;(3)移项;
(4)合并同类项;(5)系数化1.?
2.在数轴上表示不等式的解集时,要注意不等号以及端点的情况.
归纳总结
解一元一次不等式与解一元一次方程的依据和步骤有什么异同点?
它们的依据不相同.解一元一次方程的依据是等式的性质,解一元一次不等式的依据是不等式的性质.
它们的步骤基本相同,都是去分母、去括号、移项、合并同类项、未知数的系数化为1.
这些步骤中,要特别注意的是:不等式两边都乘(或除以)同一个负数,必须改变不等号的方向.这是与解一元一次方程不同的地方.
归纳总结
1.解不等式 ≥x-1,下列去分母正确的是( )
A.2x+1-3x-1≥x-1
B.2(x+1)-3(x-1)≥x-1
C.2x+1-3x-1≥6x-1
D.2(x+1)-3(x-1)≥6(x-1)
练习巩固
2.解不等式 的过程中,开始出现错误的一步是( )
①去分母,得5(x+2)>3(2x-1);
②去括号,得5x+10>6x-3;
③移项、合并同类项,得-x>-13;
④系数化为1,得x>13.
A.① B.② C.③ D.④
练习巩固
3.求不等式4(x + 1)≤ 24的正整数解.
练习巩固
解一元一次不等式的一般步骤
(1)去分母———不等式性质2或3
注意:①勿漏乘不含分母的项;②分子是两项或两项以上的代数式时要加括号;③若两边同时乘一个负数,须注意不等号的方向要改变.
(2)去括号——去括号法则和分配律
注意:①勿漏乘括号内每一项;②括号前面是“-”号,括号内各项要变号.
课堂小结
(3)移项——移项法则(不等式性质1)
注意:移项要变号.
(4)合并同类项——合并同类项法则.
(5)把系数化成1——不等式基本性质2或性质3.
注意:两边同时除以未知数的系数时,要分清不等号的方向是否改变.
课堂小结
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
