北师大版八年级数学下册3.3中心对称课件(共21张PPT)
文档属性
| 名称 | 北师大版八年级数学下册3.3中心对称课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-13 13:31:12 | ||
图片预览





文档简介
(共21张PPT)
3.3 中心对称
课程讲授
新知导入
随堂练习
课堂小结
第三章 图形的平移与旋转
知识要点
1.中心对称的概念和性质
2.中心对称图形
新知导入
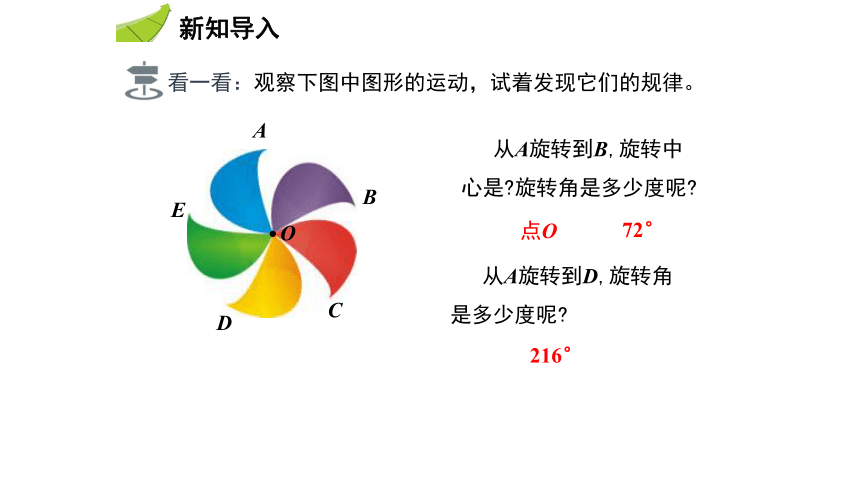
看一看:观察下图中图形的运动,试着发现它们的规律。
E
A
B
C
D
从A旋转到B,旋转中心是 旋转角是多少度呢
从A旋转到D,旋转角是多少度呢
O
点O
72°
216°
课程讲授
1
中心对称的概念和性质
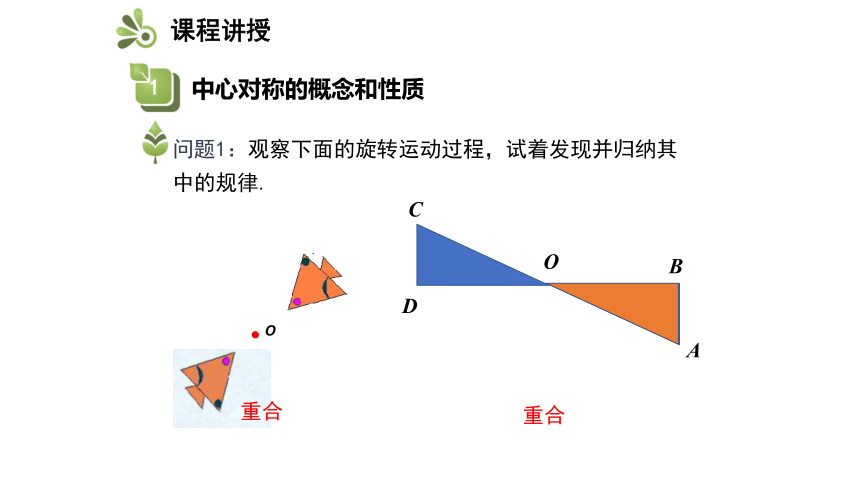
问题1:观察下面的旋转运动过程,试着发现并归纳其中的规律.
O
重合
B
A
D
O
C
重合
课程讲授
1
中心对称的概念和性质
B
A
D
O
C
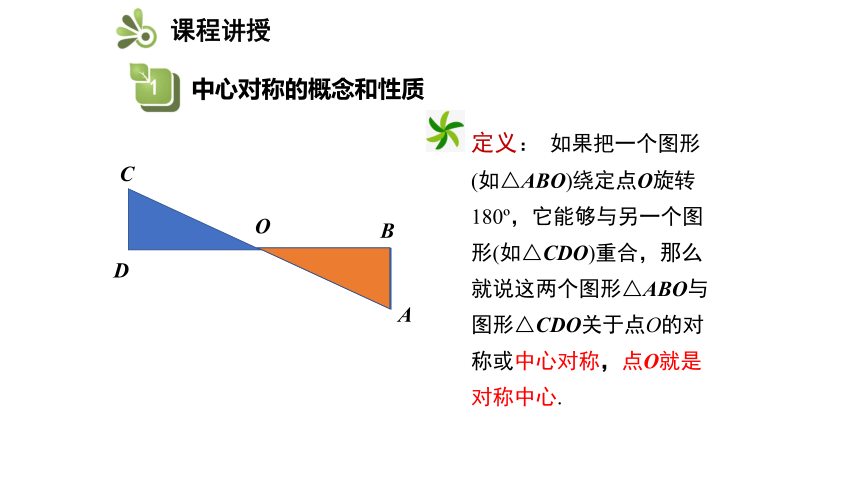
定义: 如果把一个图形
(如△ABO)绕定点O旋转
180 ,它能够与另一个图
形(如△CDO)重合,那么
就说这两个图形△ABO与
图形△CDO关于点O的对
称或中心对称,点O就是
对称中心.
课程讲授
1
中心对称的概念和性质
归纳:中心对称是一种特殊的旋转.其旋转角是180 °.中心对称是两个图形之间一种特殊的位置关系.
课程讲授
1
中心对称的概念和性质
练一练:下列两个电子数字成中心对称的是( )
A
课程讲授
1
中心对称的概念和性质
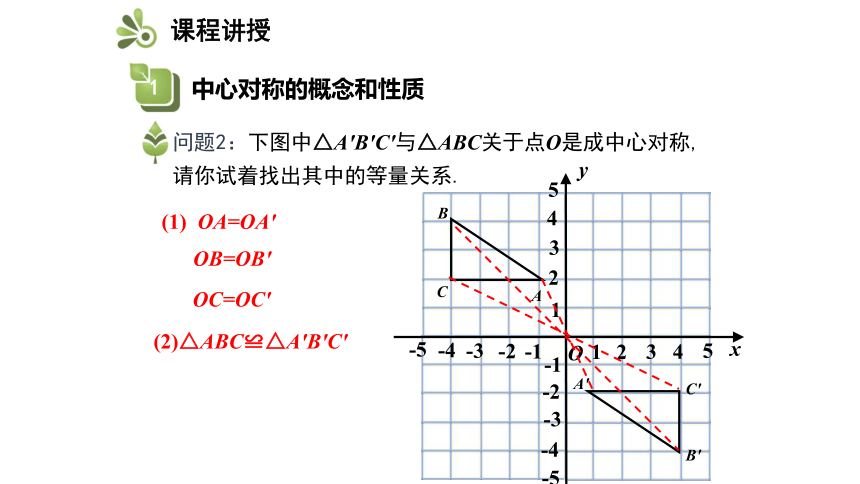
问题2:下图中△A′B′C′与△ABC关于点O是成中心对称,请你试着找出其中的等量关系.
-1
-2
-3
-4
5
1
-2
3
-4
-5
-1
2
-3
4
-5
1
2
3
4
5
y
O
x
C′
A′
B′
C
A
B
OC=OC′
(2)△ABC≌△A′B′C′
(1) OA=OA′
OB=OB′
课程讲授
1
中心对称的概念和性质
中心对称的性质:
(1)成中心对称的两个图形中,对应点所连线段经过_______,且被_________平分.(即______与________三点共线);
(2)中心对称的两个图形是______.
对称中心
对称中心
对称点
对称中心
全等形
课程讲授
1
中心对称的概念和性质
练一练:如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A′是对称点
B.BO=B′O
C.AB∥A′B′
D.∠ACB=∠C′A′B′
D
课程讲授
2
中心对称图形
问题1.1:如图,将线段AB绕它的中点旋转180°,你有什么发现?
B
A
O
绕O点旋转了180度后与原线段重合
课程讲授
2
中心对称图形
问题1.2:如图,将平行四边形ABCD绕它的两条对角线的交点O旋转180°,你有什么发现?
A
B
C
D
O
绕O点旋转了180度后与原平行四边形重合
课程讲授
2
中心对称图形
A
B
C
D
O
定义:把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
课程讲授
2
中心对称图形
练一练:下列美丽的壮锦图案是中心对称图形的是( )
A
随堂练习
O1
1.如图,四边形ABCD与四边形FGHE关于一个点成中心对称,则这个点是________.
随堂练习
2.如图,△ABC和△AB′C′成中心对称,点A为对称中心.若∠C=90°,∠B=30°,AC=1,则BB′的长为( )
A.4
B.
C.
D.
A
随堂练习
3.在学习《图形变化的简单应用》这一节时,老师要求同学们利用图形变化设计图案.下列设计的图案中,是中心对称图形但不是轴对称图形的是( )
C
4.张扑克牌按如图1所示的方式放在桌子上,小敏把其中两张旋转180°后如图2所示,那么她所旋转的牌从左起是( )
A.第一张、第二张
B.第二张、第三张
C.第三张、第四张
D.第四张、第一张
随堂练习
A
随堂练习
5.如图,在平面直角坐标系中,若△ABC与△A1B1C1
关于点E成中心对称,则对称中心点E的坐标是( )
A.(0,0)
B.(2,0)
C.(3,0)
D.(3,-1)
D
随堂练习
6.如图,△ABC和△DEF是成中心对称的两个三角形,请找出它们的对称中心.
O
课堂小结
中心对称
定义
中心对称的性质
如果把一个图形绕定点O旋转180 ,它能够与另一个图形重合,那么就说这两个图形关于点O的对称或中心对称,点O就是对称中心.
(1)成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.(即对称点与对称中心三点共线);
(2)中心对称的两个图形是全等形.
中心对称图形
判断依据:绕着内部一点旋转180度能与本身重合的图形
3.3 中心对称
课程讲授
新知导入
随堂练习
课堂小结
第三章 图形的平移与旋转
知识要点
1.中心对称的概念和性质
2.中心对称图形
新知导入
看一看:观察下图中图形的运动,试着发现它们的规律。
E
A
B
C
D
从A旋转到B,旋转中心是 旋转角是多少度呢
从A旋转到D,旋转角是多少度呢
O
点O
72°
216°
课程讲授
1
中心对称的概念和性质
问题1:观察下面的旋转运动过程,试着发现并归纳其中的规律.
O
重合
B
A
D
O
C
重合
课程讲授
1
中心对称的概念和性质
B
A
D
O
C
定义: 如果把一个图形
(如△ABO)绕定点O旋转
180 ,它能够与另一个图
形(如△CDO)重合,那么
就说这两个图形△ABO与
图形△CDO关于点O的对
称或中心对称,点O就是
对称中心.
课程讲授
1
中心对称的概念和性质
归纳:中心对称是一种特殊的旋转.其旋转角是180 °.中心对称是两个图形之间一种特殊的位置关系.
课程讲授
1
中心对称的概念和性质
练一练:下列两个电子数字成中心对称的是( )
A
课程讲授
1
中心对称的概念和性质
问题2:下图中△A′B′C′与△ABC关于点O是成中心对称,请你试着找出其中的等量关系.
-1
-2
-3
-4
5
1
-2
3
-4
-5
-1
2
-3
4
-5
1
2
3
4
5
y
O
x
C′
A′
B′
C
A
B
OC=OC′
(2)△ABC≌△A′B′C′
(1) OA=OA′
OB=OB′
课程讲授
1
中心对称的概念和性质
中心对称的性质:
(1)成中心对称的两个图形中,对应点所连线段经过_______,且被_________平分.(即______与________三点共线);
(2)中心对称的两个图形是______.
对称中心
对称中心
对称点
对称中心
全等形
课程讲授
1
中心对称的概念和性质
练一练:如图,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( )
A.点A与点A′是对称点
B.BO=B′O
C.AB∥A′B′
D.∠ACB=∠C′A′B′
D
课程讲授
2
中心对称图形
问题1.1:如图,将线段AB绕它的中点旋转180°,你有什么发现?
B
A
O
绕O点旋转了180度后与原线段重合
课程讲授
2
中心对称图形
问题1.2:如图,将平行四边形ABCD绕它的两条对角线的交点O旋转180°,你有什么发现?
A
B
C
D
O
绕O点旋转了180度后与原平行四边形重合
课程讲授
2
中心对称图形
A
B
C
D
O
定义:把一个图形绕某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
课程讲授
2
中心对称图形
练一练:下列美丽的壮锦图案是中心对称图形的是( )
A
随堂练习
O1
1.如图,四边形ABCD与四边形FGHE关于一个点成中心对称,则这个点是________.
随堂练习
2.如图,△ABC和△AB′C′成中心对称,点A为对称中心.若∠C=90°,∠B=30°,AC=1,则BB′的长为( )
A.4
B.
C.
D.
A
随堂练习
3.在学习《图形变化的简单应用》这一节时,老师要求同学们利用图形变化设计图案.下列设计的图案中,是中心对称图形但不是轴对称图形的是( )
C
4.张扑克牌按如图1所示的方式放在桌子上,小敏把其中两张旋转180°后如图2所示,那么她所旋转的牌从左起是( )
A.第一张、第二张
B.第二张、第三张
C.第三张、第四张
D.第四张、第一张
随堂练习
A
随堂练习
5.如图,在平面直角坐标系中,若△ABC与△A1B1C1
关于点E成中心对称,则对称中心点E的坐标是( )
A.(0,0)
B.(2,0)
C.(3,0)
D.(3,-1)
D
随堂练习
6.如图,△ABC和△DEF是成中心对称的两个三角形,请找出它们的对称中心.
O
课堂小结
中心对称
定义
中心对称的性质
如果把一个图形绕定点O旋转180 ,它能够与另一个图形重合,那么就说这两个图形关于点O的对称或中心对称,点O就是对称中心.
(1)成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.(即对称点与对称中心三点共线);
(2)中心对称的两个图形是全等形.
中心对称图形
判断依据:绕着内部一点旋转180度能与本身重合的图形
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
