安徽省马鞍山市12—13学年度高二上学期期末素质测试数学理
文档属性
| 名称 | 安徽省马鞍山市12—13学年度高二上学期期末素质测试数学理 |  | |
| 格式 | zip | ||
| 文件大小 | 174.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-18 23:22:24 | ||
图片预览



文档简介
马鞍山市第二中学2012—2013学年度
第一学期期终素质测试
高二数学试题(理科)
命题人 聂晓峰 审题人 张以虎
一、选择题(本大题共10小题,每小题5分,计50分)
1.命题“若a、b都是偶数,则a+b是偶数”的逆否命题是(▲▲)
A、若a+b不是偶数,则a、b都不是偶数 B、若a+b不是偶数,则a、b不都是偶数
C、若a、b都不是偶数,则a+b不是偶数 D、若a、b不都是偶数,则a+b不是偶数
2.“直线y=kx+1的倾斜角为钝角”的一个必要不充分条件是(▲▲)
A、k<0 B、k<-1 C、k<1 D、k>-2
3.下列语句为特称命题且为假命题的是(▲▲)
A、指数函数都是增函数 B、有一个事件的概率大于1吗?
C、有些三角形没有外接圆 D、存在一个实数x,使x2≤0
4.椭圆的焦点坐标为(▲▲)
A、(3, 0),(-3, 0) B、(0, 3),(0, -3) C、(2, 0),(-2, 0) D、(0, 2),(0, -2)
5.双曲线的渐近线方程为(▲▲)
A、y=±3x B、y=±x C、y=±x D、y=±x
6.过点(1, 1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有(▲▲)
A、1条 B、2条 C、3条 D、0条
7.已知S是⊿ABC所在平面外一点,D是SC的中点,若=x+y+z,则x+y+z的值为(▲▲)
A、0 B、1 C、2 D、3
8.若a、b、c为任意向量,λ∈R,下列等式不一定成立的是(▲▲)
A、(a+b)+c= a+(b+c) B、(a+b)·c= a·b+ a·c C、λ(a+b)=λa+λb D、(a·b)c= a(b·c)
9.已知A(x, 5-x, 2x-1),B(1, x+2, 2-x),当||取最小值时,x的值等于(▲▲)
A、 B、- C、19 D、
10.将正方形ABCD沿对角线AC折成直二面角,则异面直线AB与CD的夹角的余弦值是(▲▲)
A、- B、 C、 D、
二、填空题(本大题5小题,每小题5分,计25分)
11.在⊿ABC中,“A12.双曲线上一点P到右焦点的距离是实轴两端点到右焦点距离的等差中项,则点P到左焦点的距离为 ▲▲▲▲ ;
13.抛物线y=x2的焦点坐标是 ▲▲▲▲ ;
14.已知a=(1, 1, 0),b=(1, 1 ,1 ),若b=b1+b2,且b1∥a,b2⊥a,则b1=▲▲▲▲、b2=▲▲▲▲;
15.已知空间四边形ABCD的四条边和对角线长都为a,点E、F、G分别是AB,AD,DC的中点,则四个数量积①·;②·;③·;④·中,其中运算结果为的式子的序号为 ▲▲▲▲ ;
三、解答题(本大题共6小题,计75分)
16.(12分)给定两个命题:命题甲:关于x的不等式x 2 + (a-1)x +a2 ≤0的解集为Ф;命题乙:函数f (x)=(2a2-a) x在R上是增函数。分别求出符合下列条件的实数a的取值范围。
(1) 甲、乙中至少有一个是真命题;(2)甲、乙中有且仅有一个是真命题。
17.(12分)已知抛物线C:x2=2py(p>0)上一点A(m, 4)到其焦点F的距离为。
(1)求p与m的值;
(2)若直线l过焦点F交抛物线于P,Q两点,且|PQ|=5,求直线l的方程。
18.(12分)若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+。求证:a,b,c中至少有一个大于0。
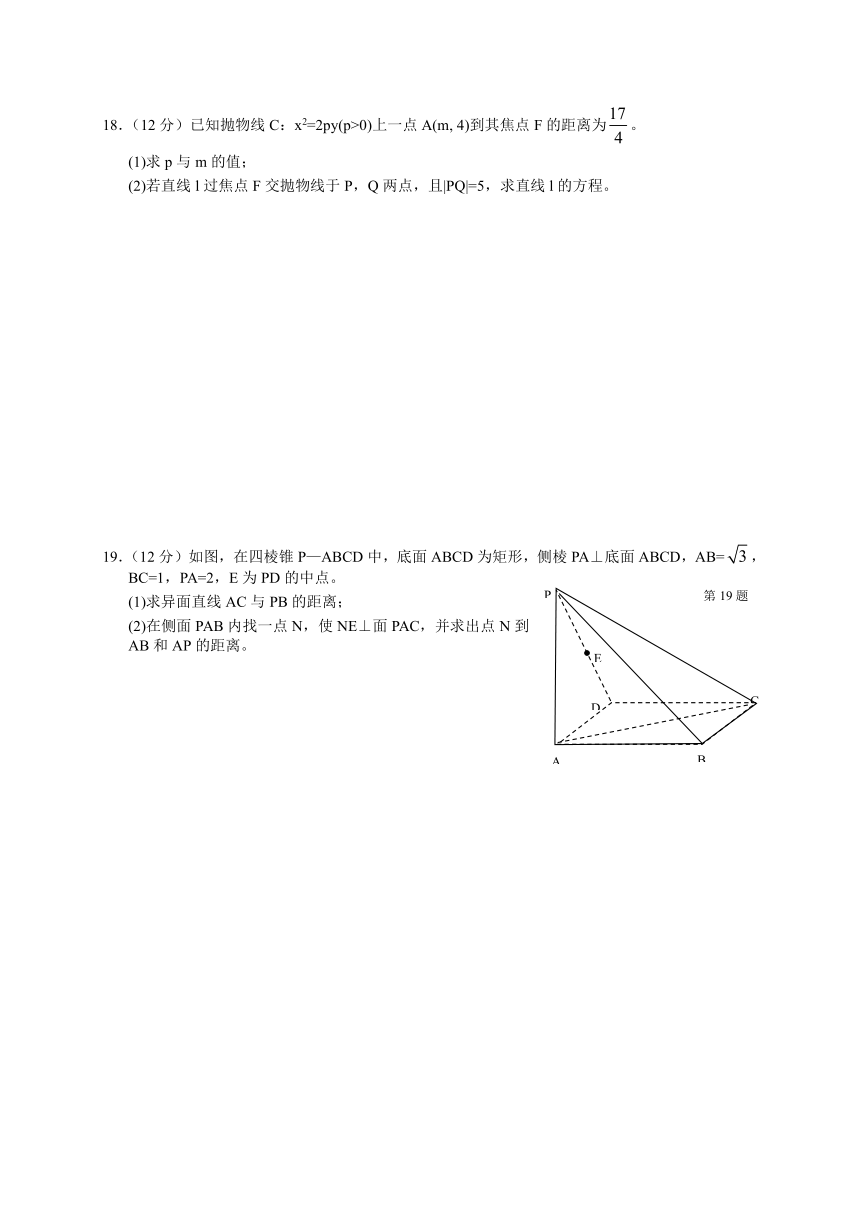
19.(12分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点。
(1)求异面直线AC与PB的距离;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离。
20.(13分)如图,⊿BCD与⊿MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2。
(1)求直线AM与平面BCD所成角的大小;
(2)求平面ACM与平面BCD所成二面角的正弦值。
21、(14分)设椭圆C:的右焦点为F,过点F的直线l与椭圆C相交于A、B两点,直线l的倾斜角为60 ,且。
(1)求椭圆C的离心率;(2)如果|AB|=,求椭圆C的方程。
*******此页自行保存,只要上交答题卷,请将有关答案填入相应答题栏*******
2012-2013学年度第一学期期末考试高二数学理科***答题卷***
一、选择题(5×10=50)
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题(5×5=25)
11)、 ; 12)、 ; 13)、 ;
14)、 ; 15)、 。
三、解答题(本大题共6小题,计75分)
16.(12分)给定两个命题:命题甲:关于x的不等式x 2 + (a-1)x +a2 ≤0的解集为Ф;命题乙:函数f (x)=(2a2-a) x在R上是增函数。分别求出符合下列条件的实数a的取值范围。
(1) 甲、乙中至少有一个是真命题;(2)甲、乙中有且仅有一个是真命题。
17.(12分)若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+。求证:a,b,c中至少有一个大于0。
18.(12分)已知抛物线C:x2=2py(p>0)上一点A(m, 4)到其焦点F的距离为。
(1)求p与m的值;
(2)若直线l过焦点F交抛物线于P,Q两点,且|PQ|=5,求直线l的方程。
19.(12分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点。
(1)求异面直线AC与PB的距离;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离。
20.(13分)如图,⊿BCD与⊿MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2。
(1)求直线AM与平面BCD所成角的大小;
21、(14分)设椭圆C:的右焦点为F,过点F的直线l与椭圆C相交于A、B两点,直线l的倾斜角为60 ,。
(1)求椭圆C的离心率;
(2)如果|AB|=,求椭圆C的方程。
参考答案
一、选择题(3×12=36)
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C D B A A D A B
二、填空题(4×5=20)
11)、 充要条件 ; 12)、 13 ; 13)、 (0, 1) ;
14)、 (1, 1, 0) ; (0, 0, 1) ; 15)、 ②③ 。
三、解答题(本大题共6小题,计75分)
16.(12分)给定两个命题:命题甲:关于x的不等式x2 + (a-1)x +a2 ≤0的解集为Ф;命题乙:函数f (x)=(2a2-a) x在R上是增函数。分别求出符合下列条件的实数a的取值范围。
(1) 甲、乙中至少有一个是真命题;(2)甲、乙中有且仅有一个是真命题。
解:由甲命题为真,得(a-1)2-4a2<0, (3a-1)(a+1)>0,∴a< -1或a>,
由乙命题为真,得2a2-a>1, (2a+1)(a-1)>0,∴a< -或a>1。 ………4分
(1)若甲、乙全假,可得a∈[-,],故所求范围是(-∞, -)∪(, +∞) ………8分
(2)若甲、乙全真,可得a∈(-∞, -1)∪(1, +∞),故所求范围是[-1, -)∪(,1] ………12分
17.(12分)若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+。求证:a,b,c中至少有一个大于0。
解:假设a、b、c均不大于零,则a+b+c≤0 (*) ………2分
而由已知得,a+b+c=x2-2x+y2-2y+z2-2z+++=(x-1)2+(y-1)2+(z-1)2+π-3 ………8分
由于π-3<0,所以a+b+c>0,与(*)式矛盾,故假设错误,
所以,原命题成立。 ………12分
18.(12分)已知抛物线C:x2=2py(p>0)上一点A(m, 4)到其焦点F的距离为。
(1)求p与m的值;
(2)若直线l过焦点F交抛物线于P,Q两点,且|PQ|=5,求直线l的方程。
解:(1)依题=4+,∴p=,x2=y,∴m2=4,m=±2 ………5分
(2)依题可设PQ的方程为l:y=kx+,与x2=y联立,消去x,得y2-(+k2)y+=0,
∴y1+y2=+k2,而|PQ|= y1+y2+p=1+k2,k2=5-1=4,k=±2 ………10分
∴直线l的方程为y=2x+或y= -2x+, ………12分
19.(12分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点。
(1)求异面直线AC与PB的距离;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离。
答案:(1)、;(2)1;。
解析:以A为原点,以向量的方向为坐标轴方向建立空间直角坐标系,利用向量条件下的距离公式求解,以下省略。
20.(13分)如图,⊿BCD与⊿MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2。
(1)求直线AM与平面BCD所成角的大小;
(2)求平面ACM与平面BCD所成二面角的正弦值。
解:(1)取CD中点O,则MO⊥CD,
∵面MCD⊥面BCD交于CD,∴MO⊥面BCD,
又AB⊥面BCD,∴AB∥MO。
取AB中点F,连OF,由题设可知MO=,AF=,
∴OF∥AM,故OF与平面BCD所成的角等于所求的角。
而在Rt⊿BEF中,BO=,BF=,∠BOF=45 ,即所求的角为45 。 ………6分
(2)延长BO、AM相交于点G,∵MO∥AB且MO=AB,
∴OG=BO=,又CO=1,∴CG=2,作EH⊥CG于H,
由于ME⊥平面BCD,则MH⊥CG,∴∠MHO即为所求二面角的平面角。
在Rt⊿OCG中,由OH·CG=OC·OG,得OH=,
从而MH=,∴sin∠MHO=。 ………13分
另解:依题易知OB、OC、OM两两垂直,故可以如图建立空间直角坐标系,利用空间向量进行求解,过程略。
21、(14分)设椭圆C:的右焦点为F,过F的直线l与椭圆C相交于A、B两点,直线l的倾斜角为60 ,。
(1)求椭圆C的离心率;(2)如果|AB|=,求椭圆C的方程。
解:(1)设F(c, 0),则c2=a2-b2,且直线l的方程为y=(x-c),设A(x1, y1)、B(x2, y2),
由,得,∴y1+y2= -y2,y1y2=-2y22,
联立直线l与椭圆C的方程,并消元、整理,得,
于是 4a2=9c2,∴e=; ………7分
(2)∵|AB|=,∴ ①; 由e=,得5a2=9b2 ②,
联立①②解得a=3,b2=5,∴椭圆C的方程为 ………14分
马鞍山市第二中学2012—2013学年度
第一学期期终素质测试
高二数学试题(理科)
命题人 聂晓峰 审题人 张以虎
一、选择题(本大题共10小题,每小题5分,计50分)
1.命题“若a、b都是偶数,则a+b是偶数”的逆否命题是(▲▲)
A、若a+b不是偶数,则a、b都不是偶数 B、若a+b不是偶数,则a、b不都是偶数
C、若a、b都不是偶数,则a+b不是偶数 D、若a、b不都是偶数,则a+b不是偶数
2.“直线y=kx+1的倾斜角为钝角”的一个必要不充分条件是(▲▲)
A、k<0 B、k<-1 C、k<1 D、k>-2
3.下列语句为特称命题且为假命题的是(▲▲)
A、指数函数都是增函数 B、有一个事件的概率大于1吗?
C、有些三角形没有外接圆 D、存在一个实数x,使x2≤0
4.椭圆的焦点坐标为(▲▲)
A、(3, 0),(-3, 0) B、(0, 3),(0, -3) C、(2, 0),(-2, 0) D、(0, 2),(0, -2)
5.双曲线的渐近线方程为(▲▲)
A、y=±3x B、y=±x C、y=±x D、y=±x
6.过点(1, 1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有(▲▲)
A、1条 B、2条 C、3条 D、0条
7.已知S是⊿ABC所在平面外一点,D是SC的中点,若=x+y+z,则x+y+z的值为(▲▲)
A、0 B、1 C、2 D、3
8.若a、b、c为任意向量,λ∈R,下列等式不一定成立的是(▲▲)
A、(a+b)+c= a+(b+c) B、(a+b)·c= a·b+ a·c C、λ(a+b)=λa+λb D、(a·b)c= a(b·c)
9.已知A(x, 5-x, 2x-1),B(1, x+2, 2-x),当||取最小值时,x的值等于(▲▲)
A、 B、- C、19 D、
10.将正方形ABCD沿对角线AC折成直二面角,则异面直线AB与CD的夹角的余弦值是(▲▲)
A、- B、 C、 D、
二、填空题(本大题5小题,每小题5分,计25分)
11.在⊿ABC中,“A12.双曲线上一点P到右焦点的距离是实轴两端点到右焦点距离的等差中项,则点P到左焦点的距离为 ▲▲▲▲ ;
13.抛物线y=x2的焦点坐标是 ▲▲▲▲ ;
14.已知a=(1, 1, 0),b=(1, 1 ,1 ),若b=b1+b2,且b1∥a,b2⊥a,则b1=▲▲▲▲、b2=▲▲▲▲;
15.已知空间四边形ABCD的四条边和对角线长都为a,点E、F、G分别是AB,AD,DC的中点,则四个数量积①·;②·;③·;④·中,其中运算结果为的式子的序号为 ▲▲▲▲ ;
三、解答题(本大题共6小题,计75分)
16.(12分)给定两个命题:命题甲:关于x的不等式x 2 + (a-1)x +a2 ≤0的解集为Ф;命题乙:函数f (x)=(2a2-a) x在R上是增函数。分别求出符合下列条件的实数a的取值范围。
(1) 甲、乙中至少有一个是真命题;(2)甲、乙中有且仅有一个是真命题。
17.(12分)已知抛物线C:x2=2py(p>0)上一点A(m, 4)到其焦点F的距离为。
(1)求p与m的值;
(2)若直线l过焦点F交抛物线于P,Q两点,且|PQ|=5,求直线l的方程。
18.(12分)若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+。求证:a,b,c中至少有一个大于0。
19.(12分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点。
(1)求异面直线AC与PB的距离;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离。
20.(13分)如图,⊿BCD与⊿MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2。
(1)求直线AM与平面BCD所成角的大小;
(2)求平面ACM与平面BCD所成二面角的正弦值。
21、(14分)设椭圆C:的右焦点为F,过点F的直线l与椭圆C相交于A、B两点,直线l的倾斜角为60 ,且。
(1)求椭圆C的离心率;(2)如果|AB|=,求椭圆C的方程。
*******此页自行保存,只要上交答题卷,请将有关答案填入相应答题栏*******
2012-2013学年度第一学期期末考试高二数学理科***答题卷***
一、选择题(5×10=50)
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题(5×5=25)
11)、 ; 12)、 ; 13)、 ;
14)、 ; 15)、 。
三、解答题(本大题共6小题,计75分)
16.(12分)给定两个命题:命题甲:关于x的不等式x 2 + (a-1)x +a2 ≤0的解集为Ф;命题乙:函数f (x)=(2a2-a) x在R上是增函数。分别求出符合下列条件的实数a的取值范围。
(1) 甲、乙中至少有一个是真命题;(2)甲、乙中有且仅有一个是真命题。
17.(12分)若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+。求证:a,b,c中至少有一个大于0。
18.(12分)已知抛物线C:x2=2py(p>0)上一点A(m, 4)到其焦点F的距离为。
(1)求p与m的值;
(2)若直线l过焦点F交抛物线于P,Q两点,且|PQ|=5,求直线l的方程。
19.(12分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点。
(1)求异面直线AC与PB的距离;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离。
20.(13分)如图,⊿BCD与⊿MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2。
(1)求直线AM与平面BCD所成角的大小;
21、(14分)设椭圆C:的右焦点为F,过点F的直线l与椭圆C相交于A、B两点,直线l的倾斜角为60 ,。
(1)求椭圆C的离心率;
(2)如果|AB|=,求椭圆C的方程。
参考答案
一、选择题(3×12=36)
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C D B A A D A B
二、填空题(4×5=20)
11)、 充要条件 ; 12)、 13 ; 13)、 (0, 1) ;
14)、 (1, 1, 0) ; (0, 0, 1) ; 15)、 ②③ 。
三、解答题(本大题共6小题,计75分)
16.(12分)给定两个命题:命题甲:关于x的不等式x2 + (a-1)x +a2 ≤0的解集为Ф;命题乙:函数f (x)=(2a2-a) x在R上是增函数。分别求出符合下列条件的实数a的取值范围。
(1) 甲、乙中至少有一个是真命题;(2)甲、乙中有且仅有一个是真命题。
解:由甲命题为真,得(a-1)2-4a2<0, (3a-1)(a+1)>0,∴a< -1或a>,
由乙命题为真,得2a2-a>1, (2a+1)(a-1)>0,∴a< -或a>1。 ………4分
(1)若甲、乙全假,可得a∈[-,],故所求范围是(-∞, -)∪(, +∞) ………8分
(2)若甲、乙全真,可得a∈(-∞, -1)∪(1, +∞),故所求范围是[-1, -)∪(,1] ………12分
17.(12分)若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+。求证:a,b,c中至少有一个大于0。
解:假设a、b、c均不大于零,则a+b+c≤0 (*) ………2分
而由已知得,a+b+c=x2-2x+y2-2y+z2-2z+++=(x-1)2+(y-1)2+(z-1)2+π-3 ………8分
由于π-3<0,所以a+b+c>0,与(*)式矛盾,故假设错误,
所以,原命题成立。 ………12分
18.(12分)已知抛物线C:x2=2py(p>0)上一点A(m, 4)到其焦点F的距离为。
(1)求p与m的值;
(2)若直线l过焦点F交抛物线于P,Q两点,且|PQ|=5,求直线l的方程。
解:(1)依题=4+,∴p=,x2=y,∴m2=4,m=±2 ………5分
(2)依题可设PQ的方程为l:y=kx+,与x2=y联立,消去x,得y2-(+k2)y+=0,
∴y1+y2=+k2,而|PQ|= y1+y2+p=1+k2,k2=5-1=4,k=±2 ………10分
∴直线l的方程为y=2x+或y= -2x+, ………12分
19.(12分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点。
(1)求异面直线AC与PB的距离;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离。
答案:(1)、;(2)1;。
解析:以A为原点,以向量的方向为坐标轴方向建立空间直角坐标系,利用向量条件下的距离公式求解,以下省略。
20.(13分)如图,⊿BCD与⊿MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2。
(1)求直线AM与平面BCD所成角的大小;
(2)求平面ACM与平面BCD所成二面角的正弦值。
解:(1)取CD中点O,则MO⊥CD,
∵面MCD⊥面BCD交于CD,∴MO⊥面BCD,
又AB⊥面BCD,∴AB∥MO。
取AB中点F,连OF,由题设可知MO=,AF=,
∴OF∥AM,故OF与平面BCD所成的角等于所求的角。
而在Rt⊿BEF中,BO=,BF=,∠BOF=45 ,即所求的角为45 。 ………6分
(2)延长BO、AM相交于点G,∵MO∥AB且MO=AB,
∴OG=BO=,又CO=1,∴CG=2,作EH⊥CG于H,
由于ME⊥平面BCD,则MH⊥CG,∴∠MHO即为所求二面角的平面角。
在Rt⊿OCG中,由OH·CG=OC·OG,得OH=,
从而MH=,∴sin∠MHO=。 ………13分
另解:依题易知OB、OC、OM两两垂直,故可以如图建立空间直角坐标系,利用空间向量进行求解,过程略。
21、(14分)设椭圆C:的右焦点为F,过F的直线l与椭圆C相交于A、B两点,直线l的倾斜角为60 ,。
(1)求椭圆C的离心率;(2)如果|AB|=,求椭圆C的方程。
解:(1)设F(c, 0),则c2=a2-b2,且直线l的方程为y=(x-c),设A(x1, y1)、B(x2, y2),
由,得,∴y1+y2= -y2,y1y2=-2y22,
联立直线l与椭圆C的方程,并消元、整理,得,
于是 4a2=9c2,∴e=; ………7分
(2)∵|AB|=,∴ ①; 由e=,得5a2=9b2 ②,
联立①②解得a=3,b2=5,∴椭圆C的方程为 ………14分
马鞍山市第二中学2012—2013学年度
第一学期期终素质测试
高二数学试题(理科)
命题人 聂晓峰 审题人 张以虎
一、选择题(本大题共10小题,每小题5分,计50分)
1.命题“若a、b都是偶数,则a+b是偶数”的逆否命题是(▲▲)
A、若a+b不是偶数,则a、b都不是偶数 B、若a+b不是偶数,则a、b不都是偶数
C、若a、b都不是偶数,则a+b不是偶数 D、若a、b不都是偶数,则a+b不是偶数
2.“直线y=kx+1的倾斜角为钝角”的一个必要不充分条件是(▲▲)
A、k<0 B、k<-1 C、k<1 D、k>-2
3.下列语句为特称命题且为假命题的是(▲▲)
A、指数函数都是增函数 B、有一个事件的概率大于1吗?
C、有些三角形没有外接圆 D、存在一个实数x,使x2≤0
4.椭圆的焦点坐标为(▲▲)
A、(3, 0),(-3, 0) B、(0, 3),(0, -3) C、(2, 0),(-2, 0) D、(0, 2),(0, -2)
5.双曲线的渐近线方程为(▲▲)
A、y=±3x B、y=±x C、y=±x D、y=±x
6.过点(1, 1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有(▲▲)
A、1条 B、2条 C、3条 D、0条
7.已知S是⊿ABC所在平面外一点,D是SC的中点,若=x+y+z,则x+y+z的值为(▲▲)
A、0 B、1 C、2 D、3
8.若a、b、c为任意向量,λ∈R,下列等式不一定成立的是(▲▲)
A、(a+b)+c= a+(b+c) B、(a+b)·c= a·b+ a·c C、λ(a+b)=λa+λb D、(a·b)c= a(b·c)
9.已知A(x, 5-x, 2x-1),B(1, x+2, 2-x),当||取最小值时,x的值等于(▲▲)
A、 B、- C、19 D、
10.将正方形ABCD沿对角线AC折成直二面角,则异面直线AB与CD的夹角的余弦值是(▲▲)
A、- B、 C、 D、
二、填空题(本大题5小题,每小题5分,计25分)
11.在⊿ABC中,“A12.双曲线上一点P到右焦点的距离是实轴两端点到右焦点距离的等差中项,则点P到左焦点的距离为 ▲▲▲▲ ;
13.抛物线y=x2的焦点坐标是 ▲▲▲▲ ;
14.已知a=(1, 1, 0),b=(1, 1 ,1 ),若b=b1+b2,且b1∥a,b2⊥a,则b1=▲▲▲▲、b2=▲▲▲▲;
15.已知空间四边形ABCD的四条边和对角线长都为a,点E、F、G分别是AB,AD,DC的中点,则四个数量积①·;②·;③·;④·中,其中运算结果为的式子的序号为 ▲▲▲▲ ;
三、解答题(本大题共6小题,计75分)
16.(12分)给定两个命题:命题甲:关于x的不等式x 2 + (a-1)x +a2 ≤0的解集为Ф;命题乙:函数f (x)=(2a2-a) x在R上是增函数。分别求出符合下列条件的实数a的取值范围。
(1) 甲、乙中至少有一个是真命题;(2)甲、乙中有且仅有一个是真命题。
17.(12分)已知抛物线C:x2=2py(p>0)上一点A(m, 4)到其焦点F的距离为。
(1)求p与m的值;
(2)若直线l过焦点F交抛物线于P,Q两点,且|PQ|=5,求直线l的方程。
18.(12分)若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+。求证:a,b,c中至少有一个大于0。
19.(12分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点。
(1)求异面直线AC与PB的距离;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离。
20.(13分)如图,⊿BCD与⊿MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2。
(1)求直线AM与平面BCD所成角的大小;
(2)求平面ACM与平面BCD所成二面角的正弦值。
21、(14分)设椭圆C:的右焦点为F,过点F的直线l与椭圆C相交于A、B两点,直线l的倾斜角为60 ,且。
(1)求椭圆C的离心率;(2)如果|AB|=,求椭圆C的方程。
*******此页自行保存,只要上交答题卷,请将有关答案填入相应答题栏*******
2012-2013学年度第一学期期末考试高二数学理科***答题卷***
一、选择题(5×10=50)
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题(5×5=25)
11)、 ; 12)、 ; 13)、 ;
14)、 ; 15)、 。
三、解答题(本大题共6小题,计75分)
16.(12分)给定两个命题:命题甲:关于x的不等式x 2 + (a-1)x +a2 ≤0的解集为Ф;命题乙:函数f (x)=(2a2-a) x在R上是增函数。分别求出符合下列条件的实数a的取值范围。
(1) 甲、乙中至少有一个是真命题;(2)甲、乙中有且仅有一个是真命题。
17.(12分)若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+。求证:a,b,c中至少有一个大于0。
18.(12分)已知抛物线C:x2=2py(p>0)上一点A(m, 4)到其焦点F的距离为。
(1)求p与m的值;
(2)若直线l过焦点F交抛物线于P,Q两点,且|PQ|=5,求直线l的方程。
19.(12分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点。
(1)求异面直线AC与PB的距离;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离。
20.(13分)如图,⊿BCD与⊿MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2。
(1)求直线AM与平面BCD所成角的大小;
21、(14分)设椭圆C:的右焦点为F,过点F的直线l与椭圆C相交于A、B两点,直线l的倾斜角为60 ,。
(1)求椭圆C的离心率;
(2)如果|AB|=,求椭圆C的方程。
参考答案
一、选择题(3×12=36)
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C D B A A D A B
二、填空题(4×5=20)
11)、 充要条件 ; 12)、 13 ; 13)、 (0, 1) ;
14)、 (1, 1, 0) ; (0, 0, 1) ; 15)、 ②③ 。
三、解答题(本大题共6小题,计75分)
16.(12分)给定两个命题:命题甲:关于x的不等式x2 + (a-1)x +a2 ≤0的解集为Ф;命题乙:函数f (x)=(2a2-a) x在R上是增函数。分别求出符合下列条件的实数a的取值范围。
(1) 甲、乙中至少有一个是真命题;(2)甲、乙中有且仅有一个是真命题。
解:由甲命题为真,得(a-1)2-4a2<0, (3a-1)(a+1)>0,∴a< -1或a>,
由乙命题为真,得2a2-a>1, (2a+1)(a-1)>0,∴a< -或a>1。 ………4分
(1)若甲、乙全假,可得a∈[-,],故所求范围是(-∞, -)∪(, +∞) ………8分
(2)若甲、乙全真,可得a∈(-∞, -1)∪(1, +∞),故所求范围是[-1, -)∪(,1] ………12分
17.(12分)若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+。求证:a,b,c中至少有一个大于0。
解:假设a、b、c均不大于零,则a+b+c≤0 (*) ………2分
而由已知得,a+b+c=x2-2x+y2-2y+z2-2z+++=(x-1)2+(y-1)2+(z-1)2+π-3 ………8分
由于π-3<0,所以a+b+c>0,与(*)式矛盾,故假设错误,
所以,原命题成立。 ………12分
18.(12分)已知抛物线C:x2=2py(p>0)上一点A(m, 4)到其焦点F的距离为。
(1)求p与m的值;
(2)若直线l过焦点F交抛物线于P,Q两点,且|PQ|=5,求直线l的方程。
解:(1)依题=4+,∴p=,x2=y,∴m2=4,m=±2 ………5分
(2)依题可设PQ的方程为l:y=kx+,与x2=y联立,消去x,得y2-(+k2)y+=0,
∴y1+y2=+k2,而|PQ|= y1+y2+p=1+k2,k2=5-1=4,k=±2 ………10分
∴直线l的方程为y=2x+或y= -2x+, ………12分
19.(12分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点。
(1)求异面直线AC与PB的距离;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离。
答案:(1)、;(2)1;。
解析:以A为原点,以向量的方向为坐标轴方向建立空间直角坐标系,利用向量条件下的距离公式求解,以下省略。
20.(13分)如图,⊿BCD与⊿MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2。
(1)求直线AM与平面BCD所成角的大小;
(2)求平面ACM与平面BCD所成二面角的正弦值。
解:(1)取CD中点O,则MO⊥CD,
∵面MCD⊥面BCD交于CD,∴MO⊥面BCD,
又AB⊥面BCD,∴AB∥MO。
取AB中点F,连OF,由题设可知MO=,AF=,
∴OF∥AM,故OF与平面BCD所成的角等于所求的角。
而在Rt⊿BEF中,BO=,BF=,∠BOF=45 ,即所求的角为45 。 ………6分
(2)延长BO、AM相交于点G,∵MO∥AB且MO=AB,
∴OG=BO=,又CO=1,∴CG=2,作EH⊥CG于H,
由于ME⊥平面BCD,则MH⊥CG,∴∠MHO即为所求二面角的平面角。
在Rt⊿OCG中,由OH·CG=OC·OG,得OH=,
从而MH=,∴sin∠MHO=。 ………13分
另解:依题易知OB、OC、OM两两垂直,故可以如图建立空间直角坐标系,利用空间向量进行求解,过程略。
21、(14分)设椭圆C:的右焦点为F,过F的直线l与椭圆C相交于A、B两点,直线l的倾斜角为60 ,。
(1)求椭圆C的离心率;(2)如果|AB|=,求椭圆C的方程。
解:(1)设F(c, 0),则c2=a2-b2,且直线l的方程为y=(x-c),设A(x1, y1)、B(x2, y2),
由,得,∴y1+y2= -y2,y1y2=-2y22,
联立直线l与椭圆C的方程,并消元、整理,得,
于是 4a2=9c2,∴e=; ………7分
(2)∵|AB|=,∴ ①; 由e=,得5a2=9b2 ②,
联立①②解得a=3,b2=5,∴椭圆C的方程为 ………14分
D
C
B
A
第19题
C
P
D
B
A
E
M
第20题
E
A
B
D
P
C
第19题
A
B
C
D
M
第20题
E
A
B
D
P
C
第19题
z
A
B
C
D
M
O
x
y
F
G
H
第20题
E
A
B
D
P
C
第19题
A
B
C
D
M
第20题
E
A
B
D
P
C
第19题
A
B
C
D
M
第20题
E
A
B
D
P
C
第19题
z
A
B
C
D
M
O
x
y
F
G
H
第20题
E
A
B
D
P
C
第19题
A
B
C
D
M
第20题
E
A
B
D
P
C
第19题
A
B
C
D
M
第20题
E
A
B
D
P
C
第19题
z
A
B
C
D
M
O
x
y
F
G
H
第20题
PAGE
第一学期期终素质测试
高二数学试题(理科)
命题人 聂晓峰 审题人 张以虎
一、选择题(本大题共10小题,每小题5分,计50分)
1.命题“若a、b都是偶数,则a+b是偶数”的逆否命题是(▲▲)
A、若a+b不是偶数,则a、b都不是偶数 B、若a+b不是偶数,则a、b不都是偶数
C、若a、b都不是偶数,则a+b不是偶数 D、若a、b不都是偶数,则a+b不是偶数
2.“直线y=kx+1的倾斜角为钝角”的一个必要不充分条件是(▲▲)
A、k<0 B、k<-1 C、k<1 D、k>-2
3.下列语句为特称命题且为假命题的是(▲▲)
A、指数函数都是增函数 B、有一个事件的概率大于1吗?
C、有些三角形没有外接圆 D、存在一个实数x,使x2≤0
4.椭圆的焦点坐标为(▲▲)
A、(3, 0),(-3, 0) B、(0, 3),(0, -3) C、(2, 0),(-2, 0) D、(0, 2),(0, -2)
5.双曲线的渐近线方程为(▲▲)
A、y=±3x B、y=±x C、y=±x D、y=±x
6.过点(1, 1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有(▲▲)
A、1条 B、2条 C、3条 D、0条
7.已知S是⊿ABC所在平面外一点,D是SC的中点,若=x+y+z,则x+y+z的值为(▲▲)
A、0 B、1 C、2 D、3
8.若a、b、c为任意向量,λ∈R,下列等式不一定成立的是(▲▲)
A、(a+b)+c= a+(b+c) B、(a+b)·c= a·b+ a·c C、λ(a+b)=λa+λb D、(a·b)c= a(b·c)
9.已知A(x, 5-x, 2x-1),B(1, x+2, 2-x),当||取最小值时,x的值等于(▲▲)
A、 B、- C、19 D、
10.将正方形ABCD沿对角线AC折成直二面角,则异面直线AB与CD的夹角的余弦值是(▲▲)
A、- B、 C、 D、
二、填空题(本大题5小题,每小题5分,计25分)
11.在⊿ABC中,“A
13.抛物线y=x2的焦点坐标是 ▲▲▲▲ ;
14.已知a=(1, 1, 0),b=(1, 1 ,1 ),若b=b1+b2,且b1∥a,b2⊥a,则b1=▲▲▲▲、b2=▲▲▲▲;
15.已知空间四边形ABCD的四条边和对角线长都为a,点E、F、G分别是AB,AD,DC的中点,则四个数量积①·;②·;③·;④·中,其中运算结果为的式子的序号为 ▲▲▲▲ ;
三、解答题(本大题共6小题,计75分)
16.(12分)给定两个命题:命题甲:关于x的不等式x 2 + (a-1)x +a2 ≤0的解集为Ф;命题乙:函数f (x)=(2a2-a) x在R上是增函数。分别求出符合下列条件的实数a的取值范围。
(1) 甲、乙中至少有一个是真命题;(2)甲、乙中有且仅有一个是真命题。
17.(12分)已知抛物线C:x2=2py(p>0)上一点A(m, 4)到其焦点F的距离为。
(1)求p与m的值;
(2)若直线l过焦点F交抛物线于P,Q两点,且|PQ|=5,求直线l的方程。
18.(12分)若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+。求证:a,b,c中至少有一个大于0。
19.(12分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点。
(1)求异面直线AC与PB的距离;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离。
20.(13分)如图,⊿BCD与⊿MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2。
(1)求直线AM与平面BCD所成角的大小;
(2)求平面ACM与平面BCD所成二面角的正弦值。
21、(14分)设椭圆C:的右焦点为F,过点F的直线l与椭圆C相交于A、B两点,直线l的倾斜角为60 ,且。
(1)求椭圆C的离心率;(2)如果|AB|=,求椭圆C的方程。
*******此页自行保存,只要上交答题卷,请将有关答案填入相应答题栏*******
2012-2013学年度第一学期期末考试高二数学理科***答题卷***
一、选择题(5×10=50)
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题(5×5=25)
11)、 ; 12)、 ; 13)、 ;
14)、 ; 15)、 。
三、解答题(本大题共6小题,计75分)
16.(12分)给定两个命题:命题甲:关于x的不等式x 2 + (a-1)x +a2 ≤0的解集为Ф;命题乙:函数f (x)=(2a2-a) x在R上是增函数。分别求出符合下列条件的实数a的取值范围。
(1) 甲、乙中至少有一个是真命题;(2)甲、乙中有且仅有一个是真命题。
17.(12分)若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+。求证:a,b,c中至少有一个大于0。
18.(12分)已知抛物线C:x2=2py(p>0)上一点A(m, 4)到其焦点F的距离为。
(1)求p与m的值;
(2)若直线l过焦点F交抛物线于P,Q两点,且|PQ|=5,求直线l的方程。
19.(12分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点。
(1)求异面直线AC与PB的距离;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离。
20.(13分)如图,⊿BCD与⊿MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2。
(1)求直线AM与平面BCD所成角的大小;
21、(14分)设椭圆C:的右焦点为F,过点F的直线l与椭圆C相交于A、B两点,直线l的倾斜角为60 ,。
(1)求椭圆C的离心率;
(2)如果|AB|=,求椭圆C的方程。
参考答案
一、选择题(3×12=36)
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C D B A A D A B
二、填空题(4×5=20)
11)、 充要条件 ; 12)、 13 ; 13)、 (0, 1) ;
14)、 (1, 1, 0) ; (0, 0, 1) ; 15)、 ②③ 。
三、解答题(本大题共6小题,计75分)
16.(12分)给定两个命题:命题甲:关于x的不等式x2 + (a-1)x +a2 ≤0的解集为Ф;命题乙:函数f (x)=(2a2-a) x在R上是增函数。分别求出符合下列条件的实数a的取值范围。
(1) 甲、乙中至少有一个是真命题;(2)甲、乙中有且仅有一个是真命题。
解:由甲命题为真,得(a-1)2-4a2<0, (3a-1)(a+1)>0,∴a< -1或a>,
由乙命题为真,得2a2-a>1, (2a+1)(a-1)>0,∴a< -或a>1。 ………4分
(1)若甲、乙全假,可得a∈[-,],故所求范围是(-∞, -)∪(, +∞) ………8分
(2)若甲、乙全真,可得a∈(-∞, -1)∪(1, +∞),故所求范围是[-1, -)∪(,1] ………12分
17.(12分)若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+。求证:a,b,c中至少有一个大于0。
解:假设a、b、c均不大于零,则a+b+c≤0 (*) ………2分
而由已知得,a+b+c=x2-2x+y2-2y+z2-2z+++=(x-1)2+(y-1)2+(z-1)2+π-3 ………8分
由于π-3<0,所以a+b+c>0,与(*)式矛盾,故假设错误,
所以,原命题成立。 ………12分
18.(12分)已知抛物线C:x2=2py(p>0)上一点A(m, 4)到其焦点F的距离为。
(1)求p与m的值;
(2)若直线l过焦点F交抛物线于P,Q两点,且|PQ|=5,求直线l的方程。
解:(1)依题=4+,∴p=,x2=y,∴m2=4,m=±2 ………5分
(2)依题可设PQ的方程为l:y=kx+,与x2=y联立,消去x,得y2-(+k2)y+=0,
∴y1+y2=+k2,而|PQ|= y1+y2+p=1+k2,k2=5-1=4,k=±2 ………10分
∴直线l的方程为y=2x+或y= -2x+, ………12分
19.(12分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点。
(1)求异面直线AC与PB的距离;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离。
答案:(1)、;(2)1;。
解析:以A为原点,以向量的方向为坐标轴方向建立空间直角坐标系,利用向量条件下的距离公式求解,以下省略。
20.(13分)如图,⊿BCD与⊿MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2。
(1)求直线AM与平面BCD所成角的大小;
(2)求平面ACM与平面BCD所成二面角的正弦值。
解:(1)取CD中点O,则MO⊥CD,
∵面MCD⊥面BCD交于CD,∴MO⊥面BCD,
又AB⊥面BCD,∴AB∥MO。
取AB中点F,连OF,由题设可知MO=,AF=,
∴OF∥AM,故OF与平面BCD所成的角等于所求的角。
而在Rt⊿BEF中,BO=,BF=,∠BOF=45 ,即所求的角为45 。 ………6分
(2)延长BO、AM相交于点G,∵MO∥AB且MO=AB,
∴OG=BO=,又CO=1,∴CG=2,作EH⊥CG于H,
由于ME⊥平面BCD,则MH⊥CG,∴∠MHO即为所求二面角的平面角。
在Rt⊿OCG中,由OH·CG=OC·OG,得OH=,
从而MH=,∴sin∠MHO=。 ………13分
另解:依题易知OB、OC、OM两两垂直,故可以如图建立空间直角坐标系,利用空间向量进行求解,过程略。
21、(14分)设椭圆C:的右焦点为F,过F的直线l与椭圆C相交于A、B两点,直线l的倾斜角为60 ,。
(1)求椭圆C的离心率;(2)如果|AB|=,求椭圆C的方程。
解:(1)设F(c, 0),则c2=a2-b2,且直线l的方程为y=(x-c),设A(x1, y1)、B(x2, y2),
由,得,∴y1+y2= -y2,y1y2=-2y22,
联立直线l与椭圆C的方程,并消元、整理,得,
于是 4a2=9c2,∴e=; ………7分
(2)∵|AB|=,∴ ①; 由e=,得5a2=9b2 ②,
联立①②解得a=3,b2=5,∴椭圆C的方程为 ………14分
马鞍山市第二中学2012—2013学年度
第一学期期终素质测试
高二数学试题(理科)
命题人 聂晓峰 审题人 张以虎
一、选择题(本大题共10小题,每小题5分,计50分)
1.命题“若a、b都是偶数,则a+b是偶数”的逆否命题是(▲▲)
A、若a+b不是偶数,则a、b都不是偶数 B、若a+b不是偶数,则a、b不都是偶数
C、若a、b都不是偶数,则a+b不是偶数 D、若a、b不都是偶数,则a+b不是偶数
2.“直线y=kx+1的倾斜角为钝角”的一个必要不充分条件是(▲▲)
A、k<0 B、k<-1 C、k<1 D、k>-2
3.下列语句为特称命题且为假命题的是(▲▲)
A、指数函数都是增函数 B、有一个事件的概率大于1吗?
C、有些三角形没有外接圆 D、存在一个实数x,使x2≤0
4.椭圆的焦点坐标为(▲▲)
A、(3, 0),(-3, 0) B、(0, 3),(0, -3) C、(2, 0),(-2, 0) D、(0, 2),(0, -2)
5.双曲线的渐近线方程为(▲▲)
A、y=±3x B、y=±x C、y=±x D、y=±x
6.过点(1, 1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有(▲▲)
A、1条 B、2条 C、3条 D、0条
7.已知S是⊿ABC所在平面外一点,D是SC的中点,若=x+y+z,则x+y+z的值为(▲▲)
A、0 B、1 C、2 D、3
8.若a、b、c为任意向量,λ∈R,下列等式不一定成立的是(▲▲)
A、(a+b)+c= a+(b+c) B、(a+b)·c= a·b+ a·c C、λ(a+b)=λa+λb D、(a·b)c= a(b·c)
9.已知A(x, 5-x, 2x-1),B(1, x+2, 2-x),当||取最小值时,x的值等于(▲▲)
A、 B、- C、19 D、
10.将正方形ABCD沿对角线AC折成直二面角,则异面直线AB与CD的夹角的余弦值是(▲▲)
A、- B、 C、 D、
二、填空题(本大题5小题,每小题5分,计25分)
11.在⊿ABC中,“A
13.抛物线y=x2的焦点坐标是 ▲▲▲▲ ;
14.已知a=(1, 1, 0),b=(1, 1 ,1 ),若b=b1+b2,且b1∥a,b2⊥a,则b1=▲▲▲▲、b2=▲▲▲▲;
15.已知空间四边形ABCD的四条边和对角线长都为a,点E、F、G分别是AB,AD,DC的中点,则四个数量积①·;②·;③·;④·中,其中运算结果为的式子的序号为 ▲▲▲▲ ;
三、解答题(本大题共6小题,计75分)
16.(12分)给定两个命题:命题甲:关于x的不等式x 2 + (a-1)x +a2 ≤0的解集为Ф;命题乙:函数f (x)=(2a2-a) x在R上是增函数。分别求出符合下列条件的实数a的取值范围。
(1) 甲、乙中至少有一个是真命题;(2)甲、乙中有且仅有一个是真命题。
17.(12分)已知抛物线C:x2=2py(p>0)上一点A(m, 4)到其焦点F的距离为。
(1)求p与m的值;
(2)若直线l过焦点F交抛物线于P,Q两点,且|PQ|=5,求直线l的方程。
18.(12分)若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+。求证:a,b,c中至少有一个大于0。
19.(12分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点。
(1)求异面直线AC与PB的距离;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离。
20.(13分)如图,⊿BCD与⊿MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2。
(1)求直线AM与平面BCD所成角的大小;
(2)求平面ACM与平面BCD所成二面角的正弦值。
21、(14分)设椭圆C:的右焦点为F,过点F的直线l与椭圆C相交于A、B两点,直线l的倾斜角为60 ,且。
(1)求椭圆C的离心率;(2)如果|AB|=,求椭圆C的方程。
*******此页自行保存,只要上交答题卷,请将有关答案填入相应答题栏*******
2012-2013学年度第一学期期末考试高二数学理科***答题卷***
一、选择题(5×10=50)
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题(5×5=25)
11)、 ; 12)、 ; 13)、 ;
14)、 ; 15)、 。
三、解答题(本大题共6小题,计75分)
16.(12分)给定两个命题:命题甲:关于x的不等式x 2 + (a-1)x +a2 ≤0的解集为Ф;命题乙:函数f (x)=(2a2-a) x在R上是增函数。分别求出符合下列条件的实数a的取值范围。
(1) 甲、乙中至少有一个是真命题;(2)甲、乙中有且仅有一个是真命题。
17.(12分)若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+。求证:a,b,c中至少有一个大于0。
18.(12分)已知抛物线C:x2=2py(p>0)上一点A(m, 4)到其焦点F的距离为。
(1)求p与m的值;
(2)若直线l过焦点F交抛物线于P,Q两点,且|PQ|=5,求直线l的方程。
19.(12分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点。
(1)求异面直线AC与PB的距离;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离。
20.(13分)如图,⊿BCD与⊿MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2。
(1)求直线AM与平面BCD所成角的大小;
21、(14分)设椭圆C:的右焦点为F,过点F的直线l与椭圆C相交于A、B两点,直线l的倾斜角为60 ,。
(1)求椭圆C的离心率;
(2)如果|AB|=,求椭圆C的方程。
参考答案
一、选择题(3×12=36)
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C D B A A D A B
二、填空题(4×5=20)
11)、 充要条件 ; 12)、 13 ; 13)、 (0, 1) ;
14)、 (1, 1, 0) ; (0, 0, 1) ; 15)、 ②③ 。
三、解答题(本大题共6小题,计75分)
16.(12分)给定两个命题:命题甲:关于x的不等式x2 + (a-1)x +a2 ≤0的解集为Ф;命题乙:函数f (x)=(2a2-a) x在R上是增函数。分别求出符合下列条件的实数a的取值范围。
(1) 甲、乙中至少有一个是真命题;(2)甲、乙中有且仅有一个是真命题。
解:由甲命题为真,得(a-1)2-4a2<0, (3a-1)(a+1)>0,∴a< -1或a>,
由乙命题为真,得2a2-a>1, (2a+1)(a-1)>0,∴a< -或a>1。 ………4分
(1)若甲、乙全假,可得a∈[-,],故所求范围是(-∞, -)∪(, +∞) ………8分
(2)若甲、乙全真,可得a∈(-∞, -1)∪(1, +∞),故所求范围是[-1, -)∪(,1] ………12分
17.(12分)若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+。求证:a,b,c中至少有一个大于0。
解:假设a、b、c均不大于零,则a+b+c≤0 (*) ………2分
而由已知得,a+b+c=x2-2x+y2-2y+z2-2z+++=(x-1)2+(y-1)2+(z-1)2+π-3 ………8分
由于π-3<0,所以a+b+c>0,与(*)式矛盾,故假设错误,
所以,原命题成立。 ………12分
18.(12分)已知抛物线C:x2=2py(p>0)上一点A(m, 4)到其焦点F的距离为。
(1)求p与m的值;
(2)若直线l过焦点F交抛物线于P,Q两点,且|PQ|=5,求直线l的方程。
解:(1)依题=4+,∴p=,x2=y,∴m2=4,m=±2 ………5分
(2)依题可设PQ的方程为l:y=kx+,与x2=y联立,消去x,得y2-(+k2)y+=0,
∴y1+y2=+k2,而|PQ|= y1+y2+p=1+k2,k2=5-1=4,k=±2 ………10分
∴直线l的方程为y=2x+或y= -2x+, ………12分
19.(12分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点。
(1)求异面直线AC与PB的距离;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离。
答案:(1)、;(2)1;。
解析:以A为原点,以向量的方向为坐标轴方向建立空间直角坐标系,利用向量条件下的距离公式求解,以下省略。
20.(13分)如图,⊿BCD与⊿MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2。
(1)求直线AM与平面BCD所成角的大小;
(2)求平面ACM与平面BCD所成二面角的正弦值。
解:(1)取CD中点O,则MO⊥CD,
∵面MCD⊥面BCD交于CD,∴MO⊥面BCD,
又AB⊥面BCD,∴AB∥MO。
取AB中点F,连OF,由题设可知MO=,AF=,
∴OF∥AM,故OF与平面BCD所成的角等于所求的角。
而在Rt⊿BEF中,BO=,BF=,∠BOF=45 ,即所求的角为45 。 ………6分
(2)延长BO、AM相交于点G,∵MO∥AB且MO=AB,
∴OG=BO=,又CO=1,∴CG=2,作EH⊥CG于H,
由于ME⊥平面BCD,则MH⊥CG,∴∠MHO即为所求二面角的平面角。
在Rt⊿OCG中,由OH·CG=OC·OG,得OH=,
从而MH=,∴sin∠MHO=。 ………13分
另解:依题易知OB、OC、OM两两垂直,故可以如图建立空间直角坐标系,利用空间向量进行求解,过程略。
21、(14分)设椭圆C:的右焦点为F,过F的直线l与椭圆C相交于A、B两点,直线l的倾斜角为60 ,。
(1)求椭圆C的离心率;(2)如果|AB|=,求椭圆C的方程。
解:(1)设F(c, 0),则c2=a2-b2,且直线l的方程为y=(x-c),设A(x1, y1)、B(x2, y2),
由,得,∴y1+y2= -y2,y1y2=-2y22,
联立直线l与椭圆C的方程,并消元、整理,得,
于是 4a2=9c2,∴e=; ………7分
(2)∵|AB|=,∴ ①; 由e=,得5a2=9b2 ②,
联立①②解得a=3,b2=5,∴椭圆C的方程为 ………14分
马鞍山市第二中学2012—2013学年度
第一学期期终素质测试
高二数学试题(理科)
命题人 聂晓峰 审题人 张以虎
一、选择题(本大题共10小题,每小题5分,计50分)
1.命题“若a、b都是偶数,则a+b是偶数”的逆否命题是(▲▲)
A、若a+b不是偶数,则a、b都不是偶数 B、若a+b不是偶数,则a、b不都是偶数
C、若a、b都不是偶数,则a+b不是偶数 D、若a、b不都是偶数,则a+b不是偶数
2.“直线y=kx+1的倾斜角为钝角”的一个必要不充分条件是(▲▲)
A、k<0 B、k<-1 C、k<1 D、k>-2
3.下列语句为特称命题且为假命题的是(▲▲)
A、指数函数都是增函数 B、有一个事件的概率大于1吗?
C、有些三角形没有外接圆 D、存在一个实数x,使x2≤0
4.椭圆的焦点坐标为(▲▲)
A、(3, 0),(-3, 0) B、(0, 3),(0, -3) C、(2, 0),(-2, 0) D、(0, 2),(0, -2)
5.双曲线的渐近线方程为(▲▲)
A、y=±3x B、y=±x C、y=±x D、y=±x
6.过点(1, 1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有(▲▲)
A、1条 B、2条 C、3条 D、0条
7.已知S是⊿ABC所在平面外一点,D是SC的中点,若=x+y+z,则x+y+z的值为(▲▲)
A、0 B、1 C、2 D、3
8.若a、b、c为任意向量,λ∈R,下列等式不一定成立的是(▲▲)
A、(a+b)+c= a+(b+c) B、(a+b)·c= a·b+ a·c C、λ(a+b)=λa+λb D、(a·b)c= a(b·c)
9.已知A(x, 5-x, 2x-1),B(1, x+2, 2-x),当||取最小值时,x的值等于(▲▲)
A、 B、- C、19 D、
10.将正方形ABCD沿对角线AC折成直二面角,则异面直线AB与CD的夹角的余弦值是(▲▲)
A、- B、 C、 D、
二、填空题(本大题5小题,每小题5分,计25分)
11.在⊿ABC中,“A
13.抛物线y=x2的焦点坐标是 ▲▲▲▲ ;
14.已知a=(1, 1, 0),b=(1, 1 ,1 ),若b=b1+b2,且b1∥a,b2⊥a,则b1=▲▲▲▲、b2=▲▲▲▲;
15.已知空间四边形ABCD的四条边和对角线长都为a,点E、F、G分别是AB,AD,DC的中点,则四个数量积①·;②·;③·;④·中,其中运算结果为的式子的序号为 ▲▲▲▲ ;
三、解答题(本大题共6小题,计75分)
16.(12分)给定两个命题:命题甲:关于x的不等式x 2 + (a-1)x +a2 ≤0的解集为Ф;命题乙:函数f (x)=(2a2-a) x在R上是增函数。分别求出符合下列条件的实数a的取值范围。
(1) 甲、乙中至少有一个是真命题;(2)甲、乙中有且仅有一个是真命题。
17.(12分)已知抛物线C:x2=2py(p>0)上一点A(m, 4)到其焦点F的距离为。
(1)求p与m的值;
(2)若直线l过焦点F交抛物线于P,Q两点,且|PQ|=5,求直线l的方程。
18.(12分)若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+。求证:a,b,c中至少有一个大于0。
19.(12分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点。
(1)求异面直线AC与PB的距离;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离。
20.(13分)如图,⊿BCD与⊿MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2。
(1)求直线AM与平面BCD所成角的大小;
(2)求平面ACM与平面BCD所成二面角的正弦值。
21、(14分)设椭圆C:的右焦点为F,过点F的直线l与椭圆C相交于A、B两点,直线l的倾斜角为60 ,且。
(1)求椭圆C的离心率;(2)如果|AB|=,求椭圆C的方程。
*******此页自行保存,只要上交答题卷,请将有关答案填入相应答题栏*******
2012-2013学年度第一学期期末考试高二数学理科***答题卷***
一、选择题(5×10=50)
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题(5×5=25)
11)、 ; 12)、 ; 13)、 ;
14)、 ; 15)、 。
三、解答题(本大题共6小题,计75分)
16.(12分)给定两个命题:命题甲:关于x的不等式x 2 + (a-1)x +a2 ≤0的解集为Ф;命题乙:函数f (x)=(2a2-a) x在R上是增函数。分别求出符合下列条件的实数a的取值范围。
(1) 甲、乙中至少有一个是真命题;(2)甲、乙中有且仅有一个是真命题。
17.(12分)若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+。求证:a,b,c中至少有一个大于0。
18.(12分)已知抛物线C:x2=2py(p>0)上一点A(m, 4)到其焦点F的距离为。
(1)求p与m的值;
(2)若直线l过焦点F交抛物线于P,Q两点,且|PQ|=5,求直线l的方程。
19.(12分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点。
(1)求异面直线AC与PB的距离;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离。
20.(13分)如图,⊿BCD与⊿MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2。
(1)求直线AM与平面BCD所成角的大小;
21、(14分)设椭圆C:的右焦点为F,过点F的直线l与椭圆C相交于A、B两点,直线l的倾斜角为60 ,。
(1)求椭圆C的离心率;
(2)如果|AB|=,求椭圆C的方程。
参考答案
一、选择题(3×12=36)
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C D B A A D A B
二、填空题(4×5=20)
11)、 充要条件 ; 12)、 13 ; 13)、 (0, 1) ;
14)、 (1, 1, 0) ; (0, 0, 1) ; 15)、 ②③ 。
三、解答题(本大题共6小题,计75分)
16.(12分)给定两个命题:命题甲:关于x的不等式x2 + (a-1)x +a2 ≤0的解集为Ф;命题乙:函数f (x)=(2a2-a) x在R上是增函数。分别求出符合下列条件的实数a的取值范围。
(1) 甲、乙中至少有一个是真命题;(2)甲、乙中有且仅有一个是真命题。
解:由甲命题为真,得(a-1)2-4a2<0, (3a-1)(a+1)>0,∴a< -1或a>,
由乙命题为真,得2a2-a>1, (2a+1)(a-1)>0,∴a< -或a>1。 ………4分
(1)若甲、乙全假,可得a∈[-,],故所求范围是(-∞, -)∪(, +∞) ………8分
(2)若甲、乙全真,可得a∈(-∞, -1)∪(1, +∞),故所求范围是[-1, -)∪(,1] ………12分
17.(12分)若a、b、c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+。求证:a,b,c中至少有一个大于0。
解:假设a、b、c均不大于零,则a+b+c≤0 (*) ………2分
而由已知得,a+b+c=x2-2x+y2-2y+z2-2z+++=(x-1)2+(y-1)2+(z-1)2+π-3 ………8分
由于π-3<0,所以a+b+c>0,与(*)式矛盾,故假设错误,
所以,原命题成立。 ………12分
18.(12分)已知抛物线C:x2=2py(p>0)上一点A(m, 4)到其焦点F的距离为。
(1)求p与m的值;
(2)若直线l过焦点F交抛物线于P,Q两点,且|PQ|=5,求直线l的方程。
解:(1)依题=4+,∴p=,x2=y,∴m2=4,m=±2 ………5分
(2)依题可设PQ的方程为l:y=kx+,与x2=y联立,消去x,得y2-(+k2)y+=0,
∴y1+y2=+k2,而|PQ|= y1+y2+p=1+k2,k2=5-1=4,k=±2 ………10分
∴直线l的方程为y=2x+或y= -2x+, ………12分
19.(12分)如图,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点。
(1)求异面直线AC与PB的距离;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离。
答案:(1)、;(2)1;。
解析:以A为原点,以向量的方向为坐标轴方向建立空间直角坐标系,利用向量条件下的距离公式求解,以下省略。
20.(13分)如图,⊿BCD与⊿MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2。
(1)求直线AM与平面BCD所成角的大小;
(2)求平面ACM与平面BCD所成二面角的正弦值。
解:(1)取CD中点O,则MO⊥CD,
∵面MCD⊥面BCD交于CD,∴MO⊥面BCD,
又AB⊥面BCD,∴AB∥MO。
取AB中点F,连OF,由题设可知MO=,AF=,
∴OF∥AM,故OF与平面BCD所成的角等于所求的角。
而在Rt⊿BEF中,BO=,BF=,∠BOF=45 ,即所求的角为45 。 ………6分
(2)延长BO、AM相交于点G,∵MO∥AB且MO=AB,
∴OG=BO=,又CO=1,∴CG=2,作EH⊥CG于H,
由于ME⊥平面BCD,则MH⊥CG,∴∠MHO即为所求二面角的平面角。
在Rt⊿OCG中,由OH·CG=OC·OG,得OH=,
从而MH=,∴sin∠MHO=。 ………13分
另解:依题易知OB、OC、OM两两垂直,故可以如图建立空间直角坐标系,利用空间向量进行求解,过程略。
21、(14分)设椭圆C:的右焦点为F,过F的直线l与椭圆C相交于A、B两点,直线l的倾斜角为60 ,。
(1)求椭圆C的离心率;(2)如果|AB|=,求椭圆C的方程。
解:(1)设F(c, 0),则c2=a2-b2,且直线l的方程为y=(x-c),设A(x1, y1)、B(x2, y2),
由,得,∴y1+y2= -y2,y1y2=-2y22,
联立直线l与椭圆C的方程,并消元、整理,得,
于是 4a2=9c2,∴e=; ………7分
(2)∵|AB|=,∴ ①; 由e=,得5a2=9b2 ②,
联立①②解得a=3,b2=5,∴椭圆C的方程为 ………14分
D
C
B
A
第19题
C
P
D
B
A
E
M
第20题
E
A
B
D
P
C
第19题
A
B
C
D
M
第20题
E
A
B
D
P
C
第19题
z
A
B
C
D
M
O
x
y
F
G
H
第20题
E
A
B
D
P
C
第19题
A
B
C
D
M
第20题
E
A
B
D
P
C
第19题
A
B
C
D
M
第20题
E
A
B
D
P
C
第19题
z
A
B
C
D
M
O
x
y
F
G
H
第20题
E
A
B
D
P
C
第19题
A
B
C
D
M
第20题
E
A
B
D
P
C
第19题
A
B
C
D
M
第20题
E
A
B
D
P
C
第19题
z
A
B
C
D
M
O
x
y
F
G
H
第20题
PAGE
同课章节目录
