七年级数学冀教版下册 6.2二元一次方程组解法 学案(无答案)
文档属性
| 名称 | 七年级数学冀教版下册 6.2二元一次方程组解法 学案(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 266.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-13 13:44:40 | ||
图片预览


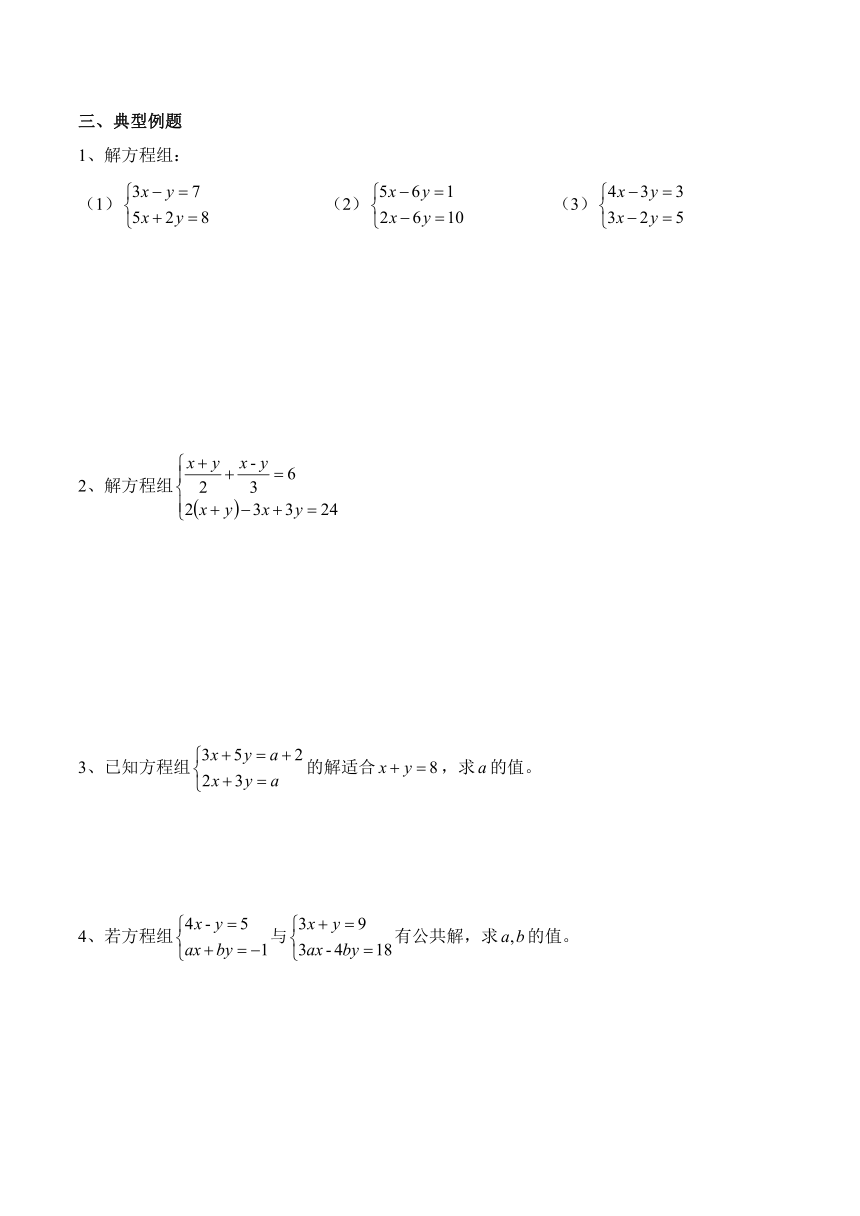

文档简介
第二讲 二元一次方程组的解法
一、教学目标
1、通过探索,领会并掌握解二元一次方程组的方法,根据方程组的情况,能恰当地运用“代入消元法”和“加减消元法”解方程组。
2、体会二元一次方程组中的“消元”思想,即通过消元把解二元一次方程组转化成解一元一次方程。由此感受“转化思想”的广泛应用。
二、知识点梳理
知识点一、用含一个未知数的代数式表示另一个未知数
用含一个未知数的代数式表示另一个未知数是代入消元法的基础,它是代入消元法的第一步。
例1、把下列各式用含的代数式表示.
(1);(2);(3);(4)。
知识点二、用代入消元法解二元一次方程组
将方程组中一个方程的某个未知数用含有另一个未知数的代数式表示出来,代入领一个方程中,消去一个未知数,得到一元一次方程,通过解一元一次方程求得方程组的解。这种解方程的方法叫做代入消元法,简称代入法。
用代入消元法解一元二次方程在的一般步骤:
从方程组中选定一个系数比较简单的方程进行变形,用含有(或)的代数式表示(或),即变成(或)的形式;
将(或)代入另一个方程中,消去(或),得到一个关于(或)的一元一次方程;
解这个一元一次方程,求出(或)的值;
把(或)的值代入(或)中,求出(或)的值;
把求得的的值用“{”联立起来就是方程组的解。
例2、解方程组
知识点三、用加减消元法解二元一次方程组
通过将方程组中两个方程相加(或相减)消去一个未知数,得到一元一次方程,最后求得方程组的解,这种解方程组的方法叫做加减消元法,简称加减法。用加减消元法解二元一次方程组的一般步骤:
把一个方程或两个方程的两边乘适当的数,使方程组的两个方程中的某一个未知数的系数互为相反数或相等;
把变形后的两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;
解这个一元一次方程,求得一个未知数的值;
把求得的未知数的值代入到原方程组中未知系数比较简单的一个方程中,求出另一个未知数的值,从而得到方程组的解;
最后检验求得的结果是否正确。
以上步骤可以简单概括为:变换系数→加减消元→回代求解→检验结果。
例3、解方程组
三、典型例题
1、解方程组:
(1) (2) (3)
解方程组
已知方程组的解适合,求的值。
若方程组与有公共解,求的值。
如图,点O在直线AB上,OC为射线,∠1比∠2的3倍少10°,求∠1,∠2的度数。
6、若关于的方程组的解的和是2,求。
四、课堂练习
1、对于方程用含的代数式表示的式子为( )
A、 B、 C、 D、
用代入法解方程:
(1) (2)
(3) (4)
(5) (6)
利用加减消元法解方程组下列做法正确的是( )
A、要消去,可以将①×5+②×2 B、要消去,可以将①×3+②×(-5)
C、要消去,可以将①×5+②×3 D、要消去,可以将①×(-5)+②×2
已知方程组当利用代入法消去后得到的方程是( )
A、 B、 C、 D、
用加减法解方程组时,有下列四种变形,其中正确的是( )
A、 B、 C、 D、
若方程组可直接用加减法消去,则的关系为( )
A、互为相反数 B、互为倒数 C、绝对值相等 D、相等
已知,那么的值是( )
A、-1 B、0 C、1 D、2
已知,求的值。
已知是二元一次方程组的解,求的值。
有大小两种船,1艘大船与4艘小船一次可以载乘客46人,2艘大船与3艘小船一次可以载乘客57人。某船家有3艘大船与6艘小船,一次性可以载乘客的人数为( )
A、129 B、120 C、108 D、96
用加减法解方程组:
(1) (2)
解方程:
(1) (2)
(3) (4)
(5) (6)
五、课后作业
1、用加减法解方程组,可将方程①两边同乘__________,再与方程②相________.
2、已知互为相反数,并且,则=______________.
3、解方程组时,比较好的解法是( )
A、由①得,再代入② B、由②得,再代入①
C、由②-①,消去 D、由①×2+②,消去
若,则的值为( )
A、 B、 C、 D、
若满足方程组,则的值等于( )
A、-1 B、1 C、2 D、3
在代数式中,当时,它的值为-5;当时,它的值为3,则=_____,=_____。
解方程组:
(1) (2) (3)
一、教学目标
1、通过探索,领会并掌握解二元一次方程组的方法,根据方程组的情况,能恰当地运用“代入消元法”和“加减消元法”解方程组。
2、体会二元一次方程组中的“消元”思想,即通过消元把解二元一次方程组转化成解一元一次方程。由此感受“转化思想”的广泛应用。
二、知识点梳理
知识点一、用含一个未知数的代数式表示另一个未知数
用含一个未知数的代数式表示另一个未知数是代入消元法的基础,它是代入消元法的第一步。
例1、把下列各式用含的代数式表示.
(1);(2);(3);(4)。
知识点二、用代入消元法解二元一次方程组
将方程组中一个方程的某个未知数用含有另一个未知数的代数式表示出来,代入领一个方程中,消去一个未知数,得到一元一次方程,通过解一元一次方程求得方程组的解。这种解方程的方法叫做代入消元法,简称代入法。
用代入消元法解一元二次方程在的一般步骤:
从方程组中选定一个系数比较简单的方程进行变形,用含有(或)的代数式表示(或),即变成(或)的形式;
将(或)代入另一个方程中,消去(或),得到一个关于(或)的一元一次方程;
解这个一元一次方程,求出(或)的值;
把(或)的值代入(或)中,求出(或)的值;
把求得的的值用“{”联立起来就是方程组的解。
例2、解方程组
知识点三、用加减消元法解二元一次方程组
通过将方程组中两个方程相加(或相减)消去一个未知数,得到一元一次方程,最后求得方程组的解,这种解方程组的方法叫做加减消元法,简称加减法。用加减消元法解二元一次方程组的一般步骤:
把一个方程或两个方程的两边乘适当的数,使方程组的两个方程中的某一个未知数的系数互为相反数或相等;
把变形后的两个方程的两边分别相加或相减,消去一个未知数,得到一个一元一次方程;
解这个一元一次方程,求得一个未知数的值;
把求得的未知数的值代入到原方程组中未知系数比较简单的一个方程中,求出另一个未知数的值,从而得到方程组的解;
最后检验求得的结果是否正确。
以上步骤可以简单概括为:变换系数→加减消元→回代求解→检验结果。
例3、解方程组
三、典型例题
1、解方程组:
(1) (2) (3)
解方程组
已知方程组的解适合,求的值。
若方程组与有公共解,求的值。
如图,点O在直线AB上,OC为射线,∠1比∠2的3倍少10°,求∠1,∠2的度数。
6、若关于的方程组的解的和是2,求。
四、课堂练习
1、对于方程用含的代数式表示的式子为( )
A、 B、 C、 D、
用代入法解方程:
(1) (2)
(3) (4)
(5) (6)
利用加减消元法解方程组下列做法正确的是( )
A、要消去,可以将①×5+②×2 B、要消去,可以将①×3+②×(-5)
C、要消去,可以将①×5+②×3 D、要消去,可以将①×(-5)+②×2
已知方程组当利用代入法消去后得到的方程是( )
A、 B、 C、 D、
用加减法解方程组时,有下列四种变形,其中正确的是( )
A、 B、 C、 D、
若方程组可直接用加减法消去,则的关系为( )
A、互为相反数 B、互为倒数 C、绝对值相等 D、相等
已知,那么的值是( )
A、-1 B、0 C、1 D、2
已知,求的值。
已知是二元一次方程组的解,求的值。
有大小两种船,1艘大船与4艘小船一次可以载乘客46人,2艘大船与3艘小船一次可以载乘客57人。某船家有3艘大船与6艘小船,一次性可以载乘客的人数为( )
A、129 B、120 C、108 D、96
用加减法解方程组:
(1) (2)
解方程:
(1) (2)
(3) (4)
(5) (6)
五、课后作业
1、用加减法解方程组,可将方程①两边同乘__________,再与方程②相________.
2、已知互为相反数,并且,则=______________.
3、解方程组时,比较好的解法是( )
A、由①得,再代入② B、由②得,再代入①
C、由②-①,消去 D、由①×2+②,消去
若,则的值为( )
A、 B、 C、 D、
若满足方程组,则的值等于( )
A、-1 B、1 C、2 D、3
在代数式中,当时,它的值为-5;当时,它的值为3,则=_____,=_____。
解方程组:
(1) (2) (3)
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
