3.4宇宙速度与航天课件 (21张PPT)
文档属性
| 名称 | 3.4宇宙速度与航天课件 (21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-13 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
第三章 第四节 宇宙速度与航天
问题1.为什么抛出小球最终都落地?
问题2.为什么抛出小球落地距离不同?
问题3.若抛出物体的水平初速度足够大,物体 将会怎样
问题5:以多大的速度在地面附近发射这个物体,物体刚好不落回地面,成为绕地球表面做匀速圆周运动的卫星 ?
问题4: 为什么牛顿关于卫星的设想很长时间都未能实现?
知识回顾:
汽车过拱桥
牛顿设想:抛出速度很大时,物体就不会落回地面,它将绕地球运动,成为人造卫星。
地球
物体绕地球做匀速圆周运动时,地球的万有引力提供其做圆周运动的向心力。
探究:
已知:地球质量M,物体质量m,物体到地心的距离为r。
求:物体恰好在地球表面附近绕地球匀速圆周运动的速度v。
地球
第一宇宙速度
当卫星近地环绕时,可认为轨道半径r等于地球半径,将:
r=6400km, G=6.67X10-11N m2/kg2, M=5.98X1024kg, 代入得:
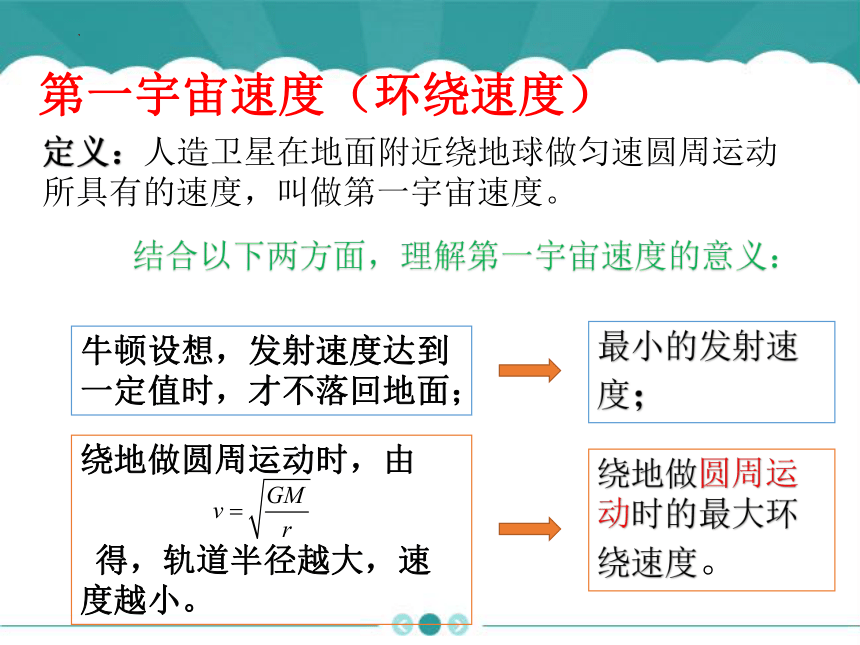
第一宇宙速度(环绕速度)
绕地做圆周运动时,由
得,轨道半径越大,速度越小。
定义:人造卫星在地面附近绕地球做匀速圆周运动所具有的速度,叫做第一宇宙速度。
结合以下两方面,理解第一宇宙速度的意义:
牛顿设想,发射速度达到一定值时,才不落回地面;
最小的发射速度;
绕地做圆周运动时的最大环绕速度。
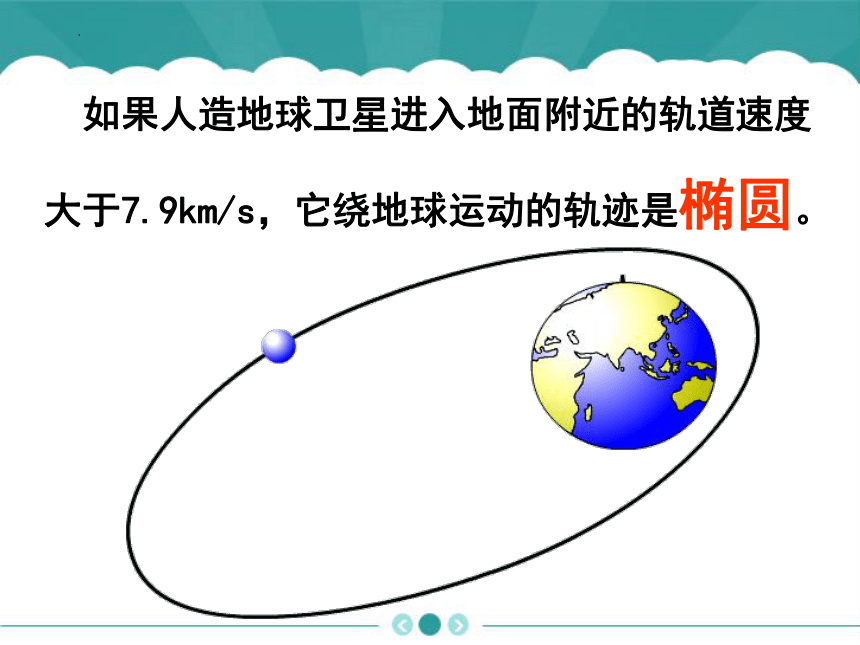
问题6:如果发射速度大于7.9km/s,会怎样?
如果人造地球卫星进入地面附近的轨道速度大于7.9km/s,它绕地球运动的轨迹是椭圆。
第二宇宙速度:
当卫星的速度等于或大于11.2km/s时,卫星就会脱离地球的引力,不再绕地球运行。这个速度叫第二宇宙速度。
第三宇宙速度:如果物体的速度等于或大于16.7km/s,物体就摆脱了太阳引力的束缚,飞到太阳系以外的宇宙空间去。这个速度叫第三宇宙速度。
V1=7.9km/s
地球
V2=11.2km/s
V3=16.7km/s
【问题探究3】卫星运行时,其向心加速度、线速度、角速度、周期,分别与其轨道半径的关系。
项目 推导式 关系式 结论
v与r的关系
ω与r的关系
T与r的关系
a与r的关系
【结论】高轨,低速,大周期,小加速度。
r越大 ω越小
r越大 T越大
r越大 a越小
r越大 v越小
1、 我国发射的一颗绕月运行的探月卫星“嫦娥1号”,设该卫星的轨道是圆形的,且贴近月球表面.已知月球的质量约为地球质量的 ,月球的半径约为地球半径的 ,地球上的第一宇宙速度约为7.9 km/s,则该探月卫星绕月运行的速率约为( )
A、0.4 km/s B、1.8 km/s
C、11 km/s D、36 km/s
√
√
地球同步卫星
所谓地球同步卫星,是相对于地面静止的和地球具有相同周期的卫星,同步卫星必须位于赤道平面内,且到地面的高度一定。
r v w T a
“全部固定”
T=1天=86400秒
h=36000Km
V=3.07Km/s
F引>F向
F引v1、v2、v3、v4,四个速度的大小依次如何?
距离地球5500万光年
质量约为太阳的65亿倍
第三章 第四节 宇宙速度与航天
问题1.为什么抛出小球最终都落地?
问题2.为什么抛出小球落地距离不同?
问题3.若抛出物体的水平初速度足够大,物体 将会怎样
问题5:以多大的速度在地面附近发射这个物体,物体刚好不落回地面,成为绕地球表面做匀速圆周运动的卫星 ?
问题4: 为什么牛顿关于卫星的设想很长时间都未能实现?
知识回顾:
汽车过拱桥
牛顿设想:抛出速度很大时,物体就不会落回地面,它将绕地球运动,成为人造卫星。
地球
物体绕地球做匀速圆周运动时,地球的万有引力提供其做圆周运动的向心力。
探究:
已知:地球质量M,物体质量m,物体到地心的距离为r。
求:物体恰好在地球表面附近绕地球匀速圆周运动的速度v。
地球
第一宇宙速度
当卫星近地环绕时,可认为轨道半径r等于地球半径,将:
r=6400km, G=6.67X10-11N m2/kg2, M=5.98X1024kg, 代入得:
第一宇宙速度(环绕速度)
绕地做圆周运动时,由
得,轨道半径越大,速度越小。
定义:人造卫星在地面附近绕地球做匀速圆周运动所具有的速度,叫做第一宇宙速度。
结合以下两方面,理解第一宇宙速度的意义:
牛顿设想,发射速度达到一定值时,才不落回地面;
最小的发射速度;
绕地做圆周运动时的最大环绕速度。
问题6:如果发射速度大于7.9km/s,会怎样?
如果人造地球卫星进入地面附近的轨道速度大于7.9km/s,它绕地球运动的轨迹是椭圆。
第二宇宙速度:
当卫星的速度等于或大于11.2km/s时,卫星就会脱离地球的引力,不再绕地球运行。这个速度叫第二宇宙速度。
第三宇宙速度:如果物体的速度等于或大于16.7km/s,物体就摆脱了太阳引力的束缚,飞到太阳系以外的宇宙空间去。这个速度叫第三宇宙速度。
V1=7.9km/s
地球
V2=11.2km/s
V3=16.7km/s
【问题探究3】卫星运行时,其向心加速度、线速度、角速度、周期,分别与其轨道半径的关系。
项目 推导式 关系式 结论
v与r的关系
ω与r的关系
T与r的关系
a与r的关系
【结论】高轨,低速,大周期,小加速度。
r越大 ω越小
r越大 T越大
r越大 a越小
r越大 v越小
1、 我国发射的一颗绕月运行的探月卫星“嫦娥1号”,设该卫星的轨道是圆形的,且贴近月球表面.已知月球的质量约为地球质量的 ,月球的半径约为地球半径的 ,地球上的第一宇宙速度约为7.9 km/s,则该探月卫星绕月运行的速率约为( )
A、0.4 km/s B、1.8 km/s
C、11 km/s D、36 km/s
√
√
地球同步卫星
所谓地球同步卫星,是相对于地面静止的和地球具有相同周期的卫星,同步卫星必须位于赤道平面内,且到地面的高度一定。
r v w T a
“全部固定”
T=1天=86400秒
h=36000Km
V=3.07Km/s
F引>F向
F引
距离地球5500万光年
质量约为太阳的65亿倍
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
