4.1光的折射定律 练习(word版含答案)
文档属性
| 名称 | 4.1光的折射定律 练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-13 04:59:12 | ||
图片预览


文档简介
粤教版(2019)选择性必修一 4.1 光的折射定律
一、单选题
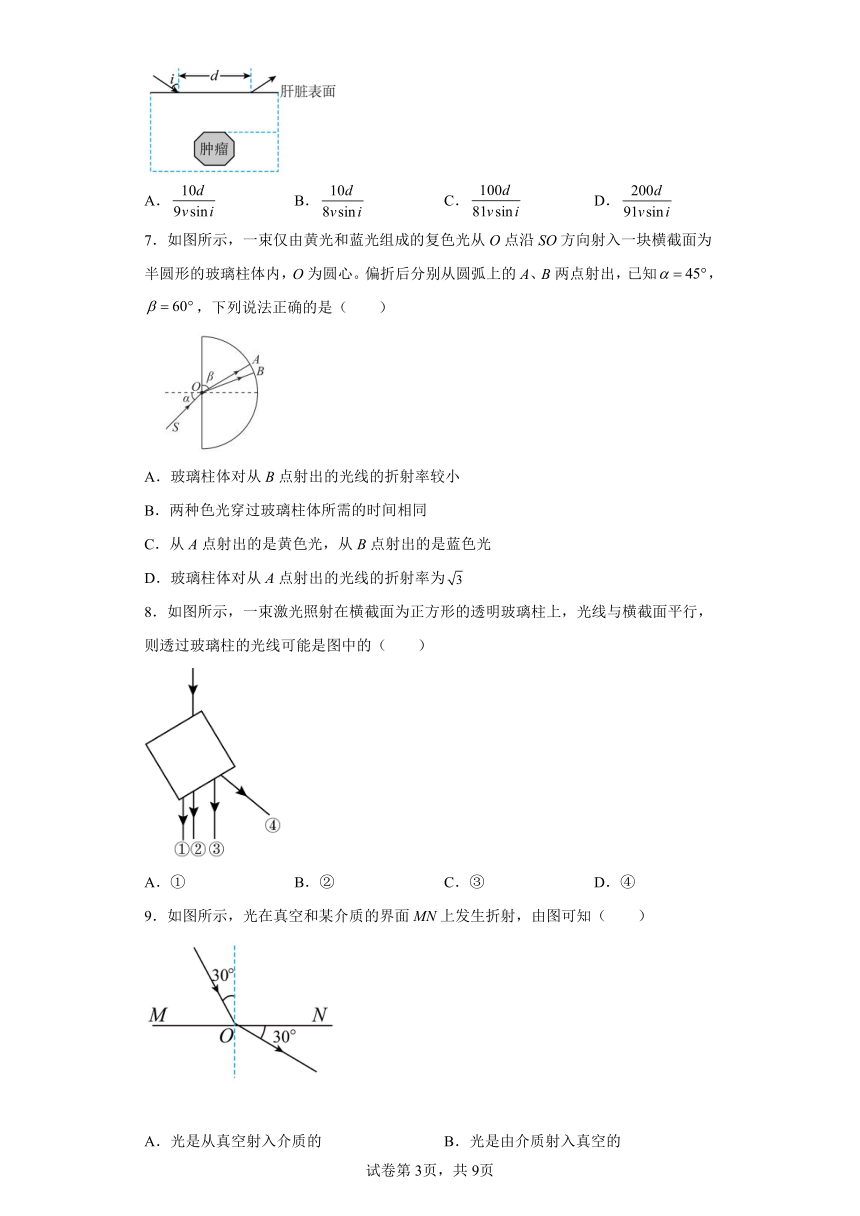
1.如图所示,一束光线通过一水平界面从某介质射入真空,已知入射光线与界面的夹角为60°,折射光线与界面的夹角为45°,则该介质的折射率为( )
A. B. C. D.
2.如图所示,注满水的透明玻璃水缸中有一位男子手持一张写有“PHYSICS IS PHUN”的纸片,将自己的头部露出水面。从照片中可以看到该男子在水中的身体与其头部有明显的错位,造成这种视觉现象的主要原因是( )
A.光的反射 B.光的折射
C.光的干涉 D.光的衍射
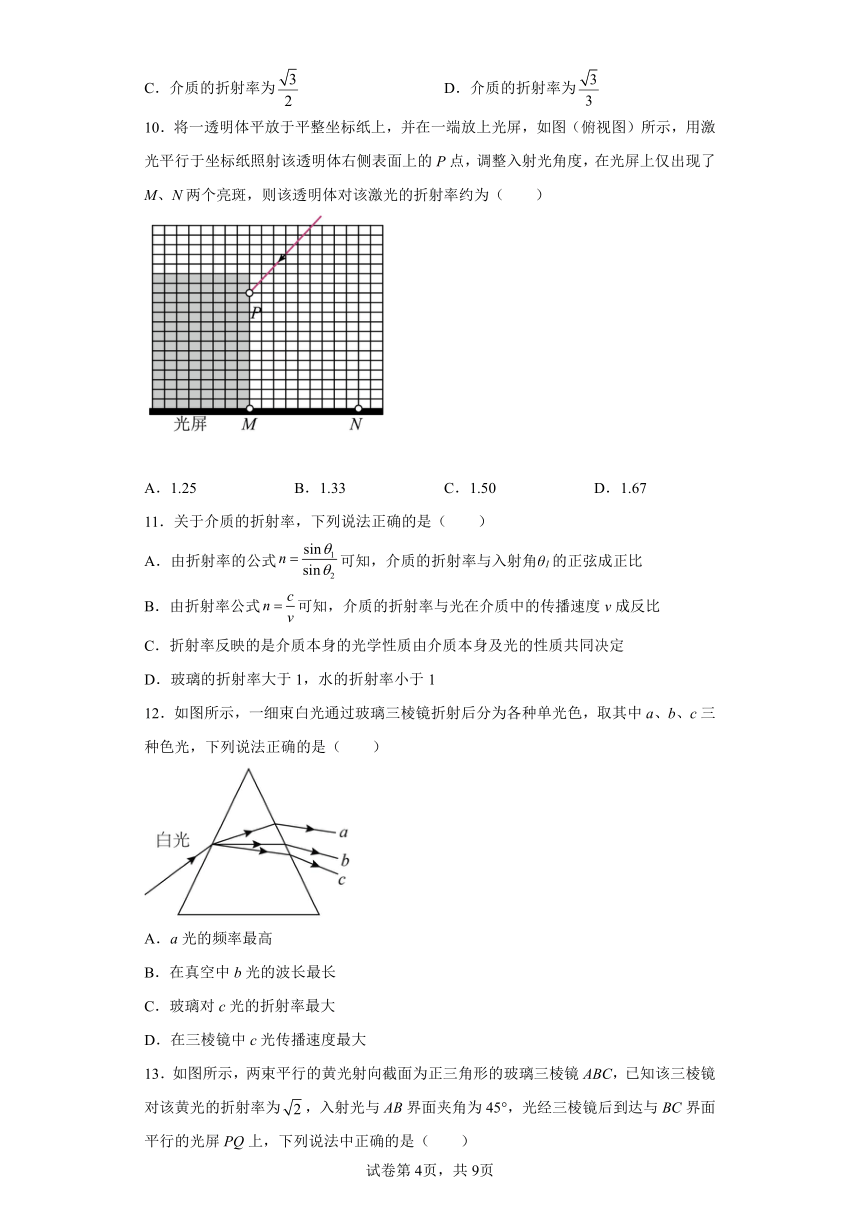
3.如图所示,一束黄光和一束蓝光,从O点以相同角度沿PO方向射入横截面为半圆形的玻璃柱体,其透射光线分别从M、N两点射出,已知α=45°,β=60°,光速c=3×108 m/s则下列说法正确的是( )
A.两束光穿过玻璃柱体所需时间相同
B.PM是蓝光,PN是黄光
C.玻璃对PM光束的折射率为
D.PM光束在该玻璃中传播的速度为×108 m/s
4.如图所示是光线以相同的入射角从空气射入三种不同介质时的折射情况,则在三种介质中光的传播速度最小的是( )
A.介质甲 B.介质乙 C.介质丙 D.三种介质均一样
5.如图所示,为某种玻璃制成的三棱镜的横截面,其中长度为。今有一束单色光从P点垂直边入射,边边上的M点出射,出射方向与的夹角为,则玻璃的折射率为( )
A. B. C. D.
6.“B超”可用于探测人体内脏的病变状况。超声波从某肿瘤患者的肝脏表面入射,经折射与反射,最后从肝脏表面射出,示意图如图所示。超声波在进入肝脏发生折射时遵循的规律与光的折射规律类似。可表示为(式中是入射角,是折射角,、分别是超声波在肝外和肝内的折射率),超声波在肿瘤表面发生反射时遵循的规律与光的反射规律相同。已知,超声波在肝内的传播速度为v,入射角为i,肿瘤的反射面恰好与肝脏表面平行,肝脏表面入射点到出射点之间的距离为d,则超声波在肝内的传播时间为( )
A. B. C. D.
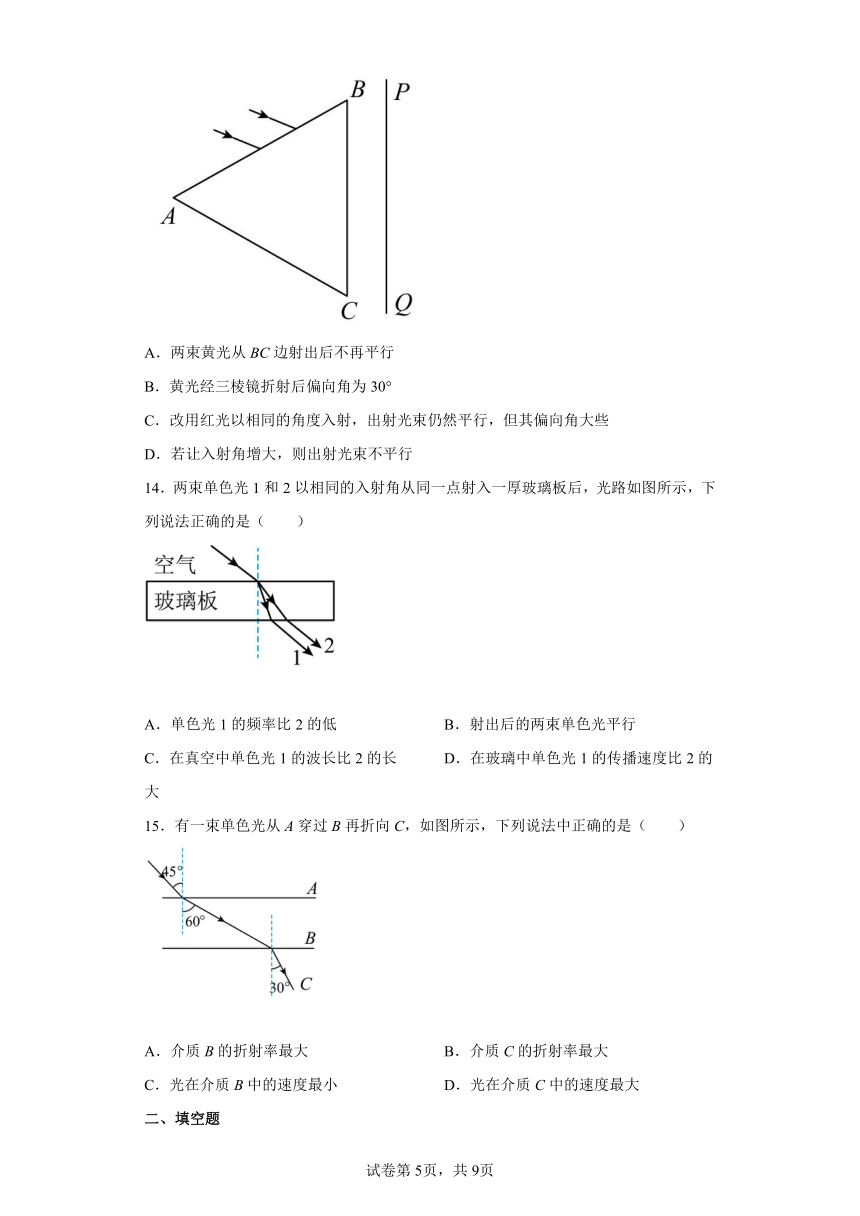
7.如图所示,一束仅由黄光和蓝光组成的复色光从O点沿SO方向射入一块横截面为半圆形的玻璃柱体内,O为圆心。偏折后分别从圆弧上的A、B两点射出,已知,,下列说法正确的是( )
A.玻璃柱体对从B点射出的光线的折射率较小
B.两种色光穿过玻璃柱体所需的时间相同
C.从A点射出的是黄色光,从B点射出的是蓝色光
D.玻璃柱体对从A点射出的光线的折射率为
8.如图所示,一束激光照射在横截面为正方形的透明玻璃柱上,光线与横截面平行,则透过玻璃柱的光线可能是图中的( )
A.① B.② C.③ D.④
9.如图所示,光在真空和某介质的界面MN上发生折射,由图可知( )
A.光是从真空射入介质的 B.光是由介质射入真空的
C.介质的折射率为 D.介质的折射率为
10.将一透明体平放于平整坐标纸上,并在一端放上光屏,如图(俯视图)所示,用激光平行于坐标纸照射该透明体右侧表面上的P点,调整入射光角度,在光屏上仅出现了M、N两个亮斑,则该透明体对该激光的折射率约为( )
A.1.25 B.1.33 C.1.50 D.1.67
11.关于介质的折射率,下列说法正确的是( )
A.由折射率的公式可知,介质的折射率与入射角θ1的正弦成正比
B.由折射率公式可知,介质的折射率与光在介质中的传播速度v成反比
C.折射率反映的是介质本身的光学性质由介质本身及光的性质共同决定
D.玻璃的折射率大于1,水的折射率小于1
12.如图所示,一细束白光通过玻璃三棱镜折射后分为各种单光色,取其中a、b、c三种色光,下列说法正确的是( )
A.a光的频率最高
B.在真空中b光的波长最长
C.玻璃对c光的折射率最大
D.在三棱镜中c光传播速度最大
13.如图所示,两束平行的黄光射向截面为正三角形的玻璃三棱镜ABC,已知该三棱镜对该黄光的折射率为,入射光与AB界面夹角为45°,光经三棱镜后到达与BC界面平行的光屏PQ上,下列说法中正确的是( )
A.两束黄光从BC边射出后不再平行
B.黄光经三棱镜折射后偏向角为30°
C.改用红光以相同的角度入射,出射光束仍然平行,但其偏向角大些
D.若让入射角增大,则出射光束不平行
14.两束单色光1和2以相同的入射角从同一点射入一厚玻璃板后,光路如图所示,下列说法正确的是( )
A.单色光1的频率比2的低 B.射出后的两束单色光平行
C.在真空中单色光1的波长比2的长 D.在玻璃中单色光1的传播速度比2的大
15.有一束单色光从A穿过B再折向C,如图所示,下列说法中正确的是( )
A.介质B的折射率最大 B.介质C的折射率最大
C.光在介质B中的速度最小 D.光在介质C中的速度最大
二、填空题
16.折射定律
(1)内容:如图所示,折射光线与入射光线、法线处在______内,折射光线与入射光线分别位于法线的______;入射角的正弦与折射角的正弦成______比;
(2)表达式:=n12(n12为比例常数)。
17.某同学测量玻璃破的折射率,准备了下列器材:激光笔、直尺、刻度尺、一面镀有反射膜的平行玻璃砖.如图所示,直尺与玻璃砖平行放置,激光笔发出的一束激光从直尺上O点射向玻璃砖表面,在直尺观察到A、B两个光点,读出OA间的距离为20.00cm,AB的间距为5.77cm,测得图中直尺到玻璃砖上表面距离d1=10.00cm,取玻璃砖厚度d2=5.00cm.玻璃的折射率n=______,光在玻璃中传播速度v=______m/s(光在真空中传播速度c=3.0×108m/s,tan30°=0.577).
18.如图所示为玻璃厚度检测仪的原理简图,其原理是:固定一束激光AO以不变的入射角θ1照到MN表面,折射后从PQ表面射出,折射光线最后照到光电管C上,光电管将光信号转变为电信号,依据激光束在C上移动的距离,可以确定玻璃厚度的变化.设θ1=45°,玻璃对该光的折射率为,C上的光斑向左移动了Δs,则可确定玻璃的厚度比原来变____________(填“厚”或“薄”)了的__________倍.
19.使太阳光垂直照射到一块遮光板,板上有可以自由收缩的正方形孔,孔的后面放置一个光屏,在正方形孔逐渐变小直至闭合的过程中,光屏上依次可以看到几种不同的现象,试把下列现象依次排列:________。
A.圆形光斑
B.明暗相间的彩色条纹
C.变暗消失
D.正方形光斑
E.正方形光斑由大变小
三、解答题
20.如图所示,在某液体内部有一边缘厚度不计、高度为d、内部为真空的透明长方体。现有一束由红光和紫光组成的宽度为的平行复色光,以的入射角射向长方体上表面。已知该种液体对红、紫光的折射率分别为和,,,则:
(1)红光和紫光在第一个分界面上的折射角;
(2)d至少多大时从下表面射出的红光和紫光能够分离?(保留三位有效数字)
21.如图,竖直放置在水平地面上的长方形玻璃砖折射率。一束单色光以入射角射到玻璃砖右表面的中点A,经左、右两表面传播后在地面上出现三个光点(图中未画出)。已知玻璃砖的高度,厚度,不考虑多次反射,以右表面O点为一维坐标原点,向右为正方向。求地面上三个光点的坐标位置。
22.如图所示,一个盛水容器内装有深度为H的水,激光笔发出一束激光射向水面O点,经折射后在水槽底部形成一光斑P。已知入射角,水的折射率,真空中光速为c,,。求:
(1)激光从O点传播到P点的时间t;
(2)打开出水口放水,当水面下降到原来一半深度时,光斑P仍然在容器底部,求光斑P移动的距离x。
23.如图所示,假设一条自身能发光的鱼在水面下一定深度处水平向岸边匀速游动,岸上地面水平,且地面上有一竖直高塔,鱼发出的光束始终与水平面成53°角,光束投到塔上的光斑高度在1s内下移了。已知鱼游动的速度,光束从鱼处发出至传播到水面的时间为3×10-8s。取,,真空中的光速,求:
①水对该光的折射率;
②该鱼在水中的深度为h。
24.如图所示的直角三角形ABC是柱形玻璃砖的横截面,∠A=30°,∠B=90°,BC的长为L,BC所在的玻璃砖面镀银,E为BC边的中点。一束平行于AB的光束从AC边上的某点射入玻璃砖,进入玻璃砖后(光线未在图中画出),在BC边上的E点被反射,EF是该反射光线,且EF恰与AC平行。求:
(1)作出光从空气进入玻璃砖到出玻璃砖的光路图。
(2)该玻璃砖的折射率;
(3)该光束从AC边上射入玻璃砖后在玻璃砖中传播的时间(光在真空中的速度为c)。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【详解】
如图所示,由几何知识可得
入射角
i=90°-60°=30°
折射角
r=90°-45°=45°
由于光线从介质射入真空,则有
解得
故选C。
2.B
【详解】
从照片中可以看到该男子在水中的身体与其头部有明显的错位,是由于光在水面处发生折射形成的,B正确,ACD错误。
故选B。
3.C
【详解】
A.由图可知,从M点射出的光的折射率较小,从N点射出的光的折射率较大,根据折射率与光速的关系可知,从M点射出的光的速度较大。两束光穿过玻璃柱体的路程相等,速度不同,所需时间不相同,选项A错误;
B.根据蓝光折射率大于黄光可知,PM是黄光,PN是蓝光,选项B错误;
C.由折射定律可知,玻璃对PM光束的折射率为
选项C正确;
D.PM光束在该玻璃中传播的速度为
选项D错误;
故选C。
4.C
【详解】
从题图中可以看出在入射角i相同的情况下,介质丙中折射角r最小,由
可知,介质丙对光的折射率最大,由
可知,在介质丙中光的传播速度最小。
故选C。
5.C
【详解】
光从BC射入,从AC射出,则在AB边发生全反射,由于不考虑光的多次反射,则光线在玻璃中的光路图如图所示
由几何关系可得
光在AC边M点
玻璃的折射率为
故选C。
6.A
【详解】
作出光路图如下,设光在肝脏表面折射角为r,则有
光在肝脏内的光程为
则超声波在肝内的传播时间为
故A正确,BCD错误;
故选A。
7.C
【详解】
A.由图及
可知从A点射出的光线折射率较小,从B点射出的光线的折射率较大,A错误;
B.根据折射率与光速的关系可知从A点射出的光线在玻璃柱体中的速度较大,两种色光穿过玻璃柱体的路程相等,速度不同,所需的时间不相同,B错误;
C.蓝色光线的折射率大于黄色光线的折射率,所以从A点射出的是黄色光,从B点射出的是蓝色光,C正确;
D.由折射定律可知玻璃柱体对从A点射出的光线的折射率为
D错误。
故选C。
8.C
【详解】
根据折射定律
解得 ,所以折射光线向右偏折;根据折射定律
解得 ,所以出射光线与入射光线平行。
故选C。
9.B
【详解】
AB.光从光密介质射向光疏介质时,折射角大于入射角,根据题图可知,入射角为30°,折射角为60°,光是从介质射入真空的,A错误,B正确;
CD.由折射定律可知,介质的折射率为
CD错误。
故选B。
10.B
【详解】
由题意可知,光点N是由设到P点的光线直接反射后射到N点;而光斑M是由射到P点的光折射后射到左侧表面,然后发生全反射射到M点;
则在P点,由光的折射定律结合几何关系可知
故选B。
11.B
【详解】
A.折射率的公式
运用比值法定义,可知介质的折射率与入射角θ1、折射角的正弦θ2无关, A错误;
B.由公式
知c不变,则介质的折射率与介质中的波速成反比,B正确;
C.折射率反映的是介质本身的光学性质,介质的折射率只由介质本身决定,C错误;
D.因折射率是光线从空气折射入介质时的入射角和折射角的正弦值之比,任何介质的折射率都大于1,D错误。
故选B。
12.C
【详解】
AB.由光路图可知,a光的偏折程度最小,则a光的折射率最小,a光的频率最低,据
知,a光在真空中波长最长,故AB错误;
CD.由光路图可知,c光的偏折程度最大,c光的折射率最大;根据
c光在棱镜中传播速度最小,故C项正确,D项错误。
故选C。
13.B
【详解】
AB.作出光路图如图,由折射率公式n= 可知
r=30°
由几何关系可知折射光在三棱镜内平行于底边AC,由对称性可知其在BC边射出时的出射角也为i=45°,因此光束的偏向角为30°,A错误,B正确;
C.由于同种材料对不同的色光的折射率不同,相对于黄光而言红光的折射率小,因此折射后红光的偏向角小些,C错误;
D.若让入射角增大,折射角按一定的比例增大,出射光束仍然平行,D错误。
故选B。
14.B
【详解】
A.由题图可知,两束单色光的入射角i相等,单色光1的折射角小于单色光2的折射角,根据折射定律
可知,玻璃对单色光1的折射率大于对单色光2的折射率,单色光1的频率大于单色光2的频率,A错误;
B.根据几何关系可知,折射光线射到平行玻璃板下表面的入射角等于上表面的折射角,根据光路可逆性可知,光线射出下表面时的折射角等于射入上表面的入射角,故两条出射光线平行,B正确;
C.由可知,真空中单色光1的波长小于单色光2的波长,C错误;
D.根据可知,在玻璃中单色光1的传播速度小于单色光2的传播速度,D错误。
故选B。
15.B
【详解】
AB.由光路的可逆性,假设光分别由B进入A和C,根据折射率的物理意义可知,折射率是反映介质对光线偏折程度的物理量,进入C的偏折程度大于进入A的偏折程度,可知C的折射率比A的大,B中的入射角最大,折射率最小,可得
nC>nA>nB
A错误,B正确;
CD.由可以判断出,光在B中传播的速度最大,在C中传播的速度最小,CD错误。
故选B。
16. 同一平面 两侧 正
【详解】
略
【点睛】
17. 2.12×108
【详解】
作出光路图如图所示.根据几何知识可知:i=45°,DE=AB=5.77cm
且有:,则得 r=30°
所以玻璃的折射率
光在玻璃中传播速度
18. 厚
光线通过玻璃砖后传播方向不变,只发生侧移,根据激光束在C上移动的方向,可以确定玻璃厚度的变化情况.由折射定律和几何知识求解玻璃厚度的变化量.
【详解】
[1]根据平行玻璃砖的光学特性可知,光线通过玻璃砖后传播方向不变,只发生侧移,据题激光束在C的光斑向左移动,说明玻璃砖增厚;
[2]根据折射定律得
得
得
设玻璃砖变厚了d.根据几何知识得
解得
19.DEABC
【详解】
由于光的波长很短,因此当孔很大时,不会发生明显的衍射现象,此时光可看做是近似直线传播,在屏上得到孔的影即正方形光斑,随着孔的收缩正方形光斑由大变小;当孔继续减小时,虽不能使光发生明显的衍射现象,但可以在屏上得到太阳的像,小孔成像即圆形光斑;孔再继续减小时,光开始发生明显的衍射现象,出现明暗相间的彩色条纹;孔进一步减小直到闭合时,由于穿过光的能量减小而使光线变暗直至消失,故顺序为DEABC。
20.(1)53°;60°;(2)12.5cm
【详解】
(1)设红光的折射角为,紫光的折射角为,则
解得
,
(2)如图所示,由几何关系得
解得
21.;;
【详解】
画出相应光路,如图所示
由折射定律可得
解得折射角为
由几何关系可知,从B点折射出的光线与从A点直接反射的光线平行,有
解得
,
则
标尺上三光点的坐标为
M:4cm,,
22.(1);(2)
【详解】
(1)根据折射定理
解得折射角大小
β=37°
光在水中的速度
激光从O点传播到P点的时间
(2)根据
由几何关系有:
x=h(tanα-tanβ)
当,代入数据解得
【点睛】
23.(1);(2)
【详解】
(1)光的传播的几何关系所示
可知光线由水中入射到空气的过程中,入射角为
折射角为
因此,水对该光的折射率
(2)光束从鱼处发出至传播到水面的距离为
该鱼在水中的深度为
24.(1);(2);(3)
【详解】
(1)作出光路图如图
(2)由几何关系可知,光线在AC面上的入射角为60°,折射角为30°
则折射率为
(3)因为发生全反射的临界角的正弦值为
sinC=
因为,所以临界角C满足
30°光线在F点发生全反射,然后从H点射出玻璃砖,则在玻璃砖中传播的距离为
其中
联立解得
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图所示,一束光线通过一水平界面从某介质射入真空,已知入射光线与界面的夹角为60°,折射光线与界面的夹角为45°,则该介质的折射率为( )
A. B. C. D.
2.如图所示,注满水的透明玻璃水缸中有一位男子手持一张写有“PHYSICS IS PHUN”的纸片,将自己的头部露出水面。从照片中可以看到该男子在水中的身体与其头部有明显的错位,造成这种视觉现象的主要原因是( )
A.光的反射 B.光的折射
C.光的干涉 D.光的衍射
3.如图所示,一束黄光和一束蓝光,从O点以相同角度沿PO方向射入横截面为半圆形的玻璃柱体,其透射光线分别从M、N两点射出,已知α=45°,β=60°,光速c=3×108 m/s则下列说法正确的是( )
A.两束光穿过玻璃柱体所需时间相同
B.PM是蓝光,PN是黄光
C.玻璃对PM光束的折射率为
D.PM光束在该玻璃中传播的速度为×108 m/s
4.如图所示是光线以相同的入射角从空气射入三种不同介质时的折射情况,则在三种介质中光的传播速度最小的是( )
A.介质甲 B.介质乙 C.介质丙 D.三种介质均一样
5.如图所示,为某种玻璃制成的三棱镜的横截面,其中长度为。今有一束单色光从P点垂直边入射,边边上的M点出射,出射方向与的夹角为,则玻璃的折射率为( )
A. B. C. D.
6.“B超”可用于探测人体内脏的病变状况。超声波从某肿瘤患者的肝脏表面入射,经折射与反射,最后从肝脏表面射出,示意图如图所示。超声波在进入肝脏发生折射时遵循的规律与光的折射规律类似。可表示为(式中是入射角,是折射角,、分别是超声波在肝外和肝内的折射率),超声波在肿瘤表面发生反射时遵循的规律与光的反射规律相同。已知,超声波在肝内的传播速度为v,入射角为i,肿瘤的反射面恰好与肝脏表面平行,肝脏表面入射点到出射点之间的距离为d,则超声波在肝内的传播时间为( )
A. B. C. D.
7.如图所示,一束仅由黄光和蓝光组成的复色光从O点沿SO方向射入一块横截面为半圆形的玻璃柱体内,O为圆心。偏折后分别从圆弧上的A、B两点射出,已知,,下列说法正确的是( )
A.玻璃柱体对从B点射出的光线的折射率较小
B.两种色光穿过玻璃柱体所需的时间相同
C.从A点射出的是黄色光,从B点射出的是蓝色光
D.玻璃柱体对从A点射出的光线的折射率为
8.如图所示,一束激光照射在横截面为正方形的透明玻璃柱上,光线与横截面平行,则透过玻璃柱的光线可能是图中的( )
A.① B.② C.③ D.④
9.如图所示,光在真空和某介质的界面MN上发生折射,由图可知( )
A.光是从真空射入介质的 B.光是由介质射入真空的
C.介质的折射率为 D.介质的折射率为
10.将一透明体平放于平整坐标纸上,并在一端放上光屏,如图(俯视图)所示,用激光平行于坐标纸照射该透明体右侧表面上的P点,调整入射光角度,在光屏上仅出现了M、N两个亮斑,则该透明体对该激光的折射率约为( )
A.1.25 B.1.33 C.1.50 D.1.67
11.关于介质的折射率,下列说法正确的是( )
A.由折射率的公式可知,介质的折射率与入射角θ1的正弦成正比
B.由折射率公式可知,介质的折射率与光在介质中的传播速度v成反比
C.折射率反映的是介质本身的光学性质由介质本身及光的性质共同决定
D.玻璃的折射率大于1,水的折射率小于1
12.如图所示,一细束白光通过玻璃三棱镜折射后分为各种单光色,取其中a、b、c三种色光,下列说法正确的是( )
A.a光的频率最高
B.在真空中b光的波长最长
C.玻璃对c光的折射率最大
D.在三棱镜中c光传播速度最大
13.如图所示,两束平行的黄光射向截面为正三角形的玻璃三棱镜ABC,已知该三棱镜对该黄光的折射率为,入射光与AB界面夹角为45°,光经三棱镜后到达与BC界面平行的光屏PQ上,下列说法中正确的是( )
A.两束黄光从BC边射出后不再平行
B.黄光经三棱镜折射后偏向角为30°
C.改用红光以相同的角度入射,出射光束仍然平行,但其偏向角大些
D.若让入射角增大,则出射光束不平行
14.两束单色光1和2以相同的入射角从同一点射入一厚玻璃板后,光路如图所示,下列说法正确的是( )
A.单色光1的频率比2的低 B.射出后的两束单色光平行
C.在真空中单色光1的波长比2的长 D.在玻璃中单色光1的传播速度比2的大
15.有一束单色光从A穿过B再折向C,如图所示,下列说法中正确的是( )
A.介质B的折射率最大 B.介质C的折射率最大
C.光在介质B中的速度最小 D.光在介质C中的速度最大
二、填空题
16.折射定律
(1)内容:如图所示,折射光线与入射光线、法线处在______内,折射光线与入射光线分别位于法线的______;入射角的正弦与折射角的正弦成______比;
(2)表达式:=n12(n12为比例常数)。
17.某同学测量玻璃破的折射率,准备了下列器材:激光笔、直尺、刻度尺、一面镀有反射膜的平行玻璃砖.如图所示,直尺与玻璃砖平行放置,激光笔发出的一束激光从直尺上O点射向玻璃砖表面,在直尺观察到A、B两个光点,读出OA间的距离为20.00cm,AB的间距为5.77cm,测得图中直尺到玻璃砖上表面距离d1=10.00cm,取玻璃砖厚度d2=5.00cm.玻璃的折射率n=______,光在玻璃中传播速度v=______m/s(光在真空中传播速度c=3.0×108m/s,tan30°=0.577).
18.如图所示为玻璃厚度检测仪的原理简图,其原理是:固定一束激光AO以不变的入射角θ1照到MN表面,折射后从PQ表面射出,折射光线最后照到光电管C上,光电管将光信号转变为电信号,依据激光束在C上移动的距离,可以确定玻璃厚度的变化.设θ1=45°,玻璃对该光的折射率为,C上的光斑向左移动了Δs,则可确定玻璃的厚度比原来变____________(填“厚”或“薄”)了的__________倍.
19.使太阳光垂直照射到一块遮光板,板上有可以自由收缩的正方形孔,孔的后面放置一个光屏,在正方形孔逐渐变小直至闭合的过程中,光屏上依次可以看到几种不同的现象,试把下列现象依次排列:________。
A.圆形光斑
B.明暗相间的彩色条纹
C.变暗消失
D.正方形光斑
E.正方形光斑由大变小
三、解答题
20.如图所示,在某液体内部有一边缘厚度不计、高度为d、内部为真空的透明长方体。现有一束由红光和紫光组成的宽度为的平行复色光,以的入射角射向长方体上表面。已知该种液体对红、紫光的折射率分别为和,,,则:
(1)红光和紫光在第一个分界面上的折射角;
(2)d至少多大时从下表面射出的红光和紫光能够分离?(保留三位有效数字)
21.如图,竖直放置在水平地面上的长方形玻璃砖折射率。一束单色光以入射角射到玻璃砖右表面的中点A,经左、右两表面传播后在地面上出现三个光点(图中未画出)。已知玻璃砖的高度,厚度,不考虑多次反射,以右表面O点为一维坐标原点,向右为正方向。求地面上三个光点的坐标位置。
22.如图所示,一个盛水容器内装有深度为H的水,激光笔发出一束激光射向水面O点,经折射后在水槽底部形成一光斑P。已知入射角,水的折射率,真空中光速为c,,。求:
(1)激光从O点传播到P点的时间t;
(2)打开出水口放水,当水面下降到原来一半深度时,光斑P仍然在容器底部,求光斑P移动的距离x。
23.如图所示,假设一条自身能发光的鱼在水面下一定深度处水平向岸边匀速游动,岸上地面水平,且地面上有一竖直高塔,鱼发出的光束始终与水平面成53°角,光束投到塔上的光斑高度在1s内下移了。已知鱼游动的速度,光束从鱼处发出至传播到水面的时间为3×10-8s。取,,真空中的光速,求:
①水对该光的折射率;
②该鱼在水中的深度为h。
24.如图所示的直角三角形ABC是柱形玻璃砖的横截面,∠A=30°,∠B=90°,BC的长为L,BC所在的玻璃砖面镀银,E为BC边的中点。一束平行于AB的光束从AC边上的某点射入玻璃砖,进入玻璃砖后(光线未在图中画出),在BC边上的E点被反射,EF是该反射光线,且EF恰与AC平行。求:
(1)作出光从空气进入玻璃砖到出玻璃砖的光路图。
(2)该玻璃砖的折射率;
(3)该光束从AC边上射入玻璃砖后在玻璃砖中传播的时间(光在真空中的速度为c)。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【详解】
如图所示,由几何知识可得
入射角
i=90°-60°=30°
折射角
r=90°-45°=45°
由于光线从介质射入真空,则有
解得
故选C。
2.B
【详解】
从照片中可以看到该男子在水中的身体与其头部有明显的错位,是由于光在水面处发生折射形成的,B正确,ACD错误。
故选B。
3.C
【详解】
A.由图可知,从M点射出的光的折射率较小,从N点射出的光的折射率较大,根据折射率与光速的关系可知,从M点射出的光的速度较大。两束光穿过玻璃柱体的路程相等,速度不同,所需时间不相同,选项A错误;
B.根据蓝光折射率大于黄光可知,PM是黄光,PN是蓝光,选项B错误;
C.由折射定律可知,玻璃对PM光束的折射率为
选项C正确;
D.PM光束在该玻璃中传播的速度为
选项D错误;
故选C。
4.C
【详解】
从题图中可以看出在入射角i相同的情况下,介质丙中折射角r最小,由
可知,介质丙对光的折射率最大,由
可知,在介质丙中光的传播速度最小。
故选C。
5.C
【详解】
光从BC射入,从AC射出,则在AB边发生全反射,由于不考虑光的多次反射,则光线在玻璃中的光路图如图所示
由几何关系可得
光在AC边M点
玻璃的折射率为
故选C。
6.A
【详解】
作出光路图如下,设光在肝脏表面折射角为r,则有
光在肝脏内的光程为
则超声波在肝内的传播时间为
故A正确,BCD错误;
故选A。
7.C
【详解】
A.由图及
可知从A点射出的光线折射率较小,从B点射出的光线的折射率较大,A错误;
B.根据折射率与光速的关系可知从A点射出的光线在玻璃柱体中的速度较大,两种色光穿过玻璃柱体的路程相等,速度不同,所需的时间不相同,B错误;
C.蓝色光线的折射率大于黄色光线的折射率,所以从A点射出的是黄色光,从B点射出的是蓝色光,C正确;
D.由折射定律可知玻璃柱体对从A点射出的光线的折射率为
D错误。
故选C。
8.C
【详解】
根据折射定律
解得 ,所以折射光线向右偏折;根据折射定律
解得 ,所以出射光线与入射光线平行。
故选C。
9.B
【详解】
AB.光从光密介质射向光疏介质时,折射角大于入射角,根据题图可知,入射角为30°,折射角为60°,光是从介质射入真空的,A错误,B正确;
CD.由折射定律可知,介质的折射率为
CD错误。
故选B。
10.B
【详解】
由题意可知,光点N是由设到P点的光线直接反射后射到N点;而光斑M是由射到P点的光折射后射到左侧表面,然后发生全反射射到M点;
则在P点,由光的折射定律结合几何关系可知
故选B。
11.B
【详解】
A.折射率的公式
运用比值法定义,可知介质的折射率与入射角θ1、折射角的正弦θ2无关, A错误;
B.由公式
知c不变,则介质的折射率与介质中的波速成反比,B正确;
C.折射率反映的是介质本身的光学性质,介质的折射率只由介质本身决定,C错误;
D.因折射率是光线从空气折射入介质时的入射角和折射角的正弦值之比,任何介质的折射率都大于1,D错误。
故选B。
12.C
【详解】
AB.由光路图可知,a光的偏折程度最小,则a光的折射率最小,a光的频率最低,据
知,a光在真空中波长最长,故AB错误;
CD.由光路图可知,c光的偏折程度最大,c光的折射率最大;根据
c光在棱镜中传播速度最小,故C项正确,D项错误。
故选C。
13.B
【详解】
AB.作出光路图如图,由折射率公式n= 可知
r=30°
由几何关系可知折射光在三棱镜内平行于底边AC,由对称性可知其在BC边射出时的出射角也为i=45°,因此光束的偏向角为30°,A错误,B正确;
C.由于同种材料对不同的色光的折射率不同,相对于黄光而言红光的折射率小,因此折射后红光的偏向角小些,C错误;
D.若让入射角增大,折射角按一定的比例增大,出射光束仍然平行,D错误。
故选B。
14.B
【详解】
A.由题图可知,两束单色光的入射角i相等,单色光1的折射角小于单色光2的折射角,根据折射定律
可知,玻璃对单色光1的折射率大于对单色光2的折射率,单色光1的频率大于单色光2的频率,A错误;
B.根据几何关系可知,折射光线射到平行玻璃板下表面的入射角等于上表面的折射角,根据光路可逆性可知,光线射出下表面时的折射角等于射入上表面的入射角,故两条出射光线平行,B正确;
C.由可知,真空中单色光1的波长小于单色光2的波长,C错误;
D.根据可知,在玻璃中单色光1的传播速度小于单色光2的传播速度,D错误。
故选B。
15.B
【详解】
AB.由光路的可逆性,假设光分别由B进入A和C,根据折射率的物理意义可知,折射率是反映介质对光线偏折程度的物理量,进入C的偏折程度大于进入A的偏折程度,可知C的折射率比A的大,B中的入射角最大,折射率最小,可得
nC>nA>nB
A错误,B正确;
CD.由可以判断出,光在B中传播的速度最大,在C中传播的速度最小,CD错误。
故选B。
16. 同一平面 两侧 正
【详解】
略
【点睛】
17. 2.12×108
【详解】
作出光路图如图所示.根据几何知识可知:i=45°,DE=AB=5.77cm
且有:,则得 r=30°
所以玻璃的折射率
光在玻璃中传播速度
18. 厚
光线通过玻璃砖后传播方向不变,只发生侧移,根据激光束在C上移动的方向,可以确定玻璃厚度的变化情况.由折射定律和几何知识求解玻璃厚度的变化量.
【详解】
[1]根据平行玻璃砖的光学特性可知,光线通过玻璃砖后传播方向不变,只发生侧移,据题激光束在C的光斑向左移动,说明玻璃砖增厚;
[2]根据折射定律得
得
得
设玻璃砖变厚了d.根据几何知识得
解得
19.DEABC
【详解】
由于光的波长很短,因此当孔很大时,不会发生明显的衍射现象,此时光可看做是近似直线传播,在屏上得到孔的影即正方形光斑,随着孔的收缩正方形光斑由大变小;当孔继续减小时,虽不能使光发生明显的衍射现象,但可以在屏上得到太阳的像,小孔成像即圆形光斑;孔再继续减小时,光开始发生明显的衍射现象,出现明暗相间的彩色条纹;孔进一步减小直到闭合时,由于穿过光的能量减小而使光线变暗直至消失,故顺序为DEABC。
20.(1)53°;60°;(2)12.5cm
【详解】
(1)设红光的折射角为,紫光的折射角为,则
解得
,
(2)如图所示,由几何关系得
解得
21.;;
【详解】
画出相应光路,如图所示
由折射定律可得
解得折射角为
由几何关系可知,从B点折射出的光线与从A点直接反射的光线平行,有
解得
,
则
标尺上三光点的坐标为
M:4cm,,
22.(1);(2)
【详解】
(1)根据折射定理
解得折射角大小
β=37°
光在水中的速度
激光从O点传播到P点的时间
(2)根据
由几何关系有:
x=h(tanα-tanβ)
当,代入数据解得
【点睛】
23.(1);(2)
【详解】
(1)光的传播的几何关系所示
可知光线由水中入射到空气的过程中,入射角为
折射角为
因此,水对该光的折射率
(2)光束从鱼处发出至传播到水面的距离为
该鱼在水中的深度为
24.(1);(2);(3)
【详解】
(1)作出光路图如图
(2)由几何关系可知,光线在AC面上的入射角为60°,折射角为30°
则折射率为
(3)因为发生全反射的临界角的正弦值为
sinC=
因为,所以临界角C满足
30°
其中
联立解得
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 动量和动量守恒定律
- 第一节 冲量 动量
- 第二节 动量定理
- 第三节 动量守恒定律
- 第四节 动量守恒定律的应用
- 第五节 弹性碰撞与非弹性碰撞
- 第六节 自然界中的守恒定律
- 第二章 机械振动
- 第一节 简谐运动
- 第二节 简谐运动的描述
- 第三节 单摆
- 第四节 用单摆测量重力加速度
- 第五节 受迫振动 共振
- 第三章 机械波
- 第一节 机械波的产生和传播
- 第二节 机械波的描述
- 第三节 机械波的传播现象
- 第四节 多普勒效应
- 本章复习与测试
- 第四章 光及其应用
- 第一节 光的折射定律
- 第二节 测定介质的折射率
- 第三节 光的全反射与光纤技术
- 第四节 光的干涉
- 第五节 用双缝干涉实验测定光的波长
- 第六节 光的衍射和偏振
- 第七节 激光
