2022年新教材高中数学第四章指数函数对数函数与幂函数章末检测(word版含解析)新人教B版必修第二册
文档属性
| 名称 | 2022年新教材高中数学第四章指数函数对数函数与幂函数章末检测(word版含解析)新人教B版必修第二册 |  | |
| 格式 | zip | ||
| 文件大小 | 117.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-13 07:59:37 | ||
图片预览



文档简介
指数函数、对数函数与幂函数
考试时间:120分钟 满分:150分
一、单项选择题(本题共8个小题,每小题5分,共40分,在每小题给出的四个选项中只有一个是符合题目要求的)
1.等于( )
A.lg9-1 B.1-lg9
C.8D.2
2.函数y=的定义域是( )
A.(-∞,2) B.(2,+∞)
C.(2,3)∪(3,+∞) D.(2,4)∪(4,+∞)
3.函数f(x)=的值域是( )
A.(-∞,1) B.(0,1)
C.(1,+∞) D.(-∞,1)∪(1,+∞)
4.若函数y=f(x)是函数y=ax(a>0且a≠1)的反函数,且f(2)=1,则f(x)=( )
A.log2xB.
C.logxD.2x-2
5.幂函数y=f(x)的图像过点(4,2),则幂函数y=f(x)的图像是( )
6.已知log32=a,3b=5,则log3用a,b表示为( )
A.(a+b+1) B.(a+b)+1
C.(a+b+1) D.a+b+1
7.已知,则( )
A.a>b>cB.b>a>c
C.a>c>bD.c>a>b
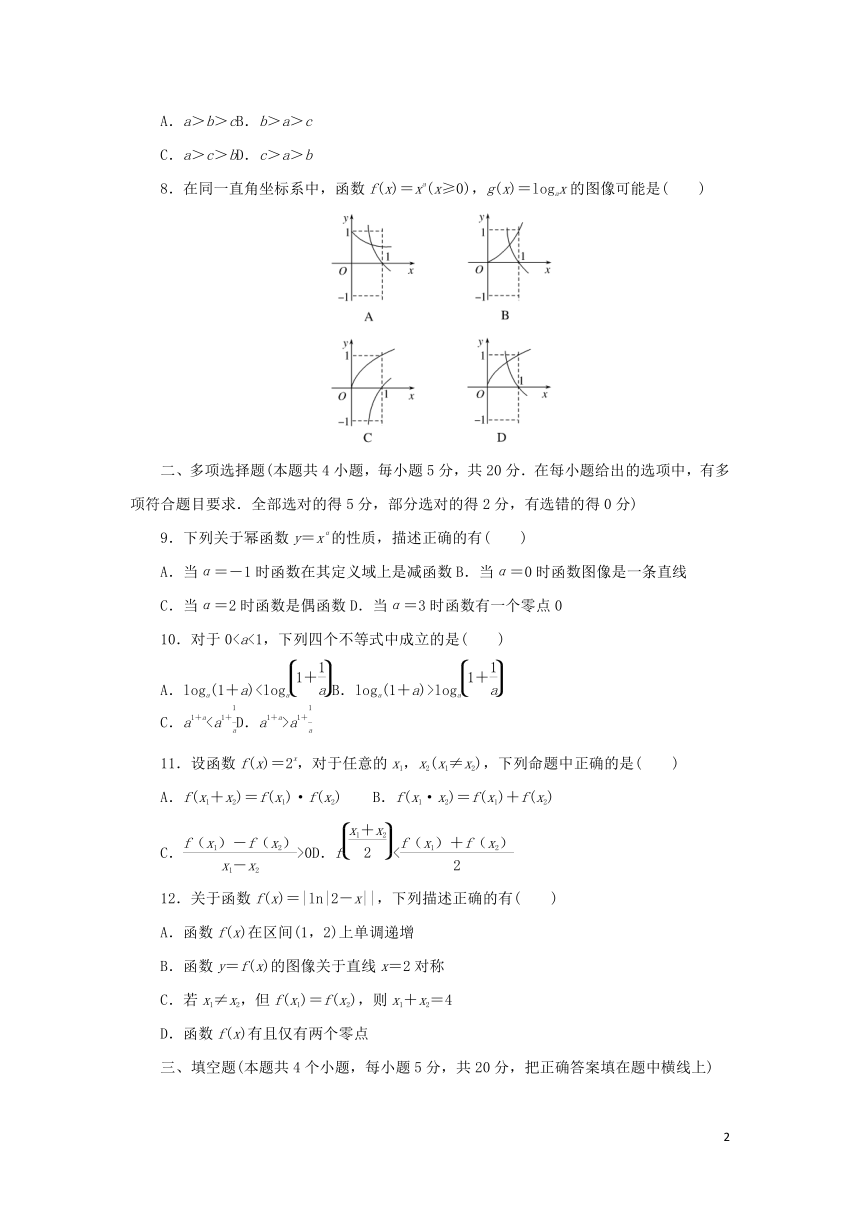
8.在同一直角坐标系中,函数f(x)=xa(x≥0),g(x)=logax的图像可能是( )
二、多项选择题(本题共4小题,毎小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.下列关于幂函数y=xα的性质,描述正确的有( )
A.当α=-1时函数在其定义域上是减函数B.当α=0时函数图像是一条直线
C.当α=2时函数是偶函数D.当α=3时函数有一个零点0
10.对于0A.loga(1+a)loga
C.a1+aa1+
11.设函数f(x)=2x,对于任意的x1,x2(x1≠x2),下列命题中正确的是( )
A.f(x1+x2)=f(x1)·f(x2) B.f(x1·x2)=f(x1)+f(x2)
C.>0D.f<
12.关于函数f(x)=|ln|2-x||,下列描述正确的有( )
A.函数f(x)在区间(1,2)上单调递增
B.函数y=f(x)的图像关于直线x=2对称
C.若x1≠x2,但f(x1)=f(x2),则x1+x2=4
D.函数f(x)有且仅有两个零点
三、填空题(本题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.设f(x)=则f(f(2))=________.
14.计算:+log2=________.
15.不等式x>的解集为________.
16.的值是________.
四、解答题(本题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(10分)计算:(1);
(2)÷100-+7log714.
18.(12分)已知函数f(x)=.
(1)求f(x)的单调区间;
(2)若f(x)的最大值等于,求a的值.
19.(12分)已知f(x)=log2(1+x)+log2(1-x).
(1)求函数f(x)的定义域.
(2)判断函数f(x)的奇偶性,并加以说明.
(3)求f的值.
20.(12分)函数f(x)=ax(a>0,且a≠1)在[1,2]上的最大值比最小值大,求a的值.
21.(12分)已知函数f(x)=a3-ax(a>0且a≠1).
(1)当a=2时,f(x)<4,求x的取值范围.
(2)若f(x)在[0,1]上的最小值大于1,求a的取值范围.
22.(12分)某工厂因排污比较严重,决定着手整治,一个月时污染度为60,整治后前四月的污染度如下表:
月数 1 2 3 4 …
污染度 60 31 13 0 …
污染度为0后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:
f(x)=20|x-4|(x≥1),g(x)=(x-4)2(x≥1),h(x)=30|log2x-2|(x≥1),其中x表示月数,f(x),g(x),h(x)分别表示污染度.
(1)选用哪个函数模拟比较合理,并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过60
章末质量检测(四) 指数函数、对数函数与幂函数
1.解析:因为lg9<lg10=1,所以=1-lg9.
答案:B
2.解析:由得x>2且x≠3,故选C.
答案:C
3.解析:∵3x+1>1,∴0<<1,∴函数值域为(0,1).
答案:B
4.解析:f(x)=logax,∵f(2)=1,∴loga2=1.∴a=2.
∴f(x)=log2x.
答案:A
5.解析:设幂函数的解析式为y=xα,∵幂函数y=f(x)的图像过点(4,2),∴2=4α,解得α=.∴y=,其定义域为[0,+∞),且是增函数.当0答案:C
6.解析:因为3b=5,所以b=log35,log3=log330=(log33+log32+log35)
=(1+a+b).
答案:A
7.解析:c=只需比较log23.4,log43.6,log3的大小,又0<log43.6<1,log23.4>log33.4>log3>1,所以a>c>b.
答案:C
8.解析:方法一 当a>1时,y=xa与y=logax均为增函数,但y=xa递增较快,排除C;当0<a<1时,y=xa为增函数,y=logax为减函数,排除A.由于y=xa递增较慢,所以选D.
方法二 幂函数f(x)=xa的图像不过(0,1)点,故A错;B项中由对数函数f(x)=logax的图像知0<a<1,而此时幂函数f(x)=xa的图像应是增长越来越慢的变化趋势,故B错,D对;C项中由对数函数f(x)=logax的图像知a>1,而此时幂函数f(x)=xa的图像应是增长越来越快的变化趋势,故C错.
答案:D
9.解析:对于A,α=-1时幂函数y=x-1在(-∞,0)和(0,+∞)是减函数,在其定义域上不是减函数,A错误;对于B,α=0时幂函数y=x0=1(x≠0),其图像是一条直线,去掉点(0,1),B错误;对于C,α=2时幂函数y=x2在定义域R上是偶函数,C正确;对于D,α=3时幂函数y=x3在R上的奇函数,且是增函数,有唯一零点是0,D正确.
答案:CD
10.解析:因为0所以loga(1+a)>loga.
又因为0a1+.故选B、D
答案:BD
11.解析:=,所以A成立,×≠,所以B不成立,函数f(x)=2x,在R上是单调递增函数,若x1>x2则f(x1)>f(x2),则>0,若x10,故C正确;f<说明函数是凹函数,而函数f(x)=2x是凹函数,故D正确.故选A、C、D.
答案:ACD
12.解析:函数f(x)=|ln|2-x||的图像如图所示:
由图可得:函数f(x)在区间(1,2)上单调递增,A正确;函数y=f(x)的图像关于直线x=2对称,B正确;若x1≠x2,但f(x1)=f(x2),则当x1,x2>2时,x1+x2>4,C错误;函数f(x)有且仅有两个零点,D正确.
答案:ABD
13.解析:因为f(2)=log3(22-1)=1,
所以f(f(2))=f(1)=2e1-1=2.
答案:2
14.解析:原式=|log25-2|+log25-1=log25-2-log25=-2.
答案:-2
15.解析:不等式>可化为-2x>,等价于x2-2x答案:{x|-116.解析:=====.
答案:
17.解析:(1)原式=-1-++[()-4]-=-1-++()3=+2=.
(2)原式=-(lg4+lg25)÷100-+14=-2÷10-1+14=-20+14=-6.
18.解析:(1)令t=|x|-a,则f(x)=,
不论a取何值,t在(-∞,0]上单调递减,在[0,+∞)上单调递增,
又y=是单调递减的,
因此f(x)的单调递增区间是(-∞,0],
单调递减区间是[0,+∞).
(2)由于f(x)的最大值是,且=,
所以g(x)=|x|-a应该有最小值-2,
从而a=2.
19.解析:(1)由得
即-1所以函数f(x)的定义域为{x|-1(2)函数f(x)为偶函数.证明如下:
因为函数f(x)的定义域为{x|-1又因为f(-x)=log2[1+(-x)]+log2[1-(-x)]=log2(1-x)+log2(1+x)=f(x),
所以函数f(x)=log2(1+x)+log2(1-x)为偶函数.
(3)f=log2+log2
=log2
=log2=log2=-1.
20.解析:分情况讨论:
①当0<a<1时,函数f(x)=ax(a>0,且a≠1)在[1,2]上的最大值f(x)max=f(1)=a1=a,最小值f(x)min=f(2)=a2,
∴a-a2=,解得a=或a=0(舍去);
②当a>1时,函数f(x)=ax(a>0,且a≠1)在[1,2]上的最大值f(x)max=f(2)=a2,最小值f(x)min=f(1)=a1=a,
∴a2-a=,解得a=或a=0(舍去).
综上所述,a=或a=.
21.解析:(1)当a=2时,f(x)=23-2x<4=22,3-2x<2,得x>.
(2)y=3-ax在定义域内单调递减,
当a>1时,函数f(x)在[0,1]上单调递减,f(x)min=f(1)=a3-a>1=a0,得1当01,不成立.
综上:122.解析:(1)用h(x)模拟比较合理,理由如下:
因为f(2)=40,g(2)≈26.7,
h(2)=30,f(3)=20,g(3)≈6.7,h(3)≈12.5,
由此可得h(x)更接近实际值,
所以用h(x)模拟比较合理.
(2)因为h(x)=30|log2x-2|在x≥4时是增函数,
又因为h(16)=60,故整治后有16个月的污染度不超过60.
9
考试时间:120分钟 满分:150分
一、单项选择题(本题共8个小题,每小题5分,共40分,在每小题给出的四个选项中只有一个是符合题目要求的)
1.等于( )
A.lg9-1 B.1-lg9
C.8D.2
2.函数y=的定义域是( )
A.(-∞,2) B.(2,+∞)
C.(2,3)∪(3,+∞) D.(2,4)∪(4,+∞)
3.函数f(x)=的值域是( )
A.(-∞,1) B.(0,1)
C.(1,+∞) D.(-∞,1)∪(1,+∞)
4.若函数y=f(x)是函数y=ax(a>0且a≠1)的反函数,且f(2)=1,则f(x)=( )
A.log2xB.
C.logxD.2x-2
5.幂函数y=f(x)的图像过点(4,2),则幂函数y=f(x)的图像是( )
6.已知log32=a,3b=5,则log3用a,b表示为( )
A.(a+b+1) B.(a+b)+1
C.(a+b+1) D.a+b+1
7.已知,则( )
A.a>b>cB.b>a>c
C.a>c>bD.c>a>b
8.在同一直角坐标系中,函数f(x)=xa(x≥0),g(x)=logax的图像可能是( )
二、多项选择题(本题共4小题,毎小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)
9.下列关于幂函数y=xα的性质,描述正确的有( )
A.当α=-1时函数在其定义域上是减函数B.当α=0时函数图像是一条直线
C.当α=2时函数是偶函数D.当α=3时函数有一个零点0
10.对于0
C.a1+a
11.设函数f(x)=2x,对于任意的x1,x2(x1≠x2),下列命题中正确的是( )
A.f(x1+x2)=f(x1)·f(x2) B.f(x1·x2)=f(x1)+f(x2)
C.>0D.f<
12.关于函数f(x)=|ln|2-x||,下列描述正确的有( )
A.函数f(x)在区间(1,2)上单调递增
B.函数y=f(x)的图像关于直线x=2对称
C.若x1≠x2,但f(x1)=f(x2),则x1+x2=4
D.函数f(x)有且仅有两个零点
三、填空题(本题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.设f(x)=则f(f(2))=________.
14.计算:+log2=________.
15.不等式x>的解集为________.
16.的值是________.
四、解答题(本题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(10分)计算:(1);
(2)÷100-+7log714.
18.(12分)已知函数f(x)=.
(1)求f(x)的单调区间;
(2)若f(x)的最大值等于,求a的值.
19.(12分)已知f(x)=log2(1+x)+log2(1-x).
(1)求函数f(x)的定义域.
(2)判断函数f(x)的奇偶性,并加以说明.
(3)求f的值.
20.(12分)函数f(x)=ax(a>0,且a≠1)在[1,2]上的最大值比最小值大,求a的值.
21.(12分)已知函数f(x)=a3-ax(a>0且a≠1).
(1)当a=2时,f(x)<4,求x的取值范围.
(2)若f(x)在[0,1]上的最小值大于1,求a的取值范围.
22.(12分)某工厂因排污比较严重,决定着手整治,一个月时污染度为60,整治后前四月的污染度如下表:
月数 1 2 3 4 …
污染度 60 31 13 0 …
污染度为0后,该工厂即停止整治,污染度又开始上升,现用下列三个函数模拟从整治后第一个月开始工厂的污染模式:
f(x)=20|x-4|(x≥1),g(x)=(x-4)2(x≥1),h(x)=30|log2x-2|(x≥1),其中x表示月数,f(x),g(x),h(x)分别表示污染度.
(1)选用哪个函数模拟比较合理,并说明理由;
(2)若以比较合理的模拟函数预测,整治后有多少个月的污染度不超过60
章末质量检测(四) 指数函数、对数函数与幂函数
1.解析:因为lg9<lg10=1,所以=1-lg9.
答案:B
2.解析:由得x>2且x≠3,故选C.
答案:C
3.解析:∵3x+1>1,∴0<<1,∴函数值域为(0,1).
答案:B
4.解析:f(x)=logax,∵f(2)=1,∴loga2=1.∴a=2.
∴f(x)=log2x.
答案:A
5.解析:设幂函数的解析式为y=xα,∵幂函数y=f(x)的图像过点(4,2),∴2=4α,解得α=.∴y=,其定义域为[0,+∞),且是增函数.当0
6.解析:因为3b=5,所以b=log35,log3=log330=(log33+log32+log35)
=(1+a+b).
答案:A
7.解析:c=只需比较log23.4,log43.6,log3的大小,又0<log43.6<1,log23.4>log33.4>log3>1,所以a>c>b.
答案:C
8.解析:方法一 当a>1时,y=xa与y=logax均为增函数,但y=xa递增较快,排除C;当0<a<1时,y=xa为增函数,y=logax为减函数,排除A.由于y=xa递增较慢,所以选D.
方法二 幂函数f(x)=xa的图像不过(0,1)点,故A错;B项中由对数函数f(x)=logax的图像知0<a<1,而此时幂函数f(x)=xa的图像应是增长越来越慢的变化趋势,故B错,D对;C项中由对数函数f(x)=logax的图像知a>1,而此时幂函数f(x)=xa的图像应是增长越来越快的变化趋势,故C错.
答案:D
9.解析:对于A,α=-1时幂函数y=x-1在(-∞,0)和(0,+∞)是减函数,在其定义域上不是减函数,A错误;对于B,α=0时幂函数y=x0=1(x≠0),其图像是一条直线,去掉点(0,1),B错误;对于C,α=2时幂函数y=x2在定义域R上是偶函数,C正确;对于D,α=3时幂函数y=x3在R上的奇函数,且是增函数,有唯一零点是0,D正确.
答案:CD
10.解析:因为0
又因为0
答案:BD
11.解析:=,所以A成立,×≠,所以B不成立,函数f(x)=2x,在R上是单调递增函数,若x1>x2则f(x1)>f(x2),则>0,若x1
答案:ACD
12.解析:函数f(x)=|ln|2-x||的图像如图所示:
由图可得:函数f(x)在区间(1,2)上单调递增,A正确;函数y=f(x)的图像关于直线x=2对称,B正确;若x1≠x2,但f(x1)=f(x2),则当x1,x2>2时,x1+x2>4,C错误;函数f(x)有且仅有两个零点,D正确.
答案:ABD
13.解析:因为f(2)=log3(22-1)=1,
所以f(f(2))=f(1)=2e1-1=2.
答案:2
14.解析:原式=|log25-2|+log25-1=log25-2-log25=-2.
答案:-2
15.解析:不等式>可化为-2x>,等价于x2-2x
答案:
17.解析:(1)原式=-1-++[()-4]-=-1-++()3=+2=.
(2)原式=-(lg4+lg25)÷100-+14=-2÷10-1+14=-20+14=-6.
18.解析:(1)令t=|x|-a,则f(x)=,
不论a取何值,t在(-∞,0]上单调递减,在[0,+∞)上单调递增,
又y=是单调递减的,
因此f(x)的单调递增区间是(-∞,0],
单调递减区间是[0,+∞).
(2)由于f(x)的最大值是,且=,
所以g(x)=|x|-a应该有最小值-2,
从而a=2.
19.解析:(1)由得
即-1
因为函数f(x)的定义域为{x|-1
所以函数f(x)=log2(1+x)+log2(1-x)为偶函数.
(3)f=log2+log2
=log2
=log2=log2=-1.
20.解析:分情况讨论:
①当0<a<1时,函数f(x)=ax(a>0,且a≠1)在[1,2]上的最大值f(x)max=f(1)=a1=a,最小值f(x)min=f(2)=a2,
∴a-a2=,解得a=或a=0(舍去);
②当a>1时,函数f(x)=ax(a>0,且a≠1)在[1,2]上的最大值f(x)max=f(2)=a2,最小值f(x)min=f(1)=a1=a,
∴a2-a=,解得a=或a=0(舍去).
综上所述,a=或a=.
21.解析:(1)当a=2时,f(x)=23-2x<4=22,3-2x<2,得x>.
(2)y=3-ax在定义域内单调递减,
当a>1时,函数f(x)在[0,1]上单调递减,f(x)min=f(1)=a3-a>1=a0,得1
综上:1
因为f(2)=40,g(2)≈26.7,
h(2)=30,f(3)=20,g(3)≈6.7,h(3)≈12.5,
由此可得h(x)更接近实际值,
所以用h(x)模拟比较合理.
(2)因为h(x)=30|log2x-2|在x≥4时是增函数,
又因为h(16)=60,故整治后有16个月的污染度不超过60.
9
