青岛版九年级数学下册 5.6 二次函数的图象与一元二次方程 课件(共17张PPT)
文档属性
| 名称 | 青岛版九年级数学下册 5.6 二次函数的图象与一元二次方程 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-14 07:09:16 | ||
图片预览



文档简介
(共17张PPT)
5.6 二次函数的图象与一元二次方程(1)
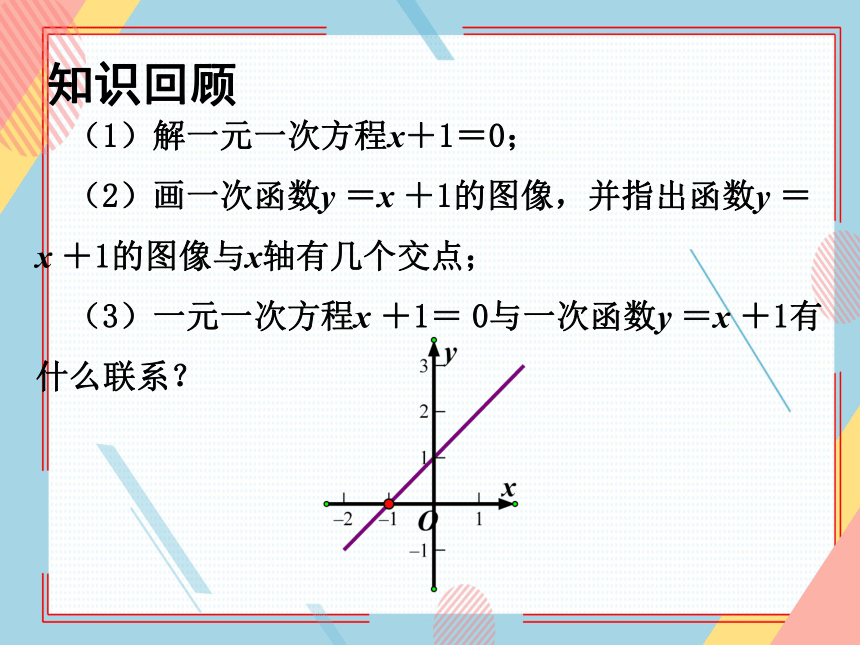
(1)解一元一次方程x+1=0;
(2)画一次函数y =x +1的图像,并指出函数y = x +1的图像与x轴有几个交点;
(3)一元一次方程x +1= 0与一次函数y =x +1有什么联系?
知识回顾
打高尔夫球时,球的飞行路线可以看成是一条抛物线,如果不考虑空气的阻力,某次球的飞行高度 y(单位:米)与飞行距离 x(单位:百米)满足二次函数 :y= -5x2 + 20x,这个球飞行的水平距离最远是多少米?
y(米)
x(百米)
4
1
2
3
A
o
10
情境创设
y=x2+2x
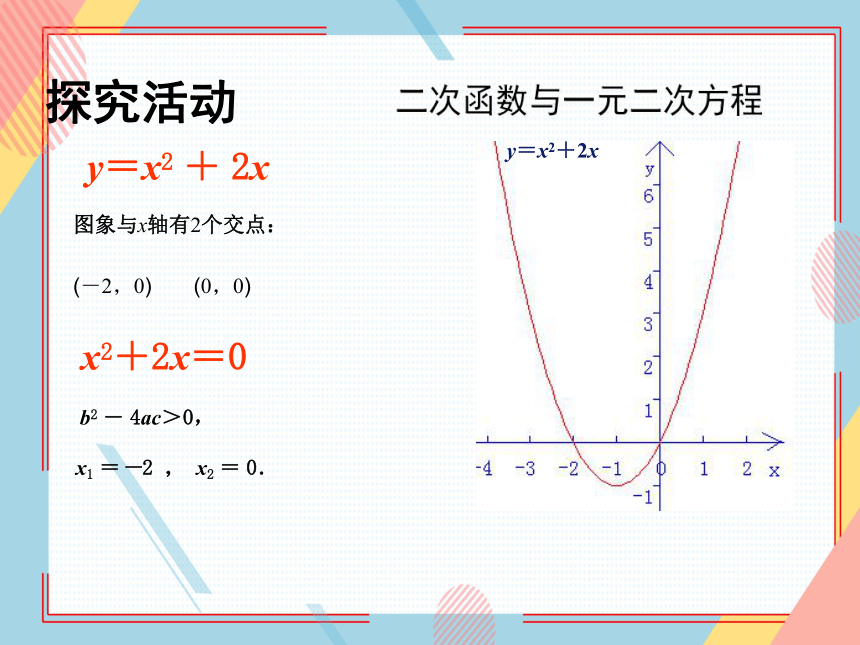
y=x2 + 2x
图象与x轴有2个交点:
(-2,0) (0,0)
x2+2x=0
b2 - 4ac>0,
x1 =-2 , x2 = 0.
二次函数与一元二次方程
y=x2+2x
探究活动
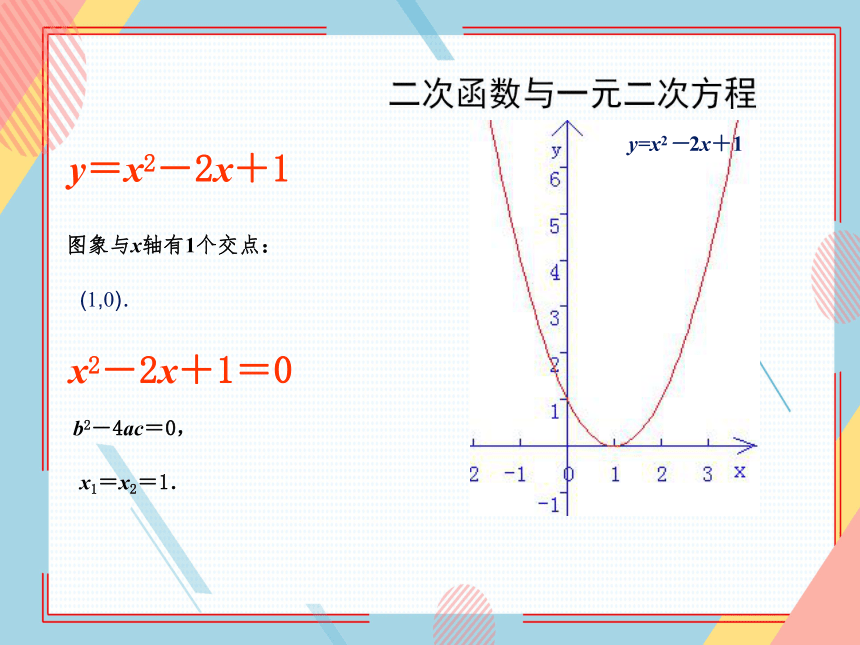
y=x2-2x+1
图象与x轴有1个交点:
(1,0).
x2-2x+1=0
y=x2-2x+1
二次函数与一元二次方程
b2-4ac=0,
x1=x2=1.
y=x2-2x+2
图象与x轴没有交点.
x2-2x+2=0
y=x2-2x+2
没有实数根.
二次函数与一元二次方程
b2-4ac<0,
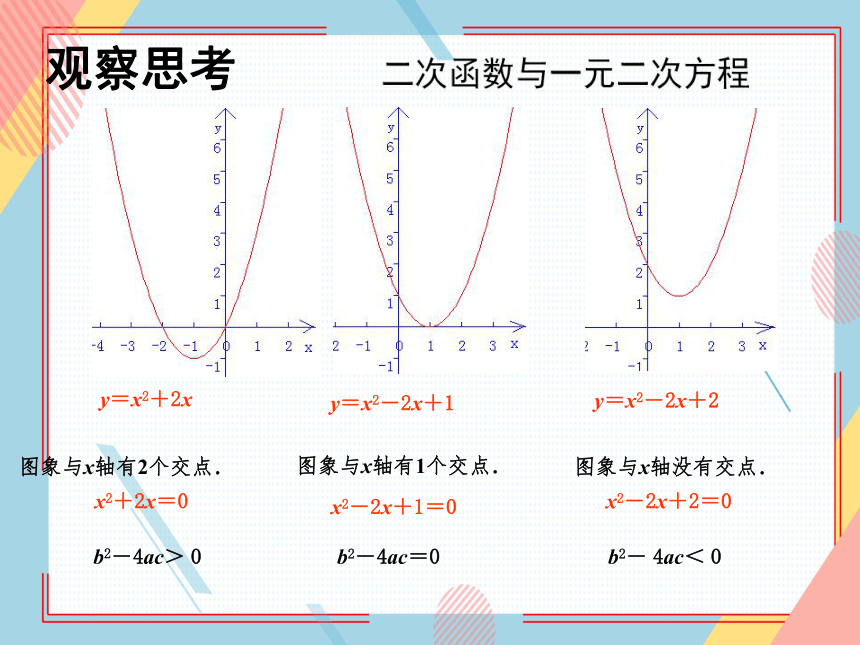
y=x2+2x
图象与x轴有2个交点.
x2+2x=0
y=x2-2x+1
图象与x轴有1个交点.
x2-2x+1=0
y=x2-2x+2
图象与x轴没有交点.
x2-2x+2=0
b2-4ac=0
b2-4ac> 0
b2- 4ac< 0
二次函数与一元二次方程
观察思考
y=x2+2x
x2+2x=0
y=x2-2x+1
x2-2x+1=0
y=x2-2x+2
x2-2x+2=0
(-2,0) (0,0)
(1,0)
图象与x轴没有交点.
没有实数根.
二次函数与一元二次方程
x1=-2 ,x2= 0
x1=x2 =1
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
①有两个交点,
②有一个交点,
③没有交点.
当二次函数y=ax2+bx+c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x 的值,即一元二次方程ax2+bx+c=0的根.
二次函数与一元二次方程
归纳总结
抛物线y=ax2 + bx + c
抛物线 y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况说明:
1.b2-4ac>0 一元二次方程ax2 + bx+c=0有两个不等的实数根.
与x轴有两个交点.
抛物线y = ax2 + bx + c
2. b2-4ac=0 一元二次方程ax2 + bx + c = 0
与x轴有唯一公共点.
抛物线y=ax2 + bx + c
3. b2-4ac<0 一元二次方程ax2 + bx + c=0
与x轴没有公共点.
没有实数根.
有两个相等的实数根.
归纳总结
不画图像,你能判断函数
的图象与x轴是否有公共点?请说明理由.
根据一元二次方程的根的情况,可以知道二次函数的图象与x轴的公共点的个数.
已知二次函数y=x2-4x+k+2与x轴有公共点,求k的取值范围.
例题讲解
打高尔夫球时,球的飞行路线可以看成是一条抛物线,如果不考虑空气的阻力,球的飞行高度y(单位:米)与飞行距离x(单位:百米)之间具有关系:y=-5x2 + 20x,想一想:球的飞行高度能否达到40m?
O
y(米)
x(百米)
4
1
2
3
40
10
拓展延伸
1. 方程 的根是 ;则函数
的图像与x轴的交点有 个,其坐标是 .
-5,1
2
(-5,0)、(1,0)
随堂练习
2. 方程 的根是 ;则函数 的图像与x轴的交点有_ 个,其坐标是 .
3.下列函数的图像中,与x轴没有公共点的是( )
1
(5,0)
D
A.
C.
B.
D.
5.6 二次函数的图象与一元二次方程(1)
(1)解一元一次方程x+1=0;
(2)画一次函数y =x +1的图像,并指出函数y = x +1的图像与x轴有几个交点;
(3)一元一次方程x +1= 0与一次函数y =x +1有什么联系?
知识回顾
打高尔夫球时,球的飞行路线可以看成是一条抛物线,如果不考虑空气的阻力,某次球的飞行高度 y(单位:米)与飞行距离 x(单位:百米)满足二次函数 :y= -5x2 + 20x,这个球飞行的水平距离最远是多少米?
y(米)
x(百米)
4
1
2
3
A
o
10
情境创设
y=x2+2x
y=x2 + 2x
图象与x轴有2个交点:
(-2,0) (0,0)
x2+2x=0
b2 - 4ac>0,
x1 =-2 , x2 = 0.
二次函数与一元二次方程
y=x2+2x
探究活动
y=x2-2x+1
图象与x轴有1个交点:
(1,0).
x2-2x+1=0
y=x2-2x+1
二次函数与一元二次方程
b2-4ac=0,
x1=x2=1.
y=x2-2x+2
图象与x轴没有交点.
x2-2x+2=0
y=x2-2x+2
没有实数根.
二次函数与一元二次方程
b2-4ac<0,
y=x2+2x
图象与x轴有2个交点.
x2+2x=0
y=x2-2x+1
图象与x轴有1个交点.
x2-2x+1=0
y=x2-2x+2
图象与x轴没有交点.
x2-2x+2=0
b2-4ac=0
b2-4ac> 0
b2- 4ac< 0
二次函数与一元二次方程
观察思考
y=x2+2x
x2+2x=0
y=x2-2x+1
x2-2x+1=0
y=x2-2x+2
x2-2x+2=0
(-2,0) (0,0)
(1,0)
图象与x轴没有交点.
没有实数根.
二次函数与一元二次方程
x1=-2 ,x2= 0
x1=x2 =1
二次函数y=ax2+bx+c的图象和x轴交点有三种情况:
①有两个交点,
②有一个交点,
③没有交点.
当二次函数y=ax2+bx+c的图象和x轴有交点时,交点的横坐标就是当y=0时自变量x 的值,即一元二次方程ax2+bx+c=0的根.
二次函数与一元二次方程
归纳总结
抛物线y=ax2 + bx + c
抛物线 y=ax2+bx+c与x轴的交点个数可由一元二次方程ax2+bx+c=0的根的情况说明:
1.b2-4ac>0 一元二次方程ax2 + bx+c=0有两个不等的实数根.
与x轴有两个交点.
抛物线y = ax2 + bx + c
2. b2-4ac=0 一元二次方程ax2 + bx + c = 0
与x轴有唯一公共点.
抛物线y=ax2 + bx + c
3. b2-4ac<0 一元二次方程ax2 + bx + c=0
与x轴没有公共点.
没有实数根.
有两个相等的实数根.
归纳总结
不画图像,你能判断函数
的图象与x轴是否有公共点?请说明理由.
根据一元二次方程的根的情况,可以知道二次函数的图象与x轴的公共点的个数.
已知二次函数y=x2-4x+k+2与x轴有公共点,求k的取值范围.
例题讲解
打高尔夫球时,球的飞行路线可以看成是一条抛物线,如果不考虑空气的阻力,球的飞行高度y(单位:米)与飞行距离x(单位:百米)之间具有关系:y=-5x2 + 20x,想一想:球的飞行高度能否达到40m?
O
y(米)
x(百米)
4
1
2
3
40
10
拓展延伸
1. 方程 的根是 ;则函数
的图像与x轴的交点有 个,其坐标是 .
-5,1
2
(-5,0)、(1,0)
随堂练习
2. 方程 的根是 ;则函数 的图像与x轴的交点有_ 个,其坐标是 .
3.下列函数的图像中,与x轴没有公共点的是( )
1
(5,0)
D
A.
C.
B.
D.
