北师大版八年级数学下册 第二章《一元一次不等式与一元一次不等式组》回顾与思考 课件(共29张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 第二章《一元一次不等式与一元一次不等式组》回顾与思考 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-14 10:46:55 | ||
图片预览






文档简介
(共29张PPT)
第二章 一元一次不等式与一元一次不等式组
(回顾与思考)
版 本:北京师范大学出版社
章 节:八年级下册 第二章
授 课:回顾与思考
1.通过梳理本章内容,进一步体会模型思想及类比的思想方法.
2.通过基础过关题组的训练,进一步夯实基础,掌握不等式的基本性质,理解不等式(组)的解及解集的含义,会解简单的一元一次不等式(组),并能在数轴上表示其解集,并体会不等式、函数、方程之间的联系.
3.通过深度研讨环节,能够举一反三,灵活应用.
4.通过实际应用,能够建立不等模型,能够用一元一次不等式解决一些简单的实际问题.
学习目标
课前以小组为单位制作思维导图,下面欣赏他们的成果,并请小组代表介绍制作思路,并对照自己的思维导图,有哪些优缺点.
制作思维导图的要点:有明确的中心主题
有清晰的结构关系
有明了的关键词
有充实的内容
合作探究
牛晨晨
陈乐源
王雨洁
耿鑫欣
王安南
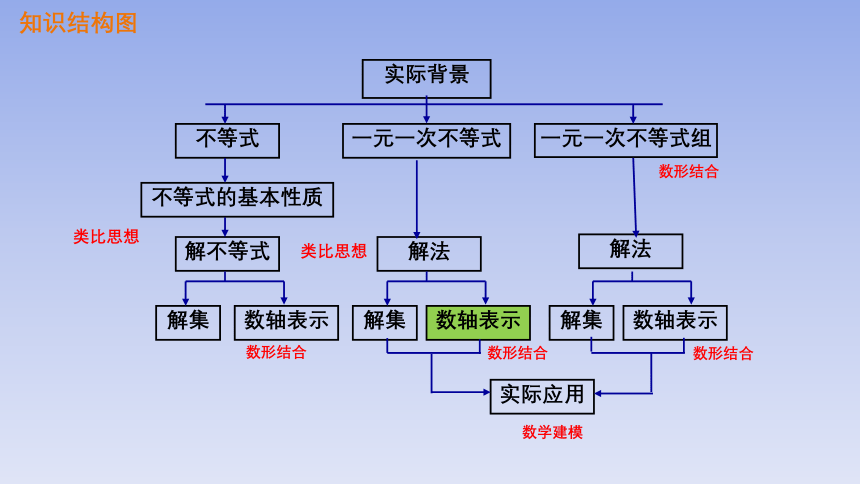
实际背景
不等式
一元一次不等式
一元一次不等式组
不等式的基本性质
解不等式
解法
解法
解集
数轴表示
解集
解集
数轴表示
数轴表示
实际应用
数形结合
数形结合
数形结合
数形结合
类比思想
类比思想
数学建模
知识结构图
要求:独立完成基础过关习题
时间:5分钟
评价方式:自评
1.C 2.C 3.A 4.B 5.x<2 6.x<2 7.C 8.(1,0) 9.x≥1
基础过关
1.给出下面6个式子:①3>0;②x<-2;③4x+3y≠0;④x=3;⑤x-1;⑥x+2≤3. 其中不等式有( )
A.2个 B.3个
C.4个 D.5个
C
基础过关
2.有下列四个命题:①若a>b,则a+1>b+1;②若a>b,则a-1>b-1;③若a>b,则-2a<-2b;④若a>b,则ma<mb. 其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.若x>y,且(a-3)x<(a-3)y,则a的值可能是( )
A.0 B.3 C.4 D.5
C
A
基础过关
4.下列不等式中,是一元一次不等式的有( )
①3x-7>0; ②2x+y>3;
③2x2-x>2x2-1; ④x+1<7.
A.1个 B.2个 C.3个 D.4个
B
基础过关
问题二:解下列不等式(组)
5.解下列不等式 6.解下列不等式组,并在数轴
表示不等式组的解集.
解: 去分母:
移项:
合并同类项:
系数化为1:
①②
解:解不等式①得:
解不等式②得:x<2
所以原不等式组的解集为x<2.
解一元一次不等式步骤:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)系数化成1.
解一元一次不等式组步骤:
(1)分别解出各不等式;
(2)在数轴上表示各不等式的解集;
(3)找出各解集的公共部分;
(4)写出解集.
基础过关
问题三:一元一次不等式与一次函数的关系
7.一次函数y=kx+b的图象如图所示,当y>0时,x的取值范围是( )
A.x<0 B.x>0 C.x<2 D.x>2
8.若关于x的不等式mx-1>0(m≠0)的解集是x>1,
则直线y=mx-1与x轴的交点坐标是________.
C
(1,0)
基础过关
9.如图,直线y=3x和y=kx+2相交于点P(a,3),则不等式3x≥kx+2的解集为________.
总结归纳:找交点
比高点
定范围
x≥1
基础过关
要求:先独立思考,再小组交流
时间:时间8分钟
评价方式:小组互评
10.m=2,n=-1 1
11.112.(1)a ≤2
(2)a >2
深度研讨
问题四:含参数的不等式综合问题
10.已知不等式组 的解集为 ,求
的值.
深度研讨
11.若不等式x-2归纳:解不等式(组)
画数轴,定范围
验临界点
深度研讨
12.已知不等式组
(1)如果此不等式组无解,则a的取值范围_______;
(2)如果此不等式组有解,则a的取值范围________.
不等式组解集口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).
a ≤2
a >2
深度研讨
要求:先独立思考,再组内交流
时间:5分钟
评价方式:小组派代表分享
实际应用
13.小丽去文具店买铅笔和橡皮,铅笔每支0.5元,橡皮每块0.4元,
小丽带了2元钱,可以买几支铅笔、几块橡皮?
实际应用
14.甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超过300元时,超出部分按原价的8折付款;在乙超市累计购买商品超过250元时,超出部分按原价的8.5折付款.设一顾客预计购物x(x>300)元.
(1)分别写出该顾客在甲、乙两家超市购物所付的费用y甲(元),y乙(元)与x之间的函数关系式;
(2)该顾客到哪家超市购物更优惠?
实际应用
解:(1)在甲超市购物所付的费用:
y甲=300+0.8×(x-300)=0.8x+60;
在乙超市购物所付的费用:
y乙=250+0.85×(x-250)=0.85x+37.5.
实际应用
(2)由y甲=y乙,得0.8x+60=0.85x+37.5,解得x=450,
∴当x=450时,在甲、乙两超市购物所付费用一样;
由y甲>y乙,得0.8x+60>0.85x+37.5,
解得x<450,
∴当300<x<450时,到乙超市购物更优惠;
由y甲<y乙,得0.8x+60<0.85x+37.5,解得x>450,
∴当x>450时,到甲超市购物更优惠.
实际应用
不等式及其性质
用数轴表示不等式组解集
一元一次不等式与一次函数的关系
一元一次不等式组及其解法
一元一次不等式及其解法
实际应用
从今天的课程中,
你学到了哪些知识?
掌握了哪些方法?
还有哪些困惑?
课堂感悟
1.C 2.B 3.B 4. 10 5.x<3 6.12
要求:独立完成
时间:5分钟
评价方式同学互评与教师评价相结合
当堂检测
内容 达成目标 其他
归纳知识结构 ☆☆☆☆☆
基础过关 ☆☆☆☆☆
深度研讨 ☆☆☆☆☆
实际应用 ☆☆☆☆☆
本节课你的学习目标达成了吗?如果没有那么你能得到几颗星星呢?
自我评价
1.必做:完成课本61页复习题第2、4、7、9、12题(AB组全做)
2.选做:完成课本63页复习题第13、15题(B组做)
课后作业
第二章 一元一次不等式与一元一次不等式组
(回顾与思考)
版 本:北京师范大学出版社
章 节:八年级下册 第二章
授 课:回顾与思考
1.通过梳理本章内容,进一步体会模型思想及类比的思想方法.
2.通过基础过关题组的训练,进一步夯实基础,掌握不等式的基本性质,理解不等式(组)的解及解集的含义,会解简单的一元一次不等式(组),并能在数轴上表示其解集,并体会不等式、函数、方程之间的联系.
3.通过深度研讨环节,能够举一反三,灵活应用.
4.通过实际应用,能够建立不等模型,能够用一元一次不等式解决一些简单的实际问题.
学习目标
课前以小组为单位制作思维导图,下面欣赏他们的成果,并请小组代表介绍制作思路,并对照自己的思维导图,有哪些优缺点.
制作思维导图的要点:有明确的中心主题
有清晰的结构关系
有明了的关键词
有充实的内容
合作探究
牛晨晨
陈乐源
王雨洁
耿鑫欣
王安南
实际背景
不等式
一元一次不等式
一元一次不等式组
不等式的基本性质
解不等式
解法
解法
解集
数轴表示
解集
解集
数轴表示
数轴表示
实际应用
数形结合
数形结合
数形结合
数形结合
类比思想
类比思想
数学建模
知识结构图
要求:独立完成基础过关习题
时间:5分钟
评价方式:自评
1.C 2.C 3.A 4.B 5.x<2 6.x<2 7.C 8.(1,0) 9.x≥1
基础过关
1.给出下面6个式子:①3>0;②x<-2;③4x+3y≠0;④x=3;⑤x-1;⑥x+2≤3. 其中不等式有( )
A.2个 B.3个
C.4个 D.5个
C
基础过关
2.有下列四个命题:①若a>b,则a+1>b+1;②若a>b,则a-1>b-1;③若a>b,则-2a<-2b;④若a>b,则ma<mb. 其中正确的有( )
A.1个 B.2个 C.3个 D.4个
3.若x>y,且(a-3)x<(a-3)y,则a的值可能是( )
A.0 B.3 C.4 D.5
C
A
基础过关
4.下列不等式中,是一元一次不等式的有( )
①3x-7>0; ②2x+y>3;
③2x2-x>2x2-1; ④x+1<7.
A.1个 B.2个 C.3个 D.4个
B
基础过关
问题二:解下列不等式(组)
5.解下列不等式 6.解下列不等式组,并在数轴
表示不等式组的解集.
解: 去分母:
移项:
合并同类项:
系数化为1:
①②
解:解不等式①得:
解不等式②得:x<2
所以原不等式组的解集为x<2.
解一元一次不等式步骤:
(1)去分母;
(2)去括号;
(3)移项;
(4)合并同类项;
(5)系数化成1.
解一元一次不等式组步骤:
(1)分别解出各不等式;
(2)在数轴上表示各不等式的解集;
(3)找出各解集的公共部分;
(4)写出解集.
基础过关
问题三:一元一次不等式与一次函数的关系
7.一次函数y=kx+b的图象如图所示,当y>0时,x的取值范围是( )
A.x<0 B.x>0 C.x<2 D.x>2
8.若关于x的不等式mx-1>0(m≠0)的解集是x>1,
则直线y=mx-1与x轴的交点坐标是________.
C
(1,0)
基础过关
9.如图,直线y=3x和y=kx+2相交于点P(a,3),则不等式3x≥kx+2的解集为________.
总结归纳:找交点
比高点
定范围
x≥1
基础过关
要求:先独立思考,再小组交流
时间:时间8分钟
评价方式:小组互评
10.m=2,n=-1 1
11.1
(2)a >2
深度研讨
问题四:含参数的不等式综合问题
10.已知不等式组 的解集为 ,求
的值.
深度研讨
11.若不等式x-2
画数轴,定范围
验临界点
深度研讨
12.已知不等式组
(1)如果此不等式组无解,则a的取值范围_______;
(2)如果此不等式组有解,则a的取值范围________.
不等式组解集口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).
a ≤2
a >2
深度研讨
要求:先独立思考,再组内交流
时间:5分钟
评价方式:小组派代表分享
实际应用
13.小丽去文具店买铅笔和橡皮,铅笔每支0.5元,橡皮每块0.4元,
小丽带了2元钱,可以买几支铅笔、几块橡皮?
实际应用
14.甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超过300元时,超出部分按原价的8折付款;在乙超市累计购买商品超过250元时,超出部分按原价的8.5折付款.设一顾客预计购物x(x>300)元.
(1)分别写出该顾客在甲、乙两家超市购物所付的费用y甲(元),y乙(元)与x之间的函数关系式;
(2)该顾客到哪家超市购物更优惠?
实际应用
解:(1)在甲超市购物所付的费用:
y甲=300+0.8×(x-300)=0.8x+60;
在乙超市购物所付的费用:
y乙=250+0.85×(x-250)=0.85x+37.5.
实际应用
(2)由y甲=y乙,得0.8x+60=0.85x+37.5,解得x=450,
∴当x=450时,在甲、乙两超市购物所付费用一样;
由y甲>y乙,得0.8x+60>0.85x+37.5,
解得x<450,
∴当300<x<450时,到乙超市购物更优惠;
由y甲<y乙,得0.8x+60<0.85x+37.5,解得x>450,
∴当x>450时,到甲超市购物更优惠.
实际应用
不等式及其性质
用数轴表示不等式组解集
一元一次不等式与一次函数的关系
一元一次不等式组及其解法
一元一次不等式及其解法
实际应用
从今天的课程中,
你学到了哪些知识?
掌握了哪些方法?
还有哪些困惑?
课堂感悟
1.C 2.B 3.B 4. 10 5.x<3 6.12
要求:独立完成
时间:5分钟
评价方式同学互评与教师评价相结合
当堂检测
内容 达成目标 其他
归纳知识结构 ☆☆☆☆☆
基础过关 ☆☆☆☆☆
深度研讨 ☆☆☆☆☆
实际应用 ☆☆☆☆☆
本节课你的学习目标达成了吗?如果没有那么你能得到几颗星星呢?
自我评价
1.必做:完成课本61页复习题第2、4、7、9、12题(AB组全做)
2.选做:完成课本63页复习题第13、15题(B组做)
课后作业
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
