2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.3.1二项式定理课件(共28张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.3.1二项式定理课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-13 15:09:42 | ||
图片预览


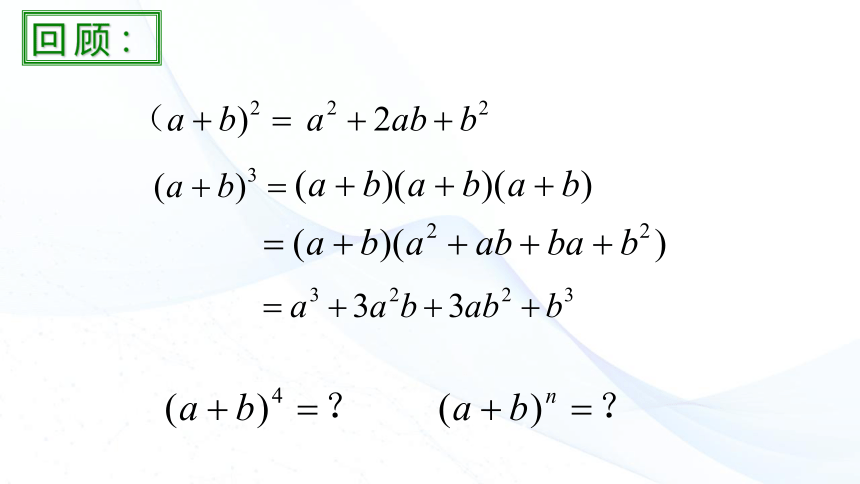






文档简介
问题:
(1)今天是星期一,那么7天后的这一天是星期几呢?
(3)如果是 天后的这一天呢?
(2)如果是15天后的这一天呢?
(星期二)
(星期一)
二项式定理
F佳
2022年04月
回顾:
②各项中a与b次数之和呈现什么规律?
①在以上各展开式中各有多少项?
③各项的系数是什么?
重点关注
(a+b)2=(a+b)(a+b)
=a×a+a×b+b×a+b×b
=a2+2ab+b2
从上述过程可以看到,(a+b)2是2个(a+b)相乘,根据多项式乘法法则,每个(a+b)在相乘时有两种选择,选a或选b,而且每个(a+b)中的a或b都选定后,才能得到展开式的一项.
于是,由分步乘法计数原理,在合并同类项之前,(a+b)2的展开式共有2×2=22项,而且每一项都是a2-k×bk (k=0,1,2)的形式.
项的形式:
2个(a+b)都不选b得到的,因此a2出现的次数相当于从2个(a+b)中取0个b(即都取a)的组合数 ,即a2只有1个;
由1个(a+b)中选a,另1个(a+b)中选b得到的.由于b选定后,a的选法也随之确定,因此,ab出现的次数相当于从2个(a+b)中取1个b的组合数 ,即ab共有2个.
考虑b
项的形式:
考虑b
由2个(a+b)中都选b得到的.因此,b2出现的次数相当于从2个(a+b)中取2个b的组合数 ,即b2只有1个.
(a+b)4= (a+b) (a+b) (a+b) (a+b)=?
问题:
1).(a+b)4展开后各项形式分别是什么?
2).你能分析说明各项前的系数吗?
a4 a3b a2b2 ab3 b4
(a+b)n=?
观察下面式子,你能猜想(a+b)n的展开式吗?
每个都不取b的情况有1种,即Cn0 ,则an前的系数为Cn0
恰有1个取b的情况有Cn1种,则an-1b前的系数为Cn1
恰有2个取b的情况有Cn2 种,则an-2b2前的系数为Cn2
......
恰有k个取b的情况有Cnk 种,则an-kbk前的系数为Cnk
......
恰有n个取b的情况有Cnn 种,则bn前的系数为Cnn
字母a按降幂排列,次数由n 递减到0;
字母b按升幂排列,次数由0递增到n.
2.系数规律:
2.指数规律:
(1)各项的次数均为n;即为n次齐次式
(2)a的次数由n逐次降到0,
b的次数由0逐次升到n.
1.项数规律:
展开式共有n+1个项
1.在二项式定理中,若设a=1, b=x,则得到公式
2、把b用-b代替
例1、
求 的展开式.
解:根据二项式定理,
课本P31 练习 1
1. 写出(????+????)5的展开式.
?
例2:(1) ①求 (1+2x)7 的展开式的第4项;
②求 (1+2x)7 的展开式的第4项的系数;
③求 (1+2x)7 的展开式的第4项的二项式系数.
解:
(1)
(2)求 (1+2x)7 的展开式的第4项的系数为280.
(3)求 (1+2x)7 的展开式的第4项的二项式系数为 .
注:1)注意对二项式定理的灵活应用
2)注意区别二项式系数与项的系数的概念
二项式系数:Cnr;
项的系数:二项式系数与数字系数的积
3)求二项式系数或项的系数的一种方法是将二项式展开
课本P31 练习 2
2.求(2a+3b)6的展开式的第3项.
课本P31 练习 4
4. (x-1)10的展开式的第6项的系数是( ).
(A)????106 (B)-????106 (C) ????105 (D)-????105
?
课本P31 练习 3
3.写出(3?????123????)????的展开式的第r+1项.
?
练习:思维辨析(对的打"√",错的打"×")
(1)(a+b)n展开式中共有n项. ( )
(2)在二项式定理中,交换a,b的顺序对各项无影响. ( )
(3)?????????????????????????????????是(a+b)n展开式中的第k项. ( )
(4)(a-b)n与(a+b)n的二项式展开式的二项式系数相同. ( )
?
解:
的展开式的通项为
根据题意,得
因此, x2的系数是
求 的展开式中 x2 的系数.
例2(2)
课本P31 练习 5
5.在(x-1)(x-2)(x-3)(x-4)(x-5)的展开式中,含x4的项的系数是_________________.
练习:(1)求二项式(2?????1????)6的展开式中第 6项的二项式系数和第6项的系数;
(2)求(?????1????)9的展开式中x3的系数.
?
作业:课本P34 习题6.3 6
今天是星期一,那么 天后
的这一天是星期几?
余数是1,所以这一天是星期二
问题探究:
本小节结束
F佳
2022年04月
(1)今天是星期一,那么7天后的这一天是星期几呢?
(3)如果是 天后的这一天呢?
(2)如果是15天后的这一天呢?
(星期二)
(星期一)
二项式定理
F佳
2022年04月
回顾:
②各项中a与b次数之和呈现什么规律?
①在以上各展开式中各有多少项?
③各项的系数是什么?
重点关注
(a+b)2=(a+b)(a+b)
=a×a+a×b+b×a+b×b
=a2+2ab+b2
从上述过程可以看到,(a+b)2是2个(a+b)相乘,根据多项式乘法法则,每个(a+b)在相乘时有两种选择,选a或选b,而且每个(a+b)中的a或b都选定后,才能得到展开式的一项.
于是,由分步乘法计数原理,在合并同类项之前,(a+b)2的展开式共有2×2=22项,而且每一项都是a2-k×bk (k=0,1,2)的形式.
项的形式:
2个(a+b)都不选b得到的,因此a2出现的次数相当于从2个(a+b)中取0个b(即都取a)的组合数 ,即a2只有1个;
由1个(a+b)中选a,另1个(a+b)中选b得到的.由于b选定后,a的选法也随之确定,因此,ab出现的次数相当于从2个(a+b)中取1个b的组合数 ,即ab共有2个.
考虑b
项的形式:
考虑b
由2个(a+b)中都选b得到的.因此,b2出现的次数相当于从2个(a+b)中取2个b的组合数 ,即b2只有1个.
(a+b)4= (a+b) (a+b) (a+b) (a+b)=?
问题:
1).(a+b)4展开后各项形式分别是什么?
2).你能分析说明各项前的系数吗?
a4 a3b a2b2 ab3 b4
(a+b)n=?
观察下面式子,你能猜想(a+b)n的展开式吗?
每个都不取b的情况有1种,即Cn0 ,则an前的系数为Cn0
恰有1个取b的情况有Cn1种,则an-1b前的系数为Cn1
恰有2个取b的情况有Cn2 种,则an-2b2前的系数为Cn2
......
恰有k个取b的情况有Cnk 种,则an-kbk前的系数为Cnk
......
恰有n个取b的情况有Cnn 种,则bn前的系数为Cnn
字母a按降幂排列,次数由n 递减到0;
字母b按升幂排列,次数由0递增到n.
2.系数规律:
2.指数规律:
(1)各项的次数均为n;即为n次齐次式
(2)a的次数由n逐次降到0,
b的次数由0逐次升到n.
1.项数规律:
展开式共有n+1个项
1.在二项式定理中,若设a=1, b=x,则得到公式
2、把b用-b代替
例1、
求 的展开式.
解:根据二项式定理,
课本P31 练习 1
1. 写出(????+????)5的展开式.
?
例2:(1) ①求 (1+2x)7 的展开式的第4项;
②求 (1+2x)7 的展开式的第4项的系数;
③求 (1+2x)7 的展开式的第4项的二项式系数.
解:
(1)
(2)求 (1+2x)7 的展开式的第4项的系数为280.
(3)求 (1+2x)7 的展开式的第4项的二项式系数为 .
注:1)注意对二项式定理的灵活应用
2)注意区别二项式系数与项的系数的概念
二项式系数:Cnr;
项的系数:二项式系数与数字系数的积
3)求二项式系数或项的系数的一种方法是将二项式展开
课本P31 练习 2
2.求(2a+3b)6的展开式的第3项.
课本P31 练习 4
4. (x-1)10的展开式的第6项的系数是( ).
(A)????106 (B)-????106 (C) ????105 (D)-????105
?
课本P31 练习 3
3.写出(3?????123????)????的展开式的第r+1项.
?
练习:思维辨析(对的打"√",错的打"×")
(1)(a+b)n展开式中共有n项. ( )
(2)在二项式定理中,交换a,b的顺序对各项无影响. ( )
(3)?????????????????????????????????是(a+b)n展开式中的第k项. ( )
(4)(a-b)n与(a+b)n的二项式展开式的二项式系数相同. ( )
?
解:
的展开式的通项为
根据题意,得
因此, x2的系数是
求 的展开式中 x2 的系数.
例2(2)
课本P31 练习 5
5.在(x-1)(x-2)(x-3)(x-4)(x-5)的展开式中,含x4的项的系数是_________________.
练习:(1)求二项式(2?????1????)6的展开式中第 6项的二项式系数和第6项的系数;
(2)求(?????1????)9的展开式中x3的系数.
?
作业:课本P34 习题6.3 6
今天是星期一,那么 天后
的这一天是星期几?
余数是1,所以这一天是星期二
问题探究:
本小节结束
F佳
2022年04月
