人教版数学七年级下册 5.9 平行线的性质课件 (共19张PPT)
文档属性
| 名称 | 人教版数学七年级下册 5.9 平行线的性质课件 (共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-14 17:26:50 | ||
图片预览





文档简介
(共19张PPT)
第五章 相交线与平行线
第8课时 平行线的性质(二)
目录
01
本课目标
02
课堂演练
1. 探索并证明两直线平行,同旁内角互补.
2. 能综合运用平行线的判定和性质解决问题.
两条平行线被第三条直线所截,同旁内角____________.
简单说成:两直线平行,同旁内角____________.
知识重点
知识点一 平行线的性质3
互补
互补
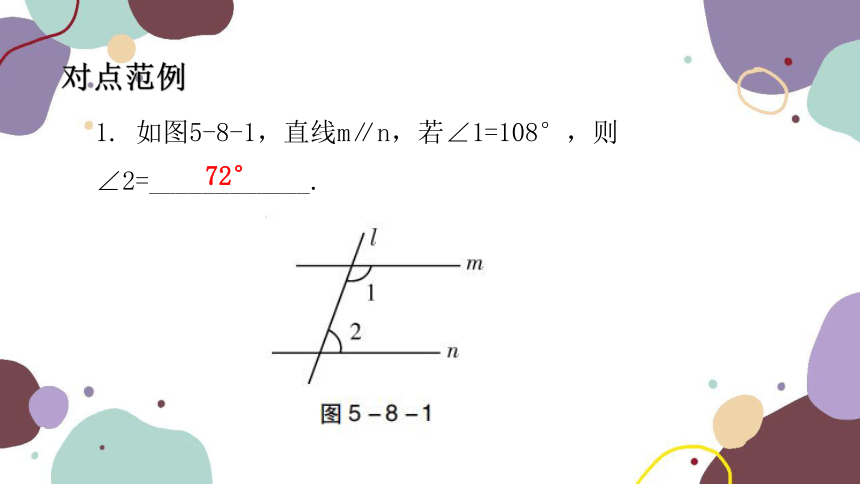
1. 如图5-8-1,直线m∥n,若∠1=108°,则∠2=____________.
对点范例
72°
平行线的判定是由角的数量关系来确定线的____________关系,而平行线的性质则是由线的位置关系来确定角的____________关系,因此,我们可以综合运用平行线的判定和性质进行计算或证明.
知识重点
知识点二 平行线的判定和性质的综合运用
位置
数量
2. 如图5-8-2,已知AD∥BC,BE平分∠ABC,若∠A=128°,则∠ADB的度数是( )
A. 40° B. 52°
C. 26° D. 34°
对点范例
C
对于出现一个或多个拐点的图形变化问题,都可以通过作____________线,利用平行线的性质求解.
知识重点
知识点三 平行线的拐点问题
平行
3. 如图5-8-3,m∥n,若∠1=110°,∠2=100°,则∠3=____________°.
对点范例
150
【例1】如图5-8-4,在四边形ABCD中,AB∥CD,∠D= ( )
A. 120° B. 135°
C. 145° D. 155°
思路点拨:找到对应的同旁内角,两角互补即可计算出结果.
典型例题
B
4. 如图5-8-5,已知AB∥CD,∠A=60°,∠ECD=120°,则∠ECA的度数是( )
A. 90°
B. 120°
C. 135°
D. 150°
举一反三
B
【例2】完成下面的证明:已知:如图5-8-6,AB∥CD,CD和BE相交于点O,DE平分∠CDF,DE和BE相交于点E,∠E=∠2. 求证:∠B=2∠2.
证明:∵∠E=∠2,
∴BE∥DF(_________________________).
∴∠CDF=∠____________(两直线平
行,同位角相等).
典型例题
内错角相等,两直线平行
1
又∵AB∥CD,
∴∠B=∠________(_________________________).
∴∠B=∠CDF.
∵DE平分∠CDF,
∴∠CDF=2∠_______.
∴∠B=2∠2.
思路点拨:综合运用平行线的判定与性质进行证明.
1
两直线平行,同位角相等
2
5. 如图5-8-7,已知EF∥AD,∠1=∠2,∠BAC=70°. 求∠AGD的度数并把过程填写完整.
解:∵EF∥AD,
∴∠2=_________(_________________________).
又∵∠1=∠2,∴∠1=__________.
∴AB∥_______
(______________________________).
∴∠BAC+____________=180°
(_________________________________).
∵∠BAC=70°,∴∠AGD=____________.
举一反三
∠3
两直线平行,同位角相等
∠3
DG
内错角相等,两直线平行
∠AGD
两直线平行,同旁内角互补
110°
【例3】(创新题)(1)如图5-8-8①,AB∥CD,点P在AB与CD之间,连接AP,CP,求证:∠APC=∠A+∠C;
(2)如图5-8-8②,AB∥CD,点P,E在AB与CD之间,AE平分∠BAP,CE平分∠DCP.求证:∠APC=2∠AEC.
典型例题
证明:(1)答图5-8-1,过点P作PQ∥AB.
∵AB∥CD,∴CD∥PQ(平行于同一条直线的两条直线平行).
∴∠APQ=∠A,
∠CPQ=∠C(两直线平行,
内错角相等).
∴∠APC=∠APQ+∠CPQ=
∠A+∠C.
(2)∵AE平分∠BAP,CE平分∠DCP,
∴∠BAP=2∠EAB,∠DCP=2∠ECD.
由(1)可知∠AEC=∠BAE+∠ECD,∠APC=∠BAP+∠DCP.
∴∠APC=2∠BAE+2∠ECD=2(∠BAE+∠ECD)=2∠AEC.
思路点拨:(1)过点P作PQ∥AB,利用平行线的性质和判定易得结论;(2)通过(1)建模,利用(1)的结论和角平分线的性质解决(2)比较简便.
6. (创新题)已知直线MN分别与直线AB,CD相交于点E,F,且∠AEM+∠DFM=180°.
(1)如图5-8-9①,求证:AB∥CD;
举一反三
(1)证明:∵∠AEM+∠DFM=180°,
∠AEM=∠BEF,
∴∠BEF+∠DFM=180°.
∴AB∥CD(同旁内角互补,两直线平行).
(2)如图5-8-9②,若点P在直线AB,CD之间,连接EP,FP.若∠AEP=35°,∠P=50°,试求∠CFP的度数.
(2)解:如答图5-8-2,过点P作PQ∥AB.
∵AB∥CD,∴CD∥PQ(平行于同一条直线的两条直线平行).
∴∠AEP=∠EPQ,∠CFP=∠FPQ(两直线平行,内错角相等)
∴∠EPF=∠EPQ+∠FPQ=∠AEP+∠CFP.
∵∠AEP=35°,∠EPF=50°,
∴∠CFP=50°-35°=15°,
即∠CFP的度数为15°.
谢 谢
第五章 相交线与平行线
第8课时 平行线的性质(二)
目录
01
本课目标
02
课堂演练
1. 探索并证明两直线平行,同旁内角互补.
2. 能综合运用平行线的判定和性质解决问题.
两条平行线被第三条直线所截,同旁内角____________.
简单说成:两直线平行,同旁内角____________.
知识重点
知识点一 平行线的性质3
互补
互补
1. 如图5-8-1,直线m∥n,若∠1=108°,则∠2=____________.
对点范例
72°
平行线的判定是由角的数量关系来确定线的____________关系,而平行线的性质则是由线的位置关系来确定角的____________关系,因此,我们可以综合运用平行线的判定和性质进行计算或证明.
知识重点
知识点二 平行线的判定和性质的综合运用
位置
数量
2. 如图5-8-2,已知AD∥BC,BE平分∠ABC,若∠A=128°,则∠ADB的度数是( )
A. 40° B. 52°
C. 26° D. 34°
对点范例
C
对于出现一个或多个拐点的图形变化问题,都可以通过作____________线,利用平行线的性质求解.
知识重点
知识点三 平行线的拐点问题
平行
3. 如图5-8-3,m∥n,若∠1=110°,∠2=100°,则∠3=____________°.
对点范例
150
【例1】如图5-8-4,在四边形ABCD中,AB∥CD,∠D= ( )
A. 120° B. 135°
C. 145° D. 155°
思路点拨:找到对应的同旁内角,两角互补即可计算出结果.
典型例题
B
4. 如图5-8-5,已知AB∥CD,∠A=60°,∠ECD=120°,则∠ECA的度数是( )
A. 90°
B. 120°
C. 135°
D. 150°
举一反三
B
【例2】完成下面的证明:已知:如图5-8-6,AB∥CD,CD和BE相交于点O,DE平分∠CDF,DE和BE相交于点E,∠E=∠2. 求证:∠B=2∠2.
证明:∵∠E=∠2,
∴BE∥DF(_________________________).
∴∠CDF=∠____________(两直线平
行,同位角相等).
典型例题
内错角相等,两直线平行
1
又∵AB∥CD,
∴∠B=∠________(_________________________).
∴∠B=∠CDF.
∵DE平分∠CDF,
∴∠CDF=2∠_______.
∴∠B=2∠2.
思路点拨:综合运用平行线的判定与性质进行证明.
1
两直线平行,同位角相等
2
5. 如图5-8-7,已知EF∥AD,∠1=∠2,∠BAC=70°. 求∠AGD的度数并把过程填写完整.
解:∵EF∥AD,
∴∠2=_________(_________________________).
又∵∠1=∠2,∴∠1=__________.
∴AB∥_______
(______________________________).
∴∠BAC+____________=180°
(_________________________________).
∵∠BAC=70°,∴∠AGD=____________.
举一反三
∠3
两直线平行,同位角相等
∠3
DG
内错角相等,两直线平行
∠AGD
两直线平行,同旁内角互补
110°
【例3】(创新题)(1)如图5-8-8①,AB∥CD,点P在AB与CD之间,连接AP,CP,求证:∠APC=∠A+∠C;
(2)如图5-8-8②,AB∥CD,点P,E在AB与CD之间,AE平分∠BAP,CE平分∠DCP.求证:∠APC=2∠AEC.
典型例题
证明:(1)答图5-8-1,过点P作PQ∥AB.
∵AB∥CD,∴CD∥PQ(平行于同一条直线的两条直线平行).
∴∠APQ=∠A,
∠CPQ=∠C(两直线平行,
内错角相等).
∴∠APC=∠APQ+∠CPQ=
∠A+∠C.
(2)∵AE平分∠BAP,CE平分∠DCP,
∴∠BAP=2∠EAB,∠DCP=2∠ECD.
由(1)可知∠AEC=∠BAE+∠ECD,∠APC=∠BAP+∠DCP.
∴∠APC=2∠BAE+2∠ECD=2(∠BAE+∠ECD)=2∠AEC.
思路点拨:(1)过点P作PQ∥AB,利用平行线的性质和判定易得结论;(2)通过(1)建模,利用(1)的结论和角平分线的性质解决(2)比较简便.
6. (创新题)已知直线MN分别与直线AB,CD相交于点E,F,且∠AEM+∠DFM=180°.
(1)如图5-8-9①,求证:AB∥CD;
举一反三
(1)证明:∵∠AEM+∠DFM=180°,
∠AEM=∠BEF,
∴∠BEF+∠DFM=180°.
∴AB∥CD(同旁内角互补,两直线平行).
(2)如图5-8-9②,若点P在直线AB,CD之间,连接EP,FP.若∠AEP=35°,∠P=50°,试求∠CFP的度数.
(2)解:如答图5-8-2,过点P作PQ∥AB.
∵AB∥CD,∴CD∥PQ(平行于同一条直线的两条直线平行).
∴∠AEP=∠EPQ,∠CFP=∠FPQ(两直线平行,内错角相等)
∴∠EPF=∠EPQ+∠FPQ=∠AEP+∠CFP.
∵∠AEP=35°,∠EPF=50°,
∴∠CFP=50°-35°=15°,
即∠CFP的度数为15°.
谢 谢
