湖南省2022年普通高中学业水平考试数学模拟试卷(六)(word版含答案)
文档属性
| 名称 | 湖南省2022年普通高中学业水平考试数学模拟试卷(六)(word版含答案) | 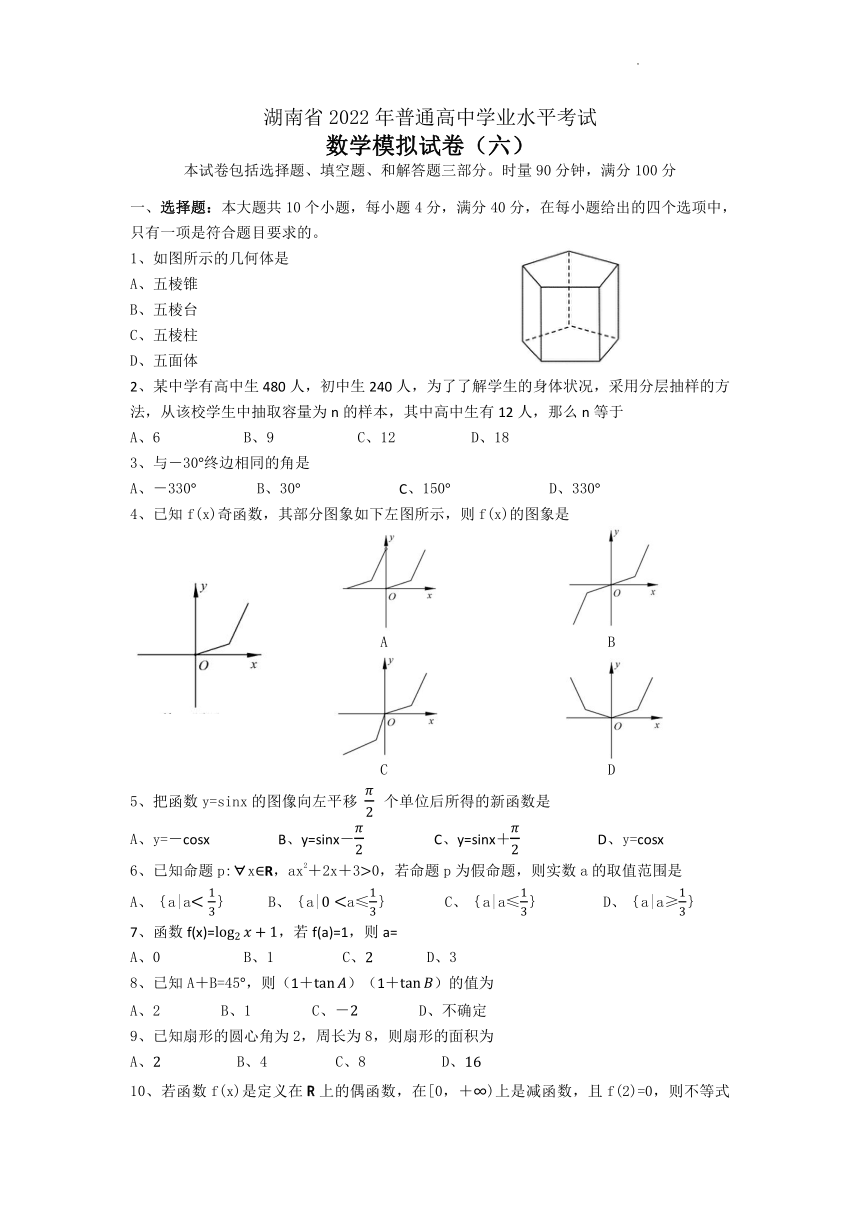 | |
| 格式 | doc | ||
| 文件大小 | 83.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-14 08:20:07 | ||
图片预览



文档简介
湖南省2022年普通高中学业水平考试
数学模拟试卷(六)
本试卷包括选择题、填空题、和解答题三部分。时量90分钟,满分100分
选择题:本大题共10个小题,每小题4分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1、如图所示的几何体是
A、五棱锥
B、五棱台
C、五棱柱
D、五面体
2、某中学有高中生480人,初中生240人,为了了解学生的身体状况,采用分层抽样的方法,从该校学生中抽取容量为n的样本,其中高中生有12人,那么n等于
A、6 B、9 C、12 D、18
3、与-30终边相同的角是
-330 B、30 C、150 D、330
已知f(x)奇函数,其部分图象如下左图所示,则f(x)的图象是
A B
C D
5、把函数y=sinx的图像向左平移 个单位后所得的新函数是
A、y=-cosx B、y=sinx- C、y=sinx+ D、y=cosx
6、已知命题p: xR,ax2+2x+30,若命题p为假命题,则实数a的取值范围是
A、{a|a} B、{a|a≤} C、{a|a≤} D、{a|a≥}
函数f(x)=,若f(a)=1,则a=
A、0 B、1 C、 D、3
8、已知A+B=45,则(1+)(1+)的值为
A、2 B、1 C、 D、不确定
9、已知扇形的圆心角为2,周长为8,则扇形的面积为
A、 B、4 C、8 D、
10、若函数f(x)是定义在R上的偶函数,在[0,+∞)上是减函数,且f(2)=0,则不等式f()0的解集是
A、( ,4) B、(0,)∪(4,+∞) C、(,2) D、(0,)∪(2,+∞)
填空题:本大题共5小题,每小题4分,满分20分。
已知集合A={1,2,a},B={1,3},若B A,则a=
采用简单随机抽样的方法,从含有5个个体的总体中抽取一个容量为2的样本,某个个体被抽到的概率为
数据3.2,3.6,4.5,2.4,4.6,6.4,7.8,7.9,8.0,8.1,8.4,8.6的75%分位数是
在长方体ABCD-A1B1C1D1中,与棱AA1垂直且异面的棱的条数是
如图所示,一学生在河岸紧靠河边笔直行走,在A处时,
经观察,在河对岸有一参照物C与学生前进方向成30°角,
学生前进200m后,测得该参照物与前进方向成75°角,则
河的宽度为 m.
解答题:本大题共4个小题,满分40分,解答应写出文字说明、证明过程或演算步骤 。
(本小题满分10分)
某初级中学共有学生2000名,各年级男、女生人数如下表:
年级 初一年级 初二年级 初三年级
女生 373 x y
男生 377 370 z
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求x的值;
(2)现用分层随机抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(3)在(2)中,若所抽取的初一年级、初二年级、初三年级三个年级学生的体重的平均数分别是40kg,50kg,60kg,估计该校所有学生体重的平均数.
(本小题满分10分)
已知不等式(x-a)(x-b) 0(其中ab)的解集为{x|-1x 2},函数f(x)=bx+a-2.
求a,b的值;
若函数f(x)的零点为x0,求x0和f(2x0)的值.
18、(本小题满分10分)
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,BC=3,BD=4,直线AD与平面BCD所成的角为45,点E,F分别是AC,AD的中点.
(1)求证:EF∥平面BCD;
(2)求三棱锥A-BCD的体积.
19、(本小题满分10分)
已知函数y=3sin(x-).
用“五点法”作函数的图象;
说出此图象是由y=sinx的图象经过怎样的变换得到的;
求此函数的对称轴、对称中心、单调递增区间。
参考答案
一、选择题
1-5 C D D B D 6-10 C B A B A
二、填空题
11. 3 12. 13.8.05 14.4 15.50( +1)
三、解答题
16.解:(1)∵ = 0.19,∴ x=380.
(2)初三年级人数为y+z=2000-(373+377+380+370)=500,现用分层随机抽样的方法在全校抽
取48名学生,应在初三年级抽取的人数为×500=12.
(3)初一年级应抽取学生的人数为×750=18,初二年级应抽取学的人数为×750=18,
∴该校所有学生体重的平均数约为=×40+×50+×60=48.75(kg)
17.解:(1)因为a<b,所以不等式(x-a)(x-b)<0的解集为{x|a<x<b),由已知,得a=-1,b=2.
(2)因为fx)=2x-3,由f(x0)=0,得2x0=3,所以x=,f(2x0)=22x0-3=(2x0)2-3=32-3=6.
18.解:(1)证明:∵点E,F分别是AC,AD的中点,∴EF∥CD,又CD 平面BCD,EF平面BCD,
∴EF∥平面BCD;
(2)∵AB⊥平面BCD,∴∠ADB即为直线AD与平面BCD所成的角,∴∠ADB=45°,∴AB=BD=4,
∵BC⊥BD,∴S BCD=·BC·BD=×3×4=6,
∴三棱维A-BCD的体积V=·S BCD·AB=×6×4=8.
19.解:(1)数)y=3sin(x-),对应五点如下表所示:
x- 0 2
x
y 0 3 0 -3 0
将坐标(,0),(,3),(,0),(,-3),(,0)分别描在平面直角坐标系中,连接各点如下图所示:
(2)方法一:将y=sinx的横坐标扩大为原来的2倍,可得y=sinx,再将函数图象向右平移个单位可得y=sin(x-),最后将纵坐标伸长为原来的3倍,即可得y=3sin(x-);
方法二:将y=sinx向右平移个单位可得y=sim(x-),再将横坐标扩大为原来的2倍,可得
y=sin(x-),最后将纵坐标伸长为原来的3倍,即可得y=3sin(x-);
(3)由正弦函数的图象与性质可知,函数y=3sin(x-)的对称轴满足x-=+k,k∈Zk∈Z,解得x=+2k,k∈Z;由正弦函数的图象与性质可知,函数y=3sin(x-)的对称中心满足x-=k,k∈Z,解得x=+2k,所以对称中心为(+2k,0),k∈Z;
由正弦函数的图象与性质可知,函数y=3sin(x-)的单调递增区间满足x-∈[-+2k+2k],k∈Z,解得x∈[-+4k+4k],k∈Z,所以单调递增区间为[-+4k+4k],k∈Z.
数学模拟试卷(六)
本试卷包括选择题、填空题、和解答题三部分。时量90分钟,满分100分
选择题:本大题共10个小题,每小题4分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1、如图所示的几何体是
A、五棱锥
B、五棱台
C、五棱柱
D、五面体
2、某中学有高中生480人,初中生240人,为了了解学生的身体状况,采用分层抽样的方法,从该校学生中抽取容量为n的样本,其中高中生有12人,那么n等于
A、6 B、9 C、12 D、18
3、与-30终边相同的角是
-330 B、30 C、150 D、330
已知f(x)奇函数,其部分图象如下左图所示,则f(x)的图象是
A B
C D
5、把函数y=sinx的图像向左平移 个单位后所得的新函数是
A、y=-cosx B、y=sinx- C、y=sinx+ D、y=cosx
6、已知命题p: xR,ax2+2x+30,若命题p为假命题,则实数a的取值范围是
A、{a|a} B、{a|a≤} C、{a|a≤} D、{a|a≥}
函数f(x)=,若f(a)=1,则a=
A、0 B、1 C、 D、3
8、已知A+B=45,则(1+)(1+)的值为
A、2 B、1 C、 D、不确定
9、已知扇形的圆心角为2,周长为8,则扇形的面积为
A、 B、4 C、8 D、
10、若函数f(x)是定义在R上的偶函数,在[0,+∞)上是减函数,且f(2)=0,则不等式f()0的解集是
A、( ,4) B、(0,)∪(4,+∞) C、(,2) D、(0,)∪(2,+∞)
填空题:本大题共5小题,每小题4分,满分20分。
已知集合A={1,2,a},B={1,3},若B A,则a=
采用简单随机抽样的方法,从含有5个个体的总体中抽取一个容量为2的样本,某个个体被抽到的概率为
数据3.2,3.6,4.5,2.4,4.6,6.4,7.8,7.9,8.0,8.1,8.4,8.6的75%分位数是
在长方体ABCD-A1B1C1D1中,与棱AA1垂直且异面的棱的条数是
如图所示,一学生在河岸紧靠河边笔直行走,在A处时,
经观察,在河对岸有一参照物C与学生前进方向成30°角,
学生前进200m后,测得该参照物与前进方向成75°角,则
河的宽度为 m.
解答题:本大题共4个小题,满分40分,解答应写出文字说明、证明过程或演算步骤 。
(本小题满分10分)
某初级中学共有学生2000名,各年级男、女生人数如下表:
年级 初一年级 初二年级 初三年级
女生 373 x y
男生 377 370 z
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求x的值;
(2)现用分层随机抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(3)在(2)中,若所抽取的初一年级、初二年级、初三年级三个年级学生的体重的平均数分别是40kg,50kg,60kg,估计该校所有学生体重的平均数.
(本小题满分10分)
已知不等式(x-a)(x-b) 0(其中ab)的解集为{x|-1x 2},函数f(x)=bx+a-2.
求a,b的值;
若函数f(x)的零点为x0,求x0和f(2x0)的值.
18、(本小题满分10分)
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,BC=3,BD=4,直线AD与平面BCD所成的角为45,点E,F分别是AC,AD的中点.
(1)求证:EF∥平面BCD;
(2)求三棱锥A-BCD的体积.
19、(本小题满分10分)
已知函数y=3sin(x-).
用“五点法”作函数的图象;
说出此图象是由y=sinx的图象经过怎样的变换得到的;
求此函数的对称轴、对称中心、单调递增区间。
参考答案
一、选择题
1-5 C D D B D 6-10 C B A B A
二、填空题
11. 3 12. 13.8.05 14.4 15.50( +1)
三、解答题
16.解:(1)∵ = 0.19,∴ x=380.
(2)初三年级人数为y+z=2000-(373+377+380+370)=500,现用分层随机抽样的方法在全校抽
取48名学生,应在初三年级抽取的人数为×500=12.
(3)初一年级应抽取学生的人数为×750=18,初二年级应抽取学的人数为×750=18,
∴该校所有学生体重的平均数约为=×40+×50+×60=48.75(kg)
17.解:(1)因为a<b,所以不等式(x-a)(x-b)<0的解集为{x|a<x<b),由已知,得a=-1,b=2.
(2)因为fx)=2x-3,由f(x0)=0,得2x0=3,所以x=,f(2x0)=22x0-3=(2x0)2-3=32-3=6.
18.解:(1)证明:∵点E,F分别是AC,AD的中点,∴EF∥CD,又CD 平面BCD,EF平面BCD,
∴EF∥平面BCD;
(2)∵AB⊥平面BCD,∴∠ADB即为直线AD与平面BCD所成的角,∴∠ADB=45°,∴AB=BD=4,
∵BC⊥BD,∴S BCD=·BC·BD=×3×4=6,
∴三棱维A-BCD的体积V=·S BCD·AB=×6×4=8.
19.解:(1)数)y=3sin(x-),对应五点如下表所示:
x- 0 2
x
y 0 3 0 -3 0
将坐标(,0),(,3),(,0),(,-3),(,0)分别描在平面直角坐标系中,连接各点如下图所示:
(2)方法一:将y=sinx的横坐标扩大为原来的2倍,可得y=sinx,再将函数图象向右平移个单位可得y=sin(x-),最后将纵坐标伸长为原来的3倍,即可得y=3sin(x-);
方法二:将y=sinx向右平移个单位可得y=sim(x-),再将横坐标扩大为原来的2倍,可得
y=sin(x-),最后将纵坐标伸长为原来的3倍,即可得y=3sin(x-);
(3)由正弦函数的图象与性质可知,函数y=3sin(x-)的对称轴满足x-=+k,k∈Zk∈Z,解得x=+2k,k∈Z;由正弦函数的图象与性质可知,函数y=3sin(x-)的对称中心满足x-=k,k∈Z,解得x=+2k,所以对称中心为(+2k,0),k∈Z;
由正弦函数的图象与性质可知,函数y=3sin(x-)的单调递增区间满足x-∈[-+2k+2k],k∈Z,解得x∈[-+4k+4k],k∈Z,所以单调递增区间为[-+4k+4k],k∈Z.
同课章节目录
