青岛版五下数学 智慧广场 简单的组合 课件(12张PPT)
文档属性
| 名称 | 青岛版五下数学 智慧广场 简单的组合 课件(12张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 984.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-13 20:16:31 | ||
图片预览




文档简介
(共12张PPT)
智慧广场
——简单的组合问题
青岛版数学五年级下册
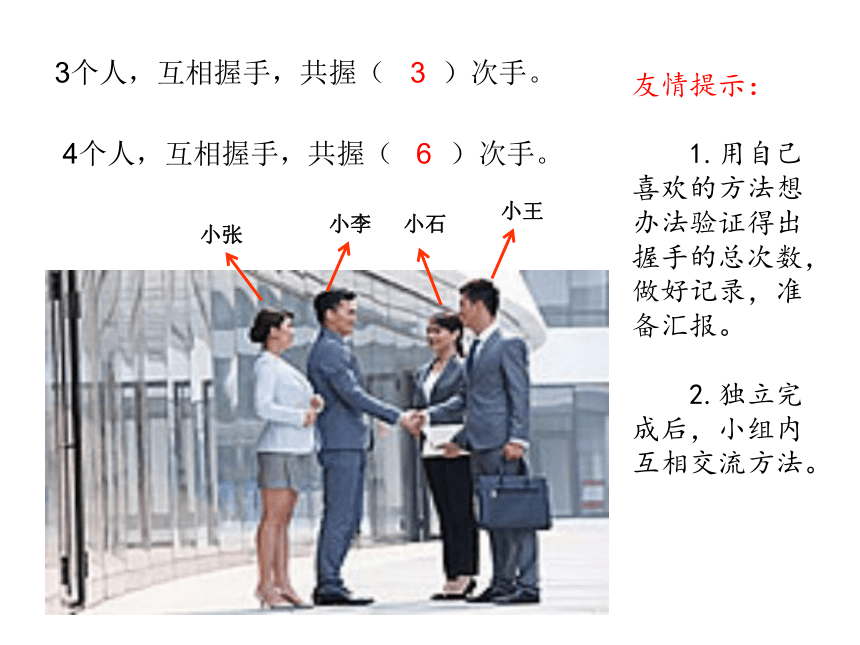
3个人,互相握手,共握( )次手。
3
3个人,互相握手,共握( )次手。
4个人,互相握手,共握( )次手。
小张
小李
小王
小石
3
6
友情提示:
1.用自己喜欢的方法想办法验证得出握手的总次数,做好记录,准备汇报。
2.独立完成后,小组内互相交流方法。
﹒
﹒
﹒
﹒
﹒
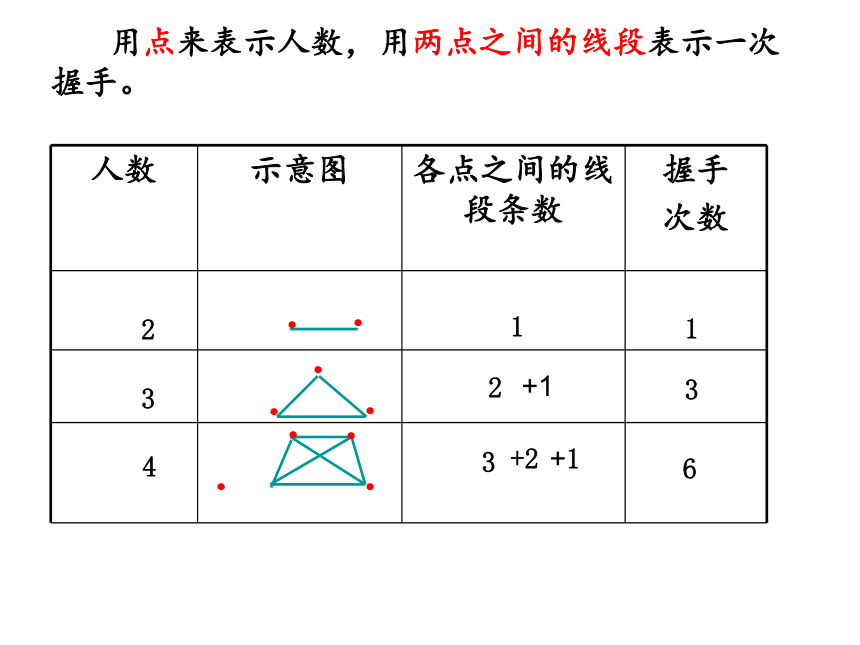
人数 示意图 各点之间的线段条数 握手
次数
2
1
1
3
3
4
3
6
2
用点来表示人数,用两点之间的线段表示一次握手。
﹒
﹒
﹒
﹒
+1
+2
+1
3个人,互相握手,共握( 3 )次手。
4个人,互相握手,共握( 6 )次手。
2+1=3
3+2+1=6
5人互相握手,一共握( )次。
10
如果6人呢?
10人呢?
100人呢?
......
你有什么发现?
3个人,互相握手,共握( 3 )次手。
4个人,互相握手,共握( 6 )次手。
2+1=3
3+2+1=6
5人互相握手,一共握( )次。
10
如果6人呢?
10人呢?
100人呢?
......
如果人数用字母n来表示,那么握手的次数就用1+2+3+4......+(n-1)来计算。
生活中的组合问题
1.四一班举行象棋比赛,共有5名选手,每两名选手比一场,共有几场比赛?
3.
有2、3、4、5四个数字,从中选取两个数字组成两位数,能组成几个两位数?
生活中的组合问题
23,24,25
32,34,35
42,43,45
52,53,54
4 × 3 = 12(个)
有几个数字
每个数字在十位能组几个两位数
可以重复选择!
顺序不同,就产生不同的组合方式!
一辆从北京到上海的特快列车,中途要停5个站,铁路部门要为这趟列车准备多少种不同的车票呢?
生活中的组合问题
这节课经历了怎样的学习过程?
简单的
组合问题
列举法
画图法
计算法
有次序;
不遗漏,不重复
加法
乘法
可以重复选择
不可以重复选择
线段连点
智慧广场
——简单的组合问题
青岛版数学五年级下册
3个人,互相握手,共握( )次手。
3
3个人,互相握手,共握( )次手。
4个人,互相握手,共握( )次手。
小张
小李
小王
小石
3
6
友情提示:
1.用自己喜欢的方法想办法验证得出握手的总次数,做好记录,准备汇报。
2.独立完成后,小组内互相交流方法。
﹒
﹒
﹒
﹒
﹒
人数 示意图 各点之间的线段条数 握手
次数
2
1
1
3
3
4
3
6
2
用点来表示人数,用两点之间的线段表示一次握手。
﹒
﹒
﹒
﹒
+1
+2
+1
3个人,互相握手,共握( 3 )次手。
4个人,互相握手,共握( 6 )次手。
2+1=3
3+2+1=6
5人互相握手,一共握( )次。
10
如果6人呢?
10人呢?
100人呢?
......
你有什么发现?
3个人,互相握手,共握( 3 )次手。
4个人,互相握手,共握( 6 )次手。
2+1=3
3+2+1=6
5人互相握手,一共握( )次。
10
如果6人呢?
10人呢?
100人呢?
......
如果人数用字母n来表示,那么握手的次数就用1+2+3+4......+(n-1)来计算。
生活中的组合问题
1.四一班举行象棋比赛,共有5名选手,每两名选手比一场,共有几场比赛?
3.
有2、3、4、5四个数字,从中选取两个数字组成两位数,能组成几个两位数?
生活中的组合问题
23,24,25
32,34,35
42,43,45
52,53,54
4 × 3 = 12(个)
有几个数字
每个数字在十位能组几个两位数
可以重复选择!
顺序不同,就产生不同的组合方式!
一辆从北京到上海的特快列车,中途要停5个站,铁路部门要为这趟列车准备多少种不同的车票呢?
生活中的组合问题
这节课经历了怎样的学习过程?
简单的
组合问题
列举法
画图法
计算法
有次序;
不遗漏,不重复
加法
乘法
可以重复选择
不可以重复选择
线段连点
