苏教版六下数学 6.3反比例的意义 课件(共20张PPT)
文档属性
| 名称 | 苏教版六下数学 6.3反比例的意义 课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1023.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-13 18:23:36 | ||
图片预览







文档简介
(共20张PPT)
反比例的意义
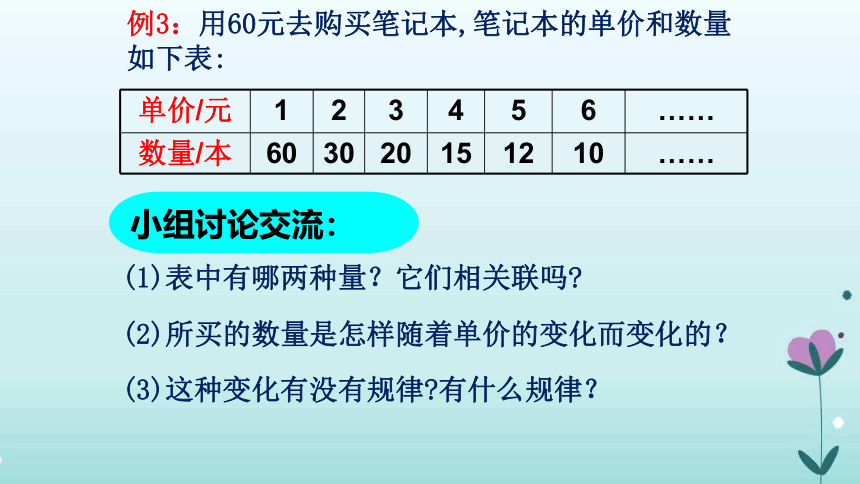
(1)表中有哪两种量?它们相关联吗
(2)所买的数量是怎样随着单价的变化而变化的?
(3)这种变化有没有规律 有什么规律?
单价/元 1 2 3 4 5 6 ……
数量/本 60 30 20 15 12 10 ……
例3:用60元去购买笔记本,笔记本的单价和数量如下表:
小组讨论交流:
(1)表中有哪两种量?它们相关联吗
单价/元 1 2 3 4 5 6 …
数量/本 60 30 20 15 12 10 …
例3:用60元去购买笔记本,笔记本的单价和数量如下表:
小组讨论交流:
单价和数量是两种相关联的量。
单价/元 1 2 3 4 5 6 …
数量/本 60 30 20 15 12 10 …
例3:用60元去购买笔记本,笔记本的单价和数量如下表:
小组讨论交流:
(2)所买的数量是怎样随着单价的变化而变化的?
单价越高,购买的本数越少。
单价越低,购买的本数越多。
单价越高,购买的本数越少。
单价越低,购买的本数越多。
单价/元 1 2 3 4 5 6 …
数量/本 60 30 20 15 12 10 …
例3:用60元去购买笔记本,笔记本的单价和数量如下表:
小组讨论交流:
(3)这种变化有没有规律 有什么规律?
单价和数量的积( )总是一定的。
总价
单价和数量是两种相关联的量,
单价变化,数量也随着变化。
单价和数量的积(总价)总是一定。
单价和数量成反比例关系。
这两个量是成反比例的量。
单价×数量=总价(一定)
(1)填表,并说说工作时间是随着哪个量的变化而变化的。
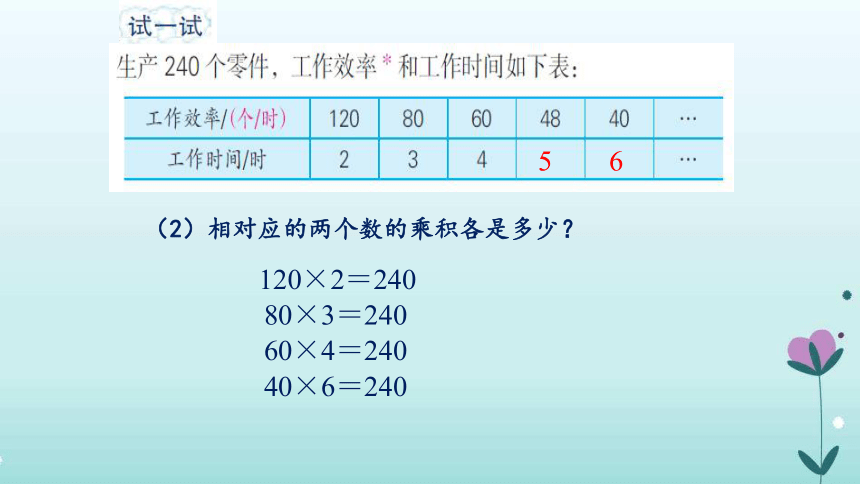
(2)相对应的两个数的乘积各是多少?
(3)这个乘积表示的实际意义是什么?你能用式子表示它与工作时间和工作效率之间的关系吗?
(4)工作时间与工作效率成反比例吗?为什么?
工作时间随着工作效率的变化而变化。
(1)填表,并说说工作时间是随着哪个量的变化而变化的。
5
6
5
6
(2)相对应的两个数的乘积各是多少?
120×2=240
80×3=240
60×4=240
40×6=240
5
6
(3)这个乘积表示的实际意义是什么?你能用式子表示它与工作时间和工作效率之间的关系吗?
120×2=240
80×3=240
60×4=240
40×6=240
乘积表示工作总量。
工作效率×工作时间=工作总量
240
240
240
240
5
6
(4)工作时间与工作效率成反比例吗?为什么?
工作时间与工作效率成反比例。
因为:工作效率×工作时间=工作总量
(一定)
比较两表,看看它们有什么共同点?
1.它们都是两种相关联的量;都是一种量变化另一种量也随着变化;
2.两个相对应的数的乘积相同。
乘积
单价/元 1 2 3 4 5 6 …
数量/本 60 30 20 15 12 10 …
5
6
你能举例说说,生活中还有哪些成反比例的量?
找一找:
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用式子表示:
y
x
=k
(一定)
×
(1)120名同学参加团体操表演,每排的人数和排数。( )
成反比例
(3)一个人的年龄和体重。( )
1.判断下面每题中的两种量是否成反比例,并说明理由。
(5)一个商场每天的营业时间一定, 每天接待顾客的数量与营业额。( )
不成反比例
(4)甲数和乙数互为倒数,甲数和乙数。( )
(2)长方形的面积一定,长方形的长与宽。( )
成反比例
判一判:
(6)行驶的速度一定,行驶的路程和时间。( )
成反比例
不成反比例
不成反比例
正比例 反比例
相同点
不同点
都是两种相关联的量,一种量随着另一种量变化。
1.变化的方向相同,一种量扩大或缩小,另一种量也扩大或缩小。
1.变化的方向相反,一种量扩大或缩小,另一种量反而缩小或扩大。
2.相对应的每两个数的比值是一定的。
2.相对应的每两个数的乘积是一定的。
3.关系式:
x × y = k(一定)
4.图像上的点在一条直线上。
4.图像上的点在一条曲线上。
大
定
字
图
比一比
成反比例
成正比例
不成比例
成正比例
底面积×高=45
质量÷体积=7.8
周长÷直径=π
2.
①路程、时间、速度
②单价、数量、总价
③全班人数、女生人数、男生人数
④圆的面积、圆周率、圆的半径
用一用:
就密信中的数量进行运用,看看有没有比例关系存在?
你有哪些收获?
反比例的意义
(1)表中有哪两种量?它们相关联吗
(2)所买的数量是怎样随着单价的变化而变化的?
(3)这种变化有没有规律 有什么规律?
单价/元 1 2 3 4 5 6 ……
数量/本 60 30 20 15 12 10 ……
例3:用60元去购买笔记本,笔记本的单价和数量如下表:
小组讨论交流:
(1)表中有哪两种量?它们相关联吗
单价/元 1 2 3 4 5 6 …
数量/本 60 30 20 15 12 10 …
例3:用60元去购买笔记本,笔记本的单价和数量如下表:
小组讨论交流:
单价和数量是两种相关联的量。
单价/元 1 2 3 4 5 6 …
数量/本 60 30 20 15 12 10 …
例3:用60元去购买笔记本,笔记本的单价和数量如下表:
小组讨论交流:
(2)所买的数量是怎样随着单价的变化而变化的?
单价越高,购买的本数越少。
单价越低,购买的本数越多。
单价越高,购买的本数越少。
单价越低,购买的本数越多。
单价/元 1 2 3 4 5 6 …
数量/本 60 30 20 15 12 10 …
例3:用60元去购买笔记本,笔记本的单价和数量如下表:
小组讨论交流:
(3)这种变化有没有规律 有什么规律?
单价和数量的积( )总是一定的。
总价
单价和数量是两种相关联的量,
单价变化,数量也随着变化。
单价和数量的积(总价)总是一定。
单价和数量成反比例关系。
这两个量是成反比例的量。
单价×数量=总价(一定)
(1)填表,并说说工作时间是随着哪个量的变化而变化的。
(2)相对应的两个数的乘积各是多少?
(3)这个乘积表示的实际意义是什么?你能用式子表示它与工作时间和工作效率之间的关系吗?
(4)工作时间与工作效率成反比例吗?为什么?
工作时间随着工作效率的变化而变化。
(1)填表,并说说工作时间是随着哪个量的变化而变化的。
5
6
5
6
(2)相对应的两个数的乘积各是多少?
120×2=240
80×3=240
60×4=240
40×6=240
5
6
(3)这个乘积表示的实际意义是什么?你能用式子表示它与工作时间和工作效率之间的关系吗?
120×2=240
80×3=240
60×4=240
40×6=240
乘积表示工作总量。
工作效率×工作时间=工作总量
240
240
240
240
5
6
(4)工作时间与工作效率成反比例吗?为什么?
工作时间与工作效率成反比例。
因为:工作效率×工作时间=工作总量
(一定)
比较两表,看看它们有什么共同点?
1.它们都是两种相关联的量;都是一种量变化另一种量也随着变化;
2.两个相对应的数的乘积相同。
乘积
单价/元 1 2 3 4 5 6 …
数量/本 60 30 20 15 12 10 …
5
6
你能举例说说,生活中还有哪些成反比例的量?
找一找:
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用式子表示:
y
x
=k
(一定)
×
(1)120名同学参加团体操表演,每排的人数和排数。( )
成反比例
(3)一个人的年龄和体重。( )
1.判断下面每题中的两种量是否成反比例,并说明理由。
(5)一个商场每天的营业时间一定, 每天接待顾客的数量与营业额。( )
不成反比例
(4)甲数和乙数互为倒数,甲数和乙数。( )
(2)长方形的面积一定,长方形的长与宽。( )
成反比例
判一判:
(6)行驶的速度一定,行驶的路程和时间。( )
成反比例
不成反比例
不成反比例
正比例 反比例
相同点
不同点
都是两种相关联的量,一种量随着另一种量变化。
1.变化的方向相同,一种量扩大或缩小,另一种量也扩大或缩小。
1.变化的方向相反,一种量扩大或缩小,另一种量反而缩小或扩大。
2.相对应的每两个数的比值是一定的。
2.相对应的每两个数的乘积是一定的。
3.关系式:
x × y = k(一定)
4.图像上的点在一条直线上。
4.图像上的点在一条曲线上。
大
定
字
图
比一比
成反比例
成正比例
不成比例
成正比例
底面积×高=45
质量÷体积=7.8
周长÷直径=π
2.
①路程、时间、速度
②单价、数量、总价
③全班人数、女生人数、男生人数
④圆的面积、圆周率、圆的半径
用一用:
就密信中的数量进行运用,看看有没有比例关系存在?
你有哪些收获?
