苏教版六下数学 6.4正比例和反比例练习 课件(共33张PPT)
文档属性
| 名称 | 苏教版六下数学 6.4正比例和反比例练习 课件(共33张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 763.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-13 20:30:34 | ||
图片预览











文档简介
(共33张PPT)
苏教版小学数学第十二册
正反比例对比练习
(1)什么叫做成正比例的量
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
(2)什么叫做成反比例的量
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们之间的关系叫做反比例关系。
正、反比例的相同点和不同点
正比例 反比例
相同点
不同点
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们之间的关系叫做反比例关系。
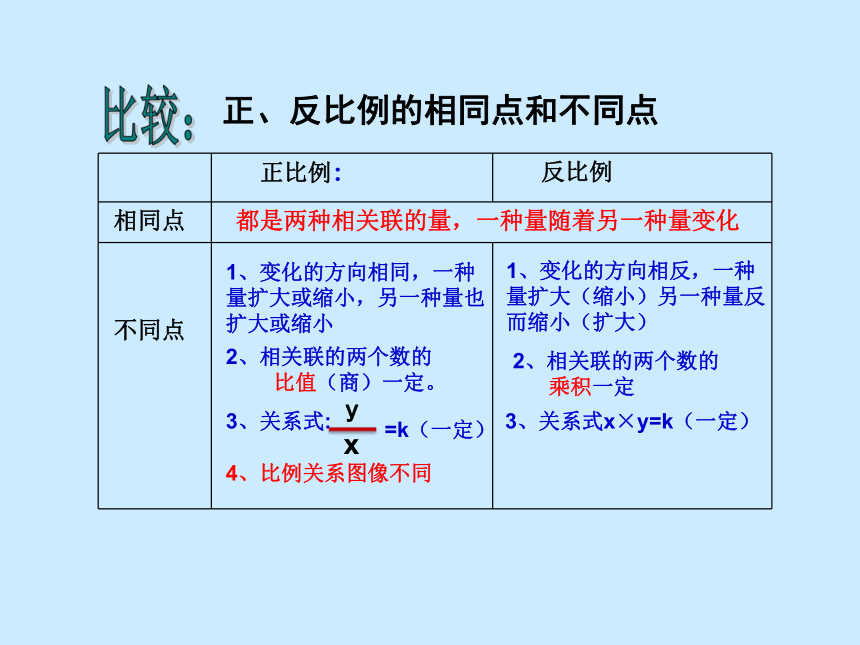
正、反比例的相同点和不同点
正比例: 反比例
相同点
不同点
1、变化的方向相同,一种量扩大或缩小,另一种量也扩大或缩小
都是两种相关联的量,一种量随着另一种量变化
1、变化的方向相反,一种量扩大(缩小)另一种量反而缩小(扩大)
2、相关联的两个数的
比值(商)一定。
2、相关联的两个数的
乘积一定
3、关系式:
3、关系式x×y=k(一定)
y
x
=k(一定)
4、比例关系图像不同
思考:
要判断两种量是否成正比例主要看什么?
判断两种量是否成反比例呢?
比值(商)是否一定
乘积是否一定
正、反比例的判断方法
(1)分析数量关系,确定哪两种量是相关联的量。
(2)分析这两种相关联的量,它们之间的关系式商一定,还是积一定。
(3)如果商一定,就成正比例,如果积一定,就成反比例。
一、选择(把正确答案的序号填在括号里)
(1)成正比例的两种量在变化过程中,一种量缩小,另一种量就( )。
A.扩大 B.缩小 C.不变化
(2)成正比例的两种量在变化时的规律是它们的( )不变。
A.和 B.差 C.积 D.商
(3)正方形的周长和它的边长( )。
A.成正比例 B.不成正比例
B
D
A
基础检测
(4)一堆煤,已烧的吨数和剩下的吨数( )。
A.成正比例 B.不成正比例
(5)成反比例的两种量中,一种量扩大,另一种量( )。
A.随着扩大 B.随着缩小 C.不变
(6)成反比例的两种量变化的规律是它们的( )一定。
A.和 B.差 C.积 D.商
B
B
C
(7)一本书的总字数一定,每页字数与页数( )。
A.成反比例 B.不成反比例
(8)三角形的面积一定,它的底和高( )。
A.成反比例 B.不成反比例
A
A
二、判断下面各题中的两种量是否成比例,成什么比例.
1、练习本的单价一定,买练习本的数量和总价.
2、化肥总重量一定,用去的数量和剩下的数量.
3、总人数一定,每行的人数和行数.
成正比例
不成比例
成反比例
同学们:我们已经学过哪些数量关系?它们之间成比例关系吗?成什么比例关系?
1、在单价、数量和总价中,
一定,( )和( )成( )比例。
一定,( )和( )成( )比例。
一定,( )和( )成( )比例。
总价
单价
数量
反
单价
数量
总价
正
数量
单价
总价
正
2、在速度、时间和路程中,
当速度一定,路程和时间( )比例
当路程一定,速度和时间( )比例
当时间一定,路程和速度( )比例
成正
成反
成正
3、工作效率、工作时间和工作总量,
当工作效率一定,工作总量和工作时间
成( )比例
当工作时间一定,工作效率和工作总量
成( )比例
当工作总量一定,工作效率和工作时间
成( )比例
正
正
反
4、每公顷产量、总产量和公顷数
每公顷产量一定,总产量和公顷数( )比例
公顷数一定,每公顷产量和总产量( )比例
总产量一定,每公顷产量和公顷数( )比例
成正
成正
成反
5、在乘法中,
积一定,两个因数( )比例
一个因数一定,另一个因数和积( )比例
成反
成正
6、在减法中,
差一定,减数和被减数( )比例
减数一定,被减数和差( )比例
被减数一定,减数和差( )比例
不成
不成
不成
7、在没有余数的除法中,
商一定,除数和被除数( )比例
除数一定,商和被除数( )比例
被除数一定,除数和商( )比例
成正
成正
成反
8、在比中,
前项一定,比的后项和比值( )比例
比值一定,比的前项和后项( )比例
后项一定,比的前项和比值( )比例
成反
成正
成正
9、在长方形中,
长一定,面积和宽( )比例
宽一定,面积和长( )比例
面积一定,长和宽( )比例
周长一定,长和宽( )比例
成正
成正
成反
不成
10、在平行四边形里,
底一定,面积和高( )比例
高一定,面积和底( )比例
面积一定,底和高( )比例
成正
成正
成反
11、在圆中,
面积和半径( )比例
周长和半径( )比例
直径和半径( )比例
直径和面积( )比例
不成
成正
成正
不成
12、在比例尺中,
比例尺一定,图上距离和实际距离( )比例
图上距离一定,比例尺和实际距离( )比例
实际距离一定,比例尺和图上距离( )比例
成正
成反
成正
13、在长方体中,
底面积一定,体积和高( )比例
体积一定,底面积和高( )比例
高一定,底面积和体积( )比例
我们学过的数量关系非常多,再例如圆柱和圆锥里的,有待大家去思考!
成正
成反
成正
三、先判断a和b成什么比例,再填空.
(1)a和b成( )比例。
a 6 3 1.5
b 4 0.5 3 2
a 12 30 6 5
b 10 4 15
(2)a和b成( )比例
正
0.75
4.5
1
反
20
8
24
一、填空
1、y=8x,y和x成( )比例。
2、已知a÷b=c,当a一定时,b和c( )。当b一定时,a与c( )。
3、 7﹕ x = y﹕15,x 和 y成( )比例。
4、 甲数和乙数互为倒数,甲数和乙数成( )比例。
5、 3×4=12(一定), 3和4( )比例。
正
成正比例
成反比例
反
反
不成
二、仔细甄选(把正确答案的序号填在括号内)
1、X ×Y=21 ( )
A .X和Y成反比例 B. X 和Y成正比例 C. X和 Y 不成比例。
2、面粉的质量一定,出粉率和小麦的质量( )
A 成正比例 B 成反比例 C 不成比例
A
B
3、在一定的路程内,车轮的周长和转动的圈数( )
A 成正比例 B 成反比例 C 不成比例
4、圆的周长一定,它的直径和圆周率( )
A 成正比例 B 成反比例 C 不成比例
B
C
三、判断下面x、y两种量是否成比例,成什么比例。
1、x+y=3
2、x=3y
3、
4、
5、xy=k+2(k一定)
不成比例
成正比例
成正比例
成反比例
成反比例
6、xy+12=36
成反比例
拓展拔尖:看谁最聪明
讨论1:给我们的教室铺地板砖,方砖的面积和所需块数是不是成反比例?
分析:
1.方砖的面积和所需块数是两种相关联的量。
2.方砖的面积大,所需块数少;方砖的面积小,所需块数多。
3.方砖的面积×所需块数=教室地的面积。(地面面积是固定不变的)
具备了成反比例关系的条件,所以在教室地面面积一定的条件下,方砖的面积和所需块数成反比例。
讨论2
铺地面积一定时,方砖边长与所需块数成不成
比例?为什么?
因为
方砖边长
2
×所需块数=铺地面积
所以
方砖边长与所需块数不成反比例.
方砖边长的平方与所需块数成反比例.
苏教版小学数学第十二册
正反比例对比练习
(1)什么叫做成正比例的量
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
(2)什么叫做成反比例的量
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们之间的关系叫做反比例关系。
正、反比例的相同点和不同点
正比例 反比例
相同点
不同点
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系。
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,它们之间的关系叫做反比例关系。
正、反比例的相同点和不同点
正比例: 反比例
相同点
不同点
1、变化的方向相同,一种量扩大或缩小,另一种量也扩大或缩小
都是两种相关联的量,一种量随着另一种量变化
1、变化的方向相反,一种量扩大(缩小)另一种量反而缩小(扩大)
2、相关联的两个数的
比值(商)一定。
2、相关联的两个数的
乘积一定
3、关系式:
3、关系式x×y=k(一定)
y
x
=k(一定)
4、比例关系图像不同
思考:
要判断两种量是否成正比例主要看什么?
判断两种量是否成反比例呢?
比值(商)是否一定
乘积是否一定
正、反比例的判断方法
(1)分析数量关系,确定哪两种量是相关联的量。
(2)分析这两种相关联的量,它们之间的关系式商一定,还是积一定。
(3)如果商一定,就成正比例,如果积一定,就成反比例。
一、选择(把正确答案的序号填在括号里)
(1)成正比例的两种量在变化过程中,一种量缩小,另一种量就( )。
A.扩大 B.缩小 C.不变化
(2)成正比例的两种量在变化时的规律是它们的( )不变。
A.和 B.差 C.积 D.商
(3)正方形的周长和它的边长( )。
A.成正比例 B.不成正比例
B
D
A
基础检测
(4)一堆煤,已烧的吨数和剩下的吨数( )。
A.成正比例 B.不成正比例
(5)成反比例的两种量中,一种量扩大,另一种量( )。
A.随着扩大 B.随着缩小 C.不变
(6)成反比例的两种量变化的规律是它们的( )一定。
A.和 B.差 C.积 D.商
B
B
C
(7)一本书的总字数一定,每页字数与页数( )。
A.成反比例 B.不成反比例
(8)三角形的面积一定,它的底和高( )。
A.成反比例 B.不成反比例
A
A
二、判断下面各题中的两种量是否成比例,成什么比例.
1、练习本的单价一定,买练习本的数量和总价.
2、化肥总重量一定,用去的数量和剩下的数量.
3、总人数一定,每行的人数和行数.
成正比例
不成比例
成反比例
同学们:我们已经学过哪些数量关系?它们之间成比例关系吗?成什么比例关系?
1、在单价、数量和总价中,
一定,( )和( )成( )比例。
一定,( )和( )成( )比例。
一定,( )和( )成( )比例。
总价
单价
数量
反
单价
数量
总价
正
数量
单价
总价
正
2、在速度、时间和路程中,
当速度一定,路程和时间( )比例
当路程一定,速度和时间( )比例
当时间一定,路程和速度( )比例
成正
成反
成正
3、工作效率、工作时间和工作总量,
当工作效率一定,工作总量和工作时间
成( )比例
当工作时间一定,工作效率和工作总量
成( )比例
当工作总量一定,工作效率和工作时间
成( )比例
正
正
反
4、每公顷产量、总产量和公顷数
每公顷产量一定,总产量和公顷数( )比例
公顷数一定,每公顷产量和总产量( )比例
总产量一定,每公顷产量和公顷数( )比例
成正
成正
成反
5、在乘法中,
积一定,两个因数( )比例
一个因数一定,另一个因数和积( )比例
成反
成正
6、在减法中,
差一定,减数和被减数( )比例
减数一定,被减数和差( )比例
被减数一定,减数和差( )比例
不成
不成
不成
7、在没有余数的除法中,
商一定,除数和被除数( )比例
除数一定,商和被除数( )比例
被除数一定,除数和商( )比例
成正
成正
成反
8、在比中,
前项一定,比的后项和比值( )比例
比值一定,比的前项和后项( )比例
后项一定,比的前项和比值( )比例
成反
成正
成正
9、在长方形中,
长一定,面积和宽( )比例
宽一定,面积和长( )比例
面积一定,长和宽( )比例
周长一定,长和宽( )比例
成正
成正
成反
不成
10、在平行四边形里,
底一定,面积和高( )比例
高一定,面积和底( )比例
面积一定,底和高( )比例
成正
成正
成反
11、在圆中,
面积和半径( )比例
周长和半径( )比例
直径和半径( )比例
直径和面积( )比例
不成
成正
成正
不成
12、在比例尺中,
比例尺一定,图上距离和实际距离( )比例
图上距离一定,比例尺和实际距离( )比例
实际距离一定,比例尺和图上距离( )比例
成正
成反
成正
13、在长方体中,
底面积一定,体积和高( )比例
体积一定,底面积和高( )比例
高一定,底面积和体积( )比例
我们学过的数量关系非常多,再例如圆柱和圆锥里的,有待大家去思考!
成正
成反
成正
三、先判断a和b成什么比例,再填空.
(1)a和b成( )比例。
a 6 3 1.5
b 4 0.5 3 2
a 12 30 6 5
b 10 4 15
(2)a和b成( )比例
正
0.75
4.5
1
反
20
8
24
一、填空
1、y=8x,y和x成( )比例。
2、已知a÷b=c,当a一定时,b和c( )。当b一定时,a与c( )。
3、 7﹕ x = y﹕15,x 和 y成( )比例。
4、 甲数和乙数互为倒数,甲数和乙数成( )比例。
5、 3×4=12(一定), 3和4( )比例。
正
成正比例
成反比例
反
反
不成
二、仔细甄选(把正确答案的序号填在括号内)
1、X ×Y=21 ( )
A .X和Y成反比例 B. X 和Y成正比例 C. X和 Y 不成比例。
2、面粉的质量一定,出粉率和小麦的质量( )
A 成正比例 B 成反比例 C 不成比例
A
B
3、在一定的路程内,车轮的周长和转动的圈数( )
A 成正比例 B 成反比例 C 不成比例
4、圆的周长一定,它的直径和圆周率( )
A 成正比例 B 成反比例 C 不成比例
B
C
三、判断下面x、y两种量是否成比例,成什么比例。
1、x+y=3
2、x=3y
3、
4、
5、xy=k+2(k一定)
不成比例
成正比例
成正比例
成反比例
成反比例
6、xy+12=36
成反比例
拓展拔尖:看谁最聪明
讨论1:给我们的教室铺地板砖,方砖的面积和所需块数是不是成反比例?
分析:
1.方砖的面积和所需块数是两种相关联的量。
2.方砖的面积大,所需块数少;方砖的面积小,所需块数多。
3.方砖的面积×所需块数=教室地的面积。(地面面积是固定不变的)
具备了成反比例关系的条件,所以在教室地面面积一定的条件下,方砖的面积和所需块数成反比例。
讨论2
铺地面积一定时,方砖边长与所需块数成不成
比例?为什么?
因为
方砖边长
2
×所需块数=铺地面积
所以
方砖边长与所需块数不成反比例.
方砖边长的平方与所需块数成反比例.
