北师大版七年级数学下册2.1两条直线的位置关系(第1课时)教学设计
文档属性
| 名称 | 北师大版七年级数学下册2.1两条直线的位置关系(第1课时)教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-14 00:00:00 | ||
图片预览



文档简介
第二章 相交线与平行线
1两条直线的位置关系(第1课时)
教学内容说明:
本节课选自北师大版数学七年级下第二章《平行线和相交线》内容第一节《两条直线的位置关系》。该节内容共分两课时,本节课是第一课时,主要内容是探索两条直线的位置关系,了解对顶角、余角、补角的定义及其性质。
1、 学生起点分析
学生的知识技能基础:学生在小学已经认识了平行线、相交线、角;在七年级上册中,已经对角及其分类有了一定的认识。这些知识储备为本节课的学习奠定了良好的基础,使学生具备了掌握本节知识的基本技能。
学生活动经验基础:在前面知识的学习过程中,教师为学生提供了广阔的可供探讨和交流的空间,学生已经经历了一些动手操作,探索发现的数学活动,积累了初步的数学活动经验,具备了一定的图形认识能力和借助图形分析问题解决问题的能力;能够将直观与简单推理相结合;在合作探究的过程中,学生在以前的数学学习中学生已经经历了小组合作的学习过程,积累了大量的方法和经验,具备了一定的合作与交流能力。
2、 教学任务分析
针对七年级学生的学情,本节从学生熟悉的、感兴趣的情境出发,引导学生自主提炼归纳出同一平面内两直线的位置关系,了解补角、余角、对顶角的概念及其性质并能够进行简单的应用;通过“让学生经历观察、操作、推理、想象等探索过程” ,发展学生的空间观念及推理能力;能从实际情境中抽象出数学模型,为后续学习“空间与图形”这一数学领域而打下坚实的基础;激发学生从数学的角度认识现实,能够敏锐的发现问题、提出问题,并运用所掌握的数学知识初步解决问题;引导学生在思考、交流、表达的基础上逐步达成有关情感与态度目标. 本节内容在教材中处于非常重要的地位,起着承前启后的作用。因此,本节课的目标是:
1.知识与技能:在具体情境中了解相交线、平行线、补角、余角、对顶角的定义,知道同角或等角的余角相等、同角或等角的补角相等、对顶角相等,并能解决一些实际问题。
2.过程与方法:经历操作、观察、猜想、交流、推理等获取信息的过程,进一步发展空间观念、推理能力和有条理表达的能力。
3.情感与态度:激发学生学习数学的兴趣,认识到现实生活中蕴含着大量的数量和图形的有关问题,这些问题可以抽象成数学问题,用数学方法予以解决。
教学重难点
在具体情境中了解相交线、平行线、补角、余角、对顶角的定义,知道同角或等角的余角相等、同角或等角的补角相等、对顶角相等,并能解决一些实际问题。
三、教学过程设计
第一环节 走进生活 引入课题
活动内容一:复习回顾
1.直线的特征是什么?
2.直线的表示方法有哪些?
活动目的:通过复习直线的特征和表示方法,引入本节课的课题:同一平面内,两条直线的位置关系。
活动内容二:两条直线的位置关系
请同学们观察有关“两条直线的位置关系”的图片,提炼出数学图形,进行归纳。
结论:1.一般地,在同一平面内,两条直线的位置关系有两种: 和 .
2. 相交线的定义: 。
3. 平行线的定义:_____________________________________ 。
活动目的:数学来源于生活,通过课前开放,引导学生从身边熟悉的图形出发,体会数学与生活的联系,总结出同一平面内两条直线的基本位置关系,体会本章内容的重要性和在生活中的广泛应用,为引入新课做好准备。通过亲身经历提炼有关数学信息的过程,可以让学生在直观有趣的问题情境中学到有价值的数学。
第二环节 思考讨论 探究新知
探究活动一
问题1:如图2.1-1,直线AB、CD相交于O,∠1和∠2有什么位置关系?尝试用自己的语言描述对顶角的定义。
对顶角的特征:①有公共顶点,②两边互为反向延长线。
结论: 直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角.
问题2:请你观察图2.1-2中还有其他的角构成对顶角吗?观察每组对顶角,你发现它们有什么大小关系
结论:∠1=∠2,∠3=∠4,对顶角相等。
〖练习〗下列各图中,∠1和∠2是对顶角的是( )
活动目的:结合具体的学习内容,设计有效的数学探究活动,使学生经历数学的发生发展过程,积累数学活动经验。设置问题1和问题2的目的是通过创设生动有趣的活动情景,为学生提供了观察、推理、交流等丰富的活动素材,使学生在自主学习的过程中,学会对顶角的概念及其性质。同时进一步培养学生抽象几何图形进行建模的能力。通过一个小练习,进一步巩固了对顶角的概念及其性质。
问题3:在图2.1-2中,∠1与∠3有什么数量关系?
结论:①∠1+∠3=180°,如果两个角的和是1800,那么称这两个角互为补角。
②类似的,如图2.1-3,∠1+∠2=90°,如果两个角的和是900,那么称这两个角互为余角。
活动:插入一段微视频,通过形象的flash动画,让学生在轻松幽默的学习气氛中再次体会“互余互补”的数量关系。
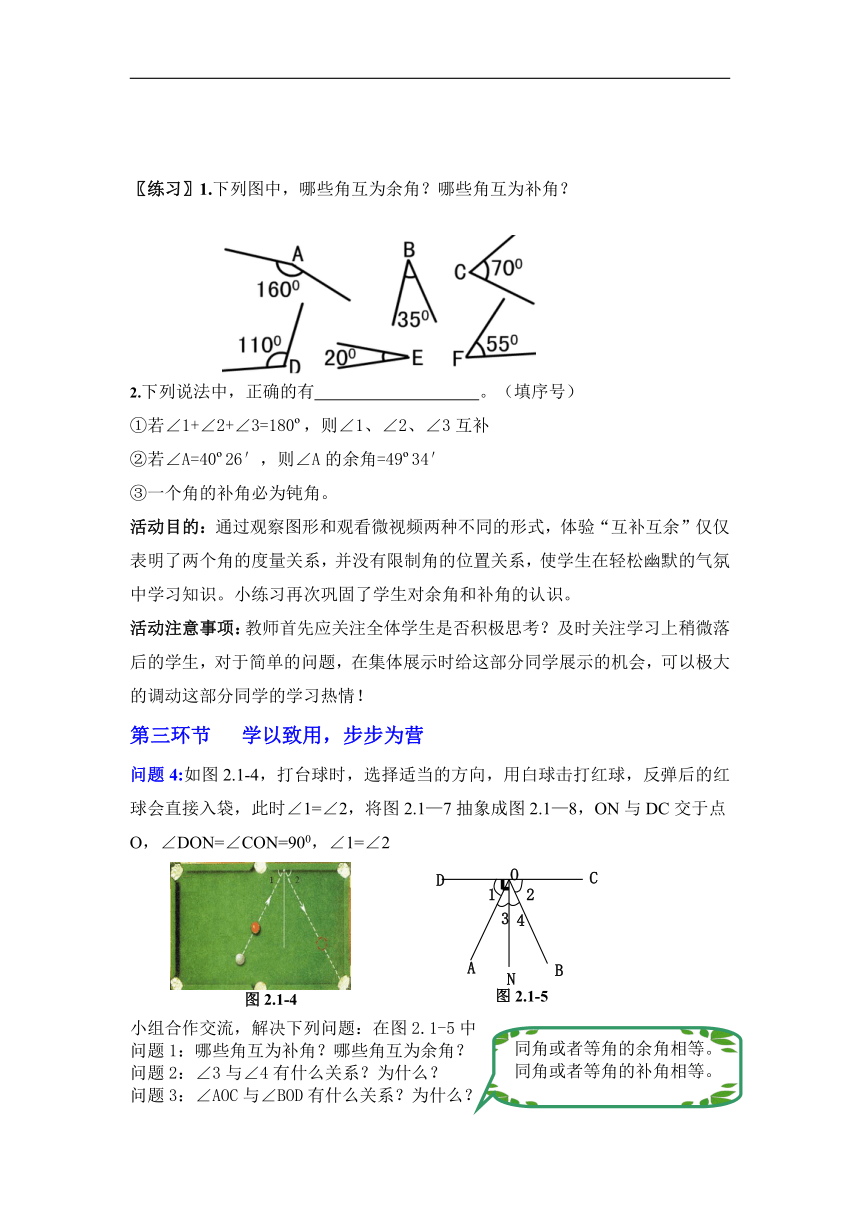
〖练习〗1.下列图中,哪些角互为余角?哪些角互为补角?
2.下列说法中,正确的有 。(填序号)
①若∠1+∠2+∠3=180 ,则∠1、∠2、∠3互补
②若∠A=40 26′,则∠A的余角=49 34′
③一个角的补角必为钝角。
活动目的:通过观察图形和观看微视频两种不同的形式,体验“互补互余”仅仅表明了两个角的度量关系,并没有限制角的位置关系,使学生在轻松幽默的气氛中学习知识。小练习再次巩固了学生对余角和补角的认识。
活动注意事项:教师首先应关注全体学生是否积极思考?及时关注学习上稍微落后的学生,对于简单的问题,在集体展示时给这部分同学展示的机会,可以极大的调动这部分同学的学习热情!
第三环节 学以致用,步步为营
问题4:如图2.1-4,打台球时,选择适当的方向,用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,将图2.1—7抽象成图2.1—8,ON与DC交于点O,∠DON=∠CON=900,∠1=∠2
小组合作交流,解决下列问题:在图2.1-5中
问题1:哪些角互为补角?哪些角互为余角?
问题2:∠3与∠4有什么关系?为什么?
问题3:∠AOC与∠BOD有什么关系?为什么?
你还能得到哪些结论?
活动目的:概括归纳得到猜想和规律,并加以验证,是学习数学的重要方法。通过生动有趣的活动情景,为学生提供了观察、推理、交流等丰富的数学活动,使学生在自主学习的过程中,掌握“同角或者等角的补角相等。”“同角或者等角的余角相等。”并能够用自己的语言说出简单推理。同时发散学生思维,让学生尽可能用多种方法来说明自己猜测的正确性,培养学生合情说理的能力。并在这个过程中,培养学生抽象几何图形进行建模的能力。本着面向全体的原则,从学生生活经验和熟悉的背景知识出发,通过创设情境串---问题串,极大的调动全体学生的参与意识,充分挖掘他们的潜能,给学生一个充分思考的机会,鼓励学生积极发言!
活动注意事项: 学生应有足够的时间和空间经历观察、猜测、推理、验证等活动过程。本环节的三个问题是环环紧扣、层层递进提出来的,前一个问题为下一个问题作好铺垫。在学习的过程中,时刻不能忘记学生是主体,一切教学活动都应当从学生已有的认知角度出发,问题环节设计跨越性不能太强,让学生在不断的探索过程中得到不同程度的感悟,自己能够主动地去探究问题的实质,体验成功的喜悦;教师要充分发散学生的思维,鼓励学生各抒己见,敢于质疑;上课要渗透合情说理的方法,进一步培养学生的推理能力。
第四环节 拓展延伸,综合应用
〖练习〗
1. ① 因为∠1+∠2=90 ,∠2+∠3=90 ,所以∠1= ,
理由是 .
② 因为∠1+∠2=180 ,∠2+∠3=180 ,所以∠1= , 理由是 .
2. 如图2.1-6已知:直线AB与CD交于点O,∠COE=900,回答下列问题:
(1)∠AOE的余角是_ ________;补角是_________。
(2)∠AOD的余角是________;补角是________;
对顶角是________。
3.如图2.1-7,直线AB、CD相交于点O,若∠BOD=42°,OA平分∠COE,求∠DOE的度数.
4.若一个角的补角等于它的余角的4倍,求这个角的度数.
5.如图2.1-8,已知直线AB、CD相交于点O,∠COE=90°.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD∶∠BOC=1∶5,求∠AOE的度数.
活动目的:通过一系列的巩固练习,可以让学生对本节的知识有更深一层的理解,也能培养学生应用知识的能力。练习题量不大,旨在对学生基本知识,基本方法,基本数学思想的运用,不加重学生的学习负担。同时习题各有侧重,锻炼学生的学习能力。具体课堂活动中,可以根据课堂效果和课堂时间,有选择、有针对性的练习。
活动的注意事项:鼓励学生自己分析问题,明晰思路,能够有条理的阐述问题,解决问题。对于学生的发言要及时肯定,有问题的地方可以先让学生自己小组合作谈论,教师予以一定引导。总而言之,希望学生能自己运用学习的知识解决问题,激发学生对数学的学习兴趣与信心,对出现的错误,一定进行积极的辨析,让学生学会解决的方法。
第五环节 学有所思 反馈巩固
归纳总结:
1. 你学到了哪些知识点?
2. 你学到了哪些方法?
3. 你还有哪些困惑?
活动目的:本环节的设置使学生学会从系统的角度把握知识方法,努力使知识结构化、网络化,引导学生时刻注意新旧知识之间的联系;鼓励学生畅谈自己学习的知识和体会,激发学生对数学的学习兴趣与信心,培养学生独自梳理知识,归纳学习方法及解题方法的能力。锻炼学生组织语言及表达能力,经历与同伴分享成果的快乐过程。
活动注意事项:教师一定让学生畅谈自己的切身感受,对于知识点的整合,更要有所思考,达到对所学知识巩固的目的。鼓励其他学生进行补充纠正,教师也应进行适时的点拨和强调。
四、教学设计反思:
1.注重数学与生活的联系
数学来源于生活,反之又服务于生活。本课时我从身边熟悉的情境出发,使学生经历从现实生活中抽象出数学模型的过程,体会本节课的重要性和在生活中的广泛应用。“几何直觉是增进数学理解力的很有效的途径,而且它可以使人增加勇气,提高修养。”通过动手操作,可以加深学生对知识的理解,从中发现知识。
2. 引入微视频,将信息技术与课堂融合
在课堂中引入一段微视频,生动幽默的语言和形象的flash动画,深深吸引着同学们,让学生们在轻松愉快的气氛中学习了有关的数学概念,再加之相应的课堂小练习,提高了学生的学习效率。
3.巧设问题串 打造高效课堂
我在教材提供的教学素材的基础上,恰当地创设情境,以问题串的方式激发学生的好奇心和求知欲,通过独立思考,不断提出问题分析问题,并创造性地解决问题,通过合作交流的方式,为学生构建了开放有效的学习环境。课堂习题的设置,题目由易到难,由简到繁,争取能让每一位学生都能领略到成功的喜悦!使学生思维分层递进,揭示概念的实质,不断完善新的知识结构,同时体验了知识的形成过程和发现的快乐,继而转化为进一步探索的内驱力;鼓励学生从多角度思考问题,充分激发学生的创新能力,使学生的思维多向开花,极大的调动学生学习数学的热情!
4.注意事项。
课堂上让学生充分发表自己的见解。教师应注意捕捉有效信息,从激励学生的角度出发,给予学生一个充分展示自我的舞台,在活动中提高学生与他人合作交流的能力,激发学生的学习兴趣。针对不同的问题,应大胆放手给学生,注意培养学生抽象几何图形的能力,简单合情说理的能力,观察分析的能力,总结归纳的能力等。讨论时,应该留给学生充分的独立思考的时间,不要让一些思维活跃的学生的回答代替了其他学生的思考,掩盖了其他学生的疑问。教师应注重学生几何语言的培养,对课堂生成的问题,应予以重视,教师可以激励学生课后继续探究,将课内学习延伸到课外,开阔学生的视野。
图2.1-1
图2.1-2
图2.1-2
图2.1-3
图2.1-4
2
D
C
O
1
3
4
A
N
B
图2.1-5
同角或者等角的余角相等。
同角或者等角的补角相等。
B
A
C
D
O
E
图2.1—6
图2.1-7
图2.1-8
PAGE
1两条直线的位置关系(第1课时)
教学内容说明:
本节课选自北师大版数学七年级下第二章《平行线和相交线》内容第一节《两条直线的位置关系》。该节内容共分两课时,本节课是第一课时,主要内容是探索两条直线的位置关系,了解对顶角、余角、补角的定义及其性质。
1、 学生起点分析
学生的知识技能基础:学生在小学已经认识了平行线、相交线、角;在七年级上册中,已经对角及其分类有了一定的认识。这些知识储备为本节课的学习奠定了良好的基础,使学生具备了掌握本节知识的基本技能。
学生活动经验基础:在前面知识的学习过程中,教师为学生提供了广阔的可供探讨和交流的空间,学生已经经历了一些动手操作,探索发现的数学活动,积累了初步的数学活动经验,具备了一定的图形认识能力和借助图形分析问题解决问题的能力;能够将直观与简单推理相结合;在合作探究的过程中,学生在以前的数学学习中学生已经经历了小组合作的学习过程,积累了大量的方法和经验,具备了一定的合作与交流能力。
2、 教学任务分析
针对七年级学生的学情,本节从学生熟悉的、感兴趣的情境出发,引导学生自主提炼归纳出同一平面内两直线的位置关系,了解补角、余角、对顶角的概念及其性质并能够进行简单的应用;通过“让学生经历观察、操作、推理、想象等探索过程” ,发展学生的空间观念及推理能力;能从实际情境中抽象出数学模型,为后续学习“空间与图形”这一数学领域而打下坚实的基础;激发学生从数学的角度认识现实,能够敏锐的发现问题、提出问题,并运用所掌握的数学知识初步解决问题;引导学生在思考、交流、表达的基础上逐步达成有关情感与态度目标. 本节内容在教材中处于非常重要的地位,起着承前启后的作用。因此,本节课的目标是:
1.知识与技能:在具体情境中了解相交线、平行线、补角、余角、对顶角的定义,知道同角或等角的余角相等、同角或等角的补角相等、对顶角相等,并能解决一些实际问题。
2.过程与方法:经历操作、观察、猜想、交流、推理等获取信息的过程,进一步发展空间观念、推理能力和有条理表达的能力。
3.情感与态度:激发学生学习数学的兴趣,认识到现实生活中蕴含着大量的数量和图形的有关问题,这些问题可以抽象成数学问题,用数学方法予以解决。
教学重难点
在具体情境中了解相交线、平行线、补角、余角、对顶角的定义,知道同角或等角的余角相等、同角或等角的补角相等、对顶角相等,并能解决一些实际问题。
三、教学过程设计
第一环节 走进生活 引入课题
活动内容一:复习回顾
1.直线的特征是什么?
2.直线的表示方法有哪些?
活动目的:通过复习直线的特征和表示方法,引入本节课的课题:同一平面内,两条直线的位置关系。
活动内容二:两条直线的位置关系
请同学们观察有关“两条直线的位置关系”的图片,提炼出数学图形,进行归纳。
结论:1.一般地,在同一平面内,两条直线的位置关系有两种: 和 .
2. 相交线的定义: 。
3. 平行线的定义:_____________________________________ 。
活动目的:数学来源于生活,通过课前开放,引导学生从身边熟悉的图形出发,体会数学与生活的联系,总结出同一平面内两条直线的基本位置关系,体会本章内容的重要性和在生活中的广泛应用,为引入新课做好准备。通过亲身经历提炼有关数学信息的过程,可以让学生在直观有趣的问题情境中学到有价值的数学。
第二环节 思考讨论 探究新知
探究活动一
问题1:如图2.1-1,直线AB、CD相交于O,∠1和∠2有什么位置关系?尝试用自己的语言描述对顶角的定义。
对顶角的特征:①有公共顶点,②两边互为反向延长线。
结论: 直线AB与CD相交于点O,∠1与∠2有公共顶点O,它们的两边互为反向延长线,这样的两个角叫做对顶角.
问题2:请你观察图2.1-2中还有其他的角构成对顶角吗?观察每组对顶角,你发现它们有什么大小关系
结论:∠1=∠2,∠3=∠4,对顶角相等。
〖练习〗下列各图中,∠1和∠2是对顶角的是( )
活动目的:结合具体的学习内容,设计有效的数学探究活动,使学生经历数学的发生发展过程,积累数学活动经验。设置问题1和问题2的目的是通过创设生动有趣的活动情景,为学生提供了观察、推理、交流等丰富的活动素材,使学生在自主学习的过程中,学会对顶角的概念及其性质。同时进一步培养学生抽象几何图形进行建模的能力。通过一个小练习,进一步巩固了对顶角的概念及其性质。
问题3:在图2.1-2中,∠1与∠3有什么数量关系?
结论:①∠1+∠3=180°,如果两个角的和是1800,那么称这两个角互为补角。
②类似的,如图2.1-3,∠1+∠2=90°,如果两个角的和是900,那么称这两个角互为余角。
活动:插入一段微视频,通过形象的flash动画,让学生在轻松幽默的学习气氛中再次体会“互余互补”的数量关系。
〖练习〗1.下列图中,哪些角互为余角?哪些角互为补角?
2.下列说法中,正确的有 。(填序号)
①若∠1+∠2+∠3=180 ,则∠1、∠2、∠3互补
②若∠A=40 26′,则∠A的余角=49 34′
③一个角的补角必为钝角。
活动目的:通过观察图形和观看微视频两种不同的形式,体验“互补互余”仅仅表明了两个角的度量关系,并没有限制角的位置关系,使学生在轻松幽默的气氛中学习知识。小练习再次巩固了学生对余角和补角的认识。
活动注意事项:教师首先应关注全体学生是否积极思考?及时关注学习上稍微落后的学生,对于简单的问题,在集体展示时给这部分同学展示的机会,可以极大的调动这部分同学的学习热情!
第三环节 学以致用,步步为营
问题4:如图2.1-4,打台球时,选择适当的方向,用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,将图2.1—7抽象成图2.1—8,ON与DC交于点O,∠DON=∠CON=900,∠1=∠2
小组合作交流,解决下列问题:在图2.1-5中
问题1:哪些角互为补角?哪些角互为余角?
问题2:∠3与∠4有什么关系?为什么?
问题3:∠AOC与∠BOD有什么关系?为什么?
你还能得到哪些结论?
活动目的:概括归纳得到猜想和规律,并加以验证,是学习数学的重要方法。通过生动有趣的活动情景,为学生提供了观察、推理、交流等丰富的数学活动,使学生在自主学习的过程中,掌握“同角或者等角的补角相等。”“同角或者等角的余角相等。”并能够用自己的语言说出简单推理。同时发散学生思维,让学生尽可能用多种方法来说明自己猜测的正确性,培养学生合情说理的能力。并在这个过程中,培养学生抽象几何图形进行建模的能力。本着面向全体的原则,从学生生活经验和熟悉的背景知识出发,通过创设情境串---问题串,极大的调动全体学生的参与意识,充分挖掘他们的潜能,给学生一个充分思考的机会,鼓励学生积极发言!
活动注意事项: 学生应有足够的时间和空间经历观察、猜测、推理、验证等活动过程。本环节的三个问题是环环紧扣、层层递进提出来的,前一个问题为下一个问题作好铺垫。在学习的过程中,时刻不能忘记学生是主体,一切教学活动都应当从学生已有的认知角度出发,问题环节设计跨越性不能太强,让学生在不断的探索过程中得到不同程度的感悟,自己能够主动地去探究问题的实质,体验成功的喜悦;教师要充分发散学生的思维,鼓励学生各抒己见,敢于质疑;上课要渗透合情说理的方法,进一步培养学生的推理能力。
第四环节 拓展延伸,综合应用
〖练习〗
1. ① 因为∠1+∠2=90 ,∠2+∠3=90 ,所以∠1= ,
理由是 .
② 因为∠1+∠2=180 ,∠2+∠3=180 ,所以∠1= , 理由是 .
2. 如图2.1-6已知:直线AB与CD交于点O,∠COE=900,回答下列问题:
(1)∠AOE的余角是_ ________;补角是_________。
(2)∠AOD的余角是________;补角是________;
对顶角是________。
3.如图2.1-7,直线AB、CD相交于点O,若∠BOD=42°,OA平分∠COE,求∠DOE的度数.
4.若一个角的补角等于它的余角的4倍,求这个角的度数.
5.如图2.1-8,已知直线AB、CD相交于点O,∠COE=90°.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD∶∠BOC=1∶5,求∠AOE的度数.
活动目的:通过一系列的巩固练习,可以让学生对本节的知识有更深一层的理解,也能培养学生应用知识的能力。练习题量不大,旨在对学生基本知识,基本方法,基本数学思想的运用,不加重学生的学习负担。同时习题各有侧重,锻炼学生的学习能力。具体课堂活动中,可以根据课堂效果和课堂时间,有选择、有针对性的练习。
活动的注意事项:鼓励学生自己分析问题,明晰思路,能够有条理的阐述问题,解决问题。对于学生的发言要及时肯定,有问题的地方可以先让学生自己小组合作谈论,教师予以一定引导。总而言之,希望学生能自己运用学习的知识解决问题,激发学生对数学的学习兴趣与信心,对出现的错误,一定进行积极的辨析,让学生学会解决的方法。
第五环节 学有所思 反馈巩固
归纳总结:
1. 你学到了哪些知识点?
2. 你学到了哪些方法?
3. 你还有哪些困惑?
活动目的:本环节的设置使学生学会从系统的角度把握知识方法,努力使知识结构化、网络化,引导学生时刻注意新旧知识之间的联系;鼓励学生畅谈自己学习的知识和体会,激发学生对数学的学习兴趣与信心,培养学生独自梳理知识,归纳学习方法及解题方法的能力。锻炼学生组织语言及表达能力,经历与同伴分享成果的快乐过程。
活动注意事项:教师一定让学生畅谈自己的切身感受,对于知识点的整合,更要有所思考,达到对所学知识巩固的目的。鼓励其他学生进行补充纠正,教师也应进行适时的点拨和强调。
四、教学设计反思:
1.注重数学与生活的联系
数学来源于生活,反之又服务于生活。本课时我从身边熟悉的情境出发,使学生经历从现实生活中抽象出数学模型的过程,体会本节课的重要性和在生活中的广泛应用。“几何直觉是增进数学理解力的很有效的途径,而且它可以使人增加勇气,提高修养。”通过动手操作,可以加深学生对知识的理解,从中发现知识。
2. 引入微视频,将信息技术与课堂融合
在课堂中引入一段微视频,生动幽默的语言和形象的flash动画,深深吸引着同学们,让学生们在轻松愉快的气氛中学习了有关的数学概念,再加之相应的课堂小练习,提高了学生的学习效率。
3.巧设问题串 打造高效课堂
我在教材提供的教学素材的基础上,恰当地创设情境,以问题串的方式激发学生的好奇心和求知欲,通过独立思考,不断提出问题分析问题,并创造性地解决问题,通过合作交流的方式,为学生构建了开放有效的学习环境。课堂习题的设置,题目由易到难,由简到繁,争取能让每一位学生都能领略到成功的喜悦!使学生思维分层递进,揭示概念的实质,不断完善新的知识结构,同时体验了知识的形成过程和发现的快乐,继而转化为进一步探索的内驱力;鼓励学生从多角度思考问题,充分激发学生的创新能力,使学生的思维多向开花,极大的调动学生学习数学的热情!
4.注意事项。
课堂上让学生充分发表自己的见解。教师应注意捕捉有效信息,从激励学生的角度出发,给予学生一个充分展示自我的舞台,在活动中提高学生与他人合作交流的能力,激发学生的学习兴趣。针对不同的问题,应大胆放手给学生,注意培养学生抽象几何图形的能力,简单合情说理的能力,观察分析的能力,总结归纳的能力等。讨论时,应该留给学生充分的独立思考的时间,不要让一些思维活跃的学生的回答代替了其他学生的思考,掩盖了其他学生的疑问。教师应注重学生几何语言的培养,对课堂生成的问题,应予以重视,教师可以激励学生课后继续探究,将课内学习延伸到课外,开阔学生的视野。
图2.1-1
图2.1-2
图2.1-2
图2.1-3
图2.1-4
2
D
C
O
1
3
4
A
N
B
图2.1-5
同角或者等角的余角相等。
同角或者等角的补角相等。
B
A
C
D
O
E
图2.1—6
图2.1-7
图2.1-8
PAGE
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
