北师大版八年级数学下册3.2 《图形的旋转》 同步练习(word,含答案)
文档属性
| 名称 | 北师大版八年级数学下册3.2 《图形的旋转》 同步练习(word,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 503.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-14 10:40:29 | ||
图片预览




文档简介
《3.2 图形的旋转》衔接中考
三年模拟全练
1.(2020河南郑州宇华教育集团第一次月考,6,★☆☆)如图,在正方形网格中,将△ABC绕点A旋转后得到△ADE,则下列旋转方式中,符合题意的是( )
A.逆时针旋转90°
B.顺时针旋转90°
C.逆时针旋转45°
D.顺时针旋转45°
2.(2020广东佛山映月中学第一阶段考,8,★☆☆)如图,将△ABC绕点A逆时针旋转100°得到△ADE.若点D在线段BC的延长线上,则∠B的大小为( )
A.30°
B.40°
C.50°
D.60°
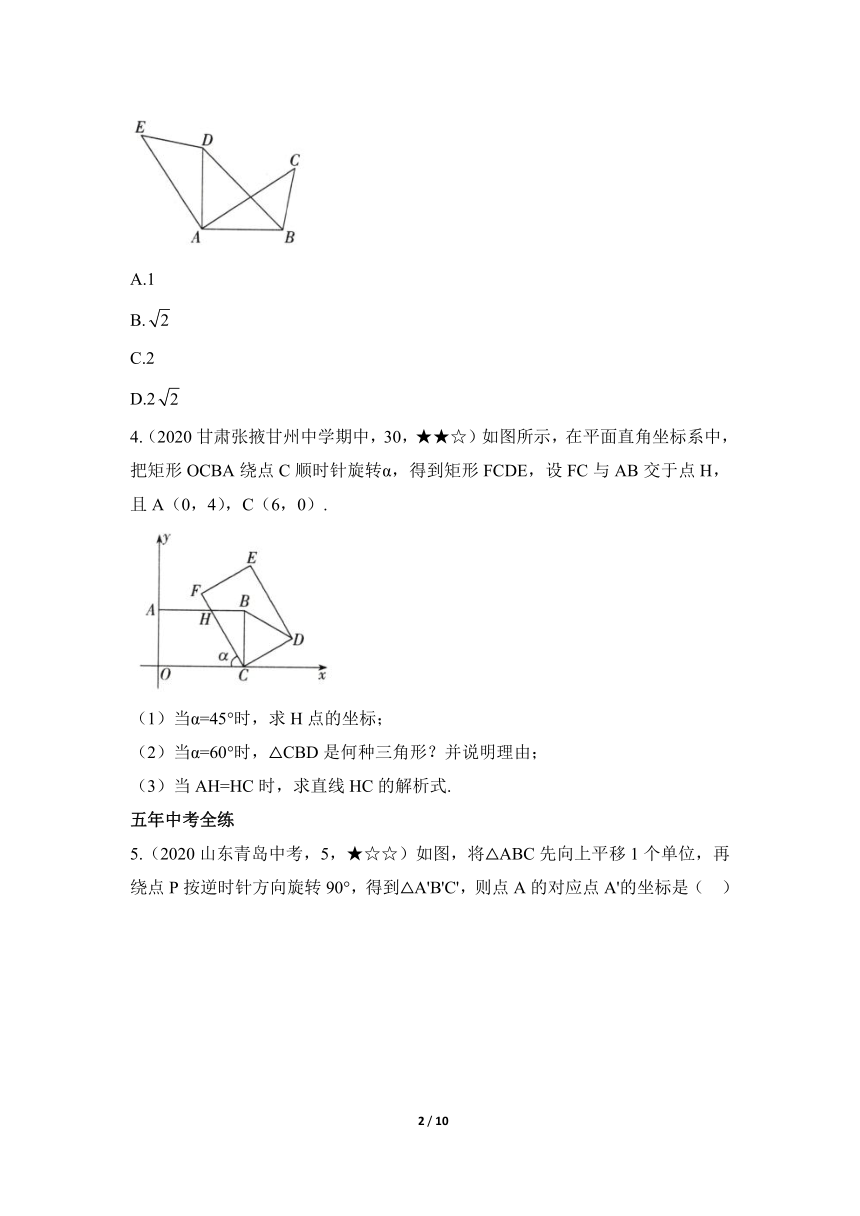
3.(2020山西太原期中,14,★★☆)如图,将△ABC绕点A逆时针旋转90°得到△ADE,点B,C的对应点分别为点D,E,AB=1,则BD的长为( )
A.1
B.
C.2
D.2
4.(2020甘肃张掖甘州中学期中,30,★★☆)如图所示,在平面直角坐标系中,把矩形OCBA绕点C顺时针旋转α,得到矩形FCDE,设FC与AB交于点H,且A(0,4),C(6,0).
(1)当α=45°时,求H点的坐标;
(2)当α=60°时,△CBD是何种三角形?并说明理由;
(3)当AH=HC时,求直线HC的解析式.
五年中考全练
5.(2020山东青岛中考,5,★☆☆)如图,将△ABC先向上平移1个单位,再绕点P按逆时针方向旋转90°,得到△A'B'C',则点A的对应点A'的坐标是( )
A.(0,4)
B.(2,-2)
C.(3,-2)
D.(-1,4)
6.(2020山东枣庄中考,10,★★☆)如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是( )
A.(-,3)
B(-3,)
C.(-,2+)
D.(-1,2+)
7.(2020山东潍坊中考,24,★★★)如图①,在△ABC中,∠A=90°,AB=AC=+1,点D,E分别在边AB,AC上,且AD=AE=1,连接DE.现将△ADE绕点A顺时针方向旋转,旋转角为α(0°<α<360°),如图②,连接CE,BD,CD.
(1)当0°<α<180°时,求证:CE=BD;
(2)如图③,当α=90°时,延长CE交BD于点F,求证:CF垂直平分BD;
(3)在旋转过程中,求△BCD的面积的最大值,并写出此时旋转角α的度数.
核心素养全练
8.(2020山东滕州鲍沟中学)如图,在平面直角坐标系xOy中,已知A,B(0,4),将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去,……,则点B2019的横坐标为( )
A.10090
B.10096
C.0
D.4
9.(2020山东滨州中考,20,★★☆)如图,点P是正方形ABCD内一点,且点P到点A、B、C的距离分别为2、、4,则正方形ABCD的面积为__________.
参考答案
1.答案:A
解析:根据题中图形可知,将△ABC绕点A逆时针旋转90°可得到△ADE,故选A.
2.答案:B
解析:∵△ADE是由△ABC绕点A旋转100°得到的,
∴∠BAD=100°,AD=AB,
∵点D在BC的延长线上,
∴∠B=∠ADB=.
故选B.
3.答案:B
解析:由旋转的性质可知AD=AB=1,∠BAD=90°,
∴BD=,故选B.
4.答案:见解析
解析:(1)∵A(0,4),C(6,0),四边形OCBA为矩形,
∴OA=BC=4,AB=OC=6,
∴α=45°,∠ABC=90°,
∴△HBC是等腰直角三角形,BH=BC=4,
∴AH=AB-BH=6-4=2,
∴H点的坐标为(2,4).
(2)△CBD为等边三角形.
理由如下:∵α=60°,
∴∠BCD=α=60°.
又∵BC=DC,
∴△CBD为等边三角形.
(3)设AH=CH=x,则在Rt△BCH中,由勾股定理可得,解得.故.
设直线HC的解析式为y=kx+b(k≠0),则有,解得,
∴直线HC的解析式为y=.
5.答案:D
解析:由题图可知点A的坐标为(4,2),向上平移一个单位后对应点的坐标为(4,3),再绕点P按逆时针方向旋转90°后对应点的坐标为(-1,4),如图所示.
6.答案:A
解析:如图,过点B'作B'H⊥y轴于H.
由旋转的性质可知,∠AOB=∠A'OB'=30°,
∠B=∠A'B'O=30°,AB=OA=A'B'=A'O=2,
在Rt△A'B'H中,∵A'B'=2,∠B'A'H=60°,
∴∠A'B'H=30°,
∴,
∴OH=OA'+A'H=2+1=3,∴B'的坐标是(-,3),故选A.
7.答案:见解析
解析:(1)证明:由旋转知∠CAE=∠BAD=α.
在△ACE和△ABD中,,
∴△ACE≌△ABD(SAS),
∴CE=BD.
(2)证明:由(1)知△ACE≌△ABD,∴∠ACE=∠ABD.
∵∠ACE+∠AEC=90°,∠AEC=∠FEB,
∴∠ABD+∠FEB=90°,∴∠EFB=90°,∴CF⊥BD.
∵AB=AC=+1,AD=AE=1,∠CAB=∠EAD=90°,
∴BC=AB=+2,CD=AC+AD=+2,∴BC=CD.
∵CF⊥BD,∴CF垂直平分BD.
(3)在△BCD中,边BC的长是定值,则BC边上的高取最大值时△BCD的面积有最大值.
∵点D的轨迹是以点A为圆心,AD长为半径的圆,
∴当点D在线段BC的垂直平分线AG(D在A的左侧)上时,△BCD的面积取得最大值,如图.
∵AB=AC=+1,AD=AE=1,∠CAB=∠EAD=90°,DG⊥BC于G,
∴,
∴DG=AG+AD=,∠DAB=90°+45°=135°,
∴S△BCD的最大值为,
此时旋转角α=135°.
8.答案:B
解析:在Rt△ABO中,OA=,OB=4,∴AB=.
∴AO+OB+AB=,∴B2的横坐标为10,B4的横坐标为20,......,
∴B2020的横坐标为10=10100,∴B2019的横坐标为10100-4=10096,故选B.
9.答案:14+4
解析:如图,将△ABP绕点B顺时针旋转90°得到△CBM,连接PM,过点B作BH⊥PM于H.
∵BP=BM=,∠PBM=90°,
∴PM=PB=2,
∵PC=4,PA=CM=2,
∴PC =CM +PM ,
∴∠PMC=90°,
∵∠BPM=∠BMP=45°,
∴∠CMB=∠APB=135°,
∴∠APB+∠BPM=180°
∴A,P,M三点共线,
∵BH⊥PM,∴PH=HM,
∴BH=PH=HM=1,
∴AH=2+1,
∴AB =AH +BH =(2+1) +1 =14+4,
∴正方形ABCD的面积为14+4.
故答案为14+4.
1 / 10
三年模拟全练
1.(2020河南郑州宇华教育集团第一次月考,6,★☆☆)如图,在正方形网格中,将△ABC绕点A旋转后得到△ADE,则下列旋转方式中,符合题意的是( )
A.逆时针旋转90°
B.顺时针旋转90°
C.逆时针旋转45°
D.顺时针旋转45°
2.(2020广东佛山映月中学第一阶段考,8,★☆☆)如图,将△ABC绕点A逆时针旋转100°得到△ADE.若点D在线段BC的延长线上,则∠B的大小为( )
A.30°
B.40°
C.50°
D.60°
3.(2020山西太原期中,14,★★☆)如图,将△ABC绕点A逆时针旋转90°得到△ADE,点B,C的对应点分别为点D,E,AB=1,则BD的长为( )
A.1
B.
C.2
D.2
4.(2020甘肃张掖甘州中学期中,30,★★☆)如图所示,在平面直角坐标系中,把矩形OCBA绕点C顺时针旋转α,得到矩形FCDE,设FC与AB交于点H,且A(0,4),C(6,0).
(1)当α=45°时,求H点的坐标;
(2)当α=60°时,△CBD是何种三角形?并说明理由;
(3)当AH=HC时,求直线HC的解析式.
五年中考全练
5.(2020山东青岛中考,5,★☆☆)如图,将△ABC先向上平移1个单位,再绕点P按逆时针方向旋转90°,得到△A'B'C',则点A的对应点A'的坐标是( )
A.(0,4)
B.(2,-2)
C.(3,-2)
D.(-1,4)
6.(2020山东枣庄中考,10,★★☆)如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B'的坐标是( )
A.(-,3)
B(-3,)
C.(-,2+)
D.(-1,2+)
7.(2020山东潍坊中考,24,★★★)如图①,在△ABC中,∠A=90°,AB=AC=+1,点D,E分别在边AB,AC上,且AD=AE=1,连接DE.现将△ADE绕点A顺时针方向旋转,旋转角为α(0°<α<360°),如图②,连接CE,BD,CD.
(1)当0°<α<180°时,求证:CE=BD;
(2)如图③,当α=90°时,延长CE交BD于点F,求证:CF垂直平分BD;
(3)在旋转过程中,求△BCD的面积的最大值,并写出此时旋转角α的度数.
核心素养全练
8.(2020山东滕州鲍沟中学)如图,在平面直角坐标系xOy中,已知A,B(0,4),将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去,……,则点B2019的横坐标为( )
A.10090
B.10096
C.0
D.4
9.(2020山东滨州中考,20,★★☆)如图,点P是正方形ABCD内一点,且点P到点A、B、C的距离分别为2、、4,则正方形ABCD的面积为__________.
参考答案
1.答案:A
解析:根据题中图形可知,将△ABC绕点A逆时针旋转90°可得到△ADE,故选A.
2.答案:B
解析:∵△ADE是由△ABC绕点A旋转100°得到的,
∴∠BAD=100°,AD=AB,
∵点D在BC的延长线上,
∴∠B=∠ADB=.
故选B.
3.答案:B
解析:由旋转的性质可知AD=AB=1,∠BAD=90°,
∴BD=,故选B.
4.答案:见解析
解析:(1)∵A(0,4),C(6,0),四边形OCBA为矩形,
∴OA=BC=4,AB=OC=6,
∴α=45°,∠ABC=90°,
∴△HBC是等腰直角三角形,BH=BC=4,
∴AH=AB-BH=6-4=2,
∴H点的坐标为(2,4).
(2)△CBD为等边三角形.
理由如下:∵α=60°,
∴∠BCD=α=60°.
又∵BC=DC,
∴△CBD为等边三角形.
(3)设AH=CH=x,则在Rt△BCH中,由勾股定理可得,解得.故.
设直线HC的解析式为y=kx+b(k≠0),则有,解得,
∴直线HC的解析式为y=.
5.答案:D
解析:由题图可知点A的坐标为(4,2),向上平移一个单位后对应点的坐标为(4,3),再绕点P按逆时针方向旋转90°后对应点的坐标为(-1,4),如图所示.
6.答案:A
解析:如图,过点B'作B'H⊥y轴于H.
由旋转的性质可知,∠AOB=∠A'OB'=30°,
∠B=∠A'B'O=30°,AB=OA=A'B'=A'O=2,
在Rt△A'B'H中,∵A'B'=2,∠B'A'H=60°,
∴∠A'B'H=30°,
∴,
∴OH=OA'+A'H=2+1=3,∴B'的坐标是(-,3),故选A.
7.答案:见解析
解析:(1)证明:由旋转知∠CAE=∠BAD=α.
在△ACE和△ABD中,,
∴△ACE≌△ABD(SAS),
∴CE=BD.
(2)证明:由(1)知△ACE≌△ABD,∴∠ACE=∠ABD.
∵∠ACE+∠AEC=90°,∠AEC=∠FEB,
∴∠ABD+∠FEB=90°,∴∠EFB=90°,∴CF⊥BD.
∵AB=AC=+1,AD=AE=1,∠CAB=∠EAD=90°,
∴BC=AB=+2,CD=AC+AD=+2,∴BC=CD.
∵CF⊥BD,∴CF垂直平分BD.
(3)在△BCD中,边BC的长是定值,则BC边上的高取最大值时△BCD的面积有最大值.
∵点D的轨迹是以点A为圆心,AD长为半径的圆,
∴当点D在线段BC的垂直平分线AG(D在A的左侧)上时,△BCD的面积取得最大值,如图.
∵AB=AC=+1,AD=AE=1,∠CAB=∠EAD=90°,DG⊥BC于G,
∴,
∴DG=AG+AD=,∠DAB=90°+45°=135°,
∴S△BCD的最大值为,
此时旋转角α=135°.
8.答案:B
解析:在Rt△ABO中,OA=,OB=4,∴AB=.
∴AO+OB+AB=,∴B2的横坐标为10,B4的横坐标为20,......,
∴B2020的横坐标为10=10100,∴B2019的横坐标为10100-4=10096,故选B.
9.答案:14+4
解析:如图,将△ABP绕点B顺时针旋转90°得到△CBM,连接PM,过点B作BH⊥PM于H.
∵BP=BM=,∠PBM=90°,
∴PM=PB=2,
∵PC=4,PA=CM=2,
∴PC =CM +PM ,
∴∠PMC=90°,
∵∠BPM=∠BMP=45°,
∴∠CMB=∠APB=135°,
∴∠APB+∠BPM=180°
∴A,P,M三点共线,
∵BH⊥PM,∴PH=HM,
∴BH=PH=HM=1,
∴AH=2+1,
∴AB =AH +BH =(2+1) +1 =14+4,
∴正方形ABCD的面积为14+4.
故答案为14+4.
1 / 10
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
