北师大版八年级数学下册3.3中心对称 学案(无答案)
文档属性
| 名称 | 北师大版八年级数学下册3.3中心对称 学案(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 118.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-14 23:24:52 | ||
图片预览

文档简介
§3.3 中心对称
【学习目标】
1.通过具体实例了解中心对称,中心对称图形的概念,探索它的基本性质;
2.经历有关中心对称的观察、操作、欣赏和设计的过程,能概括出中心对称的基本性质,能利用中心对称的性质去解决问题,进一步积累数学活动经验,增强动手实践能力,发展空间概念;
3.认识并欣赏自然界和现实生活中的中心对称图形.
【学习重难点】
学习重点:
理解中心对称和中心对称图形的定义和基本性质,并会进行中心对称作图.
学习难点:
探索中心对称的性质,并且能利用性质作图、解决实际问题.
【学习流程】
环节一:回顾与思考
复习七下第五章轴对称变换和本章学移与旋转进行对比学习.
欣赏生活中轴对称、旋转变换的美图并复习相关知识.
环节二:新知探究(中心对称)
引入新知:
几何画板动态演示旋转不同角度后△ABC的大小位置变化;
特别观察三角形旋转180°之后,与另一个三角形的关系.
概念明晰:
像这样把一个图形绕着某一点旋转180°,如果它能够和另一个图形重合,那么,我们就称这两个图形关于这个点对称或中心对称.
注:中心对称是两个图形的特殊位置关系!!!
中心对称是一种特殊的_________,因此它具有___________的一切性质.
性质探究:
自己画一个图形(如三角形),选取一个旋转中心,把所画的图形绕旋转中心旋转180°.
操作完成后回答下列问题:
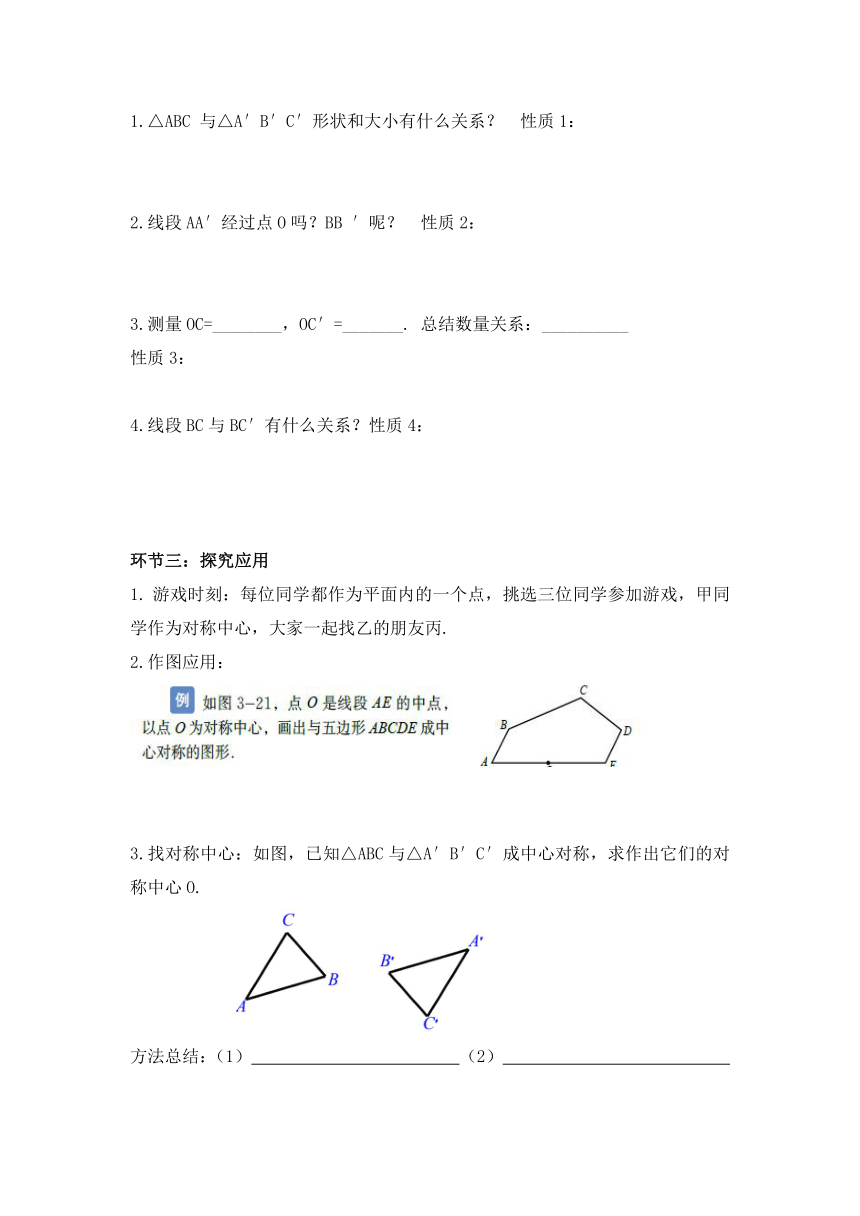
1.△ABC 与△A′B′C′形状和大小有什么关系? 性质1:
2.线段AA′经过点O吗?BB ′呢? 性质2:
3.测量OC=________,OC′=_______. 总结数量关系:__________
性质3:
4.线段BC与BC′有什么关系?性质4:
环节三:探究应用
游戏时刻:每位同学都作为平面内的一个点,挑选三位同学参加游戏,甲同学作为对称中心,大家一起找乙的朋友丙.
2.作图应用:
3.找对称中心:如图,已知△ABC与△A′B′C′成中心对称,求作出它们的对称中心O.
方法总结:(1) (2)
环节四:对比探究(中心对称图形)
对比学习:一个图形至少旋转多少度与原图形重合?
概念明晰:
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做 ;这个点叫做它的 ;互相重合的点叫做 _。
注:中心对称图形是一个图形的性质特征!!!
概念辨析:
1.中心对称和中心对称图形的区别与联系
中心对称 中心对称图形
区别
联系
2.轴对称与中心对称的区别与联系
轴对称 中心对称
环节五:学以致用
1.观察常见的几何图形,并回答下面的问题:
(1)哪些只是轴对称图形?
(2)哪些只是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?
2.在26个英文大写正体字母中,哪些字母是中心对称图形
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
环节六:回归生活
揭秘魔术
美图欣赏
设计美图
(1)运用中心对称,可以糅合轴对称、平移、旋转知识;
(2)富有创造性、艺术性和象征意义.
环节七:颗粒归仓
获?
惑?
环节八:作业布置
必做:
习题3.5(知识技能+数学理解+问题解决)
选做:
拓展提升:如图,矩形ABCD的对角线AC 和BD 相交 于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为多少?
学习检测(课后)
1.四边形ABCD的对角线相交于O,且AO=BO=CO=DO,则这个四边形( )
A.仅是轴对称图形
B.仅是中心对称图形
C.既是轴对称图形又是中心对称图形
D.既不是轴对称图形,又不是中心对称图形
2.如图,在Rt△ABC中,斜边AB长为8,直角边BC长为12,若扇形ACE与扇形BDE关于点E中心对称,则图中阴影部分的面积约为( )
A.27 B.42 C.56 D.108
3.在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B20A21B21的顶点A21的坐标是 .
4.如图,把平面直角坐标系xOy中的△ABC经过一定的变换得到△A′B′C′,若△ABC内有一点P的坐标为(-2,-2),那么它的对应点P′的坐标为( )
A.(-4,-2)B.(0,-2)C.(0,2)D.(4,2)
【学习目标】
1.通过具体实例了解中心对称,中心对称图形的概念,探索它的基本性质;
2.经历有关中心对称的观察、操作、欣赏和设计的过程,能概括出中心对称的基本性质,能利用中心对称的性质去解决问题,进一步积累数学活动经验,增强动手实践能力,发展空间概念;
3.认识并欣赏自然界和现实生活中的中心对称图形.
【学习重难点】
学习重点:
理解中心对称和中心对称图形的定义和基本性质,并会进行中心对称作图.
学习难点:
探索中心对称的性质,并且能利用性质作图、解决实际问题.
【学习流程】
环节一:回顾与思考
复习七下第五章轴对称变换和本章学移与旋转进行对比学习.
欣赏生活中轴对称、旋转变换的美图并复习相关知识.
环节二:新知探究(中心对称)
引入新知:
几何画板动态演示旋转不同角度后△ABC的大小位置变化;
特别观察三角形旋转180°之后,与另一个三角形的关系.
概念明晰:
像这样把一个图形绕着某一点旋转180°,如果它能够和另一个图形重合,那么,我们就称这两个图形关于这个点对称或中心对称.
注:中心对称是两个图形的特殊位置关系!!!
中心对称是一种特殊的_________,因此它具有___________的一切性质.
性质探究:
自己画一个图形(如三角形),选取一个旋转中心,把所画的图形绕旋转中心旋转180°.
操作完成后回答下列问题:
1.△ABC 与△A′B′C′形状和大小有什么关系? 性质1:
2.线段AA′经过点O吗?BB ′呢? 性质2:
3.测量OC=________,OC′=_______. 总结数量关系:__________
性质3:
4.线段BC与BC′有什么关系?性质4:
环节三:探究应用
游戏时刻:每位同学都作为平面内的一个点,挑选三位同学参加游戏,甲同学作为对称中心,大家一起找乙的朋友丙.
2.作图应用:
3.找对称中心:如图,已知△ABC与△A′B′C′成中心对称,求作出它们的对称中心O.
方法总结:(1) (2)
环节四:对比探究(中心对称图形)
对比学习:一个图形至少旋转多少度与原图形重合?
概念明晰:
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做 ;这个点叫做它的 ;互相重合的点叫做 _。
注:中心对称图形是一个图形的性质特征!!!
概念辨析:
1.中心对称和中心对称图形的区别与联系
中心对称 中心对称图形
区别
联系
2.轴对称与中心对称的区别与联系
轴对称 中心对称
环节五:学以致用
1.观察常见的几何图形,并回答下面的问题:
(1)哪些只是轴对称图形?
(2)哪些只是中心对称图形?
(3)哪些既是轴对称图形,又是中心对称图形?
2.在26个英文大写正体字母中,哪些字母是中心对称图形
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
环节六:回归生活
揭秘魔术
美图欣赏
设计美图
(1)运用中心对称,可以糅合轴对称、平移、旋转知识;
(2)富有创造性、艺术性和象征意义.
环节七:颗粒归仓
获?
惑?
环节八:作业布置
必做:
习题3.5(知识技能+数学理解+问题解决)
选做:
拓展提升:如图,矩形ABCD的对角线AC 和BD 相交 于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为多少?
学习检测(课后)
1.四边形ABCD的对角线相交于O,且AO=BO=CO=DO,则这个四边形( )
A.仅是轴对称图形
B.仅是中心对称图形
C.既是轴对称图形又是中心对称图形
D.既不是轴对称图形,又不是中心对称图形
2.如图,在Rt△ABC中,斜边AB长为8,直角边BC长为12,若扇形ACE与扇形BDE关于点E中心对称,则图中阴影部分的面积约为( )
A.27 B.42 C.56 D.108
3.在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B20A21B21的顶点A21的坐标是 .
4.如图,把平面直角坐标系xOy中的△ABC经过一定的变换得到△A′B′C′,若△ABC内有一点P的坐标为(-2,-2),那么它的对应点P′的坐标为( )
A.(-4,-2)B.(0,-2)C.(0,2)D.(4,2)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
