北师大版八年级数学下册 第三章图形的平移与旋转复习(第1课时)学案 (无答案)
文档属性
| 名称 | 北师大版八年级数学下册 第三章图形的平移与旋转复习(第1课时)学案 (无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 651.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-15 00:00:00 | ||
图片预览

文档简介
第三章《图形的平移与旋转》回顾与思考 学案
一、学习目标
1.通过平滑火车和摩天轮的实例,能说出平移与旋转性质的具体内容,进而发展空间观念.
2.通过独立思考,合作交流的活动,能根据平移与旋转性质正确计算角度和线段长度,归纳出特殊三角形存在条件,体会从特殊到一般再到特殊的数学思想.
3.通过能力提升活动,体会半角模型思想.
重点:平移与旋转性质应用.
难点:通过旋转构造全等三角形,体会半角模型思想.
二、学习过程
(一)情景引入
观察郑州方特乐园,写出平移与旋转性质的具体内容
平移两要素: 平移性质内容:
旋转三要素: 旋转性质内容:
(二)平移性质的探究
小明将Rt△ABC,∠B=90°,沿BC向右平移到如图1的位置,得到Rt△DCE,使平移后点B与点C重合,CB=3,∠A=30°.
(1)请你求出平移的距离 ;
(2)线段AD,BC,CE分别是对应点所连线段它们之间有怎样的关系?
(3)CE= ,DE= ,CD= .
(4)判断线段AB与CD,AC与DE,BC与CE的位置关系?
(5)∠D= ,∠ACB= .
小试牛刀
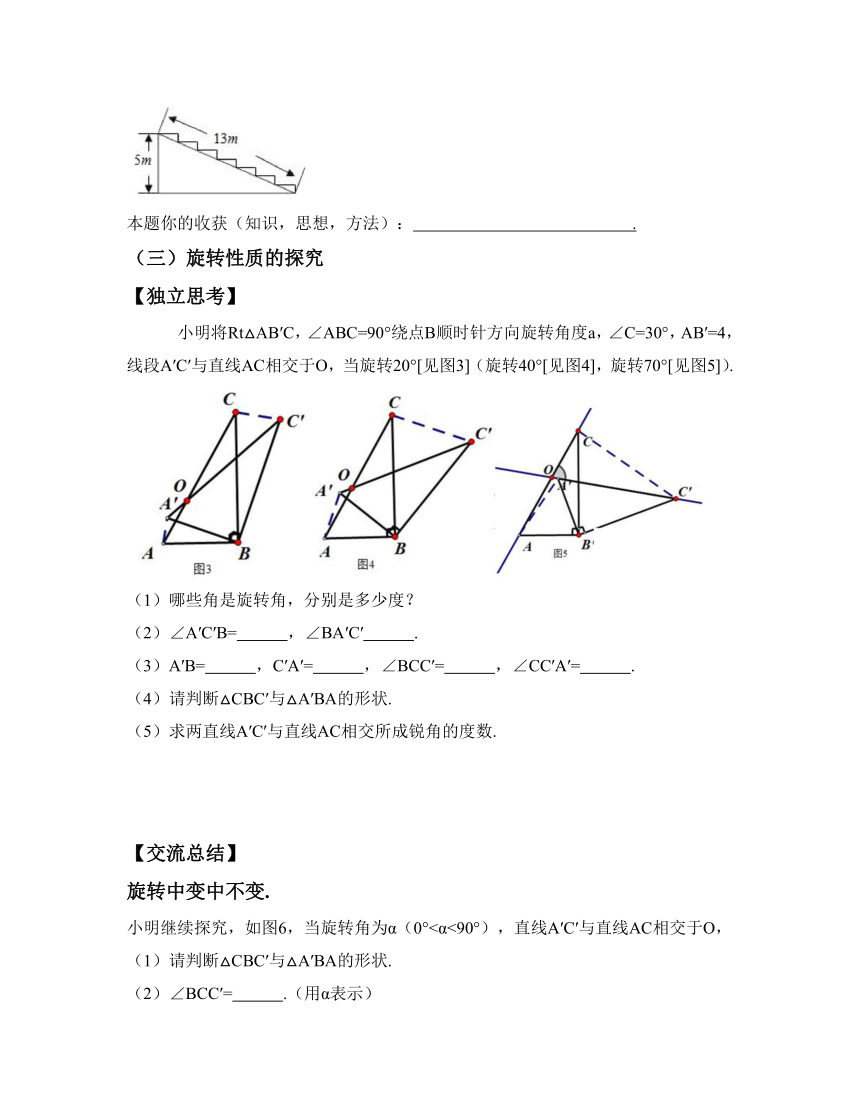
某酒店打算在一段楼梯面上铺地毯,如图2所示,求所铺地毯的长?
本题你的收获(知识,思想,方法): .
(三)旋转性质的探究
【独立思考】
小明将Rt△AB′C,∠ABC=90°绕点B顺时针方向旋转角度a,∠C=30°,AB′=4,线段A′C′与直线AC相交于O,当旋转20°[见图3](旋转40°[见图4],旋转70°[见图5]).
(1)哪些角是旋转角,分别是多少度?
(2)∠A′C′B= ,∠BA′C′ .
(3)A′B= ,C′A′= ,∠BCC′= ,∠CC′A′= .
(4)请判断△CBC′与△A′BA的形状.
(5)求两直线A′C′与直线AC相交所成锐角的度数.
【交流总结】
旋转中变中不变.
小明继续探究,如图6,当旋转角为α(0°<α<90°),直线A′C′与直线AC相交于O,
(1)请判断△CBC′与△A′BA的形状.
(2)∠BCC′= .(用α表示)
(3)求两直线A′C′与直线AC相交所成锐角的度数.(用α表示)
2.当旋转60°时,见图7
(1)哪些角是旋转角,分别是多少度?
(2)请判断△A′B′A与△C′B′C′的形状
(3)求两直线A′C′与直线AC相交所成锐角的度数.
3.当旋转90°时,见图8
(1)哪些角是旋转角,分别是多少度?
(2)请判断△A′BA与△C′BC′的形状.
(3)求两直线AC′与直线AC相交所成锐角的度数.
本题你的收获(知识,思想,方法): .
总结
方法:遇到旋转60°或90°的问题,常出现 .
(三)能力提升
如图,在四边形BC′B′D中,∠BC′B′=120°,C′B=C′B,∠B=∠B′=90°,且∠AC′E=60°,A、E分别是BD、B′D上的点,探究图中线段BA、AE、B′E之间的关系.
针对以上问题,小明的具体做法如图10:将Rt△ABC绕点C′逆时针方向旋转120°,得到Rt△A′C′B′. 所以,他说A′E=AE,因此得出AE=BA+B′E,你能说明理由么?
请写出证明过程.
【变式应用1】
如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,且∠EAF =∠BAD,A、E分别是BD、CD上的点,上述线段BE、EF、DF之间的结论是否仍然成立?说明理由.
本题你的收获(知识,思想,方法): .
三、课堂小结
说说你在知识,思想方法方面的收获与困惑.
四、作业布置
必做题:归纳整理学案的知识点及习题.
选做题:
已知:△ABC是等边三角形,P是三角形内一点,PA=3,PB=4,PC=5.
求:∠APB的度数.
一、学习目标
1.通过平滑火车和摩天轮的实例,能说出平移与旋转性质的具体内容,进而发展空间观念.
2.通过独立思考,合作交流的活动,能根据平移与旋转性质正确计算角度和线段长度,归纳出特殊三角形存在条件,体会从特殊到一般再到特殊的数学思想.
3.通过能力提升活动,体会半角模型思想.
重点:平移与旋转性质应用.
难点:通过旋转构造全等三角形,体会半角模型思想.
二、学习过程
(一)情景引入
观察郑州方特乐园,写出平移与旋转性质的具体内容
平移两要素: 平移性质内容:
旋转三要素: 旋转性质内容:
(二)平移性质的探究
小明将Rt△ABC,∠B=90°,沿BC向右平移到如图1的位置,得到Rt△DCE,使平移后点B与点C重合,CB=3,∠A=30°.
(1)请你求出平移的距离 ;
(2)线段AD,BC,CE分别是对应点所连线段它们之间有怎样的关系?
(3)CE= ,DE= ,CD= .
(4)判断线段AB与CD,AC与DE,BC与CE的位置关系?
(5)∠D= ,∠ACB= .
小试牛刀
某酒店打算在一段楼梯面上铺地毯,如图2所示,求所铺地毯的长?
本题你的收获(知识,思想,方法): .
(三)旋转性质的探究
【独立思考】
小明将Rt△AB′C,∠ABC=90°绕点B顺时针方向旋转角度a,∠C=30°,AB′=4,线段A′C′与直线AC相交于O,当旋转20°[见图3](旋转40°[见图4],旋转70°[见图5]).
(1)哪些角是旋转角,分别是多少度?
(2)∠A′C′B= ,∠BA′C′ .
(3)A′B= ,C′A′= ,∠BCC′= ,∠CC′A′= .
(4)请判断△CBC′与△A′BA的形状.
(5)求两直线A′C′与直线AC相交所成锐角的度数.
【交流总结】
旋转中变中不变.
小明继续探究,如图6,当旋转角为α(0°<α<90°),直线A′C′与直线AC相交于O,
(1)请判断△CBC′与△A′BA的形状.
(2)∠BCC′= .(用α表示)
(3)求两直线A′C′与直线AC相交所成锐角的度数.(用α表示)
2.当旋转60°时,见图7
(1)哪些角是旋转角,分别是多少度?
(2)请判断△A′B′A与△C′B′C′的形状
(3)求两直线A′C′与直线AC相交所成锐角的度数.
3.当旋转90°时,见图8
(1)哪些角是旋转角,分别是多少度?
(2)请判断△A′BA与△C′BC′的形状.
(3)求两直线AC′与直线AC相交所成锐角的度数.
本题你的收获(知识,思想,方法): .
总结
方法:遇到旋转60°或90°的问题,常出现 .
(三)能力提升
如图,在四边形BC′B′D中,∠BC′B′=120°,C′B=C′B,∠B=∠B′=90°,且∠AC′E=60°,A、E分别是BD、B′D上的点,探究图中线段BA、AE、B′E之间的关系.
针对以上问题,小明的具体做法如图10:将Rt△ABC绕点C′逆时针方向旋转120°,得到Rt△A′C′B′. 所以,他说A′E=AE,因此得出AE=BA+B′E,你能说明理由么?
请写出证明过程.
【变式应用1】
如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,且∠EAF =∠BAD,A、E分别是BD、CD上的点,上述线段BE、EF、DF之间的结论是否仍然成立?说明理由.
本题你的收获(知识,思想,方法): .
三、课堂小结
说说你在知识,思想方法方面的收获与困惑.
四、作业布置
必做题:归纳整理学案的知识点及习题.
选做题:
已知:△ABC是等边三角形,P是三角形内一点,PA=3,PB=4,PC=5.
求:∠APB的度数.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
