北师大版八年级数学下册 第三章 图形的平移与旋转 章末检测(word版 含解析)
文档属性
| 名称 | 北师大版八年级数学下册 第三章 图形的平移与旋转 章末检测(word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 646.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-15 07:15:20 | ||
图片预览


文档简介
《第三章 图形的平移与旋转》章末检测
选择题
1.(2019广东揭阳普宁期中)下列四个图案中,不能由1号图形平移得到2号图形的是( )
A.
B.
C.
D.
2.(2017山东泰安中考)如图所示的图案中,为中心对称图形的是( )
A.①②
B.②③
C.②④
D.③④
3.(2020湖北武汉青山期中)四根火柴棒摆成如图所示的象形“口”字,平移此象形字火柴棒后,变成的象形文字是( )
A.
B.
C.
D.
4.观察图中的三个图形,照此规律,可知第四个图形是( )
A.
B.
C.
D.
5.(2020广东佛山顺德期末)在平面直角坐标系中,将点A(-1,2)先向左平移2个单位长度,再向下平移3个单位长度后,得到的点的坐标为( )
A.(1,-1)
B.(-1,5)
C.(-3,-1)
D.(-3,5)
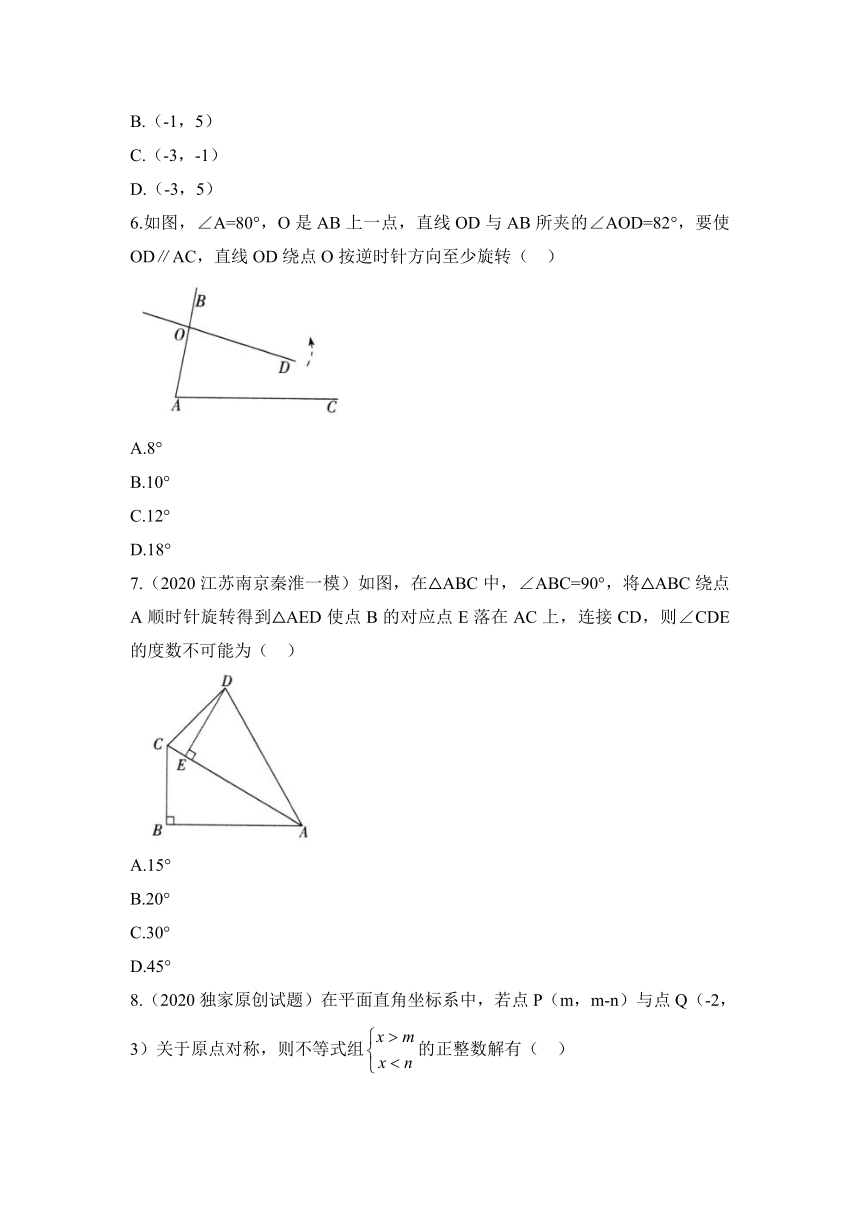
6.如图,∠A=80°,O是AB上一点,直线OD与AB所夹的∠AOD=82°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转( )
A.8°
B.10°
C.12°
D.18°
7.(2020江苏南京秦淮一模)如图,在△ABC中,∠ABC=90°,将△ABC绕点A顺时针旋转得到△AED使点B的对应点E落在AC上,连接CD,则∠CDE的度数不可能为( )
A.15°
B.20°
C.30°
D.45°
8.(2020独家原创试题)在平面直角坐标系中,若点P(m,m-n)与点Q(-2,3)关于原点对称,则不等式组的正整数解有( )
A.1个
B.2个
C.3个
D.4个
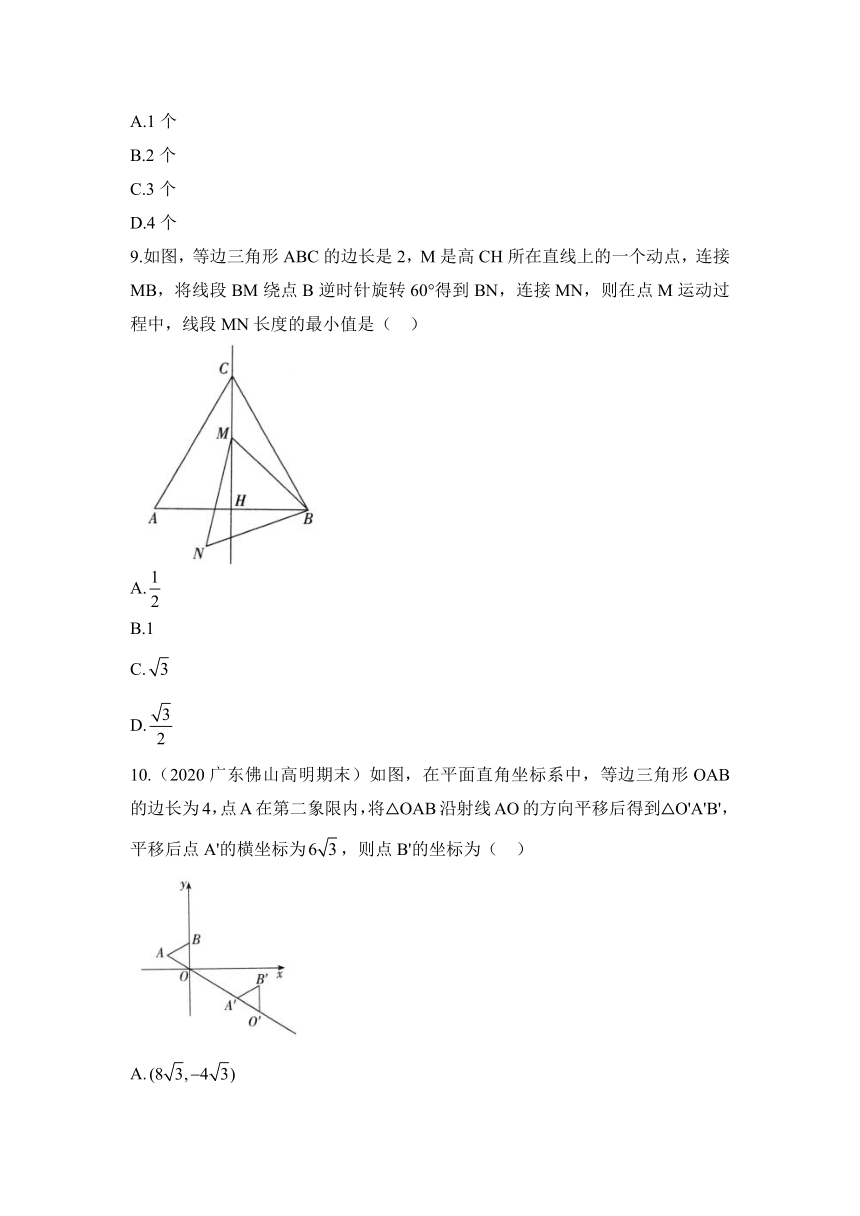
9.如图,等边三角形ABC的边长是2,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接MN,则在点M运动过程中,线段MN长度的最小值是( )
A.
B.1
C.
D.
10.(2020广东佛山高明期末)如图,在平面直角坐标系中,等边三角形OAB的边长为4,点A在第二象限内,将△OAB沿射线AO的方向平移后得到△O'A'B',平移后点A'的横坐标为,则点B'的坐标为( )
A.
B.
C.
D.(8,-4)
填空题
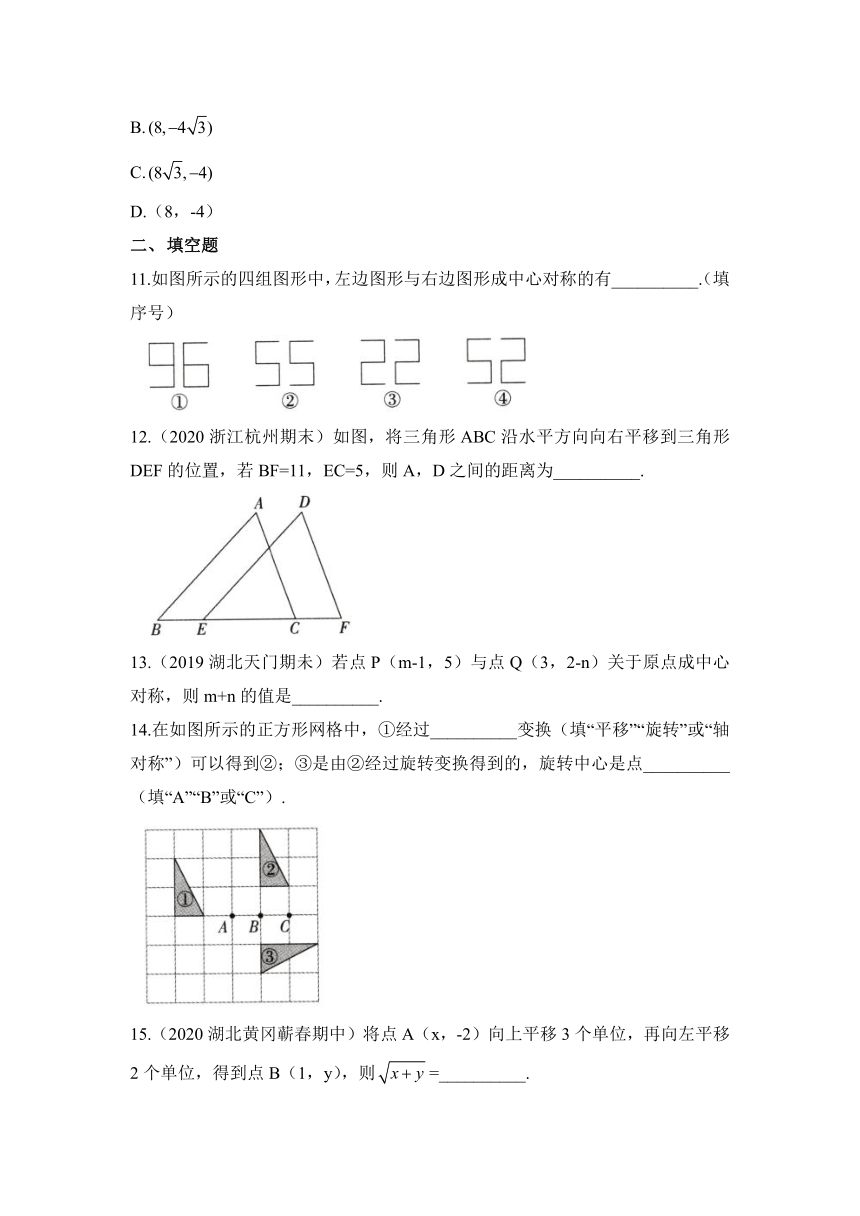
11.如图所示的四组图形中,左边图形与右边图形成中心对称的有__________.(填序号)
12.(2020浙江杭州期末)如图,将三角形ABC沿水平方向向右平移到三角形DEF的位置,若BF=11,EC=5,则A,D之间的距离为__________.
13.(2019湖北天门期未)若点P(m-1,5)与点Q(3,2-n)关于原点成中心对称,则m+n的值是__________.
14.在如图所示的正方形网格中,①经过__________变换(填“平移”“旋转”或“轴对称”)可以得到②;③是由②经过旋转变换得到的,旋转中心是点__________(填“A”“B”或“C”).
15.(2020湖北黄冈蕲春期中)将点A(x,-2)向上平移3个单位,再向左平移2个单位,得到点B(1,y),则=__________.
16.(2017辽宁鞍山中考)如图,在△ABC中,∠ACB=90°,AC=4,BC=3,将△ABC绕点A顺时针旋转得到△ADE(其中点B恰好落在AC延长线上点D处,点C落在点E处),连接BD,则四边形AEDB的面积为_________.
17.(2020四川广元模拟)如图,将△ABC绕点A旋转一定角度后得到△ADE.若∠CAE=60°,∠E=65°,且AD⊥BC,则∠BAC=__________°.
18.如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
①△AED≌△AEF;②BE+DC=DE;③BE +DC =DE ,其中正确的是__________.(填序号)
解答题
19.(10分)如图,已知AC⊥BC,垂足为C,AC=4,BC=,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.
(1)线段DC=___________;
(2)求线段DB的长度.
20.(2020安徽合肥包河一模)(9分)如图,在边长为1的小正方形组成的网格中,给出了格点△ABC(顶点为网格线的交点).
(1)将△ABC先向下平移3个单位长度,再向右平移4个单位长度得到△A1B1C1,画出平移后的图形;
(2)将△ABC绕点A1顺时针旋转90°后得到△A2B2C2,画出旋转后的图形;
(3)借助网格,利用无刻度直尺画出△A1B1C1的中线A1D1.(画图中要体现找关键点的方法)
21.(13分)如图,△ABC的边BC在直线m上,AC⊥BC,且AC=BC,△DEF的边FE也在直线m上,边DF与边AC重合,且DF=EF.
(1)在图①中,请你通过观察、思考,猜想并写出AB与AE所满足的数量关系和位置关系(不要求证明);
(2)当△DEF沿直线m向左平移到图②所示的位置时,DE交AC于点G,连接AE,BG.猜想△BCG与△ACE能否通过旋转重合.请证明你的猜想.
22.(2016山东日照中考)(14分)如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF =BE +DF .
参考答案
1.答案:D
解析:D选项中,只通过平移1号图形得不到2号图形.
2.答案:D
解析:无
3.答案:C
解析:原图形平移后,水平的火柴头应在左边,竖直的火柴头应是一上一下.只有C符合.故选C.
4.答案:D
解析:通过观察可以发现,后一个图形是由前一个图形绕其中心顺时针旋转72°而得到的,故第四个图形应为选项D中的图形.
5.答案:C
解析:将点(-1,2)先向左平移2个单位长度,再向下平移3个单位长度,则平移后得到的点是(-1-2,2-3),即(-3,-1),故选C.
6.答案:D
解析:如图,当OD绕点O旋转至OD'时,OD'∥AC,则∠A+∠AOD'=180°,∴∠AOD'=180°-∠A=100°,∴∠DOD'=∠AOD'-∠AOD=100°-82°=18°,故选D.
7.答案:D
解析:∵∠ABC=90°,将△ABC绕点A顺时针旋转得到△AED,
∴∠CAD=∠CAB,CA=AD,∠B=∠AED=90°,
∴,
∴∠CDE=90°-∠ACD=∠CAD,
∵∠CAD<90°,
∴∠CDE的度数不可能为45°,故选D.
8.答案:B
解析:∵点P(m,m-n)与点Q(-2,3)关于原点对称,∴解得,则不等式组的解集为29.答案:B
解析:由旋转的性质可知BM=BN,
又∵∠MBN=60°,∴△BMN为等边三角形,∴MN=BM,
∵点M是高CH所在直线上的一个动点,∴当BM⊥CH时,BM的长取得最小值,即MN的长取得最小值,此时点M与点H重合.
又∵等边三角形ABC的边长是2,∴AB=BC=CA=2,
∵CH⊥AB,∴BH=AB=1.
∴线段MN长度的最小值是1.故选B.
10.答案:C
解析:∵等边三角形OAB的边长为4,点A在第二象限内,
∴易得点A的坐标为(),B(0,4),
∵平移后点A'的横坐标为6,∠AOB=60°,
∴平移规律为向右平移8个单位,向下平移8个单位,
∴点B'的坐标为(8,-4),故选C.
11.答案:①②③
解析:
12.答案:3
解析:∵三角形ABC沿水平方向向右平移到三角形DEF的位置,
∴AD=BE=CF,
∵BF=BE+EC+CF,∴BE=×(11-5)=3,
∴AD=3.故答案为3.
13.答案:5
解析:∵点P(m-1,5)与点Q(3,2-n)关于原点成中心对称,
∴m-1=-3,2-n=-5,解得m=-2,n=7,则m+n=-2+7=5.
14.答案:平移;A
解析:
15.答案:2
解析:由题意得,1=x-2,y=-2+3,∴x=3,y=1,∴,故答案为2.
16.答案:
解析:在△ABC中,∠ACB=90°,AC=4,BC=3,∴AB=5.∵将△ABC绕点A顺时针旋转,使点B落在AC延长线上点D处,∴AD=AB=5,
∴CD=AD-AC=1,∴S四边形AEDB=.
17.答案:85
解析:由旋转的性质可知,∠BAD=∠CAE=60°,∠C=∠E=65°,
∵AD⊥BC
∴∠CAD=90°-65°=25°,
∴∠BAC=∠BAD+∠CAD=85°,故答案为85.
18.答案:①③
解析:如图,由已知得,∠BAC=90°,
又∠DAE=45°,∴∠1+∠2=45°,
由旋转的性质得,∠2=∠3,AD=AF,
∴∠FAE=∠1+∠3=45°=∠DAE,
又∵AE=AE,
∴△AED≌△AEF,故①正确.
∵AB=AC,∠BAC=90°,
∴∠ABC+∠C=90°,
由旋转的性质知∠4=∠C,
∴∠EBF=∠4+∠ABC=90°,
在Rt△EBF中,BE +BF =EF ,
由△AED≌△AEF,得EF=ED,
由旋转的性质得BF=DC,
∴BE +DC =DE ,故③正确,②不正确.
综上,①③正确.
19.答案:见解析
解析:(1)∵AC=AD,∠CAD=60°,
∴△ACD是等边三角形,
∴DC=AC=4.
(2)过点D作DE⊥BC于点E.
∵△ACD是等边三角形,
∴∠ACD=60°,
又∵AC⊥BC,
∴∠DCE=∠ACB-∠ACD=90°-60°=30°,
∴在Rt△CDE中,DE=DC=2,CE=,
∴BE=BC-CE=.
∴在Rt△BDE中,BD =.
20.答案:见解析
解析:(1)如图,△A1B1C1即为所求作.
(2)如图,△A2B2C2即为所求作.
(3)如图,线段A1D1即为所求作.
21.答案:见解析
解析:(1)AB=AE,AB⊥AE.
(2)将△BCG绕点C顺时针旋转90°后能与△ACE重合.
证明:∵AC⊥BC,DF⊥FE,
∴∠ACB=∠ACE=∠DFE=90°,
又∵DF=EF,∴∠DEF=∠D=45°.
在△CEG中,∵∠ACE=90°,
∴∠CGE=∠GEC=45°.∴CG=CE.
在△BCG和△ACE中,,
∴△BCG≌△ACE(SAS),
∴将△BCG绕点C顺时针旋转90°后能与△ACE重合.
22.答案:见解析
解析:证明:(1)∵将△ADF绕点A顺时针旋转90°后,得到△ABQ,
∴QB=DF,AQ=AF,∠BAQ=∠DAF.
∵∠EAF=45°,∴∠DAF+∠BAE=∠BAQ+∠BAE=45°,
∴∠QAE=45°,∴∠QAE=∠FAE.
在△AQE和△AFE中,,
∴△AQE≌△AFE(SAS),∴∠AEQ=∠AEF,
∴EA是∠QED的平分线.
(2)由(1)得△AQE≌△AFE,∴QE=EF,
由旋转知∠ADF=∠ABQ,
又∠ABD+∠ADF=90°,
∴∠ABD+∠ABQ=90°,即∠QBE=90°.
在Rt△QBE中,QE =BE +QB ,
则EF =BE +DF .
选择题
1.(2019广东揭阳普宁期中)下列四个图案中,不能由1号图形平移得到2号图形的是( )
A.
B.
C.
D.
2.(2017山东泰安中考)如图所示的图案中,为中心对称图形的是( )
A.①②
B.②③
C.②④
D.③④
3.(2020湖北武汉青山期中)四根火柴棒摆成如图所示的象形“口”字,平移此象形字火柴棒后,变成的象形文字是( )
A.
B.
C.
D.
4.观察图中的三个图形,照此规律,可知第四个图形是( )
A.
B.
C.
D.
5.(2020广东佛山顺德期末)在平面直角坐标系中,将点A(-1,2)先向左平移2个单位长度,再向下平移3个单位长度后,得到的点的坐标为( )
A.(1,-1)
B.(-1,5)
C.(-3,-1)
D.(-3,5)
6.如图,∠A=80°,O是AB上一点,直线OD与AB所夹的∠AOD=82°,要使OD∥AC,直线OD绕点O按逆时针方向至少旋转( )
A.8°
B.10°
C.12°
D.18°
7.(2020江苏南京秦淮一模)如图,在△ABC中,∠ABC=90°,将△ABC绕点A顺时针旋转得到△AED使点B的对应点E落在AC上,连接CD,则∠CDE的度数不可能为( )
A.15°
B.20°
C.30°
D.45°
8.(2020独家原创试题)在平面直角坐标系中,若点P(m,m-n)与点Q(-2,3)关于原点对称,则不等式组的正整数解有( )
A.1个
B.2个
C.3个
D.4个
9.如图,等边三角形ABC的边长是2,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接MN,则在点M运动过程中,线段MN长度的最小值是( )
A.
B.1
C.
D.
10.(2020广东佛山高明期末)如图,在平面直角坐标系中,等边三角形OAB的边长为4,点A在第二象限内,将△OAB沿射线AO的方向平移后得到△O'A'B',平移后点A'的横坐标为,则点B'的坐标为( )
A.
B.
C.
D.(8,-4)
填空题
11.如图所示的四组图形中,左边图形与右边图形成中心对称的有__________.(填序号)
12.(2020浙江杭州期末)如图,将三角形ABC沿水平方向向右平移到三角形DEF的位置,若BF=11,EC=5,则A,D之间的距离为__________.
13.(2019湖北天门期未)若点P(m-1,5)与点Q(3,2-n)关于原点成中心对称,则m+n的值是__________.
14.在如图所示的正方形网格中,①经过__________变换(填“平移”“旋转”或“轴对称”)可以得到②;③是由②经过旋转变换得到的,旋转中心是点__________(填“A”“B”或“C”).
15.(2020湖北黄冈蕲春期中)将点A(x,-2)向上平移3个单位,再向左平移2个单位,得到点B(1,y),则=__________.
16.(2017辽宁鞍山中考)如图,在△ABC中,∠ACB=90°,AC=4,BC=3,将△ABC绕点A顺时针旋转得到△ADE(其中点B恰好落在AC延长线上点D处,点C落在点E处),连接BD,则四边形AEDB的面积为_________.
17.(2020四川广元模拟)如图,将△ABC绕点A旋转一定角度后得到△ADE.若∠CAE=60°,∠E=65°,且AD⊥BC,则∠BAC=__________°.
18.如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
①△AED≌△AEF;②BE+DC=DE;③BE +DC =DE ,其中正确的是__________.(填序号)
解答题
19.(10分)如图,已知AC⊥BC,垂足为C,AC=4,BC=,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.
(1)线段DC=___________;
(2)求线段DB的长度.
20.(2020安徽合肥包河一模)(9分)如图,在边长为1的小正方形组成的网格中,给出了格点△ABC(顶点为网格线的交点).
(1)将△ABC先向下平移3个单位长度,再向右平移4个单位长度得到△A1B1C1,画出平移后的图形;
(2)将△ABC绕点A1顺时针旋转90°后得到△A2B2C2,画出旋转后的图形;
(3)借助网格,利用无刻度直尺画出△A1B1C1的中线A1D1.(画图中要体现找关键点的方法)
21.(13分)如图,△ABC的边BC在直线m上,AC⊥BC,且AC=BC,△DEF的边FE也在直线m上,边DF与边AC重合,且DF=EF.
(1)在图①中,请你通过观察、思考,猜想并写出AB与AE所满足的数量关系和位置关系(不要求证明);
(2)当△DEF沿直线m向左平移到图②所示的位置时,DE交AC于点G,连接AE,BG.猜想△BCG与△ACE能否通过旋转重合.请证明你的猜想.
22.(2016山东日照中考)(14分)如图,在正方形ABCD中,E、F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证:
(1)EA是∠QED的平分线;
(2)EF =BE +DF .
参考答案
1.答案:D
解析:D选项中,只通过平移1号图形得不到2号图形.
2.答案:D
解析:无
3.答案:C
解析:原图形平移后,水平的火柴头应在左边,竖直的火柴头应是一上一下.只有C符合.故选C.
4.答案:D
解析:通过观察可以发现,后一个图形是由前一个图形绕其中心顺时针旋转72°而得到的,故第四个图形应为选项D中的图形.
5.答案:C
解析:将点(-1,2)先向左平移2个单位长度,再向下平移3个单位长度,则平移后得到的点是(-1-2,2-3),即(-3,-1),故选C.
6.答案:D
解析:如图,当OD绕点O旋转至OD'时,OD'∥AC,则∠A+∠AOD'=180°,∴∠AOD'=180°-∠A=100°,∴∠DOD'=∠AOD'-∠AOD=100°-82°=18°,故选D.
7.答案:D
解析:∵∠ABC=90°,将△ABC绕点A顺时针旋转得到△AED,
∴∠CAD=∠CAB,CA=AD,∠B=∠AED=90°,
∴,
∴∠CDE=90°-∠ACD=∠CAD,
∵∠CAD<90°,
∴∠CDE的度数不可能为45°,故选D.
8.答案:B
解析:∵点P(m,m-n)与点Q(-2,3)关于原点对称,∴解得,则不等式组的解集为2
解析:由旋转的性质可知BM=BN,
又∵∠MBN=60°,∴△BMN为等边三角形,∴MN=BM,
∵点M是高CH所在直线上的一个动点,∴当BM⊥CH时,BM的长取得最小值,即MN的长取得最小值,此时点M与点H重合.
又∵等边三角形ABC的边长是2,∴AB=BC=CA=2,
∵CH⊥AB,∴BH=AB=1.
∴线段MN长度的最小值是1.故选B.
10.答案:C
解析:∵等边三角形OAB的边长为4,点A在第二象限内,
∴易得点A的坐标为(),B(0,4),
∵平移后点A'的横坐标为6,∠AOB=60°,
∴平移规律为向右平移8个单位,向下平移8个单位,
∴点B'的坐标为(8,-4),故选C.
11.答案:①②③
解析:
12.答案:3
解析:∵三角形ABC沿水平方向向右平移到三角形DEF的位置,
∴AD=BE=CF,
∵BF=BE+EC+CF,∴BE=×(11-5)=3,
∴AD=3.故答案为3.
13.答案:5
解析:∵点P(m-1,5)与点Q(3,2-n)关于原点成中心对称,
∴m-1=-3,2-n=-5,解得m=-2,n=7,则m+n=-2+7=5.
14.答案:平移;A
解析:
15.答案:2
解析:由题意得,1=x-2,y=-2+3,∴x=3,y=1,∴,故答案为2.
16.答案:
解析:在△ABC中,∠ACB=90°,AC=4,BC=3,∴AB=5.∵将△ABC绕点A顺时针旋转,使点B落在AC延长线上点D处,∴AD=AB=5,
∴CD=AD-AC=1,∴S四边形AEDB=.
17.答案:85
解析:由旋转的性质可知,∠BAD=∠CAE=60°,∠C=∠E=65°,
∵AD⊥BC
∴∠CAD=90°-65°=25°,
∴∠BAC=∠BAD+∠CAD=85°,故答案为85.
18.答案:①③
解析:如图,由已知得,∠BAC=90°,
又∠DAE=45°,∴∠1+∠2=45°,
由旋转的性质得,∠2=∠3,AD=AF,
∴∠FAE=∠1+∠3=45°=∠DAE,
又∵AE=AE,
∴△AED≌△AEF,故①正确.
∵AB=AC,∠BAC=90°,
∴∠ABC+∠C=90°,
由旋转的性质知∠4=∠C,
∴∠EBF=∠4+∠ABC=90°,
在Rt△EBF中,BE +BF =EF ,
由△AED≌△AEF,得EF=ED,
由旋转的性质得BF=DC,
∴BE +DC =DE ,故③正确,②不正确.
综上,①③正确.
19.答案:见解析
解析:(1)∵AC=AD,∠CAD=60°,
∴△ACD是等边三角形,
∴DC=AC=4.
(2)过点D作DE⊥BC于点E.
∵△ACD是等边三角形,
∴∠ACD=60°,
又∵AC⊥BC,
∴∠DCE=∠ACB-∠ACD=90°-60°=30°,
∴在Rt△CDE中,DE=DC=2,CE=,
∴BE=BC-CE=.
∴在Rt△BDE中,BD =.
20.答案:见解析
解析:(1)如图,△A1B1C1即为所求作.
(2)如图,△A2B2C2即为所求作.
(3)如图,线段A1D1即为所求作.
21.答案:见解析
解析:(1)AB=AE,AB⊥AE.
(2)将△BCG绕点C顺时针旋转90°后能与△ACE重合.
证明:∵AC⊥BC,DF⊥FE,
∴∠ACB=∠ACE=∠DFE=90°,
又∵DF=EF,∴∠DEF=∠D=45°.
在△CEG中,∵∠ACE=90°,
∴∠CGE=∠GEC=45°.∴CG=CE.
在△BCG和△ACE中,,
∴△BCG≌△ACE(SAS),
∴将△BCG绕点C顺时针旋转90°后能与△ACE重合.
22.答案:见解析
解析:证明:(1)∵将△ADF绕点A顺时针旋转90°后,得到△ABQ,
∴QB=DF,AQ=AF,∠BAQ=∠DAF.
∵∠EAF=45°,∴∠DAF+∠BAE=∠BAQ+∠BAE=45°,
∴∠QAE=45°,∴∠QAE=∠FAE.
在△AQE和△AFE中,,
∴△AQE≌△AFE(SAS),∴∠AEQ=∠AEF,
∴EA是∠QED的平分线.
(2)由(1)得△AQE≌△AFE,∴QE=EF,
由旋转知∠ADF=∠ABQ,
又∠ABD+∠ADF=90°,
∴∠ABD+∠ABQ=90°,即∠QBE=90°.
在Rt△QBE中,QE =BE +QB ,
则EF =BE +DF .
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
