青岛版九年级数学下册 6.6 简单的概率计算第二课时课件(共12张PPT)
文档属性
| 名称 | 青岛版九年级数学下册 6.6 简单的概率计算第二课时课件(共12张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-15 08:03:46 | ||
图片预览




文档简介
(共15张PPT)
6.6 简单的概率计算
第2课时
复习回顾
1、一般地,在一次实验中,如果共有有限个可能发生的结果,并且每种结果发生的可能性都相等,用m表示一个指定事件E包含的结果数,n表示实验可能出现的所有结果的总数,那么事件E发生的概率可用下面的公式计算:
2.三种事件发生的概率及表示?
①必然事件发生的概率为1
记作P(必然事件)=1;
②不可能事件发生的概率为0
记作 P(不可能事件)=0;
③若E为随机事件
则 0<P(A)<1
学习目标
学会使用概率计算公式计算简单随机事件发生的概率.
情境引入
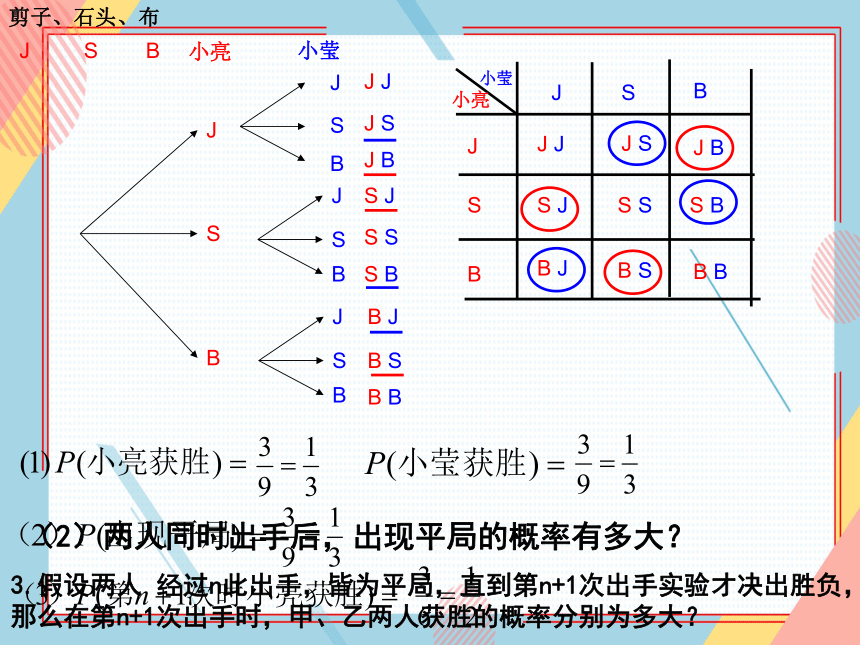
你玩过剪子、石头、布的游戏吗?
小亮和小颖玩这个游戏,游戏规则是:
“剪刀”胜“布”
“布” 胜“石头”
“石头”胜“剪刀”
(1)如果二人都随机出一个手势,那么在第一次“出手”时,小亮获胜的概率有多大?小颖获胜的概率呢?
剪子、石头、布
J S B
J
S
B
小亮
小莹
J
S
B
J
S
B
J
S
B
J J
J S
J B
S J
S S
S B
B J
B S
B B
小亮
小莹
J
S
B
J
S
B
J J
J S
J B
S J
S B
B J
B S
B B
(2)两人同时出手后,出现平局的概率有多大?
3.假设两人 经过n此出手,皆为平局,直到第n+1次出手实验才决出胜负,那么在第n+1次出手时,甲、乙两人获胜的概率分别为多大?
S S
思考
如图,是一个自由转动的转盘,被平均分成六等份,每次转动停止后指针指向偶数的概率是多少?
例3:某快餐店为了招揽顾客,推出一种“转盘”游戏:一个圆形转盘被分成了12个圆心角都相等的扇形,其中有2个扇形涂成红色,4个扇形涂成绿色,其余涂成黄色。顾客消费满200元后,可以自由转动一次转盘。如果转盘停止后,指针落在绿色区域获得二等奖,落在红色区域获得一等奖,凭奖券顾客下次来店就餐时,可分别享受九折、八折优惠。
(1)这个游戏一、二等奖的中奖率分别是多少?
(2)这个游戏的中奖率是多少?
分析:指针落在转盘的位置实际上有无限多个等可能的结果,将转盘等分为若干扇形后,就转化为只有有限多个等可能结果的情况,从而可以利用上节课的公式来计算概率。
从正面分别写有1、2、3、4、5、6的6张卡片中,任意抽出1张,得到下列结果的概率是多少?
(1)卡片上的数字是奇数;
(2)卡片上的数字是偶数;
(3)卡片上的数字不小于3.
跟踪练习
例4:你知道田忌赛马的故事吗?据《史记》记载,在战国时期,齐威王和他的大臣田忌各有上、中、下三匹马,在同等级的马中,齐威王的马比田忌的马跑得快,但每人较高等级的马都比对方较低等级的马跑的快。有一天齐威王要与田忌赛马,双方约定:比赛两局,每局各出一匹,每匹马只赛一次,赢得两局着为胜。齐威王的马按上、中、下顺序出阵,加入田忌的马随机出阵,田忌获胜的概率是多少?
齐:
上
中
下
田:
上
中
下
上
下
中
中
上
下
中
下
上
下
上
中
下
中
上
√
X
X
X
X
X
X
√
X
X
X
√
X
√
√
X
X
√
跟踪练习
一个不透明的口袋中装有红球6个,黄球9个,绿球3个,这些球除颜色外没有任何区别,现从中任意摸出一个球。
(1)计算摸到的是绿球的概率。
(2)如果要使摸到绿球的概率为1/4,需要 在口袋中再放入多少个绿球?
通过今天的学习,你对概率的简单计算有什么收获和新的认识?能谈谈你的想法吗?
本课小结
6.6 简单的概率计算
第2课时
复习回顾
1、一般地,在一次实验中,如果共有有限个可能发生的结果,并且每种结果发生的可能性都相等,用m表示一个指定事件E包含的结果数,n表示实验可能出现的所有结果的总数,那么事件E发生的概率可用下面的公式计算:
2.三种事件发生的概率及表示?
①必然事件发生的概率为1
记作P(必然事件)=1;
②不可能事件发生的概率为0
记作 P(不可能事件)=0;
③若E为随机事件
则 0<P(A)<1
学习目标
学会使用概率计算公式计算简单随机事件发生的概率.
情境引入
你玩过剪子、石头、布的游戏吗?
小亮和小颖玩这个游戏,游戏规则是:
“剪刀”胜“布”
“布” 胜“石头”
“石头”胜“剪刀”
(1)如果二人都随机出一个手势,那么在第一次“出手”时,小亮获胜的概率有多大?小颖获胜的概率呢?
剪子、石头、布
J S B
J
S
B
小亮
小莹
J
S
B
J
S
B
J
S
B
J J
J S
J B
S J
S S
S B
B J
B S
B B
小亮
小莹
J
S
B
J
S
B
J J
J S
J B
S J
S B
B J
B S
B B
(2)两人同时出手后,出现平局的概率有多大?
3.假设两人 经过n此出手,皆为平局,直到第n+1次出手实验才决出胜负,那么在第n+1次出手时,甲、乙两人获胜的概率分别为多大?
S S
思考
如图,是一个自由转动的转盘,被平均分成六等份,每次转动停止后指针指向偶数的概率是多少?
例3:某快餐店为了招揽顾客,推出一种“转盘”游戏:一个圆形转盘被分成了12个圆心角都相等的扇形,其中有2个扇形涂成红色,4个扇形涂成绿色,其余涂成黄色。顾客消费满200元后,可以自由转动一次转盘。如果转盘停止后,指针落在绿色区域获得二等奖,落在红色区域获得一等奖,凭奖券顾客下次来店就餐时,可分别享受九折、八折优惠。
(1)这个游戏一、二等奖的中奖率分别是多少?
(2)这个游戏的中奖率是多少?
分析:指针落在转盘的位置实际上有无限多个等可能的结果,将转盘等分为若干扇形后,就转化为只有有限多个等可能结果的情况,从而可以利用上节课的公式来计算概率。
从正面分别写有1、2、3、4、5、6的6张卡片中,任意抽出1张,得到下列结果的概率是多少?
(1)卡片上的数字是奇数;
(2)卡片上的数字是偶数;
(3)卡片上的数字不小于3.
跟踪练习
例4:你知道田忌赛马的故事吗?据《史记》记载,在战国时期,齐威王和他的大臣田忌各有上、中、下三匹马,在同等级的马中,齐威王的马比田忌的马跑得快,但每人较高等级的马都比对方较低等级的马跑的快。有一天齐威王要与田忌赛马,双方约定:比赛两局,每局各出一匹,每匹马只赛一次,赢得两局着为胜。齐威王的马按上、中、下顺序出阵,加入田忌的马随机出阵,田忌获胜的概率是多少?
齐:
上
中
下
田:
上
中
下
上
下
中
中
上
下
中
下
上
下
上
中
下
中
上
√
X
X
X
X
X
X
√
X
X
X
√
X
√
√
X
X
√
跟踪练习
一个不透明的口袋中装有红球6个,黄球9个,绿球3个,这些球除颜色外没有任何区别,现从中任意摸出一个球。
(1)计算摸到的是绿球的概率。
(2)如果要使摸到绿球的概率为1/4,需要 在口袋中再放入多少个绿球?
通过今天的学习,你对概率的简单计算有什么收获和新的认识?能谈谈你的想法吗?
本课小结
