4.3.2公式法(2) 课件(共27张PPT)
文档属性
| 名称 | 4.3.2公式法(2) 课件(共27张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 654.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-13 21:26:39 | ||
图片预览







文档简介
(共27张PPT)
4.3.2公式法(2)
第四章 因式分解
八年级数学下册同步(北师大版)
学习目标
1.利用完全平方公式的逆向变形对多项式进行因式分解,进一步培养学生的逆向思维能力.
2.掌握完全平方逆向公式的特点,结合提公因式法对复杂多项式进行因式分解.
导入新课
提公因式法:ma+mb+mc=m(a+b+c)
平方差公式法:a2-b2=(a+b)(a-b)
2.练习:
把下列各式分解因式:
① ② x4-16
解:原式=ax2(x2-1)
=ax2(x+1)(x-1).
解:原式=(x2+4)(x2-4)
=(x2 +4)(x+2)(x-2).
1.因式分解学过了哪些方法?
有公因式,先提公因式
因式分解要彻底
导入新课
能把下面4个图形拼成一个正方形并求出你拼成的图形的面积吗?
a
a
b
b
a
b
a
b
ab
a
b
ab
a+b
a+b
a +2ab+b
=
(a+b)2
讲授新课
用完全平方公式分解因式
将完全平方公式倒过来看,得到:
因式分解的完全平方公式
语言叙述:两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
注意:公式中的既可以是单项式,也可以是多项式.
讲授新课
能用完全平方公式分解因式的多项式的特点
我们把a +2ab+b 和a -2ab+b 这样的式子叫做完全平方式.
观察发现:
1.是三项式(或可以看成三项);
2.有两个同号的数或式的平方;
3.中间是这两个数的积的±2倍.
凡具备这些特点的三项式,就是完全平方式.
讲授新课
简记口诀:
首平方,尾平方,首尾两倍在中央.
凡具备这些特点的三项式,就是完全平方式,将它写成完全平方形式,便实现了因式分解.
2
a
b
+b2
±
=(a ± b)
a2
首2
+尾2
±2×首×尾
(首±尾)2
两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
讲授新课
练一练:1.判断下列各式是不是完全平方式.
(1)
(2)
(3)
(4)
(5)
(6)
是
是
不是
不是
是
不是
讲授新课
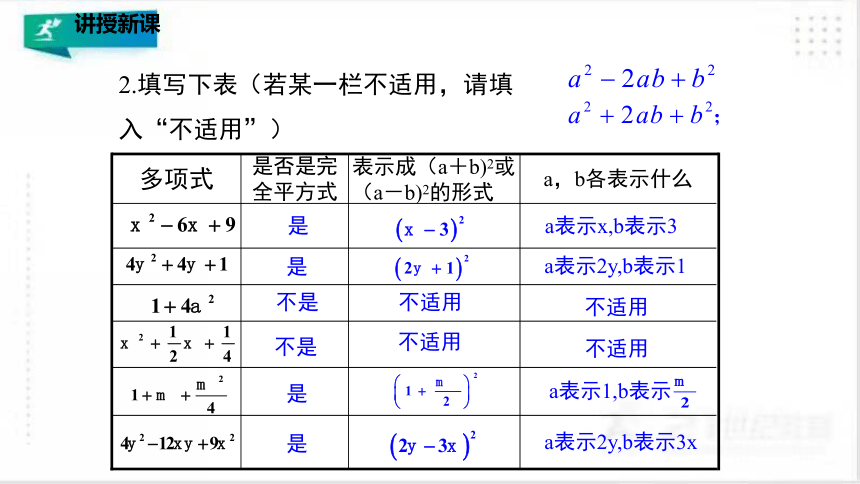
2.填写下表(若某一栏不适用,请填入“不适用”)
a表示x,b表示3
a,b各表示什么
表示成(a+b)2或(a-b)2的形式
是
是否是完全平方式
多项式
是
a表示2y,b表示1
不是
不适用
不适用
不适用
不适用
不是
是
a表示1,b表示
是
a表示2y,b表示3x
讲授新课
例1 把下列完全平方式因式分解:
(1)x2+14x+49; (2) (m+n)2 -6 (m+n)+9.
解:(1)x2+14x+49 = x2+2×7x+72 = (x+7) 2 ;
a2
+
2 a b
+
b2
=
(a+b)2
(2)(m+n)2-6(m+n)+9
=(m+n)2-2·(m+n)·32+32=(m+n-3)2.
a2
-
+
b2
=
(a-b)2
2 a b
讲授新课
例2 把下列各式因式分解:
(1)3ax2+6axy+3ay2;(2)-x2-4y2+4xy.
解:(1)3ax2+6axy+3ay2 = 3a(x2+2xy+y2)=3a(x+y)2;
a2
+
2ab
+
b2
=
(a+b)2
(2)-x2-4y2+4xy= -(x2+4y2-4xy)
= -(x2-4xy+4y2)=-[x2-2·x·2y+(2y)2]= -(x-2y)2.
a2
-
+
b2
=
(a-b)2
2 a b
讲授新课
因式分解的一般步骤:
1、如果多项式的各项含有公因式,那么应先提取公因式;
2、如果多项式的各项不含有公因式,那么可以尝试运用公式法因式分解(即平方差公式和完全平方公式);
3、如果上述方法都不能进行因式分解,那么可以先整理多项式,然后分解;
4、因式分解必须分解到每一个因式都不能再分解为止。
遵循“一提、二套、三检查”的原则
讲授新课
平方差公式 完全平方公式
比较一下:会选择合适的公式进行因式分解
1、有两项
1、有三项
2、两项可写成数或式的平
方形式,且符号相同
2、两项可写成数或式的
平方形式,且符号相
反
3、一项是两数乘积的两倍
十字相乘法公式:
讲授新课
十字相乘法
口诀:(1)因式分解竖直写;
(2)交叉相乘验中项;
(3)横向写出两因式;
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法。
讲授新课
完全平方公式因式分解与十字相乘法的关系:
因式分解:m -6m+9
1
1
-3
-3
-3 +(-3)= -6
解:原式=(m - 3)(m - 3)=(m - 3)2
讲授新课
(1)6=
(2)-6=
(3)12=
(4)-12=
(5)24=
(6)-24=
2×3 或 (-2)×(-3)或1×6或(-1) ×(-6)
1× (-6)或-1×6或2× (-3)或3× (-2)
1× 12或(-1)×(-12)或2× 6或(-2)× (-6) 或3×4 或(-3)× (-4)
1× (-12)或(-1)×12或2×(- 6)或(-2)× 6或3×(-4) 或(-3)× 4
1× 24或(-1)×(-24)或2× 12或(-2)× (-12) 或3×8或(-3)× (-8)或4× 6或(-4)× (-6)
1×(- 24)或(-1)×24或2× (-12)或(-2)× 12或3×(-8)或(-3)× 8或4×(-6)或(-4)× 6
练一练:1.将下面的数表示成两个数的乘积的形式。
讲授新课
因式分解歌
首先提取公因式,其次考虑用公式.
两项考虑平方差,然后立方和与差.三项完全平方式,十字相乘来帮衬.
分组分解试一试,拆项添项功能强.
当堂检测
1. 下列各式中能用完全平方公式进行因式分解的是( )
A.x2+x+1 B.x2+2x-1
C.x2-1 D.x2-6x+9
D
2. 已知x2+16x+k是完全平方式,则常数k等于( )
A.64 B.48
C.32 D.16
A
当堂检测
3. 把多项式(a+b)2-4(a2-b2)+4(a-b)2因式分解的结果为( )
A.(3a-b)2 B.(3b+a)2
C.(3b-a)2 D.(3a+b)2
C
4.把多项式4x2y-4xy2-x3分解因式的结果是( )
A.4xy(x-y)-x3 B.-x(x-2y)2
C.x(4xy-4y2-x2) D.-x(-4xy+4y2+x2)
B
当堂检测
5.对照 a ±2ab+b =(a±b) ,填空:
③.a +4ab+4b =( ) +2· ( ) ·( )+( ) =( )
②.m -6m+9=( ) - 2· ( ) ·( )+( ) =( )
①. x +4x+4= ( ) +2·( )·( )+( ) =( )
x
2
x + 2
a
a 2b
a + 2b
2b
m
m - 3
3
x
2
m
3
当堂检测
6. 若代数式x2+kx+25是一个完全平方式,则k=____.
±10
7. 若一个长方形的面积是x3+2x2+x(x>0),且一边长为x+1,则其邻边长为________.
x2+x
8.若m=2n+1,则m2-4mn+4n2的值是________.
1
9.若关于x的多项式x2-8x+m2是完全平方式,则m的值为___________ .
±4
当堂检测
10. 分解因式:
(1)x2-12x+36; (2)-x2+4xy-4y2;
(3)4(2a+b)2-4(2a+b)+1;(4)y2+2y+1-x2
解:(1)原式 =x2-2·x·6+(6)2
=(x-6)2;
(2)原式 ==-(x2-4xy+4y2)
=-(x-2y)2;
(3)原式=[2(2a+b)] - 2·2(2a+b)·1+(1)
=(4a+2b - 1)2;
(4)原式=(y+1) -x
=(y+1+x)(y+1-x).
当堂检测
11.把下列各式分解因式:
(1)16a4+24a2b2+9b4;(2)-2xy-x2-y2;
(3)4-12(x-y)+9(x-y)2.
解:(1)16a4+24a2b2+9b4
=(4a2)2+2·4a2·3b2+(3b2)2 =(4a2+3b2)2;
(2)-2xy-x2-y2=-(x2+2xy+y2)=-(x+y)2;
(3)4-12(x-y)+9(x-y)2
=22-2×2×3(x-y)+[3(x-y)]2
=[2-3(x-y)]2=(2-3x+3y)2.
当堂检测
12.简便运算:
(1)1002-2×100×99+99 ;(2)342+34×32+162.
解:(1)原式=(100-99) =1
(2)原式=(34+16)2=2500
课堂小结
完全平方公式分解因式
公式
a2±2ab+b2=(a±b)2
特点
(1)要求多项式有三项.
(2)其中两项同号,且都可以写成某数或式的平方,另一项则是这两数或式的乘积的2倍,符号可正可负.
https://www.21cnjy.com/help/help_extract.php
4.3.2公式法(2)
第四章 因式分解
八年级数学下册同步(北师大版)
学习目标
1.利用完全平方公式的逆向变形对多项式进行因式分解,进一步培养学生的逆向思维能力.
2.掌握完全平方逆向公式的特点,结合提公因式法对复杂多项式进行因式分解.
导入新课
提公因式法:ma+mb+mc=m(a+b+c)
平方差公式法:a2-b2=(a+b)(a-b)
2.练习:
把下列各式分解因式:
① ② x4-16
解:原式=ax2(x2-1)
=ax2(x+1)(x-1).
解:原式=(x2+4)(x2-4)
=(x2 +4)(x+2)(x-2).
1.因式分解学过了哪些方法?
有公因式,先提公因式
因式分解要彻底
导入新课
能把下面4个图形拼成一个正方形并求出你拼成的图形的面积吗?
a
a
b
b
a
b
a
b
ab
a
b
ab
a+b
a+b
a +2ab+b
=
(a+b)2
讲授新课
用完全平方公式分解因式
将完全平方公式倒过来看,得到:
因式分解的完全平方公式
语言叙述:两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
注意:公式中的既可以是单项式,也可以是多项式.
讲授新课
能用完全平方公式分解因式的多项式的特点
我们把a +2ab+b 和a -2ab+b 这样的式子叫做完全平方式.
观察发现:
1.是三项式(或可以看成三项);
2.有两个同号的数或式的平方;
3.中间是这两个数的积的±2倍.
凡具备这些特点的三项式,就是完全平方式.
讲授新课
简记口诀:
首平方,尾平方,首尾两倍在中央.
凡具备这些特点的三项式,就是完全平方式,将它写成完全平方形式,便实现了因式分解.
2
a
b
+b2
±
=(a ± b)
a2
首2
+尾2
±2×首×尾
(首±尾)2
两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
讲授新课
练一练:1.判断下列各式是不是完全平方式.
(1)
(2)
(3)
(4)
(5)
(6)
是
是
不是
不是
是
不是
讲授新课
2.填写下表(若某一栏不适用,请填入“不适用”)
a表示x,b表示3
a,b各表示什么
表示成(a+b)2或(a-b)2的形式
是
是否是完全平方式
多项式
是
a表示2y,b表示1
不是
不适用
不适用
不适用
不适用
不是
是
a表示1,b表示
是
a表示2y,b表示3x
讲授新课
例1 把下列完全平方式因式分解:
(1)x2+14x+49; (2) (m+n)2 -6 (m+n)+9.
解:(1)x2+14x+49 = x2+2×7x+72 = (x+7) 2 ;
a2
+
2 a b
+
b2
=
(a+b)2
(2)(m+n)2-6(m+n)+9
=(m+n)2-2·(m+n)·32+32=(m+n-3)2.
a2
-
+
b2
=
(a-b)2
2 a b
讲授新课
例2 把下列各式因式分解:
(1)3ax2+6axy+3ay2;(2)-x2-4y2+4xy.
解:(1)3ax2+6axy+3ay2 = 3a(x2+2xy+y2)=3a(x+y)2;
a2
+
2ab
+
b2
=
(a+b)2
(2)-x2-4y2+4xy= -(x2+4y2-4xy)
= -(x2-4xy+4y2)=-[x2-2·x·2y+(2y)2]= -(x-2y)2.
a2
-
+
b2
=
(a-b)2
2 a b
讲授新课
因式分解的一般步骤:
1、如果多项式的各项含有公因式,那么应先提取公因式;
2、如果多项式的各项不含有公因式,那么可以尝试运用公式法因式分解(即平方差公式和完全平方公式);
3、如果上述方法都不能进行因式分解,那么可以先整理多项式,然后分解;
4、因式分解必须分解到每一个因式都不能再分解为止。
遵循“一提、二套、三检查”的原则
讲授新课
平方差公式 完全平方公式
比较一下:会选择合适的公式进行因式分解
1、有两项
1、有三项
2、两项可写成数或式的平
方形式,且符号相同
2、两项可写成数或式的
平方形式,且符号相
反
3、一项是两数乘积的两倍
十字相乘法公式:
讲授新课
十字相乘法
口诀:(1)因式分解竖直写;
(2)交叉相乘验中项;
(3)横向写出两因式;
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法。
讲授新课
完全平方公式因式分解与十字相乘法的关系:
因式分解:m -6m+9
1
1
-3
-3
-3 +(-3)= -6
解:原式=(m - 3)(m - 3)=(m - 3)2
讲授新课
(1)6=
(2)-6=
(3)12=
(4)-12=
(5)24=
(6)-24=
2×3 或 (-2)×(-3)或1×6或(-1) ×(-6)
1× (-6)或-1×6或2× (-3)或3× (-2)
1× 12或(-1)×(-12)或2× 6或(-2)× (-6) 或3×4 或(-3)× (-4)
1× (-12)或(-1)×12或2×(- 6)或(-2)× 6或3×(-4) 或(-3)× 4
1× 24或(-1)×(-24)或2× 12或(-2)× (-12) 或3×8或(-3)× (-8)或4× 6或(-4)× (-6)
1×(- 24)或(-1)×24或2× (-12)或(-2)× 12或3×(-8)或(-3)× 8或4×(-6)或(-4)× 6
练一练:1.将下面的数表示成两个数的乘积的形式。
讲授新课
因式分解歌
首先提取公因式,其次考虑用公式.
两项考虑平方差,然后立方和与差.三项完全平方式,十字相乘来帮衬.
分组分解试一试,拆项添项功能强.
当堂检测
1. 下列各式中能用完全平方公式进行因式分解的是( )
A.x2+x+1 B.x2+2x-1
C.x2-1 D.x2-6x+9
D
2. 已知x2+16x+k是完全平方式,则常数k等于( )
A.64 B.48
C.32 D.16
A
当堂检测
3. 把多项式(a+b)2-4(a2-b2)+4(a-b)2因式分解的结果为( )
A.(3a-b)2 B.(3b+a)2
C.(3b-a)2 D.(3a+b)2
C
4.把多项式4x2y-4xy2-x3分解因式的结果是( )
A.4xy(x-y)-x3 B.-x(x-2y)2
C.x(4xy-4y2-x2) D.-x(-4xy+4y2+x2)
B
当堂检测
5.对照 a ±2ab+b =(a±b) ,填空:
③.a +4ab+4b =( ) +2· ( ) ·( )+( ) =( )
②.m -6m+9=( ) - 2· ( ) ·( )+( ) =( )
①. x +4x+4= ( ) +2·( )·( )+( ) =( )
x
2
x + 2
a
a 2b
a + 2b
2b
m
m - 3
3
x
2
m
3
当堂检测
6. 若代数式x2+kx+25是一个完全平方式,则k=____.
±10
7. 若一个长方形的面积是x3+2x2+x(x>0),且一边长为x+1,则其邻边长为________.
x2+x
8.若m=2n+1,则m2-4mn+4n2的值是________.
1
9.若关于x的多项式x2-8x+m2是完全平方式,则m的值为___________ .
±4
当堂检测
10. 分解因式:
(1)x2-12x+36; (2)-x2+4xy-4y2;
(3)4(2a+b)2-4(2a+b)+1;(4)y2+2y+1-x2
解:(1)原式 =x2-2·x·6+(6)2
=(x-6)2;
(2)原式 ==-(x2-4xy+4y2)
=-(x-2y)2;
(3)原式=[2(2a+b)] - 2·2(2a+b)·1+(1)
=(4a+2b - 1)2;
(4)原式=(y+1) -x
=(y+1+x)(y+1-x).
当堂检测
11.把下列各式分解因式:
(1)16a4+24a2b2+9b4;(2)-2xy-x2-y2;
(3)4-12(x-y)+9(x-y)2.
解:(1)16a4+24a2b2+9b4
=(4a2)2+2·4a2·3b2+(3b2)2 =(4a2+3b2)2;
(2)-2xy-x2-y2=-(x2+2xy+y2)=-(x+y)2;
(3)4-12(x-y)+9(x-y)2
=22-2×2×3(x-y)+[3(x-y)]2
=[2-3(x-y)]2=(2-3x+3y)2.
当堂检测
12.简便运算:
(1)1002-2×100×99+99 ;(2)342+34×32+162.
解:(1)原式=(100-99) =1
(2)原式=(34+16)2=2500
课堂小结
完全平方公式分解因式
公式
a2±2ab+b2=(a±b)2
特点
(1)要求多项式有三项.
(2)其中两项同号,且都可以写成某数或式的平方,另一项则是这两数或式的乘积的2倍,符号可正可负.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
