人教版高中物理必修二6.3向心力加速度 同步练习提高卷-试卷(word版含答案)
文档属性
| 名称 | 人教版高中物理必修二6.3向心力加速度 同步练习提高卷-试卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-13 21:46:22 | ||
图片预览




文档简介
人教版高中物理必修二6.3向心力加速度 同步练习提高卷
一、单选题(本大题共8道小题)
1. 关于平抛运动和圆周运动,下列说法不正确的是( )
A.平抛运动是匀变速曲线运动
B.做平抛运动的物体在相等时间内速度变化量相同
C.匀速圆周运动是速度不变的运动
D.匀速圆周运动的物体加速度在不断变化
2. 地球上物体由于随地球自转运动而具有向心加速度。对此,下列说法中正确的有( )
A.方向都指向地心 B.赤道处最小
C.两极处最小 D.同一地点质量大的物体向心加速度也大
3. 如图所示,两个摩擦传动的轮子,A为主动轮,已知A、B轮的半径比为R1:R2=1:2,C点离圆心的距离为 ,轮子A和B通过摩擦的传动不打滑,则在两轮子做匀速圆周运动的过程中,以下关于A、B、C三点的线速度大小V、角速度大小ω、向心加速度大小a之间关系的说法正确的是( )
A.VA<VB , ωA=ωB
B.aA>aB , ωB=ωC
C.ωA>ωB , VB=VC
D.ωA<ωB , VB=VC
4. 如图所示,A、B 为小区门口自动升降杆上的两点,A 在杆的顶端,B 在杆的中点处.杆从水平位置匀速转至竖直位置的 过程,下列判断正确的是( )
A.A、B 两点线速度大小之比 1:2
B.A、B 两点角速度大小之比 1:2
C.A、B 两点向心加速度大小之比 1:2
D.A、B 两点向心加速度的方向相同
5. 甲、乙两个物体都做匀速圆周运动,转动半径比为3∶4,在相同的时间里甲转过20圈时,乙转过15圈,则它们所受的向心加速度之比为( )
A.3∶4
B.4∶3
C.4∶9
D.9∶4
6. 小球m用长为L的悬线固定在O点,在O点正下方某处有一光滑圆钉C,今把小球拉到悬线呈水平后无初速地释放,当悬线呈竖直状态且与钉相碰时( )
A.小球的速度突然增大
B.小球的向心加速度突然增大
C.小球的向心加速度不变
D.悬线的拉力突然增大
7. 光滑平面上一运动质点以速度v通过原点O,v与x轴正方向成α角(如图所示),与此同时对质点施加沿x轴正方向的恒力Fx和沿y轴正方向的恒力Fy,则( )
A.质点可能做直线运动 B.质点运动轨迹可能是圆
C.质点运动轨迹可能是抛物线 D.质点一定做匀变速运动
8. 下图为某种自行车的链轮、链条、飞轮、踏板、后轮示意图,在骑行过程中,踏板和链轮同轴转动、飞轮和后轮同轴转动,已知链轮与飞轮的半径之比为3:1,后轮直径为660mm,当脚踩踏板做匀速圆周运动的角速度为5rad/s时,后轮边缘处A点的线速度和向心加速度为( )
A.v=9.90 m/s
B.a=148.50 m/s2
C.v=4.95 m/s
D.a=74.25 m/s2
二、解答题(本大题共3道小题)
9. 运用纳米技术能够制造出超微电机,英国的一家超微研究所宣称其制造的超微电机转子的半径只有30μm,转速高达2000r/min,试估算位于转子边缘的一个质量为10 × 10 - 26kg的原子的向心加速度大小。(保留两位有效数字)
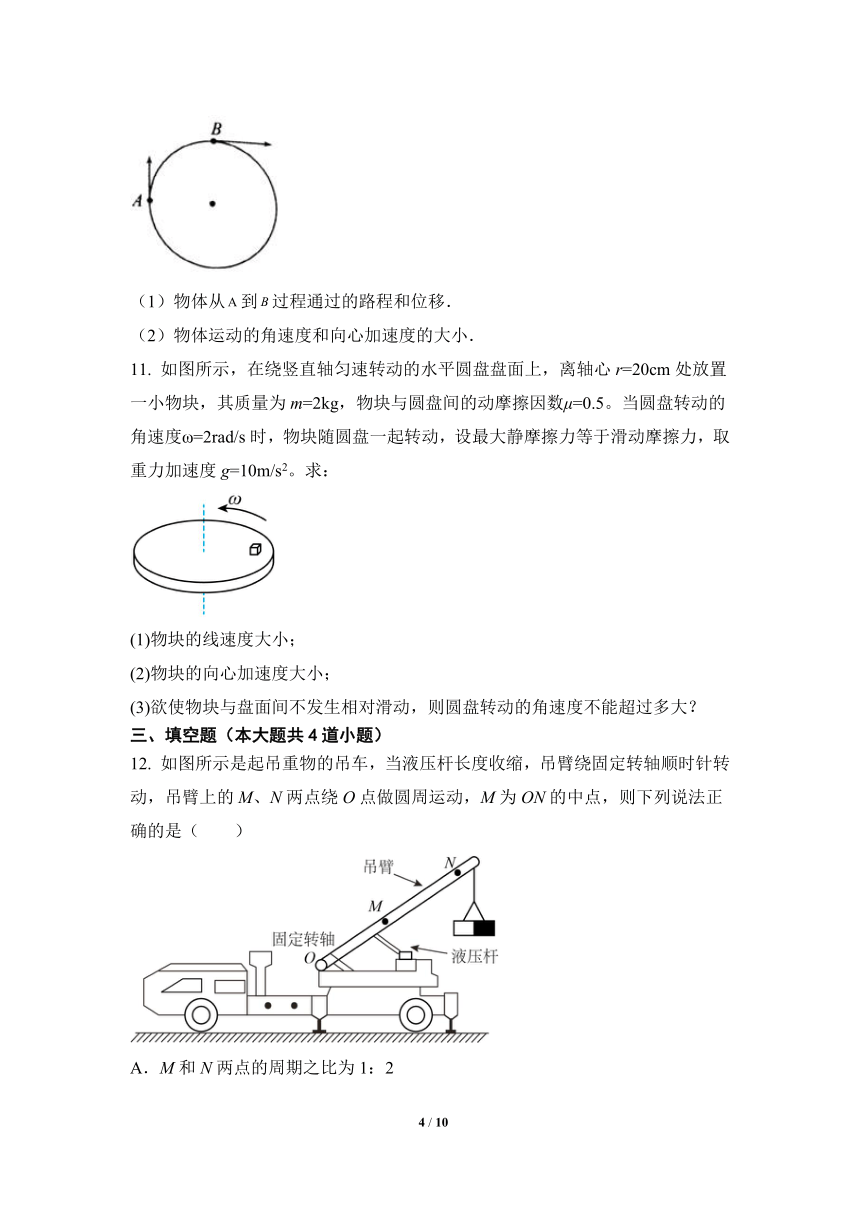
10. 一物体沿半径为的圆形轨道在水平面内做匀速圆周运动,线速度为,在点运动方向为正北,经周期运动至点,在点运动方向为正东,如图所示,求:
(1)物体从到过程通过的路程和位移.
(2)物体运动的角速度和向心加速度的大小.
11. 如图所示,在绕竖直轴匀速转动的水平圆盘盘面上,离轴心r=20cm处放置一小物块,其质量为m=2kg,物块与圆盘间的动摩擦因数μ=0.5。当圆盘转动的角速度ω=2rad/s时,物块随圆盘一起转动,设最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2。求:
(1)物块的线速度大小;
(2)物块的向心加速度大小;
(3)欲使物块与盘面间不发生相对滑动,则圆盘转动的角速度不能超过多大?
三、填空题(本大题共4道小题)
12. 如图所示是起吊重物的吊车,当液压杆长度收缩,吊臂绕固定转轴顺时针转动,吊臂上的M、N两点绕O点做圆周运动,M为ON的中点,则下列说法正确的是( )
A.M和N两点的周期之比为1:2
B.M和N两点的角速度之比为1:2
C.M和N两点的线速度之比为1:2
D.M和N两点的向心加速度之比为1:4
13. 小明骑着一辆自行车(甲图)在平直的路面上匀速前行,脚踏板连接的大齿轮与后轮上的小齿轮通过链条传动,可将大齿轮、小齿轮、后轮简化为如图乙所示模型,A、B、C分别为大齿轮、小齿轮、后轮边缘上的一质点,则角速度ωA______ωB(填“>”、“=”或“<”),向心加速度aB______aC(填“>”、“=”或“<”).
14. 如图所示,摩擦轮A和B通过中介轮C进行传动,A为主动轮,B、C为从动轮,A的半径为20cm,B的半径为10cm,C的半径为15cm,则A、B两轮边缘上的点的线速度大小之比vA:vB=_____,角速度之比ωA:ωB=_____,向心加速度之比aA:aB=_____。
15. 半径50m的摩天轮匀速转动,周期为1200s。座舱经过底部弧长5m的范围为下客区域,则舱内乘客有______s时间出舱。若乘客能感受到的最小加速度约0.02m/s2,则乘客在乘坐该摩天轮时______(选填“能”或“不能”)感受到因转动而产生的加速度。
答案
一、单选题(本大题共8道小题)
1. 【答案】C
【详解】
AB.平抛运动的加速度为重力加速度,所以加速度恒定不变,则在相等的时间内速度的改变量一定相等,是匀变速曲线运动,故AB不符题意;
C.匀速圆周运动的线速度大小不变,而线速度的方向改变,则其速度改变,是变速运动,故C符合题意;
D.匀速圆周运动的加速度就是向心加速度,始终指向圆心,故方向时刻改变,故D不符题意;
故选C。
2. 【答案】C
【详解】
向心加速度指向做圆周运动的圆心,随地球自转的物体的向心加速度指向所在纬线的圆的圆心,轨道半径在赤道上最大,两极处最小,由a=ω2r知,向心加速度在赤道处最大,两极处最小,与质量无关。
故选C。
3. 【答案】B
【详解】
A.因为靠摩擦传动轮子边缘上点的线速度大小相等,所以vA=vB,R1:R2=1:2,根据v=rω知,ωA:ωB=2:1,故A错误;
B.A、B两点的线速度大小相等,根据a=v2/r知,aA>aB.B、C共轴转动,则角速度相等.故B正确.
CD.A、B两点的线速度大小相等,根据v=rω知,ωA>ωB;B、C的角速度相等,根据v=rω知,vB>vC,故CD错误;
故选B.
4. 【答案】D
【详解】
A、B两点在同一根杆上角速度相等,故B错误;根据v=ωr,可知vA:vB=rA:rB=2:1,故A错误;根据可知,aA:aB=rA:rB=2:1,故C错误;A、B 两点向心加速度的方向均指向圆心,故D正确.所以D正确,ABC错误.
5. 【答案】B
【解析】
【详解】
相同时间里甲转过20圈,乙转过15圈,根据角速度定义可知
由题意可知
根据得它们所受的向心加速度之比为
故B正确,A、C、D错误;
故选B。
6. 【答案】BD
【解析】
【详解】
A.在最低点小球受到重力和绳子的拉力作用,且两个力与小球的运动方向都垂直,则这两个力都不做功,所以悬线与钉子碰撞的前后瞬间,小球的线速度大小不变.故A错误;
BC.根据随着半径的减小,向心加速度增大,故B正确;C错误;
D.根据牛顿第二定律可知半径减小,则绳子的拉力F增大,故D正确;
7. 【答案】ACD
【详解】
AC.由于Fx和Fy均为恒力,其合力F也为恒力,当F的方向与v的方向相同时,质点做匀加速直线运动,当F的方向与v的方向垂直时,质点做类平抛运动,轨迹为抛物线,AC正确;
B.恒力作用下质点运动的加速度恒定,一定做匀变速运动,不可能做圆周运动,故运动轨迹不可能是圆,B错误,D正确。
故选ACD。
8. 【答案】CD
【详解】
A、C、踏板与链轮同轴转动,角速度相等,飞轮与后轮同轴转动,角速度相等.而链轮和飞轮用链条连接,线速度相等,所以可知飞轮的角速度为踏板角速度的3倍,即为15rad/s,根据v=rω,则后轮的线速度为v=4.95 m/s,故A错误,C正确.B、D、向心加速度为a=vω=4.95m/s×15 rad/s=74.25 m/s,则B错误,选项D正确.故选CD.
二、解答题(本大题共3道小题)
9. 【答案】1.3m/s2
【详解】
周期
T = = s = 0.03s
原子的角速度
ω = = rad/s
原子的向心加速度
a = ω2r = × 30 × 10 - 6m/s2 ≈ 1.3m/s2
10. 【答案】(1)从A到B的路程为: ,位移为:,方向由A指向B ;
(2)物体运动的角速度和向心加速度的大小分别为, .
【解析】
【详解】
(1)物体从A到B的过程中路程为:
物体从A到B的过程中位移大小为:
方向由A指向B.
(2)角速度为:
向心加速度为:
答案:(1) ,方向由A指向B.(2)物体运动的角速度,向心加速度的大小.
11. 【答案】(1)0.4 m/s (2)0.8 m/s2 (3)5 rad/s
【详解】
(1)当时,滑块的线速度
(2)当时,滑块的向心加速度
(3)当物块刚要发生滑动时最大静摩擦力充当向心力,设此时圆盘转动的角速度为
由牛顿第二定律得
解得
故圆盘转动的角速度不能超过。
三、填空题(本大题共4道小题)
12. 【答案】C
【详解】
A.因为吊臂上的M、N两点绕O点做圆周运动,可知M和N两点的周期之比为1:1,A错误;
B.因为吊臂上的M、N两点绕O点做圆周运动,可知M和N两点的角速度之比为1:1,B错误;
C.因为吊臂上的M、N两点绕O点做圆周运动,M为ON的中点,由可知M和N两点的线速度之比为1:2,C正确;
D.因为吊臂上的M、N两点绕O点做圆周运动,M为ON的中点,由可知M和N两点的加速度之比为1:2,D错误。
故选C。
13. 【答案】 < ; <
【解析】
【详解】
A、B两点靠链条传动,线速度相等,根据v=rω知,A、B两点角速度与半径成反比,rA>rB,故ωA<ωB ;B、C两点具有相等的角速度,由向心加速度a=ω2R知,B、C向心加速度与半径成正比,rB<rC.故aB<aC.
14. 【答案】 1:1 1:2 1:2
【详解】
摩擦轮A和B通过中介轮C进行传动,三个轮子边缘上的点线速度大小相等
vA:vB=1:1
A、B两轮边缘上的点半径之比为2:1,根据v=ωr可得,角速度之比为1:2。
A、B两轮边缘上的点半径之比为2:1,根据知,则向心加速度之比为1:2。
15. 【答案】 19.1 不能
【详解】
摩天轮边缘的线速度为
舱内乘客能出舱的时间为
摩天轮边缘的向心加速度大小为
则乘客在乘坐该摩天轮时不能感受到因转动而产生的加速度。
2 / 2
一、单选题(本大题共8道小题)
1. 关于平抛运动和圆周运动,下列说法不正确的是( )
A.平抛运动是匀变速曲线运动
B.做平抛运动的物体在相等时间内速度变化量相同
C.匀速圆周运动是速度不变的运动
D.匀速圆周运动的物体加速度在不断变化
2. 地球上物体由于随地球自转运动而具有向心加速度。对此,下列说法中正确的有( )
A.方向都指向地心 B.赤道处最小
C.两极处最小 D.同一地点质量大的物体向心加速度也大
3. 如图所示,两个摩擦传动的轮子,A为主动轮,已知A、B轮的半径比为R1:R2=1:2,C点离圆心的距离为 ,轮子A和B通过摩擦的传动不打滑,则在两轮子做匀速圆周运动的过程中,以下关于A、B、C三点的线速度大小V、角速度大小ω、向心加速度大小a之间关系的说法正确的是( )
A.VA<VB , ωA=ωB
B.aA>aB , ωB=ωC
C.ωA>ωB , VB=VC
D.ωA<ωB , VB=VC
4. 如图所示,A、B 为小区门口自动升降杆上的两点,A 在杆的顶端,B 在杆的中点处.杆从水平位置匀速转至竖直位置的 过程,下列判断正确的是( )
A.A、B 两点线速度大小之比 1:2
B.A、B 两点角速度大小之比 1:2
C.A、B 两点向心加速度大小之比 1:2
D.A、B 两点向心加速度的方向相同
5. 甲、乙两个物体都做匀速圆周运动,转动半径比为3∶4,在相同的时间里甲转过20圈时,乙转过15圈,则它们所受的向心加速度之比为( )
A.3∶4
B.4∶3
C.4∶9
D.9∶4
6. 小球m用长为L的悬线固定在O点,在O点正下方某处有一光滑圆钉C,今把小球拉到悬线呈水平后无初速地释放,当悬线呈竖直状态且与钉相碰时( )
A.小球的速度突然增大
B.小球的向心加速度突然增大
C.小球的向心加速度不变
D.悬线的拉力突然增大
7. 光滑平面上一运动质点以速度v通过原点O,v与x轴正方向成α角(如图所示),与此同时对质点施加沿x轴正方向的恒力Fx和沿y轴正方向的恒力Fy,则( )
A.质点可能做直线运动 B.质点运动轨迹可能是圆
C.质点运动轨迹可能是抛物线 D.质点一定做匀变速运动
8. 下图为某种自行车的链轮、链条、飞轮、踏板、后轮示意图,在骑行过程中,踏板和链轮同轴转动、飞轮和后轮同轴转动,已知链轮与飞轮的半径之比为3:1,后轮直径为660mm,当脚踩踏板做匀速圆周运动的角速度为5rad/s时,后轮边缘处A点的线速度和向心加速度为( )
A.v=9.90 m/s
B.a=148.50 m/s2
C.v=4.95 m/s
D.a=74.25 m/s2
二、解答题(本大题共3道小题)
9. 运用纳米技术能够制造出超微电机,英国的一家超微研究所宣称其制造的超微电机转子的半径只有30μm,转速高达2000r/min,试估算位于转子边缘的一个质量为10 × 10 - 26kg的原子的向心加速度大小。(保留两位有效数字)
10. 一物体沿半径为的圆形轨道在水平面内做匀速圆周运动,线速度为,在点运动方向为正北,经周期运动至点,在点运动方向为正东,如图所示,求:
(1)物体从到过程通过的路程和位移.
(2)物体运动的角速度和向心加速度的大小.
11. 如图所示,在绕竖直轴匀速转动的水平圆盘盘面上,离轴心r=20cm处放置一小物块,其质量为m=2kg,物块与圆盘间的动摩擦因数μ=0.5。当圆盘转动的角速度ω=2rad/s时,物块随圆盘一起转动,设最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2。求:
(1)物块的线速度大小;
(2)物块的向心加速度大小;
(3)欲使物块与盘面间不发生相对滑动,则圆盘转动的角速度不能超过多大?
三、填空题(本大题共4道小题)
12. 如图所示是起吊重物的吊车,当液压杆长度收缩,吊臂绕固定转轴顺时针转动,吊臂上的M、N两点绕O点做圆周运动,M为ON的中点,则下列说法正确的是( )
A.M和N两点的周期之比为1:2
B.M和N两点的角速度之比为1:2
C.M和N两点的线速度之比为1:2
D.M和N两点的向心加速度之比为1:4
13. 小明骑着一辆自行车(甲图)在平直的路面上匀速前行,脚踏板连接的大齿轮与后轮上的小齿轮通过链条传动,可将大齿轮、小齿轮、后轮简化为如图乙所示模型,A、B、C分别为大齿轮、小齿轮、后轮边缘上的一质点,则角速度ωA______ωB(填“>”、“=”或“<”),向心加速度aB______aC(填“>”、“=”或“<”).
14. 如图所示,摩擦轮A和B通过中介轮C进行传动,A为主动轮,B、C为从动轮,A的半径为20cm,B的半径为10cm,C的半径为15cm,则A、B两轮边缘上的点的线速度大小之比vA:vB=_____,角速度之比ωA:ωB=_____,向心加速度之比aA:aB=_____。
15. 半径50m的摩天轮匀速转动,周期为1200s。座舱经过底部弧长5m的范围为下客区域,则舱内乘客有______s时间出舱。若乘客能感受到的最小加速度约0.02m/s2,则乘客在乘坐该摩天轮时______(选填“能”或“不能”)感受到因转动而产生的加速度。
答案
一、单选题(本大题共8道小题)
1. 【答案】C
【详解】
AB.平抛运动的加速度为重力加速度,所以加速度恒定不变,则在相等的时间内速度的改变量一定相等,是匀变速曲线运动,故AB不符题意;
C.匀速圆周运动的线速度大小不变,而线速度的方向改变,则其速度改变,是变速运动,故C符合题意;
D.匀速圆周运动的加速度就是向心加速度,始终指向圆心,故方向时刻改变,故D不符题意;
故选C。
2. 【答案】C
【详解】
向心加速度指向做圆周运动的圆心,随地球自转的物体的向心加速度指向所在纬线的圆的圆心,轨道半径在赤道上最大,两极处最小,由a=ω2r知,向心加速度在赤道处最大,两极处最小,与质量无关。
故选C。
3. 【答案】B
【详解】
A.因为靠摩擦传动轮子边缘上点的线速度大小相等,所以vA=vB,R1:R2=1:2,根据v=rω知,ωA:ωB=2:1,故A错误;
B.A、B两点的线速度大小相等,根据a=v2/r知,aA>aB.B、C共轴转动,则角速度相等.故B正确.
CD.A、B两点的线速度大小相等,根据v=rω知,ωA>ωB;B、C的角速度相等,根据v=rω知,vB>vC,故CD错误;
故选B.
4. 【答案】D
【详解】
A、B两点在同一根杆上角速度相等,故B错误;根据v=ωr,可知vA:vB=rA:rB=2:1,故A错误;根据可知,aA:aB=rA:rB=2:1,故C错误;A、B 两点向心加速度的方向均指向圆心,故D正确.所以D正确,ABC错误.
5. 【答案】B
【解析】
【详解】
相同时间里甲转过20圈,乙转过15圈,根据角速度定义可知
由题意可知
根据得它们所受的向心加速度之比为
故B正确,A、C、D错误;
故选B。
6. 【答案】BD
【解析】
【详解】
A.在最低点小球受到重力和绳子的拉力作用,且两个力与小球的运动方向都垂直,则这两个力都不做功,所以悬线与钉子碰撞的前后瞬间,小球的线速度大小不变.故A错误;
BC.根据随着半径的减小,向心加速度增大,故B正确;C错误;
D.根据牛顿第二定律可知半径减小,则绳子的拉力F增大,故D正确;
7. 【答案】ACD
【详解】
AC.由于Fx和Fy均为恒力,其合力F也为恒力,当F的方向与v的方向相同时,质点做匀加速直线运动,当F的方向与v的方向垂直时,质点做类平抛运动,轨迹为抛物线,AC正确;
B.恒力作用下质点运动的加速度恒定,一定做匀变速运动,不可能做圆周运动,故运动轨迹不可能是圆,B错误,D正确。
故选ACD。
8. 【答案】CD
【详解】
A、C、踏板与链轮同轴转动,角速度相等,飞轮与后轮同轴转动,角速度相等.而链轮和飞轮用链条连接,线速度相等,所以可知飞轮的角速度为踏板角速度的3倍,即为15rad/s,根据v=rω,则后轮的线速度为v=4.95 m/s,故A错误,C正确.B、D、向心加速度为a=vω=4.95m/s×15 rad/s=74.25 m/s,则B错误,选项D正确.故选CD.
二、解答题(本大题共3道小题)
9. 【答案】1.3m/s2
【详解】
周期
T = = s = 0.03s
原子的角速度
ω = = rad/s
原子的向心加速度
a = ω2r = × 30 × 10 - 6m/s2 ≈ 1.3m/s2
10. 【答案】(1)从A到B的路程为: ,位移为:,方向由A指向B ;
(2)物体运动的角速度和向心加速度的大小分别为, .
【解析】
【详解】
(1)物体从A到B的过程中路程为:
物体从A到B的过程中位移大小为:
方向由A指向B.
(2)角速度为:
向心加速度为:
答案:(1) ,方向由A指向B.(2)物体运动的角速度,向心加速度的大小.
11. 【答案】(1)0.4 m/s (2)0.8 m/s2 (3)5 rad/s
【详解】
(1)当时,滑块的线速度
(2)当时,滑块的向心加速度
(3)当物块刚要发生滑动时最大静摩擦力充当向心力,设此时圆盘转动的角速度为
由牛顿第二定律得
解得
故圆盘转动的角速度不能超过。
三、填空题(本大题共4道小题)
12. 【答案】C
【详解】
A.因为吊臂上的M、N两点绕O点做圆周运动,可知M和N两点的周期之比为1:1,A错误;
B.因为吊臂上的M、N两点绕O点做圆周运动,可知M和N两点的角速度之比为1:1,B错误;
C.因为吊臂上的M、N两点绕O点做圆周运动,M为ON的中点,由可知M和N两点的线速度之比为1:2,C正确;
D.因为吊臂上的M、N两点绕O点做圆周运动,M为ON的中点,由可知M和N两点的加速度之比为1:2,D错误。
故选C。
13. 【答案】 < ; <
【解析】
【详解】
A、B两点靠链条传动,线速度相等,根据v=rω知,A、B两点角速度与半径成反比,rA>rB,故ωA<ωB ;B、C两点具有相等的角速度,由向心加速度a=ω2R知,B、C向心加速度与半径成正比,rB<rC.故aB<aC.
14. 【答案】 1:1 1:2 1:2
【详解】
摩擦轮A和B通过中介轮C进行传动,三个轮子边缘上的点线速度大小相等
vA:vB=1:1
A、B两轮边缘上的点半径之比为2:1,根据v=ωr可得,角速度之比为1:2。
A、B两轮边缘上的点半径之比为2:1,根据知,则向心加速度之比为1:2。
15. 【答案】 19.1 不能
【详解】
摩天轮边缘的线速度为
舱内乘客能出舱的时间为
摩天轮边缘的向心加速度大小为
则乘客在乘坐该摩天轮时不能感受到因转动而产生的加速度。
2 / 2
