八年级数学(下)学案案(第十一章)11.4三角形内角和定理(第1课时)
文档属性
| 名称 | 八年级数学(下)学案案(第十一章)11.4三角形内角和定理(第1课时) |  | |
| 格式 | zip | ||
| 文件大小 | 45.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-20 22:45:50 | ||
图片预览

文档简介
八年级数学(下)学案案(第十一章)
11.4三角形内角和定理(第1课时)
【学习目标】1.掌握“三角形内角和定理”的证明及简单应用;
2.通过猜想、推理等数学活动,感受数学活动充满着探索以及数学结论的确定性,提高学生的学习数学的兴趣。
重点:三角形内角和定理及其推论的证明和应用。
【课前预习】
预习内容:自学教科书P126-127上面的内容,完成下列问题:
你有哪些方法求三角形的内角和,下面的方法是怎么做的?
用度量的方法可以发现三角形的内角和是 ______度;
折叠三角形的三个内角拼到一起,拼成一个______角:
如图:先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行,然后把另外两角相向对折,
使其顶点与已折角的顶点相嵌合(图(2)、(3)),最后得图(4)所示的结果.
将纸片三角形三顶角剪下,随意将它们拼凑在一起.
由实验可知:三角形的内角之和正好为一个______角.
归纳总结:三角形内角和定理: 。
推论1: 。
推论2: 。
练习:已知:如图,四边形ABCD是一个任意四边形。
求证:∠A+∠B+∠C+∠D=360°
【课中导学】
问题一:什么是三角形内角和定理?它的两个推论是什么?
问题二:完成下列填空:
1.证明“三角形内角和定理”
已知:ABC的三个内角是∠A,∠B,∠C
求证:∠A+∠B+∠ACB=180°
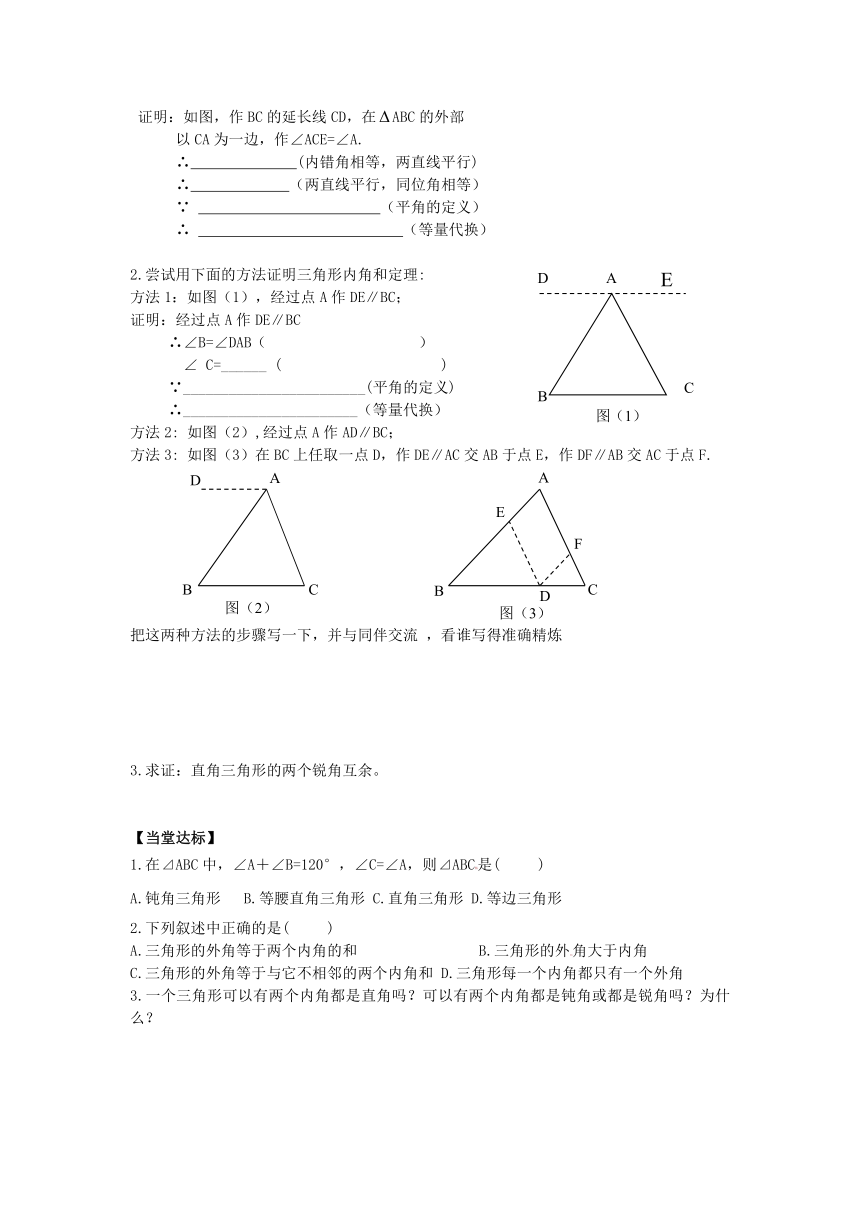
证明:如图,作BC的延长线CD,在ABC的外部
以CA为一边,作∠ACE=∠A.
∴ (内错角相等,两直线平行)
∴ (两直线平行,同位角相等)
∵ (平角的定义)
∴ (等量代换)
2.尝试用下面的方法证明三角形内角和定理:
方法1:如图(1),经过点A作DE∥BC;
证明:经过点A作DE∥BC
∴∠B=∠DAB( )
∠ C=______ ( )
∵________________________(平角的定义)
∴_______________________(等量代换)
方法2: 如图(2),经过点A作AD∥BC;
方法3: 如图(3)在BC上任取一点D,作DE∥AC交AB于点E,作DF∥AB交AC于点F.
把这两种方法的步骤写一下,并与同伴交流 ,看谁写得准确精炼
3.求证:直角三角形的两个锐角互余。
【当堂达标】
1.在⊿ABC中,∠A+∠B=120°,∠C=∠A,则⊿ABC是(?? ) A.钝角三角形? B.等腰直角三角形 C.直角三角形 D.等边三角形
2.下列叙述中正确的是(?? ) A.三角形的外角等于两个内角的和????? B.三角形的外角大于内角 C.三角形的外角等于与它不相邻的两个内角和 D.三角形每一个内角都只有一个外角
3.一个三角形可以有两个内角都是直角吗?可以有两个内角都是钝角或都是锐角吗?为什么?
4.填空:在△ABC中,
(1)∠A=80°,∠B=60°,则∠C=______;
(2)∠A=40°,∠B=∠C,则∠B=_______;
(3)∠A=∠B=∠C,则∠B=_______;
(4)∠C=4∠A,∠A+∠B=100°,则∠A=_______;与∠C相邻的外角=_______.
5.求证:有两角互余的三角形是直角三角形。
已知:
求证:
证明:
6.已知:如图,在△ABC中,∠DAC=∠B
求证:∠ADC=∠BAC
【巩固训练】
一、选择题
1.一个三角形三内角之比为1:2:3,则此三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法判断
2.一个等腰三角形中有一个角是60°,则这个等腰三角形的另两个内角是( )
A.60°,60° B.60°,90° C.90°,30° D.100°,60°
3.下列说法正确的是( )
A.在一个三角形中,最小的一个角是65°
B.在一个三角形中,最大的一个角是47°
C.在一个三角形中,三个内角可以都是钝角
D.在一个三角形中,三个内角可以都是锐角
4.已知:如图,则∠A等于( )
A.60° B.70°
C.50° D.80° 4题图
5.已知,如图ABC中,∠B=∠DAC,则∠BAC
和∠ADC的关系是( )
A.∠BAC<∠ADC B.∠BAC=∠ADC
C.∠BAC>∠ADC D.不能确定
6.在ABC中,已知∠A+∠C=2∠B,
∠C-∠A=80°,则∠C的度数是( ) 5题图
A.60° B.80° C.100° D.120°
二、填空
1.ABC中,∠A=∠B=∠C,
则∠A= ,∠B= ,∠C= 。
2.如图,∠A+∠B+∠C+∠D+∠E+∠F= 。
三、解答题
已知:如图ABC中,∠B=∠C= 30°,AD⊥AC于点
A,求∠BAD的度数。
11.4三角形内角和定理(第1课时)
【学习目标】1.掌握“三角形内角和定理”的证明及简单应用;
2.通过猜想、推理等数学活动,感受数学活动充满着探索以及数学结论的确定性,提高学生的学习数学的兴趣。
重点:三角形内角和定理及其推论的证明和应用。
【课前预习】
预习内容:自学教科书P126-127上面的内容,完成下列问题:
你有哪些方法求三角形的内角和,下面的方法是怎么做的?
用度量的方法可以发现三角形的内角和是 ______度;
折叠三角形的三个内角拼到一起,拼成一个______角:
如图:先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行,然后把另外两角相向对折,
使其顶点与已折角的顶点相嵌合(图(2)、(3)),最后得图(4)所示的结果.
将纸片三角形三顶角剪下,随意将它们拼凑在一起.
由实验可知:三角形的内角之和正好为一个______角.
归纳总结:三角形内角和定理: 。
推论1: 。
推论2: 。
练习:已知:如图,四边形ABCD是一个任意四边形。
求证:∠A+∠B+∠C+∠D=360°
【课中导学】
问题一:什么是三角形内角和定理?它的两个推论是什么?
问题二:完成下列填空:
1.证明“三角形内角和定理”
已知:ABC的三个内角是∠A,∠B,∠C
求证:∠A+∠B+∠ACB=180°
证明:如图,作BC的延长线CD,在ABC的外部
以CA为一边,作∠ACE=∠A.
∴ (内错角相等,两直线平行)
∴ (两直线平行,同位角相等)
∵ (平角的定义)
∴ (等量代换)
2.尝试用下面的方法证明三角形内角和定理:
方法1:如图(1),经过点A作DE∥BC;
证明:经过点A作DE∥BC
∴∠B=∠DAB( )
∠ C=______ ( )
∵________________________(平角的定义)
∴_______________________(等量代换)
方法2: 如图(2),经过点A作AD∥BC;
方法3: 如图(3)在BC上任取一点D,作DE∥AC交AB于点E,作DF∥AB交AC于点F.
把这两种方法的步骤写一下,并与同伴交流 ,看谁写得准确精炼
3.求证:直角三角形的两个锐角互余。
【当堂达标】
1.在⊿ABC中,∠A+∠B=120°,∠C=∠A,则⊿ABC是(?? ) A.钝角三角形? B.等腰直角三角形 C.直角三角形 D.等边三角形
2.下列叙述中正确的是(?? ) A.三角形的外角等于两个内角的和????? B.三角形的外角大于内角 C.三角形的外角等于与它不相邻的两个内角和 D.三角形每一个内角都只有一个外角
3.一个三角形可以有两个内角都是直角吗?可以有两个内角都是钝角或都是锐角吗?为什么?
4.填空:在△ABC中,
(1)∠A=80°,∠B=60°,则∠C=______;
(2)∠A=40°,∠B=∠C,则∠B=_______;
(3)∠A=∠B=∠C,则∠B=_______;
(4)∠C=4∠A,∠A+∠B=100°,则∠A=_______;与∠C相邻的外角=_______.
5.求证:有两角互余的三角形是直角三角形。
已知:
求证:
证明:
6.已知:如图,在△ABC中,∠DAC=∠B
求证:∠ADC=∠BAC
【巩固训练】
一、选择题
1.一个三角形三内角之比为1:2:3,则此三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法判断
2.一个等腰三角形中有一个角是60°,则这个等腰三角形的另两个内角是( )
A.60°,60° B.60°,90° C.90°,30° D.100°,60°
3.下列说法正确的是( )
A.在一个三角形中,最小的一个角是65°
B.在一个三角形中,最大的一个角是47°
C.在一个三角形中,三个内角可以都是钝角
D.在一个三角形中,三个内角可以都是锐角
4.已知:如图,则∠A等于( )
A.60° B.70°
C.50° D.80° 4题图
5.已知,如图ABC中,∠B=∠DAC,则∠BAC
和∠ADC的关系是( )
A.∠BAC<∠ADC B.∠BAC=∠ADC
C.∠BAC>∠ADC D.不能确定
6.在ABC中,已知∠A+∠C=2∠B,
∠C-∠A=80°,则∠C的度数是( ) 5题图
A.60° B.80° C.100° D.120°
二、填空
1.ABC中,∠A=∠B=∠C,
则∠A= ,∠B= ,∠C= 。
2.如图,∠A+∠B+∠C+∠D+∠E+∠F= 。
三、解答题
已知:如图ABC中,∠B=∠C= 30°,AD⊥AC于点
A,求∠BAD的度数。
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
