八年级数学(下)学案案(第十一章)11.4三角形内角和定理(第2课时)
文档属性
| 名称 | 八年级数学(下)学案案(第十一章)11.4三角形内角和定理(第2课时) |  | |
| 格式 | zip | ||
| 文件大小 | 38.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-20 22:55:11 | ||
图片预览

文档简介
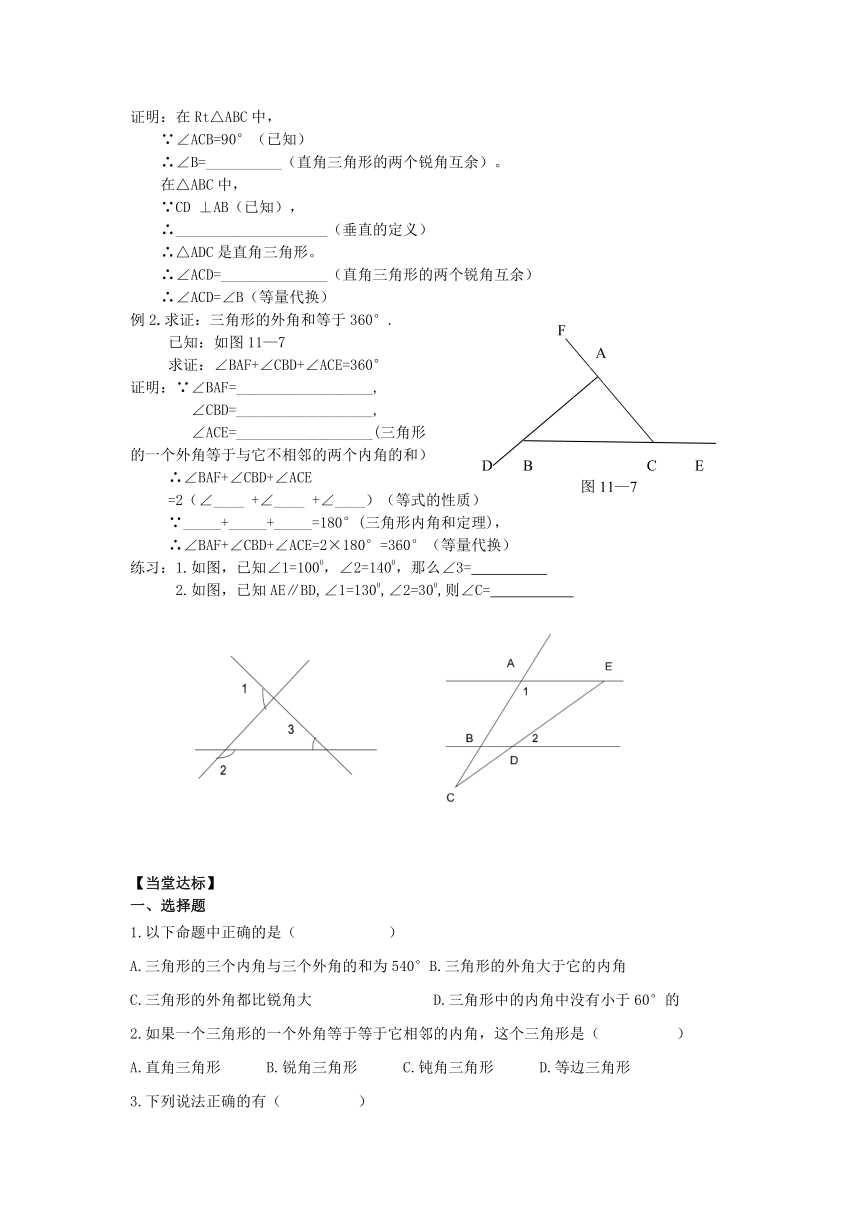
八年级数学(下)学案案(第十一章)
11.4三角形内角和定理(第2课时)
【学习目标】1.掌握三角形内角和定理和推论的应用;
2.经历探索三角形外角和的推理的过程,进一步培养推理能力;
3.通过探索三角形外角和的推理的活动,培养论证能力,拓宽解题思路。
【课前预习】
一、知识回顾:
1.三角形内角和定理的内容是什么?
2.三角形内角和定理的推论的内容是什么?
3.几何的证明步骤有哪些?
二、阅读课本127-128页的内容,解决下列问题。
1.小组探究:例1还有没有其它的解法?若有,能不能试着写出来。
2.三角形外角和定理: 。
三、练一练:
1.已知:如图,∠ACD是△ABC的外角,CE平分∠ACD,且BA∥CE。
求证:∠A=∠B
2.已知:如图,∠1=∠2,∠3=∠4,∠E=900.
求证:AB∥CD
【课中导学】
问题一:三角形的外角和定理是什么?
问题二:阅读课本127-128页例1、例2,解决下列问题。
例1.已知:如图11—6,在Rt△ABC中,∠ACB=90°,CD ⊥AB
求证:∠ACD=∠B
证明:在Rt△ABC中,
∵∠ACB=90°(已知)
∴∠B=__________(直角三角形的两个锐角互余)。
在△ABC中,
∵CD ⊥AB(已知),
∴____________________(垂直的定义)
∴△ADC是直角三角形。
∴∠ACD=______________(直角三角形的两个锐角互余)
∴∠ACD=∠B(等量代换)
例2.求证:三角形的外角和等于360°.
已知:如图11—7
求证:∠BAF+∠CBD+∠ACE=360°
证明:∵∠BAF=__________________,
∠CBD=__________________,
∠ACE=__________________(三角形
的一个外角等于与它不相邻的两个内角的和)
∴∠BAF+∠CBD+∠ACE
=2(∠____ +∠____ +∠____)(等式的性质)
∵_____+_____+_____=180°(三角形内角和定理),
∴∠BAF+∠CBD+∠ACE=2×180°=360°(等量代换)
练习:1.如图,已知∠1=1000,∠2=1400,那么∠3=
2.如图,已知AE∥BD,∠1=1300,∠2=300,则∠C=
【当堂达标】
一、选择题
1.以下命题中正确的是(??????) A.三角形的三个内角与三个外角的和为540°B.三角形的外角大于它的内角 C.三角形的外角都比锐角大 D.三角形中的内角中没有小于60°的
2.如果一个三角形的一个外角等于等于它相邻的内角,这个三角形是(?????) A.直角三角形???B.锐角三角形???C.钝角三角形???D.等边三角形
3.下列说法正确的有(?????)
①三角形的外角大于它的内角;②三角形的一个外角等于和它不相邻的两个内角之和;③三角形的外角中至少有两个钝角;④三角形的外角都是钝角.
A.1个?????B.2个?????C.3个??????D.4个
4.三角形的三个外角之比为2∶2∶3,则此三角形为(?????) A.锐角三角形? ?B.钝角三角形? ?C.直角三角形? ?D.等边三角形
5.如果一个三角形的一个内角大于相邻的外角,这个三角形是(?????) A.锐角三角形?? B.钝角三角形? ?C.直角三角形? ?D.等边三角形
二、解答题
6.如图D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数 (2)∠C的度数
7.如图,已知∠B=40°,∠C=59°,
∠DEC=47°,求∠F的度数。
【巩固训练】
1.在△ABC中, ∠A=40°,∠B=∠C,则∠C= 。
2.一个三角形三个内角度数的比是2∶3∶4,那么这个三角形是 三角形。
3.在△ABC中, ∠A-∠B=36°,∠C=2∠B,则∠A= ,∠B= ,∠C= 。
4.在△ABC中,已知∠A=2∠B=3∠C,请你判断三角形的形状。
5.如图,AD平分∠BAC,其中∠B=50°,∠ADC=80°,求∠BAC、∠C的度数。
6.已知:如图BD为∠ABC的平分线,CD为
△ABC的外角∠ACE的平分线,它与BD
交于D,求证:∠A=2∠D
11.4三角形内角和定理(第2课时)
【学习目标】1.掌握三角形内角和定理和推论的应用;
2.经历探索三角形外角和的推理的过程,进一步培养推理能力;
3.通过探索三角形外角和的推理的活动,培养论证能力,拓宽解题思路。
【课前预习】
一、知识回顾:
1.三角形内角和定理的内容是什么?
2.三角形内角和定理的推论的内容是什么?
3.几何的证明步骤有哪些?
二、阅读课本127-128页的内容,解决下列问题。
1.小组探究:例1还有没有其它的解法?若有,能不能试着写出来。
2.三角形外角和定理: 。
三、练一练:
1.已知:如图,∠ACD是△ABC的外角,CE平分∠ACD,且BA∥CE。
求证:∠A=∠B
2.已知:如图,∠1=∠2,∠3=∠4,∠E=900.
求证:AB∥CD
【课中导学】
问题一:三角形的外角和定理是什么?
问题二:阅读课本127-128页例1、例2,解决下列问题。
例1.已知:如图11—6,在Rt△ABC中,∠ACB=90°,CD ⊥AB
求证:∠ACD=∠B
证明:在Rt△ABC中,
∵∠ACB=90°(已知)
∴∠B=__________(直角三角形的两个锐角互余)。
在△ABC中,
∵CD ⊥AB(已知),
∴____________________(垂直的定义)
∴△ADC是直角三角形。
∴∠ACD=______________(直角三角形的两个锐角互余)
∴∠ACD=∠B(等量代换)
例2.求证:三角形的外角和等于360°.
已知:如图11—7
求证:∠BAF+∠CBD+∠ACE=360°
证明:∵∠BAF=__________________,
∠CBD=__________________,
∠ACE=__________________(三角形
的一个外角等于与它不相邻的两个内角的和)
∴∠BAF+∠CBD+∠ACE
=2(∠____ +∠____ +∠____)(等式的性质)
∵_____+_____+_____=180°(三角形内角和定理),
∴∠BAF+∠CBD+∠ACE=2×180°=360°(等量代换)
练习:1.如图,已知∠1=1000,∠2=1400,那么∠3=
2.如图,已知AE∥BD,∠1=1300,∠2=300,则∠C=
【当堂达标】
一、选择题
1.以下命题中正确的是(??????) A.三角形的三个内角与三个外角的和为540°B.三角形的外角大于它的内角 C.三角形的外角都比锐角大 D.三角形中的内角中没有小于60°的
2.如果一个三角形的一个外角等于等于它相邻的内角,这个三角形是(?????) A.直角三角形???B.锐角三角形???C.钝角三角形???D.等边三角形
3.下列说法正确的有(?????)
①三角形的外角大于它的内角;②三角形的一个外角等于和它不相邻的两个内角之和;③三角形的外角中至少有两个钝角;④三角形的外角都是钝角.
A.1个?????B.2个?????C.3个??????D.4个
4.三角形的三个外角之比为2∶2∶3,则此三角形为(?????) A.锐角三角形? ?B.钝角三角形? ?C.直角三角形? ?D.等边三角形
5.如果一个三角形的一个内角大于相邻的外角,这个三角形是(?????) A.锐角三角形?? B.钝角三角形? ?C.直角三角形? ?D.等边三角形
二、解答题
6.如图D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.
求:(1)∠B的度数 (2)∠C的度数
7.如图,已知∠B=40°,∠C=59°,
∠DEC=47°,求∠F的度数。
【巩固训练】
1.在△ABC中, ∠A=40°,∠B=∠C,则∠C= 。
2.一个三角形三个内角度数的比是2∶3∶4,那么这个三角形是 三角形。
3.在△ABC中, ∠A-∠B=36°,∠C=2∠B,则∠A= ,∠B= ,∠C= 。
4.在△ABC中,已知∠A=2∠B=3∠C,请你判断三角形的形状。
5.如图,AD平分∠BAC,其中∠B=50°,∠ADC=80°,求∠BAC、∠C的度数。
6.已知:如图BD为∠ABC的平分线,CD为
△ABC的外角∠ACE的平分线,它与BD
交于D,求证:∠A=2∠D
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
