3.1匀速圆周运动快慢的描述 同步练习(Word版含解析)
文档属性
| 名称 | 3.1匀速圆周运动快慢的描述 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-04-14 07:55:08 | ||
图片预览


文档简介
鲁科版 (2019)必修第二册 3.1 匀速圆周运动快慢的描述 同步练习
一、单选题
1.如图所示,拖拉机后轮的半径大于前轮半径,A和B是前轮和后轮边缘上的点,若车行进时车轮没有打滑,则A、B两点( )
A.周期相等 B.角速度相同
C.线速度大小相等 D.向心加速度大小相等
2.如图“旋转纽扣”游戏。现用力反复拉线两端,纽扣逆顺转动交替,纽扣绕其中心转速最大可达10 r/s。则可知纽扣边缘各质点绕其中心( )
A.线速度在同一时刻相同,且可能在变小
B.线速度在同一时刻相同,且一直在变大
C.角速度在同一时刻相同,且可能在变小
D.角速度在同一时刻相同,且一直在变大
3.如图所示,是杭州G20演出过程中的一个场景——由全息技术产生的一把巨大的扇子正徐徐打开,则下列关于扇面上A、B两点(这两点跟着扇面打开转动,始终处于同一个圆的同一条半径上)说法正确的是( )
A.A、B两点在相同时内的位移相同 B.A、B两点在相同时间内的路程相同
C.A点的角速度比B点大 D.A点的线速度比B点大
4.家用台式计算机上的硬磁盘的磁道和区如图所示,某台计算机上的硬磁盘共有9216个磁道(即9216个不同半径的同心圆),每个磁道分8192个扇区(每扇区为圆周),每个扇区可以记录512个字节,电动机使磁盘以7200r/min的转速匀速转动,磁头在读、写数据时是不动的,磁盘每转一圈,磁头沿半径方向跳动一个磁道,下列选项正确的是( )
A.每个字节在磁道上所占用的磁道长度都相同
B.磁盘转动的角速度是240rad/s
C.一个扇区通过磁头所用的时间为1.7×10-3s
D.不计磁头转移磁道的时间,1s内最多可以从一个硬盘面上读取5.0×108个字节
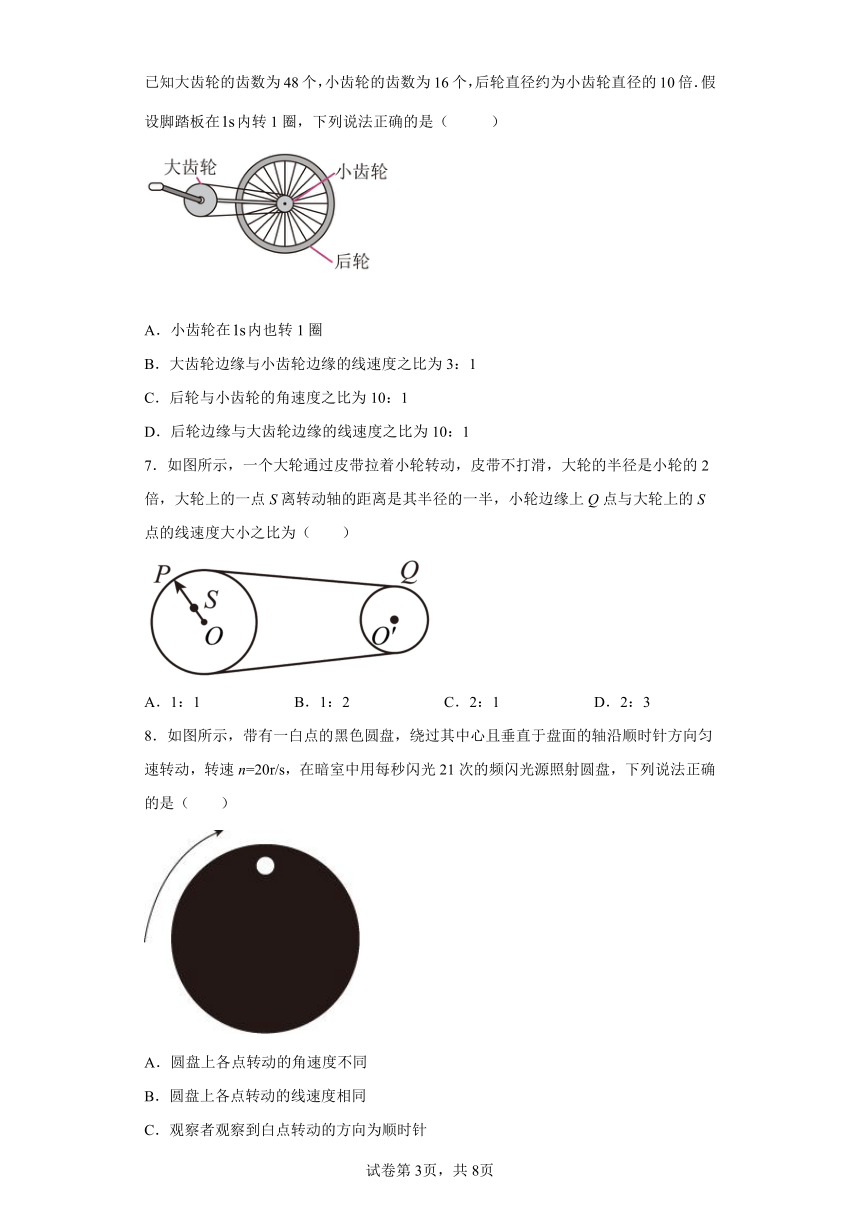
5.无级变速是在变速范围内任意连续变换速度的变速系统。如图所示是无级变速模型示意图,主动轮、从动轮中间有一个滚轮,各轮间不打滑,通过滚轮位置改变实现无级变速。A、B为滚轮轴上两点,则( )
A.从动轮和主动轮转动方向始终相反
B.滚轮在A处,从动轮转速大于主动轮转速
C.滚轮在B处,从动轮转速大于主动轮转速
D.滚轮从A到B,从动轮转速先变大后变小
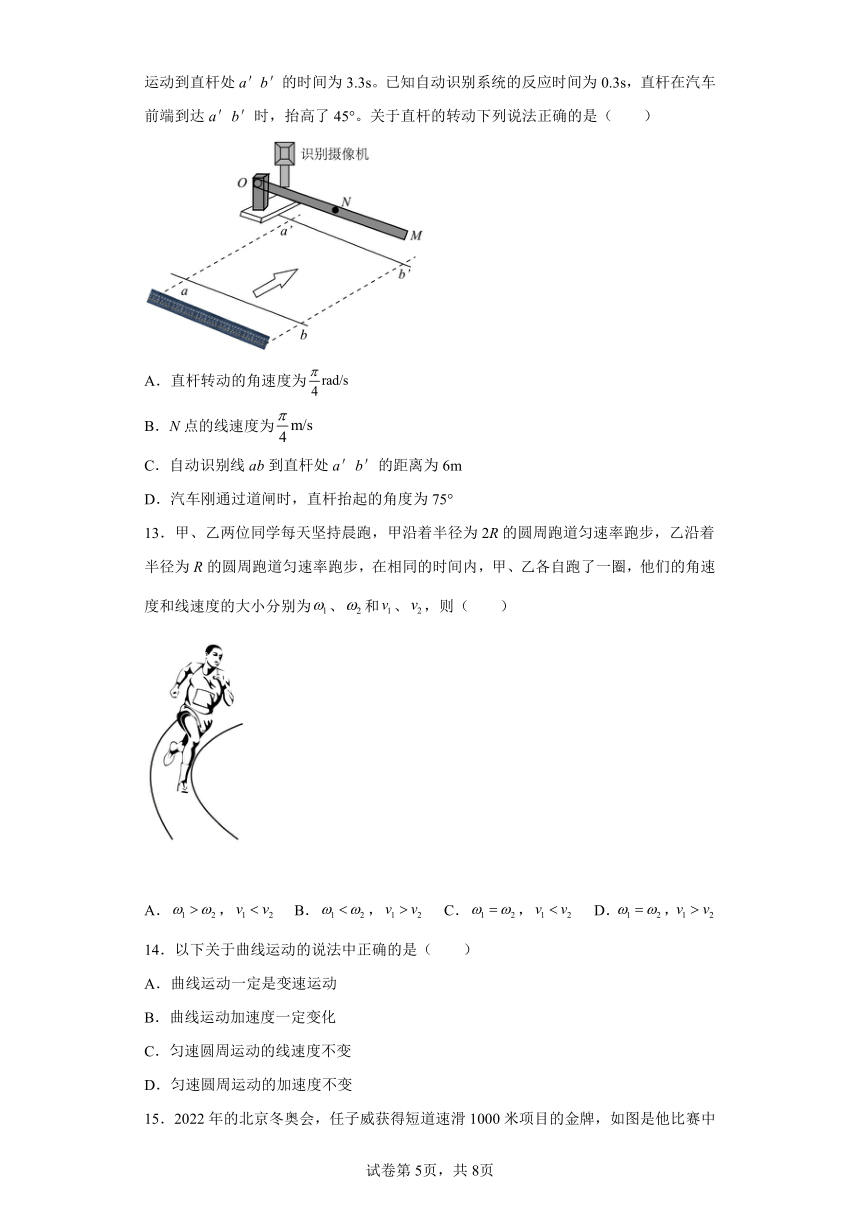
6.如图所示是利用两个大小不同的齿轮来达到改变转速的自行车传动结构的示意图。已知大齿轮的齿数为48个,小齿轮的齿数为16个,后轮直径约为小齿轮直径的10倍.假设脚踏板在内转1圈,下列说法正确的是( )
A.小齿轮在内也转1圈
B.大齿轮边缘与小齿轮边缘的线速度之比为3:1
C.后轮与小齿轮的角速度之比为10:1
D.后轮边缘与大齿轮边缘的线速度之比为10:1
7.如图所示,一个大轮通过皮带拉着小轮转动,皮带不打滑,大轮的半径是小轮的2倍,大轮上的一点S离转动轴的距离是其半径的一半,小轮边缘上Q点与大轮上的S点的线速度大小之比为( )
A.1:1 B.1:2 C.2:1 D.2:3
8.如图所示,带有一白点的黑色圆盘,绕过其中心且垂直于盘面的轴沿顺时针方向匀速转动,转速n=20r/s,在暗室中用每秒闪光21次的频闪光源照射圆盘,下列说法正确的是( )
A.圆盘上各点转动的角速度不同
B.圆盘上各点转动的线速度相同
C.观察者观察到白点转动的方向为顺时针
D.观察者观察到白点转动的周期T=1s
9.如图所示,压路机后轮的半径是前轮半径的两倍,为前轮边缘上的一点,为后轮上一点,它离后轮轴的距离是后轮半径的一半,轮子不打滑,则的角速度之比为( )
A. B. C. D.
10.如图所示为“行星传动示意图”。中心“太阳轮”的转动轴固定,其半径为,周围四个“行星轮”的转动轴固定,其半径为,“齿圈”的半径为,其中分别是“太阳轮”“行星轮”“齿圈”边缘上的点,那么( )
A.点与点的角速度相同 B.点与点的角速度相同
C.点与点的转速之比为 D.点与点的周期之比为
11.小红同学在体验糕点制作“裱花”环节时,她在绕中心匀速转动的圆盘上放了一块直径8英寸(20 cm)的蛋糕,在蛋糕边缘每隔4 s均匀“点”一次奶油,蛋糕转动一周正好均匀“点”上15点奶油。下列说法中正确的是( )
A.圆盘转动的转速约为2π r/min
B.圆盘转动的角速度大小为rad/s
C.蛋糕边缘的线速度大小约为m/s
D.蛋糕边缘的半个周期内的平均速度约为0 m/s
12.随着车辆的增多,很多地方都安装有车牌自动识别的直杆道闸。如图所示为某直杆道闸OM,OM长度为3m,N点为OM中点,直杆可绕转轴O在竖直平面内匀速转动。一辆长度为4m的汽车以速度v=2m/s垂直于自动识别线ab匀速运动,汽车前端从ab运动到直杆处a'b'的时间为3.3s。已知自动识别系统的反应时间为0.3s,直杆在汽车前端到达a'b'时,抬高了45°。关于直杆的转动下列说法正确的是( )
A.直杆转动的角速度为
B.N点的线速度为
C.自动识别线ab到直杆处a'b'的距离为6m
D.汽车刚通过道闸时,直杆抬起的角度为75°
13.甲、乙两位同学每天坚持晨跑,甲沿着半径为2R的圆周跑道匀速率跑步,乙沿着半径为R的圆周跑道匀速率跑步,在相同的时间内,甲、乙各自跑了一圈,他们的角速度和线速度的大小分别为、和、,则( )
A., B., C., D.,
14.以下关于曲线运动的说法中正确的是( )
A.曲线运动一定是变速运动
B.曲线运动加速度一定变化
C.匀速圆周运动的线速度不变
D.匀速圆周运动的加速度不变
15.2022年的北京冬奥会,任子威获得短道速滑1000米项目的金牌,如图是他比赛中正沿圆弧形弯道匀速率滑行,则他( )
A.所受的合力为零,做匀速运动
B.所受的合力恒定,做匀加速运动
C.所受的合力变化,做变加速运动
D.所受的合力恒定,做变加速运动
二、填空题
16.如图所示,一个物体环绕中心线OO′以角速度匀速转动,=,A、B两点的角速度之比为_____,A、B两点的线速度之比为_____。
17.如图所示,皮带在传动的过程中无打滑现象,大轮的半径R为40cm,小轮的半径r为20cm,又O1C=10cm,则A、B两点的线速度大小之比vA:vB=____,B、C两点的角速度大小之比ωB:ωC=__________。
18.写出线速度和角速度的几个常用表达式。
(1)v=____________=____________;
(2)=____________=____________。
三、解答题
19.抛石机是古代远程攻击的一种重型武器,某同学制作了一个简易模型,如图所示。支架固定在地面上,O为转轴,长为L的轻质硬杆A端的凹槽内放置一石块,B端固定重物,AO=0.9L,BO=0.1L。为增大射程,在重物B上施加一向下的瞬时作用力后,硬杆绕O点在竖直平面内转动。硬杆转动到竖直位置时,石块立即被水平抛出,此时重物的速度为,石块直接击中前方倾角为15°的斜坡,且击中斜坡时的速度方向与斜坡成60°角,重力加速度为g,忽略空气阻力影响。求:
(1)石块击中斜坡时的速度大小;
(2)石块抛出后在空中运动的水平距离。
20.一人骑自行车由静止开始上一长 L=202m ,斜坡坡度为0.05(沿斜坡前进100m,高度上升5m),自行车达到最大速度前做加速度 a=2m/s2 的匀加速直线运动,达到最大速度后脚蹬踏板使大齿轮以转/秒的转速匀角速转动,自行车匀速运动一段时间后,由于骑行者体能下降,自行车距离坡顶 50m 处开始做匀减速运动,已知最后 50m 的平均速度只有之前平均速度的 84%,自行车大齿轮直径 d1=20cm,小齿轮直径d2=6cm,车轮直径 d3=60cm。求:
(1)大齿轮 的最大角速度1;
(2)运动过程中自行车的最大速度vm。
(3)到达坡顶时的速度v。
21.如图所示,小球P用长L =1m的细绳系着,在水平面内绕O点做匀速圆周运动,其角速度ω= 2π(rad/s)。另一质量m = 1kg的小球Q放在高出水平面h = 0.8m的光滑水平槽上,槽与绳平行,槽口A点在O点正上方当小球Q受到水平恒力F作用开始运动时,小球P恰好运动到如图所示位置,Q运动到A时,力F自然取消。(g取10 m/s2),不计空气阻力。求∶
(1)若两小球相碰,恒力F的表达式∶ (用m、L、ω、h、g表示)
(2)在满足(1)条件的前提下,求Q运动到槽口的最短时间和相应的Q在槽上滑行的距离。
22.如图所示为一自行车的局部结构示意图,设连接脚踏板的连杆长为L1,由脚踏板带动半径为r1的大轮盘(牙盘),通过链条与半径为r2的小轮盘(飞轮)连接,小轮盘带动半径为R的后轮转动,使自行车在水平路面上匀速前进。
(1)自行车牙盘的半径一般要大于飞轮的半径,想想看,这是为什么?
(2)设L1=18cm,r1=12cm,r2=6cm,R=30cm,为了维持自行车以v=3m/s的速度在水平路面上匀速行驶,请你计算一下每分钟要踩脚踏板几圈。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【详解】
车行进时不打滑,说明车轮边缘各点的线速度大小相等,由于两轮的半径不同所以A、B两点的角速度、周期、向心加速度大小都不相同。
故选C。
2.C
【详解】
AB.纽扣边缘各质点是同圆心转动,同一时刻角速度相同,转动的半径相同,由线速度公式可知,纽扣边缘各质点的线速度在同一时刻大小相同,由于线速度是有大小,又有方向的物理量,边缘不同位置的质点的线速度方向不同,所以纽扣边缘各质点绕其中心转动的线速度在同一时刻不相同;且可能在变小,不会一直在变大,AB错误;
CD.由于纽扣边缘各质点是同圆心转动,所以角速度在同一时刻相同,且可能在变小,可能不会一直在变大,C正确,D错误。
故选C。
3.D
【详解】
由于A、B两点在同一个扇面上转动,所以两点的角速度相等,根据v=ωr可知A点的线速度比B点大,所以在相同时间内A点的路程比B点大。根据几何关系可知,相同时间内A点的位移比B点大,故ABC错误,D正确。
故选D。
4.D
【详解】
A.每个磁道扇区数相同,每个扇区可记录字节数相同,即每个磁道上可记录字节数相同,但半径不同,所以不同磁道上每个字节所占用的长度不同,故A错误;
B.电动机使磁盘以7200r/min的转速匀速转动,磁盘转动的角速度是
故B错误;
C.经过一个扇区转过的圆心角为:,故经过一个扇区用时为:
故C错误;
D.转速为n=7200r/min=120r/s,则计算机在1s内从磁盘面上读取的字节数
N=120×8192×512=5.0×108(字节)
故D正确。
故选D。
5.B
【详解】
A.主动轮和滚轮之间为摩擦传动,转动方向相反,滚轮和从动轮之间为摩擦传动,转动方向相反,则主动轮和从动轮转动方向相同,故A错误;
BC.摩擦传动,线速度相等,则从动轮和主动轮的线速度相等,设主动轮和从动轮线速度分别为、即
又因为
故
由图可得滚轮在A处时
故
又
则有
同理在B处,因,则有,故,故B正确,C错误;
D.由图可得滚轮从A到B,主动轮转动的角速度不变,线速度逐渐变小,从动轮的线速度等于主动轮的线速度,则从动轮转速一直变小,故D错误。
故选B。
6.D
【详解】
AB.齿轮的齿数与半径成正比,因此大齿轮的半径是小齿轮半径的3倍,大齿轮与小齿轮是链条传动,边缘点线速度大小相等,令大齿轮为A,小齿轮为B,后轮边缘为C,故
vA:vB=1:1
又
rA:rB=3:1
根据
v=ωr
可知,大齿轮与小齿轮的角速度之比
ωA:ωB=rB:rA=1:3
所以脚踏板在内转1圈,小齿轮在内转3圈,故AB错误;
CD.B、C两点为同轴转动,所以
ωB:ωC=1:1
根据
v=ωr
可知,后轮边缘上C点的线速度与小齿轮边缘上B点的线速度之比
vC:vB=rC:rB=10:1
故C错误,D正确。
故选D。
7.C
【详解】
P与Q用不打滑的皮带连接,线速度大小相等,有
又P与S同轴转动,角速度相等,由
由于
则
联立可得
故选C。
8.D
【详解】
AB.圆盘上各点转动的角速度相同,线速度不同,AB错误;
CD.因为沿顺时针方向旋转20圈,即
在暗室中用每秒闪光21次的频闪光源照射圆盘,即
可得
所以观察到白点逆时针旋转
所以,观察到白点每秒逆时针旋转1圈,即有周期
C错误,D正确。
故选D。
9.B
【详解】
前后轮边缘的线速度大小相等,根据可知,的角速度之比,即前后轮的角速度之比为
故选B。
10.C
【详解】
由题意可知,三点的线速度大小相等,根据可知
根据可得转速之比为
根据得
故选C。
11.B
【详解】
A.由题意可知,蛋糕转动的周期为
则圆盘转动的转速约为,A错误;
B.圆盘转动的角速度大小为
B正确;
C.蛋糕边缘的线速度大小约为
C错误;
D.蛋糕半个周期内的平均速度约为
故D错误;
故选B。
12.D
【详解】
A.由角速度定义式
A错误;
B.由角速度与线速度关系式
B错误;
C.有匀速直线运动公式
C错误;
D.由匀速直线运动公式,车通过道闸的时间为
由角速度定义式
求得
D正确。
故选D。
13.D
【详解】
甲、乙在相同的时间内都跑了一圈,根据
则
甲晨跑的半径为2R,乙晨跑的半径为R,根据
则
故选D。
14.A
【详解】
A.曲线运动的速度沿轨迹的切线方向,时刻变化,一定是变速运动,选项A正确;
B.曲线运动的合力有可能是恒定的,如平抛运动,为匀变速曲线运动,选项B错误;
C.匀速圆周运动的线速度大小不变,方向时刻改变,选项C错误;
D.匀速圆周运动的加速度指向圆心,方向时刻变化,选项D错误。
故选A。
15.C
【详解】
根据题意可知,运动员做匀速圆周运动。合力大小不变,但方向改变,合力变化,做变加速运动。故选项C正确。
16. 1:1
【详解】
[1]共轴转动的各点角速度相等,则A、B两点的角速度相等即A、B两点的角速度之比为1:1
[2]A点的转动半径为
B点的转动半径为
根据v=rω公式,线速度之比
17. 1:1 2:1
【详解】
[1]A、B两轮为皮带传动,边缘点线速度大小相等,故
[2]又由于
根据
得
A、C为为同轴转动,角速度相等,故
故
18.
【详解】
(1)[1][2]线速度的表达式为
(2)[3][4]角速度的表达式为
19.(1);(2)
【详解】
(1)设重物转至最低点时的速度为v1,石块转至最高点时的速度为v2,则
。
根据同轴转动角速度相等,由
得
解得
设石块击中斜坡时的速度为v3,将v3分解如图所示
据几何知识得
解得
(2)据几何知识得
竖直方向上
水平方向
联立解得
20.(1)8rad/s;(2)8m/s;(3)4.16m/s
【详解】
(1)大齿轮 的最大角速度
ω1=2πn=8rad/s
(2)运动过程中自行车的最大速度
(3)到达最大速度时的位移
匀加速的时间
匀速的时间
加速和匀速阶段的平均速度
减速阶段
解得
v=4.16m/s
21.(1) ;(2),
【详解】
(1)为了保证两球相碰,球Q从A点飞出水平射程为L,设飞出时的速度为v,则有
,
A在水平面上有
,
要使两球相碰应有
联立解得
(2)由(1)可知,k=0,Q运动到槽口的时间最短,则有
最小拉力为
Q在槽上滑行的距离为x,则有
代入数据解得
22.(1)见解析;(2)48圈
【详解】
(1)通过链条相连的牙盘和飞轮边缘的线速度相同,当牙盘的半径大于飞轮的半径时,由v=ωr知,牙盘的角速度小于飞轮的角速度,即人踩脚踏板的角速度小于后轮的角速度,这样即使脚蹬得慢,自行车也能获得较快的速度;
(2)自行车行进的速度等于后轮边缘上某点绕转轴转动的线速度。设牙盘转动的角速度为ω1,自行车后轮转动的角速度,即飞轮的角速度为ω2,人踩脚踏板的转速为n,则
由于
解得
即每分钟要踩脚踏板48圈。
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图所示,拖拉机后轮的半径大于前轮半径,A和B是前轮和后轮边缘上的点,若车行进时车轮没有打滑,则A、B两点( )
A.周期相等 B.角速度相同
C.线速度大小相等 D.向心加速度大小相等
2.如图“旋转纽扣”游戏。现用力反复拉线两端,纽扣逆顺转动交替,纽扣绕其中心转速最大可达10 r/s。则可知纽扣边缘各质点绕其中心( )
A.线速度在同一时刻相同,且可能在变小
B.线速度在同一时刻相同,且一直在变大
C.角速度在同一时刻相同,且可能在变小
D.角速度在同一时刻相同,且一直在变大
3.如图所示,是杭州G20演出过程中的一个场景——由全息技术产生的一把巨大的扇子正徐徐打开,则下列关于扇面上A、B两点(这两点跟着扇面打开转动,始终处于同一个圆的同一条半径上)说法正确的是( )
A.A、B两点在相同时内的位移相同 B.A、B两点在相同时间内的路程相同
C.A点的角速度比B点大 D.A点的线速度比B点大
4.家用台式计算机上的硬磁盘的磁道和区如图所示,某台计算机上的硬磁盘共有9216个磁道(即9216个不同半径的同心圆),每个磁道分8192个扇区(每扇区为圆周),每个扇区可以记录512个字节,电动机使磁盘以7200r/min的转速匀速转动,磁头在读、写数据时是不动的,磁盘每转一圈,磁头沿半径方向跳动一个磁道,下列选项正确的是( )
A.每个字节在磁道上所占用的磁道长度都相同
B.磁盘转动的角速度是240rad/s
C.一个扇区通过磁头所用的时间为1.7×10-3s
D.不计磁头转移磁道的时间,1s内最多可以从一个硬盘面上读取5.0×108个字节
5.无级变速是在变速范围内任意连续变换速度的变速系统。如图所示是无级变速模型示意图,主动轮、从动轮中间有一个滚轮,各轮间不打滑,通过滚轮位置改变实现无级变速。A、B为滚轮轴上两点,则( )
A.从动轮和主动轮转动方向始终相反
B.滚轮在A处,从动轮转速大于主动轮转速
C.滚轮在B处,从动轮转速大于主动轮转速
D.滚轮从A到B,从动轮转速先变大后变小
6.如图所示是利用两个大小不同的齿轮来达到改变转速的自行车传动结构的示意图。已知大齿轮的齿数为48个,小齿轮的齿数为16个,后轮直径约为小齿轮直径的10倍.假设脚踏板在内转1圈,下列说法正确的是( )
A.小齿轮在内也转1圈
B.大齿轮边缘与小齿轮边缘的线速度之比为3:1
C.后轮与小齿轮的角速度之比为10:1
D.后轮边缘与大齿轮边缘的线速度之比为10:1
7.如图所示,一个大轮通过皮带拉着小轮转动,皮带不打滑,大轮的半径是小轮的2倍,大轮上的一点S离转动轴的距离是其半径的一半,小轮边缘上Q点与大轮上的S点的线速度大小之比为( )
A.1:1 B.1:2 C.2:1 D.2:3
8.如图所示,带有一白点的黑色圆盘,绕过其中心且垂直于盘面的轴沿顺时针方向匀速转动,转速n=20r/s,在暗室中用每秒闪光21次的频闪光源照射圆盘,下列说法正确的是( )
A.圆盘上各点转动的角速度不同
B.圆盘上各点转动的线速度相同
C.观察者观察到白点转动的方向为顺时针
D.观察者观察到白点转动的周期T=1s
9.如图所示,压路机后轮的半径是前轮半径的两倍,为前轮边缘上的一点,为后轮上一点,它离后轮轴的距离是后轮半径的一半,轮子不打滑,则的角速度之比为( )
A. B. C. D.
10.如图所示为“行星传动示意图”。中心“太阳轮”的转动轴固定,其半径为,周围四个“行星轮”的转动轴固定,其半径为,“齿圈”的半径为,其中分别是“太阳轮”“行星轮”“齿圈”边缘上的点,那么( )
A.点与点的角速度相同 B.点与点的角速度相同
C.点与点的转速之比为 D.点与点的周期之比为
11.小红同学在体验糕点制作“裱花”环节时,她在绕中心匀速转动的圆盘上放了一块直径8英寸(20 cm)的蛋糕,在蛋糕边缘每隔4 s均匀“点”一次奶油,蛋糕转动一周正好均匀“点”上15点奶油。下列说法中正确的是( )
A.圆盘转动的转速约为2π r/min
B.圆盘转动的角速度大小为rad/s
C.蛋糕边缘的线速度大小约为m/s
D.蛋糕边缘的半个周期内的平均速度约为0 m/s
12.随着车辆的增多,很多地方都安装有车牌自动识别的直杆道闸。如图所示为某直杆道闸OM,OM长度为3m,N点为OM中点,直杆可绕转轴O在竖直平面内匀速转动。一辆长度为4m的汽车以速度v=2m/s垂直于自动识别线ab匀速运动,汽车前端从ab运动到直杆处a'b'的时间为3.3s。已知自动识别系统的反应时间为0.3s,直杆在汽车前端到达a'b'时,抬高了45°。关于直杆的转动下列说法正确的是( )
A.直杆转动的角速度为
B.N点的线速度为
C.自动识别线ab到直杆处a'b'的距离为6m
D.汽车刚通过道闸时,直杆抬起的角度为75°
13.甲、乙两位同学每天坚持晨跑,甲沿着半径为2R的圆周跑道匀速率跑步,乙沿着半径为R的圆周跑道匀速率跑步,在相同的时间内,甲、乙各自跑了一圈,他们的角速度和线速度的大小分别为、和、,则( )
A., B., C., D.,
14.以下关于曲线运动的说法中正确的是( )
A.曲线运动一定是变速运动
B.曲线运动加速度一定变化
C.匀速圆周运动的线速度不变
D.匀速圆周运动的加速度不变
15.2022年的北京冬奥会,任子威获得短道速滑1000米项目的金牌,如图是他比赛中正沿圆弧形弯道匀速率滑行,则他( )
A.所受的合力为零,做匀速运动
B.所受的合力恒定,做匀加速运动
C.所受的合力变化,做变加速运动
D.所受的合力恒定,做变加速运动
二、填空题
16.如图所示,一个物体环绕中心线OO′以角速度匀速转动,=,A、B两点的角速度之比为_____,A、B两点的线速度之比为_____。
17.如图所示,皮带在传动的过程中无打滑现象,大轮的半径R为40cm,小轮的半径r为20cm,又O1C=10cm,则A、B两点的线速度大小之比vA:vB=____,B、C两点的角速度大小之比ωB:ωC=__________。
18.写出线速度和角速度的几个常用表达式。
(1)v=____________=____________;
(2)=____________=____________。
三、解答题
19.抛石机是古代远程攻击的一种重型武器,某同学制作了一个简易模型,如图所示。支架固定在地面上,O为转轴,长为L的轻质硬杆A端的凹槽内放置一石块,B端固定重物,AO=0.9L,BO=0.1L。为增大射程,在重物B上施加一向下的瞬时作用力后,硬杆绕O点在竖直平面内转动。硬杆转动到竖直位置时,石块立即被水平抛出,此时重物的速度为,石块直接击中前方倾角为15°的斜坡,且击中斜坡时的速度方向与斜坡成60°角,重力加速度为g,忽略空气阻力影响。求:
(1)石块击中斜坡时的速度大小;
(2)石块抛出后在空中运动的水平距离。
20.一人骑自行车由静止开始上一长 L=202m ,斜坡坡度为0.05(沿斜坡前进100m,高度上升5m),自行车达到最大速度前做加速度 a=2m/s2 的匀加速直线运动,达到最大速度后脚蹬踏板使大齿轮以转/秒的转速匀角速转动,自行车匀速运动一段时间后,由于骑行者体能下降,自行车距离坡顶 50m 处开始做匀减速运动,已知最后 50m 的平均速度只有之前平均速度的 84%,自行车大齿轮直径 d1=20cm,小齿轮直径d2=6cm,车轮直径 d3=60cm。求:
(1)大齿轮 的最大角速度1;
(2)运动过程中自行车的最大速度vm。
(3)到达坡顶时的速度v。
21.如图所示,小球P用长L =1m的细绳系着,在水平面内绕O点做匀速圆周运动,其角速度ω= 2π(rad/s)。另一质量m = 1kg的小球Q放在高出水平面h = 0.8m的光滑水平槽上,槽与绳平行,槽口A点在O点正上方当小球Q受到水平恒力F作用开始运动时,小球P恰好运动到如图所示位置,Q运动到A时,力F自然取消。(g取10 m/s2),不计空气阻力。求∶
(1)若两小球相碰,恒力F的表达式∶ (用m、L、ω、h、g表示)
(2)在满足(1)条件的前提下,求Q运动到槽口的最短时间和相应的Q在槽上滑行的距离。
22.如图所示为一自行车的局部结构示意图,设连接脚踏板的连杆长为L1,由脚踏板带动半径为r1的大轮盘(牙盘),通过链条与半径为r2的小轮盘(飞轮)连接,小轮盘带动半径为R的后轮转动,使自行车在水平路面上匀速前进。
(1)自行车牙盘的半径一般要大于飞轮的半径,想想看,这是为什么?
(2)设L1=18cm,r1=12cm,r2=6cm,R=30cm,为了维持自行车以v=3m/s的速度在水平路面上匀速行驶,请你计算一下每分钟要踩脚踏板几圈。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【详解】
车行进时不打滑,说明车轮边缘各点的线速度大小相等,由于两轮的半径不同所以A、B两点的角速度、周期、向心加速度大小都不相同。
故选C。
2.C
【详解】
AB.纽扣边缘各质点是同圆心转动,同一时刻角速度相同,转动的半径相同,由线速度公式可知,纽扣边缘各质点的线速度在同一时刻大小相同,由于线速度是有大小,又有方向的物理量,边缘不同位置的质点的线速度方向不同,所以纽扣边缘各质点绕其中心转动的线速度在同一时刻不相同;且可能在变小,不会一直在变大,AB错误;
CD.由于纽扣边缘各质点是同圆心转动,所以角速度在同一时刻相同,且可能在变小,可能不会一直在变大,C正确,D错误。
故选C。
3.D
【详解】
由于A、B两点在同一个扇面上转动,所以两点的角速度相等,根据v=ωr可知A点的线速度比B点大,所以在相同时间内A点的路程比B点大。根据几何关系可知,相同时间内A点的位移比B点大,故ABC错误,D正确。
故选D。
4.D
【详解】
A.每个磁道扇区数相同,每个扇区可记录字节数相同,即每个磁道上可记录字节数相同,但半径不同,所以不同磁道上每个字节所占用的长度不同,故A错误;
B.电动机使磁盘以7200r/min的转速匀速转动,磁盘转动的角速度是
故B错误;
C.经过一个扇区转过的圆心角为:,故经过一个扇区用时为:
故C错误;
D.转速为n=7200r/min=120r/s,则计算机在1s内从磁盘面上读取的字节数
N=120×8192×512=5.0×108(字节)
故D正确。
故选D。
5.B
【详解】
A.主动轮和滚轮之间为摩擦传动,转动方向相反,滚轮和从动轮之间为摩擦传动,转动方向相反,则主动轮和从动轮转动方向相同,故A错误;
BC.摩擦传动,线速度相等,则从动轮和主动轮的线速度相等,设主动轮和从动轮线速度分别为、即
又因为
故
由图可得滚轮在A处时
故
又
则有
同理在B处,因,则有,故,故B正确,C错误;
D.由图可得滚轮从A到B,主动轮转动的角速度不变,线速度逐渐变小,从动轮的线速度等于主动轮的线速度,则从动轮转速一直变小,故D错误。
故选B。
6.D
【详解】
AB.齿轮的齿数与半径成正比,因此大齿轮的半径是小齿轮半径的3倍,大齿轮与小齿轮是链条传动,边缘点线速度大小相等,令大齿轮为A,小齿轮为B,后轮边缘为C,故
vA:vB=1:1
又
rA:rB=3:1
根据
v=ωr
可知,大齿轮与小齿轮的角速度之比
ωA:ωB=rB:rA=1:3
所以脚踏板在内转1圈,小齿轮在内转3圈,故AB错误;
CD.B、C两点为同轴转动,所以
ωB:ωC=1:1
根据
v=ωr
可知,后轮边缘上C点的线速度与小齿轮边缘上B点的线速度之比
vC:vB=rC:rB=10:1
故C错误,D正确。
故选D。
7.C
【详解】
P与Q用不打滑的皮带连接,线速度大小相等,有
又P与S同轴转动,角速度相等,由
由于
则
联立可得
故选C。
8.D
【详解】
AB.圆盘上各点转动的角速度相同,线速度不同,AB错误;
CD.因为沿顺时针方向旋转20圈,即
在暗室中用每秒闪光21次的频闪光源照射圆盘,即
可得
所以观察到白点逆时针旋转
所以,观察到白点每秒逆时针旋转1圈,即有周期
C错误,D正确。
故选D。
9.B
【详解】
前后轮边缘的线速度大小相等,根据可知,的角速度之比,即前后轮的角速度之比为
故选B。
10.C
【详解】
由题意可知,三点的线速度大小相等,根据可知
根据可得转速之比为
根据得
故选C。
11.B
【详解】
A.由题意可知,蛋糕转动的周期为
则圆盘转动的转速约为,A错误;
B.圆盘转动的角速度大小为
B正确;
C.蛋糕边缘的线速度大小约为
C错误;
D.蛋糕半个周期内的平均速度约为
故D错误;
故选B。
12.D
【详解】
A.由角速度定义式
A错误;
B.由角速度与线速度关系式
B错误;
C.有匀速直线运动公式
C错误;
D.由匀速直线运动公式,车通过道闸的时间为
由角速度定义式
求得
D正确。
故选D。
13.D
【详解】
甲、乙在相同的时间内都跑了一圈,根据
则
甲晨跑的半径为2R,乙晨跑的半径为R,根据
则
故选D。
14.A
【详解】
A.曲线运动的速度沿轨迹的切线方向,时刻变化,一定是变速运动,选项A正确;
B.曲线运动的合力有可能是恒定的,如平抛运动,为匀变速曲线运动,选项B错误;
C.匀速圆周运动的线速度大小不变,方向时刻改变,选项C错误;
D.匀速圆周运动的加速度指向圆心,方向时刻变化,选项D错误。
故选A。
15.C
【详解】
根据题意可知,运动员做匀速圆周运动。合力大小不变,但方向改变,合力变化,做变加速运动。故选项C正确。
16. 1:1
【详解】
[1]共轴转动的各点角速度相等,则A、B两点的角速度相等即A、B两点的角速度之比为1:1
[2]A点的转动半径为
B点的转动半径为
根据v=rω公式,线速度之比
17. 1:1 2:1
【详解】
[1]A、B两轮为皮带传动,边缘点线速度大小相等,故
[2]又由于
根据
得
A、C为为同轴转动,角速度相等,故
故
18.
【详解】
(1)[1][2]线速度的表达式为
(2)[3][4]角速度的表达式为
19.(1);(2)
【详解】
(1)设重物转至最低点时的速度为v1,石块转至最高点时的速度为v2,则
。
根据同轴转动角速度相等,由
得
解得
设石块击中斜坡时的速度为v3,将v3分解如图所示
据几何知识得
解得
(2)据几何知识得
竖直方向上
水平方向
联立解得
20.(1)8rad/s;(2)8m/s;(3)4.16m/s
【详解】
(1)大齿轮 的最大角速度
ω1=2πn=8rad/s
(2)运动过程中自行车的最大速度
(3)到达最大速度时的位移
匀加速的时间
匀速的时间
加速和匀速阶段的平均速度
减速阶段
解得
v=4.16m/s
21.(1) ;(2),
【详解】
(1)为了保证两球相碰,球Q从A点飞出水平射程为L,设飞出时的速度为v,则有
,
A在水平面上有
,
要使两球相碰应有
联立解得
(2)由(1)可知,k=0,Q运动到槽口的时间最短,则有
最小拉力为
Q在槽上滑行的距离为x,则有
代入数据解得
22.(1)见解析;(2)48圈
【详解】
(1)通过链条相连的牙盘和飞轮边缘的线速度相同,当牙盘的半径大于飞轮的半径时,由v=ωr知,牙盘的角速度小于飞轮的角速度,即人踩脚踏板的角速度小于后轮的角速度,这样即使脚蹬得慢,自行车也能获得较快的速度;
(2)自行车行进的速度等于后轮边缘上某点绕转轴转动的线速度。设牙盘转动的角速度为ω1,自行车后轮转动的角速度,即飞轮的角速度为ω2,人踩脚踏板的转速为n,则
由于
解得
即每分钟要踩脚踏板48圈。
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第1章 功和机械能
- 导入 神奇之能
- 第1节 机械功
- 第2节 功率
- 第3节 动能和动能定理
- 第4节 势能及其改变
- 第5节 科学验证:机械能守恒定律
- 第2章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 平抛运动
- 第3节 科学探究:平抛运动的特点
- 第4节 生活中的抛体运动
- 第3章 圆周运动
- 导入 生活中的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 科学探究:向心力
- 第3节 离心现象
- 第4章 万有引力定律及航天
- 导入 从嫦娥奔月到“阿波罗”上天
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈探索
- 第5章 科学进步无止境
- 导入 再次跨越时空的对话
- 第1节 初识相对论
- 第2节 相对论中的神奇时空
- 第3节 探索宇宙的奥秘
