青岛版九年级数学下册 5.7 二次函数的应用(第2课时)课件(14张ppt)
文档属性
| 名称 | 青岛版九年级数学下册 5.7 二次函数的应用(第2课时)课件(14张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-14 22:47:40 | ||
图片预览





文档简介
(共17张PPT)
5.7 二次函数的应用
第2课时
1、复习巩固利用二次函数解决实际问题的方法、步骤;
2、经历探索体育运动和财经问题最大或最小问题的过程,进一步获得利用数学方法解决实际问题的经验,感受数学模型思想和数学的应用价值;
3、通过对生活中具体实例的分析,体会数学源于生活又应用与生活的哲理.
学习目标
1、如何运用二次函数求实际问题中的最大值或最小值
2、首先应当求出函数解析式和自变量的取值范围,然后通过配方变形,或利用公式求它的最大值或最小值.
注意:通过函数关系式求得的最大值或最小值对应的自变量的值必须在实际问题自变量的取值范围内.
设、列、解、验、答
知识回顾
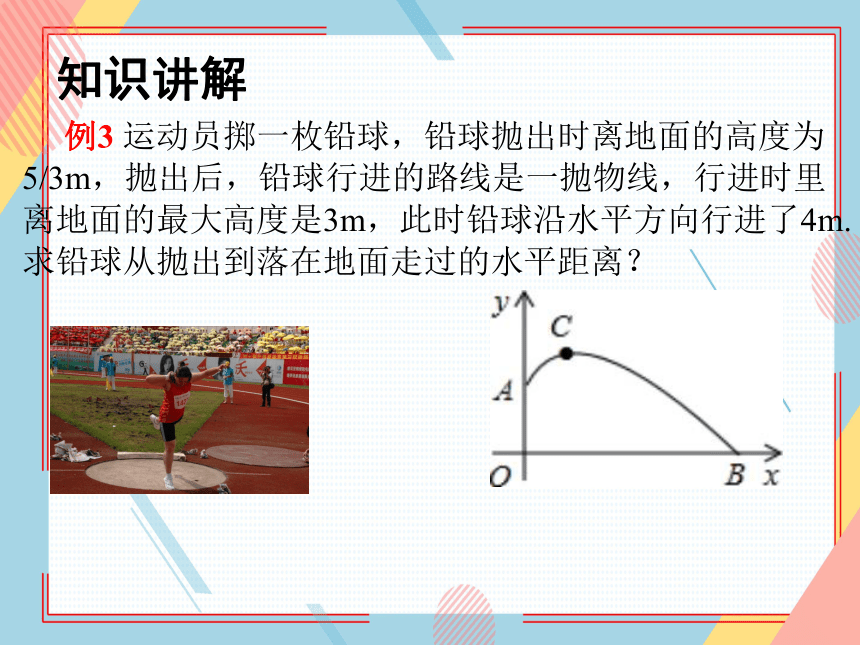
例3 运动员掷一枚铅球,铅球抛出时离地面的高度为5/3m,抛出后,铅球行进的路线是一抛物线,行进时里离地面的最大高度是3m,此时铅球沿水平方向行进了4m.求铅球从抛出到落在地面走过的水平距离?
知识讲解
解:以铅球出手点A所在铅垂线为y轴,铅垂线与地面的交点为O点,射线OA的方向为y轴正方向.铅球的落地点为B点,直线OB为x轴,射线OB的方向为x轴的正方向,x轴,y轴均匀1m为单位长度,建立如图所示的直角坐标系.由题意可知,抛物线的顶点C的坐标是(4,3).
设抛物的表达式为:y=a(x-4) +3.
由题意知,当x=0时,y=5/3,
所以5/3=a(0-4) +3,解得a=-1/12.
所以,抛物线的表达式为:y=-1/12(x-4) +3.
令y=0,得-1/12(x-4) +3=0.
解之得 x1=-2,x2=10
代入实际问题中检验,x1=-2(m)不符合题意,舍去;x2=10符合题意.
所以,铅球从抛出到落地走过的水平距离为10m.
4
3
1、恰当的建立平面直角坐标系,构造出符合题意的二次函数(一次函数、反比例函数)是解决此类问题的关键.
2、此类问题进一步体现了数学建模思想方法的应用,同学们要认真掌握!
归纳总结
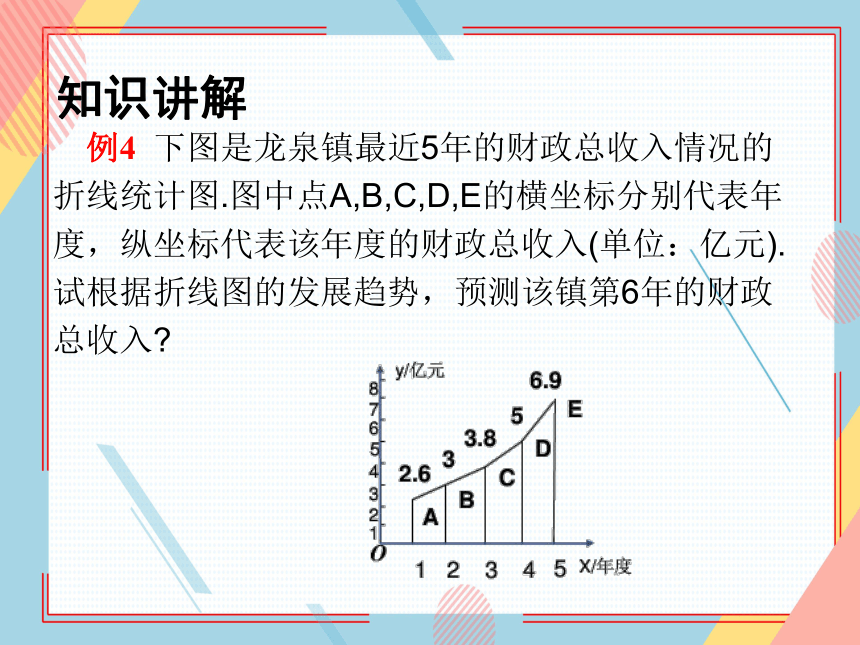
例4 下图是龙泉镇最近5年的财政总收入情况的折线统计图.图中点A,B,C,D,E的横坐标分别代表年度,纵坐标代表该年度的财政总收入(单位:亿元).试根据折线图的发展趋势,预测该镇第6年的财政总收入
知识讲解
方法点拨
由上图可以看出A,B,C,D,E近似的分布在一条抛物线上,因此可以选取其中的三个点,求出有这三个点确定的抛物线的解析式,然后验证其他各点是否也靠近这条抛物线,如果靠近,便可推测第6年的财政总收入也符合以上规律.从而可以预测第6年的财政总收入.
解得 a=0.2
b=-0.2
c=2.6
解:设图像过A,C,D三点的二次函数表达式为y=ax +bx+c.将这三点的坐标(1,2.6)(3,3.8)(4,5)分别代入上式,得
2.6=a×1 +b×1+c
3.8=a×3 +b×3+c
5=a×4 +b×4+c
所以,经过A,C,D三点的二次函数的表达式为 y=0.2x -0.2x+2.6
由此可知,二次函数y=0.2x -0.2x+2.6可以近似的反映该镇最近5年的财政收入情况发展趋势,因此可以利用前5年的发展趋势预测第6年的财政收入.
当x=2时,代入y=0.2x -0.2x+2.6,得y=3,与B点纵坐标相等,这说明点B在经过A,C,D三点的二次函数的图像上,即这条抛物线上相应的点的纵坐标反映了该镇第2年的财政收入.
当x=5时,代入y=0.2x -0.2x+2.6,得y=6.6,E点纵坐标为6.9,相差0.3(亿元),这说明点E虽不在经过A,C,D三点的抛物线上,但比较接近,即这条抛物线上相应的点的纵坐标可以近似的反映该镇第5年的财政收入.
当x=6时,代入y=0.2x -0.2x+2.6,得x=8.6,所以,可以预测2010年该镇的财政收入约为8.6亿元.
将若干小正方形按右图排列,自上而下、自左而右填入正整数1,2,3,4,……按这规律,继续做下去,再把其中奇数行的中间的小正方形用粗线条描出,则这些小正方形的序号及小正方形中的数字组成一个整数对序列:
(1,1),(2,5),(3,13)……
(1)写出这个序列中的第4,5,6个数对
(2)将这些数对在直角坐标系中描出
(3)你猜测这些点分布在一条什么样的曲线上?你能验证你的猜测是正确的吗?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(4,25),(5,41),(6,61)
y= 2x -2x+1 (x是正整数)
描点略
挑战自我
运用二次函数的性质求实际问题的最大值和最小值的一般步骤 :
1、求出函数解析式和自变量的取值范围.
2、配方变形,或利用公式求它的最大值或最小值.
3、检查求得的最大值或最小值对应的字变量的值必须在自变量的取值范围内 .
本课小结
必做题:习题5.7 5题
选做题:习题5.7 4题
随堂练习
龙泉饮料销售部每天的固定成本为500元,其销售的饮料每瓶进价为5元.销售单价与日均销售量的关系如下:
①若记销售单价比每瓶进价多x元,日均毛利润(毛利润=售价-进价-固定成本)为y元,求y 关于x的函数解析式和自变量的取值范围;
②若要使日均毛利润达到最大,销售单价应定为多
少元(精确到0.1元)?最大日均毛利润为多
少元?
销售单价(元) 6 7 8 9 10 11 12
日均销售量(瓶) 480 440 400 360 320 280 240
课下练习
5.7 二次函数的应用
第2课时
1、复习巩固利用二次函数解决实际问题的方法、步骤;
2、经历探索体育运动和财经问题最大或最小问题的过程,进一步获得利用数学方法解决实际问题的经验,感受数学模型思想和数学的应用价值;
3、通过对生活中具体实例的分析,体会数学源于生活又应用与生活的哲理.
学习目标
1、如何运用二次函数求实际问题中的最大值或最小值
2、首先应当求出函数解析式和自变量的取值范围,然后通过配方变形,或利用公式求它的最大值或最小值.
注意:通过函数关系式求得的最大值或最小值对应的自变量的值必须在实际问题自变量的取值范围内.
设、列、解、验、答
知识回顾
例3 运动员掷一枚铅球,铅球抛出时离地面的高度为5/3m,抛出后,铅球行进的路线是一抛物线,行进时里离地面的最大高度是3m,此时铅球沿水平方向行进了4m.求铅球从抛出到落在地面走过的水平距离?
知识讲解
解:以铅球出手点A所在铅垂线为y轴,铅垂线与地面的交点为O点,射线OA的方向为y轴正方向.铅球的落地点为B点,直线OB为x轴,射线OB的方向为x轴的正方向,x轴,y轴均匀1m为单位长度,建立如图所示的直角坐标系.由题意可知,抛物线的顶点C的坐标是(4,3).
设抛物的表达式为:y=a(x-4) +3.
由题意知,当x=0时,y=5/3,
所以5/3=a(0-4) +3,解得a=-1/12.
所以,抛物线的表达式为:y=-1/12(x-4) +3.
令y=0,得-1/12(x-4) +3=0.
解之得 x1=-2,x2=10
代入实际问题中检验,x1=-2(m)不符合题意,舍去;x2=10符合题意.
所以,铅球从抛出到落地走过的水平距离为10m.
4
3
1、恰当的建立平面直角坐标系,构造出符合题意的二次函数(一次函数、反比例函数)是解决此类问题的关键.
2、此类问题进一步体现了数学建模思想方法的应用,同学们要认真掌握!
归纳总结
例4 下图是龙泉镇最近5年的财政总收入情况的折线统计图.图中点A,B,C,D,E的横坐标分别代表年度,纵坐标代表该年度的财政总收入(单位:亿元).试根据折线图的发展趋势,预测该镇第6年的财政总收入
知识讲解
方法点拨
由上图可以看出A,B,C,D,E近似的分布在一条抛物线上,因此可以选取其中的三个点,求出有这三个点确定的抛物线的解析式,然后验证其他各点是否也靠近这条抛物线,如果靠近,便可推测第6年的财政总收入也符合以上规律.从而可以预测第6年的财政总收入.
解得 a=0.2
b=-0.2
c=2.6
解:设图像过A,C,D三点的二次函数表达式为y=ax +bx+c.将这三点的坐标(1,2.6)(3,3.8)(4,5)分别代入上式,得
2.6=a×1 +b×1+c
3.8=a×3 +b×3+c
5=a×4 +b×4+c
所以,经过A,C,D三点的二次函数的表达式为 y=0.2x -0.2x+2.6
由此可知,二次函数y=0.2x -0.2x+2.6可以近似的反映该镇最近5年的财政收入情况发展趋势,因此可以利用前5年的发展趋势预测第6年的财政收入.
当x=2时,代入y=0.2x -0.2x+2.6,得y=3,与B点纵坐标相等,这说明点B在经过A,C,D三点的二次函数的图像上,即这条抛物线上相应的点的纵坐标反映了该镇第2年的财政收入.
当x=5时,代入y=0.2x -0.2x+2.6,得y=6.6,E点纵坐标为6.9,相差0.3(亿元),这说明点E虽不在经过A,C,D三点的抛物线上,但比较接近,即这条抛物线上相应的点的纵坐标可以近似的反映该镇第5年的财政收入.
当x=6时,代入y=0.2x -0.2x+2.6,得x=8.6,所以,可以预测2010年该镇的财政收入约为8.6亿元.
将若干小正方形按右图排列,自上而下、自左而右填入正整数1,2,3,4,……按这规律,继续做下去,再把其中奇数行的中间的小正方形用粗线条描出,则这些小正方形的序号及小正方形中的数字组成一个整数对序列:
(1,1),(2,5),(3,13)……
(1)写出这个序列中的第4,5,6个数对
(2)将这些数对在直角坐标系中描出
(3)你猜测这些点分布在一条什么样的曲线上?你能验证你的猜测是正确的吗?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(4,25),(5,41),(6,61)
y= 2x -2x+1 (x是正整数)
描点略
挑战自我
运用二次函数的性质求实际问题的最大值和最小值的一般步骤 :
1、求出函数解析式和自变量的取值范围.
2、配方变形,或利用公式求它的最大值或最小值.
3、检查求得的最大值或最小值对应的字变量的值必须在自变量的取值范围内 .
本课小结
必做题:习题5.7 5题
选做题:习题5.7 4题
随堂练习
龙泉饮料销售部每天的固定成本为500元,其销售的饮料每瓶进价为5元.销售单价与日均销售量的关系如下:
①若记销售单价比每瓶进价多x元,日均毛利润(毛利润=售价-进价-固定成本)为y元,求y 关于x的函数解析式和自变量的取值范围;
②若要使日均毛利润达到最大,销售单价应定为多
少元(精确到0.1元)?最大日均毛利润为多
少元?
销售单价(元) 6 7 8 9 10 11 12
日均销售量(瓶) 480 440 400 360 320 280 240
课下练习
