1.3.4《算法案例(进位制)》(下)
文档属性
| 名称 | 1.3.4《算法案例(进位制)》(下) |  | |
| 格式 | zip | ||
| 文件大小 | 943.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-21 18:13:09 | ||
图片预览







文档简介
课件23张PPT。1.3.4《算法案例(进位制)》(下) 湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作问题提出 1.“满几进一”就是几进制,k进制使用哪几个数字,k进制数化为十进制数的一般算式是什么? 2.利用k进制数化十进制数的一般算式,可以构造算法,设计程序,通过计算机就能把任何一个k进制数化为十进制数.在实际应用中,我们还需要把任意一个十进制数化为k进制数的算法,对此,我们作些理论上的探讨.例1:把89化为二进制的数. 分析:把89化为二进制的数,需想办法将89先写成如下形式89=an×2n+an-1×2n-1+…+a1×21+a0×20 .89=64+16+8+1=1×26+0×25+1×24 +1×23+0×22+0×21+1×20
=1011001(2).但如果数太大,我们是无法这样凑出来的,怎么办?89=44×2+1, 44=22×2+0, 22=11×2+0, 11=5×2+1, 5=2×2+1, 2=1×2+0, 1=0×2+1, 89=44×2+1, 44=22×2+0, 22=11×2+0, 11=5×2+1, 5=2×2+1, 89=44×2+1,
=(22×2+0)×2+1
=((11×2+0)×2+0)×2+1
=(((5×2+1)×2+0)×2+0)×2+1
=((((2×2+1)×2+1)×2+0)× 2+0)×2+1
=(((((1×2)+0)×2+1)×2+1)×2+0)× 2+0)×2+1=1×26+0×25+1×24 +1×23+0×22+0×21+1×20=1011001(2).可以用2连续去除89或所得商(一直到商为0为止),然后取余数
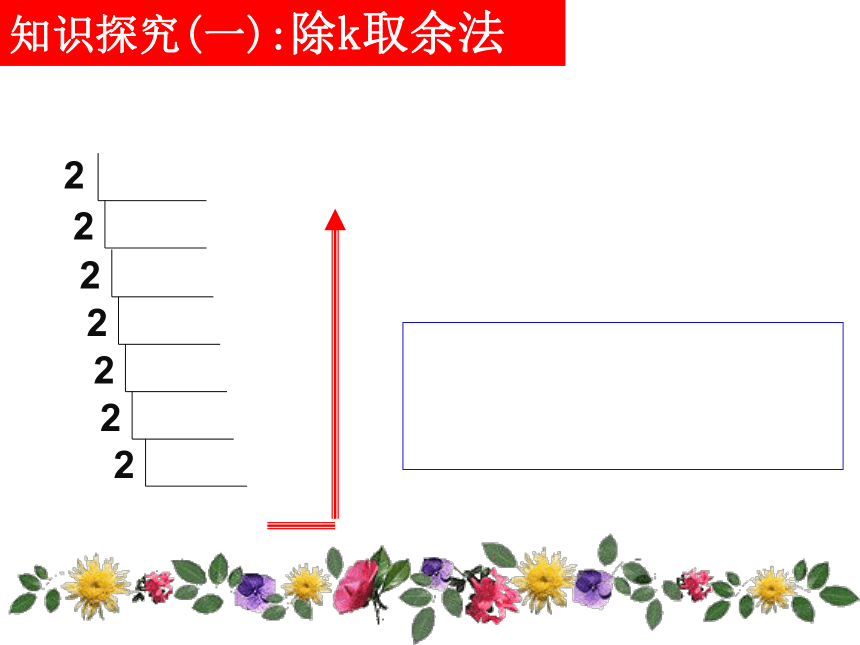
---除2取余法.2=1×2+0, 1=0×2+1, 44 1我们可以用下面的除法算式表示除2取余法:22 011 05 12 11 00 1把算式中各步所得的余数从下到上排列,得到89=1011001(2).这种方法也可以推广为把十进制数化为k进制数的算法,称为除k取余法.知识探究(一):除k取余法练习:十进制数191化为五进制数是什么数?191=1231(5)思考:若十进制数 a除以2所得的商是q0,余数是r0, 即a=2·q0+ r0;
q0除以2所得的商是q1,余数是r1, 即q0=2·q1+ r1;
……
qn-1除以2所得的商是0,余数是rn, 即qn-1= rn,
那么十进制数a化为二进制数是什么数?a=rnrn-1…r1r0(2)知识探究(二):十进制化k进制的算法 思考1:根据上面的分析,将十进制数a化为二进制数的算法步骤如何设计?第四步,若q≠0,则a=q,返回第二步; 否则,输出全部余数r排列得到 的二进制数.第一步,输入十进制数a的值.第二步,求出a除以2所得的商q,余数r.第三步,把所得的余数依次从右到左排列.思考2:利用除k取余法,将十进制数a化为k进制数的算法步骤如何设计?第四步,若q≠0,则a=q,返回第二步; 否则,输出全部余数r排列得到 的k进制数.第一步,输入十进制数a和基数k的值.第二步,求出a除以k所得的商q,余数r.第三步,把所得的余数依次从右到左排 列.思考3:将除k取余法的算法步骤用程序框图如何表示?思考4:该程序框图对应的程序如何表述?INPUT a,kb=0i=0DOq=a/kr=a MOD kb=b+r*10∧ii=i+1a=qLOOP UNTIL q=0PRINT bEND将k进制数a转换为十进制数(共有 n位)的程序a=anan-1… a3a2a1(k) =ank(n-1)+an-1k(n-2)+ … + a3k2 +a2k1+a1k0b=a1k0b=a2k1 +bb=a3k2 + b…b=ankn-1 +bai=GET a[i]
GET函数用于取出a的右数第i位数INPUT a,k,ni=1b=0WHILE i<=nt=GET a[i]b=t*k^(i-1)+bi=i+1WENDPRINT bENDi=i+1i=1b=aiki-1+b附: 十进制小数转换为其他进制。转换方法:分为整数部分和小数部分,分别转换后合并。例:215.6875D ?B215.6875D=110101111.1011B十进制数转换为K进制数整数的转换可采用除K取余法,即把要转换的十进制数的整数部分不断除以K,并记下每次除所得余数,直到商为0为止,将所得余数,从最后一次除得余数读起,就是这个十进制整数所对应的K进制整数。
小数部分的转换采用乘K取整法,被转换的小数部分,每次与K相乘后,所得乘积的整数部分就为对应的K进制数,将所得小数从第一次乘得整数读起,就是这个十进制小数所对应的K进制小数。
课堂小结 1.利用除k取余法,可以把任何一个十进制数化为k进制数,并且操作简单、实用. 2.通过k进制数与十进制数的转化,我们也可以将一个k进制数转化为另一个不同基数的k进制数.课堂小结作业:
P45练习:3.
P48习题1.3A组:3(2),(4).课件23张PPT。1.3.4《算法案例(进位制)》(下) 湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作问题提出 1.“满几进一”就是几进制,k进制使用哪几个数字,k进制数化为十进制数的一般算式是什么? 2.利用k进制数化十进制数的一般算式,可以构造算法,设计程序,通过计算机就能把任何一个k进制数化为十进制数.在实际应用中,我们还需要把任意一个十进制数化为k进制数的算法,对此,我们作些理论上的探讨.例1:把89化为二进制的数. 分析:把89化为二进制的数,需想办法将89先写成如下形式89=an×2n+an-1×2n-1+…+a1×21+a0×20 .89=64+16+8+1=1×26+0×25+1×24 +1×23+0×22+0×21+1×20
=1011001(2).但如果数太大,我们是无法这样凑出来的,怎么办?89=44×2+1, 44=22×2+0, 22=11×2+0, 11=5×2+1, 5=2×2+1, 2=1×2+0, 1=0×2+1, 89=44×2+1, 44=22×2+0, 22=11×2+0, 11=5×2+1, 5=2×2+1, 89=44×2+1,
=(22×2+0)×2+1
=((11×2+0)×2+0)×2+1
=(((5×2+1)×2+0)×2+0)×2+1
=((((2×2+1)×2+1)×2+0)× 2+0)×2+1
=(((((1×2)+0)×2+1)×2+1)×2+0)× 2+0)×2+1=1×26+0×25+1×24 +1×23+0×22+0×21+1×20=1011001(2).可以用2连续去除89或所得商(一直到商为0为止),然后取余数
---除2取余法.2=1×2+0, 1=0×2+1, 44 1我们可以用下面的除法算式表示除2取余法:22 011 05 12 11 00 1把算式中各步所得的余数从下到上排列,得到89=1011001(2).这种方法也可以推广为把十进制数化为k进制数的算法,称为除k取余法.知识探究(一):除k取余法练习:十进制数191化为五进制数是什么数?191=1231(5)思考:若十进制数 a除以2所得的商是q0,余数是r0, 即a=2·q0+ r0;
q0除以2所得的商是q1,余数是r1, 即q0=2·q1+ r1;
……
qn-1除以2所得的商是0,余数是rn, 即qn-1= rn,
那么十进制数a化为二进制数是什么数?a=rnrn-1…r1r0(2)知识探究(二):十进制化k进制的算法 思考1:根据上面的分析,将十进制数a化为二进制数的算法步骤如何设计?第四步,若q≠0,则a=q,返回第二步; 否则,输出全部余数r排列得到 的二进制数.第一步,输入十进制数a的值.第二步,求出a除以2所得的商q,余数r.第三步,把所得的余数依次从右到左排列.思考2:利用除k取余法,将十进制数a化为k进制数的算法步骤如何设计?第四步,若q≠0,则a=q,返回第二步; 否则,输出全部余数r排列得到 的k进制数.第一步,输入十进制数a和基数k的值.第二步,求出a除以k所得的商q,余数r.第三步,把所得的余数依次从右到左排 列.思考3:将除k取余法的算法步骤用程序框图如何表示?思考4:该程序框图对应的程序如何表述?INPUT a,kb=0i=0DOq=a/kr=a MOD kb=b+r*10∧ii=i+1a=qLOOP UNTIL q=0PRINT bEND将k进制数a转换为十进制数(共有 n位)的程序a=anan-1… a3a2a1(k) =ank(n-1)+an-1k(n-2)+ … + a3k2 +a2k1+a1k0b=a1k0b=a2k1 +bb=a3k2 + b…b=ankn-1 +bai=GET a[i]
GET函数用于取出a的右数第i位数INPUT a,k,ni=1b=0WHILE i<=nt=GET a[i]b=t*k^(i-1)+bi=i+1WENDPRINT bENDi=i+1i=1b=aiki-1+b附: 十进制小数转换为其他进制。转换方法:分为整数部分和小数部分,分别转换后合并。例:215.6875D ?B215.6875D=110101111.1011B十进制数转换为K进制数整数的转换可采用除K取余法,即把要转换的十进制数的整数部分不断除以K,并记下每次除所得余数,直到商为0为止,将所得余数,从最后一次除得余数读起,就是这个十进制整数所对应的K进制整数。
小数部分的转换采用乘K取整法,被转换的小数部分,每次与K相乘后,所得乘积的整数部分就为对应的K进制数,将所得小数从第一次乘得整数读起,就是这个十进制小数所对应的K进制小数。
课堂小结 1.利用除k取余法,可以把任何一个十进制数化为k进制数,并且操作简单、实用. 2.通过k进制数与十进制数的转化,我们也可以将一个k进制数转化为另一个不同基数的k进制数.课堂小结作业:
P45练习:3.
P48习题1.3A组:3(2),(4).
高中数学老师欧阳文丰制作问题提出 1.“满几进一”就是几进制,k进制使用哪几个数字,k进制数化为十进制数的一般算式是什么? 2.利用k进制数化十进制数的一般算式,可以构造算法,设计程序,通过计算机就能把任何一个k进制数化为十进制数.在实际应用中,我们还需要把任意一个十进制数化为k进制数的算法,对此,我们作些理论上的探讨.例1:把89化为二进制的数. 分析:把89化为二进制的数,需想办法将89先写成如下形式89=an×2n+an-1×2n-1+…+a1×21+a0×20 .89=64+16+8+1=1×26+0×25+1×24 +1×23+0×22+0×21+1×20
=1011001(2).但如果数太大,我们是无法这样凑出来的,怎么办?89=44×2+1, 44=22×2+0, 22=11×2+0, 11=5×2+1, 5=2×2+1, 2=1×2+0, 1=0×2+1, 89=44×2+1, 44=22×2+0, 22=11×2+0, 11=5×2+1, 5=2×2+1, 89=44×2+1,
=(22×2+0)×2+1
=((11×2+0)×2+0)×2+1
=(((5×2+1)×2+0)×2+0)×2+1
=((((2×2+1)×2+1)×2+0)× 2+0)×2+1
=(((((1×2)+0)×2+1)×2+1)×2+0)× 2+0)×2+1=1×26+0×25+1×24 +1×23+0×22+0×21+1×20=1011001(2).可以用2连续去除89或所得商(一直到商为0为止),然后取余数
---除2取余法.2=1×2+0, 1=0×2+1, 44 1我们可以用下面的除法算式表示除2取余法:22 011 05 12 11 00 1把算式中各步所得的余数从下到上排列,得到89=1011001(2).这种方法也可以推广为把十进制数化为k进制数的算法,称为除k取余法.知识探究(一):除k取余法练习:十进制数191化为五进制数是什么数?191=1231(5)思考:若十进制数 a除以2所得的商是q0,余数是r0, 即a=2·q0+ r0;
q0除以2所得的商是q1,余数是r1, 即q0=2·q1+ r1;
……
qn-1除以2所得的商是0,余数是rn, 即qn-1= rn,
那么十进制数a化为二进制数是什么数?a=rnrn-1…r1r0(2)知识探究(二):十进制化k进制的算法 思考1:根据上面的分析,将十进制数a化为二进制数的算法步骤如何设计?第四步,若q≠0,则a=q,返回第二步; 否则,输出全部余数r排列得到 的二进制数.第一步,输入十进制数a的值.第二步,求出a除以2所得的商q,余数r.第三步,把所得的余数依次从右到左排列.思考2:利用除k取余法,将十进制数a化为k进制数的算法步骤如何设计?第四步,若q≠0,则a=q,返回第二步; 否则,输出全部余数r排列得到 的k进制数.第一步,输入十进制数a和基数k的值.第二步,求出a除以k所得的商q,余数r.第三步,把所得的余数依次从右到左排 列.思考3:将除k取余法的算法步骤用程序框图如何表示?思考4:该程序框图对应的程序如何表述?INPUT a,kb=0i=0DOq=a/kr=a MOD kb=b+r*10∧ii=i+1a=qLOOP UNTIL q=0PRINT bEND将k进制数a转换为十进制数(共有 n位)的程序a=anan-1… a3a2a1(k) =ank(n-1)+an-1k(n-2)+ … + a3k2 +a2k1+a1k0b=a1k0b=a2k1 +bb=a3k2 + b…b=ankn-1 +bai=GET a[i]
GET函数用于取出a的右数第i位数INPUT a,k,ni=1b=0WHILE i<=nt=GET a[i]b=t*k^(i-1)+bi=i+1WENDPRINT bENDi=i+1i=1b=aiki-1+b附: 十进制小数转换为其他进制。转换方法:分为整数部分和小数部分,分别转换后合并。例:215.6875D ?B215.6875D=110101111.1011B十进制数转换为K进制数整数的转换可采用除K取余法,即把要转换的十进制数的整数部分不断除以K,并记下每次除所得余数,直到商为0为止,将所得余数,从最后一次除得余数读起,就是这个十进制整数所对应的K进制整数。
小数部分的转换采用乘K取整法,被转换的小数部分,每次与K相乘后,所得乘积的整数部分就为对应的K进制数,将所得小数从第一次乘得整数读起,就是这个十进制小数所对应的K进制小数。
课堂小结 1.利用除k取余法,可以把任何一个十进制数化为k进制数,并且操作简单、实用. 2.通过k进制数与十进制数的转化,我们也可以将一个k进制数转化为另一个不同基数的k进制数.课堂小结作业:
P45练习:3.
P48习题1.3A组:3(2),(4).课件23张PPT。1.3.4《算法案例(进位制)》(下) 湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作问题提出 1.“满几进一”就是几进制,k进制使用哪几个数字,k进制数化为十进制数的一般算式是什么? 2.利用k进制数化十进制数的一般算式,可以构造算法,设计程序,通过计算机就能把任何一个k进制数化为十进制数.在实际应用中,我们还需要把任意一个十进制数化为k进制数的算法,对此,我们作些理论上的探讨.例1:把89化为二进制的数. 分析:把89化为二进制的数,需想办法将89先写成如下形式89=an×2n+an-1×2n-1+…+a1×21+a0×20 .89=64+16+8+1=1×26+0×25+1×24 +1×23+0×22+0×21+1×20
=1011001(2).但如果数太大,我们是无法这样凑出来的,怎么办?89=44×2+1, 44=22×2+0, 22=11×2+0, 11=5×2+1, 5=2×2+1, 2=1×2+0, 1=0×2+1, 89=44×2+1, 44=22×2+0, 22=11×2+0, 11=5×2+1, 5=2×2+1, 89=44×2+1,
=(22×2+0)×2+1
=((11×2+0)×2+0)×2+1
=(((5×2+1)×2+0)×2+0)×2+1
=((((2×2+1)×2+1)×2+0)× 2+0)×2+1
=(((((1×2)+0)×2+1)×2+1)×2+0)× 2+0)×2+1=1×26+0×25+1×24 +1×23+0×22+0×21+1×20=1011001(2).可以用2连续去除89或所得商(一直到商为0为止),然后取余数
---除2取余法.2=1×2+0, 1=0×2+1, 44 1我们可以用下面的除法算式表示除2取余法:22 011 05 12 11 00 1把算式中各步所得的余数从下到上排列,得到89=1011001(2).这种方法也可以推广为把十进制数化为k进制数的算法,称为除k取余法.知识探究(一):除k取余法练习:十进制数191化为五进制数是什么数?191=1231(5)思考:若十进制数 a除以2所得的商是q0,余数是r0, 即a=2·q0+ r0;
q0除以2所得的商是q1,余数是r1, 即q0=2·q1+ r1;
……
qn-1除以2所得的商是0,余数是rn, 即qn-1= rn,
那么十进制数a化为二进制数是什么数?a=rnrn-1…r1r0(2)知识探究(二):十进制化k进制的算法 思考1:根据上面的分析,将十进制数a化为二进制数的算法步骤如何设计?第四步,若q≠0,则a=q,返回第二步; 否则,输出全部余数r排列得到 的二进制数.第一步,输入十进制数a的值.第二步,求出a除以2所得的商q,余数r.第三步,把所得的余数依次从右到左排列.思考2:利用除k取余法,将十进制数a化为k进制数的算法步骤如何设计?第四步,若q≠0,则a=q,返回第二步; 否则,输出全部余数r排列得到 的k进制数.第一步,输入十进制数a和基数k的值.第二步,求出a除以k所得的商q,余数r.第三步,把所得的余数依次从右到左排 列.思考3:将除k取余法的算法步骤用程序框图如何表示?思考4:该程序框图对应的程序如何表述?INPUT a,kb=0i=0DOq=a/kr=a MOD kb=b+r*10∧ii=i+1a=qLOOP UNTIL q=0PRINT bEND将k进制数a转换为十进制数(共有 n位)的程序a=anan-1… a3a2a1(k) =ank(n-1)+an-1k(n-2)+ … + a3k2 +a2k1+a1k0b=a1k0b=a2k1 +bb=a3k2 + b…b=ankn-1 +bai=GET a[i]
GET函数用于取出a的右数第i位数INPUT a,k,ni=1b=0WHILE i<=nt=GET a[i]b=t*k^(i-1)+bi=i+1WENDPRINT bENDi=i+1i=1b=aiki-1+b附: 十进制小数转换为其他进制。转换方法:分为整数部分和小数部分,分别转换后合并。例:215.6875D ?B215.6875D=110101111.1011B十进制数转换为K进制数整数的转换可采用除K取余法,即把要转换的十进制数的整数部分不断除以K,并记下每次除所得余数,直到商为0为止,将所得余数,从最后一次除得余数读起,就是这个十进制整数所对应的K进制整数。
小数部分的转换采用乘K取整法,被转换的小数部分,每次与K相乘后,所得乘积的整数部分就为对应的K进制数,将所得小数从第一次乘得整数读起,就是这个十进制小数所对应的K进制小数。
课堂小结 1.利用除k取余法,可以把任何一个十进制数化为k进制数,并且操作简单、实用. 2.通过k进制数与十进制数的转化,我们也可以将一个k进制数转化为另一个不同基数的k进制数.课堂小结作业:
P45练习:3.
P48习题1.3A组:3(2),(4).
