4.2数值计算课件-2021-2022学年高中信息技术教科版(2019)必修一课件(28张PPT)
文档属性
| 名称 | 4.2数值计算课件-2021-2022学年高中信息技术教科版(2019)必修一课件(28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2022-04-14 12:47:14 | ||
图片预览




文档简介
(共28张PPT)
4.2数值计算
CONTENTS
感受数据的图形化表示
01
设计解析式方程
02
设计迭代方程
03
进行数值计算
04
了解数值类算法在实际问题解决时的应用及常用方法
05
第
一
章
节
di
yi
zhang
jie
导入:数值计算
数值计算,其实是数学的一个分支,它以数字计算机求解数学问题的理论和方法为研究对象,借助计算机运算速度快、精确度高的特点来解决各种数据问题。
1.1 导入
什么是数值计算
04
函数计算
方程求解
数列求和
数值计算
=
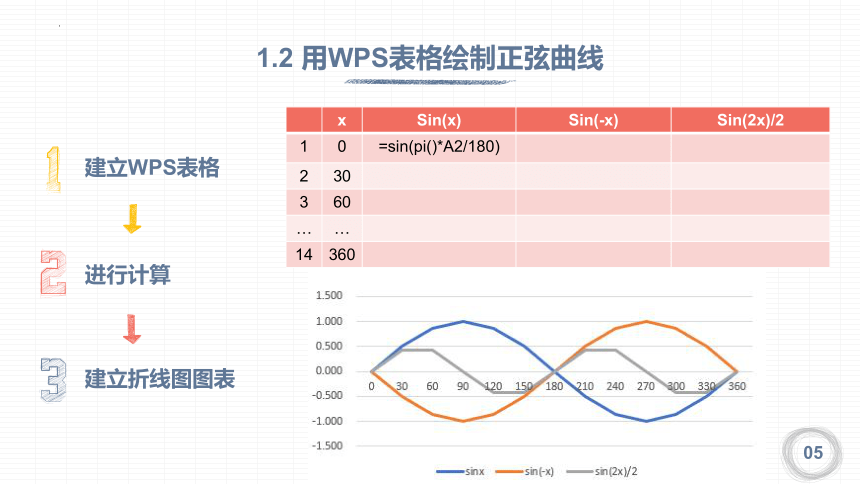
建立WPS表格
进行计算
建立折线图图表
1.2 用WPS表格绘制正弦曲线
05
x Sin(x) Sin(-x) Sin(2x)/2
1 0 =sin(pi()*A2/180)
2 30
3 60
… …
14 360
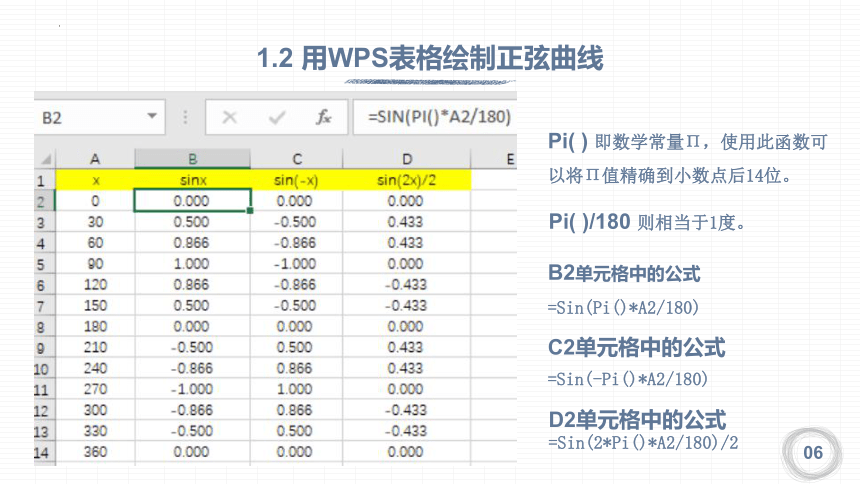
Pi( ) 即数学常量П,使用此函数可以将П值精确到小数点后14位。
1.2 用WPS表格绘制正弦曲线
06
Pi( )/180 则相当于1度。
B2单元格中的公式
=Sin(Pi()*A2/180)
C2单元格中的公式
=Sin(-Pi()*A2/180)
D2单元格中的公式
=Sin(2*Pi()*A2/180)/2
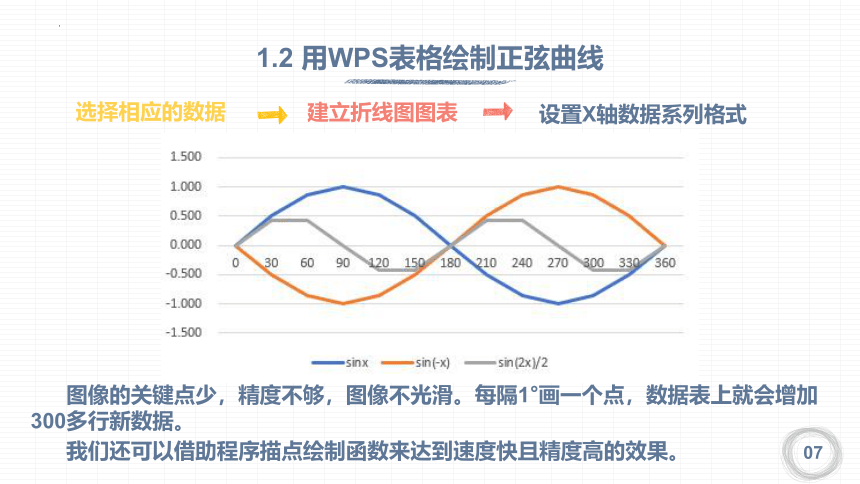
选择相应的数据
建立折线图图表
设置X轴数据系列格式
1.2 用WPS表格绘制正弦曲线
07
图像的关键点少,精度不够,图像不光滑。每隔1°画一个点,数据表上就会增加300多行新数据。
我们还可以借助程序描点绘制函数来达到速度快且精度高的效果。
1.3 利用python绘制正弦曲线
Numpy模块
Matplotlib模块
两个模块的安装
08
简介
numpy是一个科学计算包,其中包含很多数学函数,如三角函数、矩阵计算方法等。通过该模块中的arange函数可以创建一个等差数列。如在0~2П之间每隔0.01取个值,则可以用arange(0,2*numpy.pi ,0.01)来表示,其中numpy.pi表示Π。下列代码可以产生sin(x)的若干个关键点。
应用─创建三角函数图像
#加载numpy模块并取一个简洁的别名为np,便于后续引用
import numpy as np
#x在0到2Π之间,每隔0.01取一个点
x=np.arange(0 , 2*np.pi , 0.01) #调用numpy模块的arange函数,其参数为开始参数0,结束参数2*np. pi,间隔参数0.01
y=np.sin(x) #通过解析式计算列表x对应的列表y的值
1.3.1 Numpy模块
09
简介
matplotlib模块是Python中最出色的绘图库,功能很完善。调用matplotlib. pyplot时,坐标系可以根据数值范围自动生成。
matplotlib的绘图原理很简单,利用plot画线函数就可以在直角平面内轻松地将(x,y)坐标点对连接成平滑曲线。例如:在上述代码的适当位置增加下列语句,就可以将刚才生产的关键点连接起来。
应用
#加载matplotlib. pyplot并取别名为plt
import matplotlib.pyplot as plt
plt.plot(x, y) # plot()函数将点对连线
plt.show () # show()函数将绘制的图像窗口显示出来
1.3.2 Matplotlib模块
10
参考代码并补充
#加载numpy模块并取名为np
import matplotlib.pyplot as plt #加载matplotlib.pyplot并取名为plt
#x在0到2π之间,每隔0.01取一个点
#求sin(x)对应的y1值
y2=np.sin(-x) #求sin(-x)对应的y2值
#求sin(2x)/2对应的y3值
plt.plot(x,y1) #绘制sin(x)图像
#绘制sin(-x)图像
#绘制sin(2*x)/2图像
plt.title('sin(x)’) #设置图像标题
plt.xlabel('X’) #设置X轴标题
plt.ylabel('Y’) #设置Y轴标题
plt.show() #将绘制的函数图像窗口显示出来
input("运行完毕,请按回车键退出...")
1.4 Python绘制函数图像
11
完整代码
import numpy as np #加载numpy模块并取名为np
import matplotlib.pyplot as plt #加载matplotlib.pyplot并取名为plt
x=np.arange(0,2*np.pi,0.01) #x在0到2π之间,每隔0.01取一个点
y1=np.sin(x) #求sin(x)对应的y1值
y2=np.sin(-x) #求sin(-x)对应的y2值
y3=np.sin(2*x)/2 #求sin(2x)/2对应的y3值
plt.plot(x,y1) #绘制sin(x)图像
plt.plot(x,y2) #绘制sin(-x)图像
plt.plot(x,y3) #绘制sin(2*x)/2图像
plt.title('sin(x)’) #设置图像标题
plt.xlabel('X’) #设置X轴标题
plt.ylabel('Y’) #设置Y轴标题
plt.show() #将绘制的函数图像窗口显示出来
input("运行完毕,请按回车键退出...")
1.4 Python绘制函数图像
12
1.4 Python绘制函数图像
13
第
二
章
节
di
er
zhang
jie
求解斐波那契数列
2.1 斐波那契数列
故事得从西元1202年说起,话说有一位意大利青年,名叫斐波那契。在他的一部著作中提出了一个有趣的问题:假设一对刚出生的小兔一个月后就能长成大兔,再过一个月就能生下一对小兔,并且此后每个月都生一对小兔,一年内没有发生死亡,问:一对刚出生的兔子,一年内繁殖成多少对兔子
15
2.1 斐波那契数列
16
右边这一列数字是有规律的。第一个数和第二个数为1,之后的每一个数为之前两个数之和。比如,六月份的兔子数量为四月份和五月份兔子数量之和,即8=5+3。
2.1.1斐波那契数列-数学计算
17
1,
1,
1+1=2,
2+1=3,
3+2=5,
5+3=8,
8+5=13,
13+8=21,
…..
数学计算
2.1.2 斐波那契数列-WPS
18
WPS
2.1.3 斐波那契数列-Python
19
Python
第
三
章
节
di
san
zhang
jie
迭代法
3.1迭代法
每一次的重复称为一次迭代,每次迭代的结果被用作下一次的迭代值
一般用于数值计算。累加、累乘都是迭代算法的基础应用。
迭代法(辗转法)是一种不断用变量的旧值递推出新值的解决问题的方法。迭代算法是用计算机解决问题的一种基本方法。
21
确定迭代变量
建立迭代关系式
3.1迭代法
对迭代过程进行控制
22
利用迭代法来解决问题,有三个关键的步骤:
第
四
章
节
di
si
zhang
jie
扩展练习
4.1 练习一
24
尝试用python绘制y=x2-2x+1的图像
import numpy as np #加载numpy模块并取名为np
import matplotlib.pyplot as plt #加载matplotlib.pyplot并取名为plt
x=np.arange(-10,10,0.01) #x在0到2π之间,每隔0.01取一个点
y=x**2-2*x+1 #求x**2-2x+1对应的y1值
plt.plot(x,y) #绘制图像
plt.title('y=x**2-2*x+1’) #设置图像标题
plt.xlabel('X’) #设置X轴标题
plt.ylabel('Y’) #设置Y轴标题
plt.show() #将绘制的函数图像窗口显示出来
input("运行完毕,请按回车键退出...")
4.2 练习二
尝试用辗转相除法求解两个正整数的最大公约数
25
辗转相除法:用较大数除以较小数,再用出现的余数(第一余数)去除除数,再用出现的余数(第二余数)去除第一余数,如此反复,直到最后余数是0为止。如果是求两个数的最大公约数,那么最后的除数就是这两个数的最大公约数。
4.2.2练习二实现原理讲解
尝试用辗转相除法求解两个正整数的最大公约数
26
step1: 将两数中大的那个数放在m中,小的放在n中。
step2: 求出m被n除后的余数r。
step3: 若余数为0则执行步骤(7),否则执行步骤(4)。
step4: 把除数作为新的被除数;把余数作为新的除数。
step5: 求出新的余数r。
step6: 重复步骤(3)到(5)。
step7: 输出n,n即为最大公约数。
4.2.2练习二python代码实现
尝试用辗转相除法求解两个正整数的最大公约数
m,n=map(int,input("请输入两个数:").split(","))
if mm,n=n,m
r=m%n
while r:
m=n
n=r
r=m%n
print(f"最大公约数师{n}")
m,n: 先用split函数把输入用逗号分隔的两个数分离,再用map函数把分离的两个数变成整数,最后分别赋值给m和n。
if: 在后面的代码中m作为被除数,要比n大,所以如果m小于n,则交换m和n的值(Python中不用第三个变量作为中间变量,可直接用上述语句进行变量间值的交换)。
while: 如果余数不为0,则把n赋值给m,r赋值给n,算出新的余数,直到余数变为0,程序结束,得到的n即为最大公约数。
print: 打印出最大公约数。
27
THANKS
谢谢聆听
4.2数值计算
CONTENTS
感受数据的图形化表示
01
设计解析式方程
02
设计迭代方程
03
进行数值计算
04
了解数值类算法在实际问题解决时的应用及常用方法
05
第
一
章
节
di
yi
zhang
jie
导入:数值计算
数值计算,其实是数学的一个分支,它以数字计算机求解数学问题的理论和方法为研究对象,借助计算机运算速度快、精确度高的特点来解决各种数据问题。
1.1 导入
什么是数值计算
04
函数计算
方程求解
数列求和
数值计算
=
建立WPS表格
进行计算
建立折线图图表
1.2 用WPS表格绘制正弦曲线
05
x Sin(x) Sin(-x) Sin(2x)/2
1 0 =sin(pi()*A2/180)
2 30
3 60
… …
14 360
Pi( ) 即数学常量П,使用此函数可以将П值精确到小数点后14位。
1.2 用WPS表格绘制正弦曲线
06
Pi( )/180 则相当于1度。
B2单元格中的公式
=Sin(Pi()*A2/180)
C2单元格中的公式
=Sin(-Pi()*A2/180)
D2单元格中的公式
=Sin(2*Pi()*A2/180)/2
选择相应的数据
建立折线图图表
设置X轴数据系列格式
1.2 用WPS表格绘制正弦曲线
07
图像的关键点少,精度不够,图像不光滑。每隔1°画一个点,数据表上就会增加300多行新数据。
我们还可以借助程序描点绘制函数来达到速度快且精度高的效果。
1.3 利用python绘制正弦曲线
Numpy模块
Matplotlib模块
两个模块的安装
08
简介
numpy是一个科学计算包,其中包含很多数学函数,如三角函数、矩阵计算方法等。通过该模块中的arange函数可以创建一个等差数列。如在0~2П之间每隔0.01取个值,则可以用arange(0,2*numpy.pi ,0.01)来表示,其中numpy.pi表示Π。下列代码可以产生sin(x)的若干个关键点。
应用─创建三角函数图像
#加载numpy模块并取一个简洁的别名为np,便于后续引用
import numpy as np
#x在0到2Π之间,每隔0.01取一个点
x=np.arange(0 , 2*np.pi , 0.01) #调用numpy模块的arange函数,其参数为开始参数0,结束参数2*np. pi,间隔参数0.01
y=np.sin(x) #通过解析式计算列表x对应的列表y的值
1.3.1 Numpy模块
09
简介
matplotlib模块是Python中最出色的绘图库,功能很完善。调用matplotlib. pyplot时,坐标系可以根据数值范围自动生成。
matplotlib的绘图原理很简单,利用plot画线函数就可以在直角平面内轻松地将(x,y)坐标点对连接成平滑曲线。例如:在上述代码的适当位置增加下列语句,就可以将刚才生产的关键点连接起来。
应用
#加载matplotlib. pyplot并取别名为plt
import matplotlib.pyplot as plt
plt.plot(x, y) # plot()函数将点对连线
plt.show () # show()函数将绘制的图像窗口显示出来
1.3.2 Matplotlib模块
10
参考代码并补充
#加载numpy模块并取名为np
import matplotlib.pyplot as plt #加载matplotlib.pyplot并取名为plt
#x在0到2π之间,每隔0.01取一个点
#求sin(x)对应的y1值
y2=np.sin(-x) #求sin(-x)对应的y2值
#求sin(2x)/2对应的y3值
plt.plot(x,y1) #绘制sin(x)图像
#绘制sin(-x)图像
#绘制sin(2*x)/2图像
plt.title('sin(x)’) #设置图像标题
plt.xlabel('X’) #设置X轴标题
plt.ylabel('Y’) #设置Y轴标题
plt.show() #将绘制的函数图像窗口显示出来
input("运行完毕,请按回车键退出...")
1.4 Python绘制函数图像
11
完整代码
import numpy as np #加载numpy模块并取名为np
import matplotlib.pyplot as plt #加载matplotlib.pyplot并取名为plt
x=np.arange(0,2*np.pi,0.01) #x在0到2π之间,每隔0.01取一个点
y1=np.sin(x) #求sin(x)对应的y1值
y2=np.sin(-x) #求sin(-x)对应的y2值
y3=np.sin(2*x)/2 #求sin(2x)/2对应的y3值
plt.plot(x,y1) #绘制sin(x)图像
plt.plot(x,y2) #绘制sin(-x)图像
plt.plot(x,y3) #绘制sin(2*x)/2图像
plt.title('sin(x)’) #设置图像标题
plt.xlabel('X’) #设置X轴标题
plt.ylabel('Y’) #设置Y轴标题
plt.show() #将绘制的函数图像窗口显示出来
input("运行完毕,请按回车键退出...")
1.4 Python绘制函数图像
12
1.4 Python绘制函数图像
13
第
二
章
节
di
er
zhang
jie
求解斐波那契数列
2.1 斐波那契数列
故事得从西元1202年说起,话说有一位意大利青年,名叫斐波那契。在他的一部著作中提出了一个有趣的问题:假设一对刚出生的小兔一个月后就能长成大兔,再过一个月就能生下一对小兔,并且此后每个月都生一对小兔,一年内没有发生死亡,问:一对刚出生的兔子,一年内繁殖成多少对兔子
15
2.1 斐波那契数列
16
右边这一列数字是有规律的。第一个数和第二个数为1,之后的每一个数为之前两个数之和。比如,六月份的兔子数量为四月份和五月份兔子数量之和,即8=5+3。
2.1.1斐波那契数列-数学计算
17
1,
1,
1+1=2,
2+1=3,
3+2=5,
5+3=8,
8+5=13,
13+8=21,
…..
数学计算
2.1.2 斐波那契数列-WPS
18
WPS
2.1.3 斐波那契数列-Python
19
Python
第
三
章
节
di
san
zhang
jie
迭代法
3.1迭代法
每一次的重复称为一次迭代,每次迭代的结果被用作下一次的迭代值
一般用于数值计算。累加、累乘都是迭代算法的基础应用。
迭代法(辗转法)是一种不断用变量的旧值递推出新值的解决问题的方法。迭代算法是用计算机解决问题的一种基本方法。
21
确定迭代变量
建立迭代关系式
3.1迭代法
对迭代过程进行控制
22
利用迭代法来解决问题,有三个关键的步骤:
第
四
章
节
di
si
zhang
jie
扩展练习
4.1 练习一
24
尝试用python绘制y=x2-2x+1的图像
import numpy as np #加载numpy模块并取名为np
import matplotlib.pyplot as plt #加载matplotlib.pyplot并取名为plt
x=np.arange(-10,10,0.01) #x在0到2π之间,每隔0.01取一个点
y=x**2-2*x+1 #求x**2-2x+1对应的y1值
plt.plot(x,y) #绘制图像
plt.title('y=x**2-2*x+1’) #设置图像标题
plt.xlabel('X’) #设置X轴标题
plt.ylabel('Y’) #设置Y轴标题
plt.show() #将绘制的函数图像窗口显示出来
input("运行完毕,请按回车键退出...")
4.2 练习二
尝试用辗转相除法求解两个正整数的最大公约数
25
辗转相除法:用较大数除以较小数,再用出现的余数(第一余数)去除除数,再用出现的余数(第二余数)去除第一余数,如此反复,直到最后余数是0为止。如果是求两个数的最大公约数,那么最后的除数就是这两个数的最大公约数。
4.2.2练习二实现原理讲解
尝试用辗转相除法求解两个正整数的最大公约数
26
step1: 将两数中大的那个数放在m中,小的放在n中。
step2: 求出m被n除后的余数r。
step3: 若余数为0则执行步骤(7),否则执行步骤(4)。
step4: 把除数作为新的被除数;把余数作为新的除数。
step5: 求出新的余数r。
step6: 重复步骤(3)到(5)。
step7: 输出n,n即为最大公约数。
4.2.2练习二python代码实现
尝试用辗转相除法求解两个正整数的最大公约数
m,n=map(int,input("请输入两个数:").split(","))
if m
r=m%n
while r:
m=n
n=r
r=m%n
print(f"最大公约数师{n}")
m,n: 先用split函数把输入用逗号分隔的两个数分离,再用map函数把分离的两个数变成整数,最后分别赋值给m和n。
if: 在后面的代码中m作为被除数,要比n大,所以如果m小于n,则交换m和n的值(Python中不用第三个变量作为中间变量,可直接用上述语句进行变量间值的交换)。
while: 如果余数不为0,则把n赋值给m,r赋值给n,算出新的余数,直到余数变为0,程序结束,得到的n即为最大公约数。
print: 打印出最大公约数。
27
THANKS
谢谢聆听
