8.1.1向量数量积的概念课件-2021-2022学年高一下学期数学人教B版(2019)必修第三册(20张PPT)
文档属性
| 名称 | 8.1.1向量数量积的概念课件-2021-2022学年高一下学期数学人教B版(2019)必修第三册(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 592.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-15 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
8.1.1 向量数量积的概念
望庐山瀑布
唐.李白
日照香炉生紫烟,
遥看瀑布挂前川。
飞流直下三千尺,
疑是银河落九天。
古诗中的向量问题
本节课的知识目标:
1、通过物理中“功”等实例,理解平面向量数量积
的含义及其物理意义;
2、体会平面向量的数量积与向量投影的关系;
3、掌握数量积的坐标表达式,会进行平面向量数量积
的运算;
4、能运用数量积表示两个向量的夹角,会用数量积
判断两个平面向量的垂直关系。
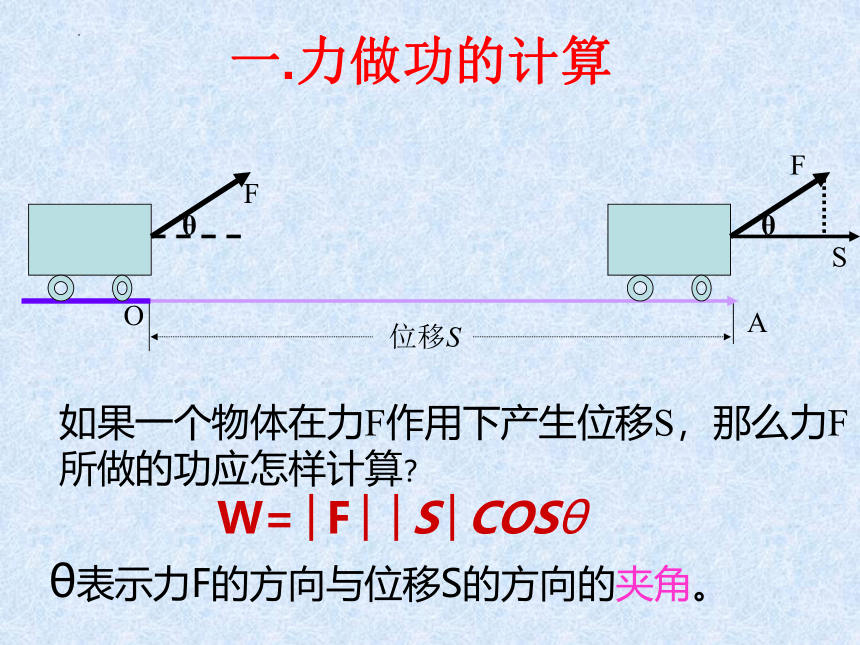
如果一个物体在力F作用下产生位移S,那么力F所做的功应怎样计算?
θ表示力F的方向与位移S的方向的夹角。
位移S
O
A
θ
F
F
θ
S
W=│F││S│COSθ
一.力做功的计算
二.两个向量的夹角
已知两个非零向量 , , ,
则∠AOB称作向量 和向量 的夹角,
记作 .
并规定
B
O
A
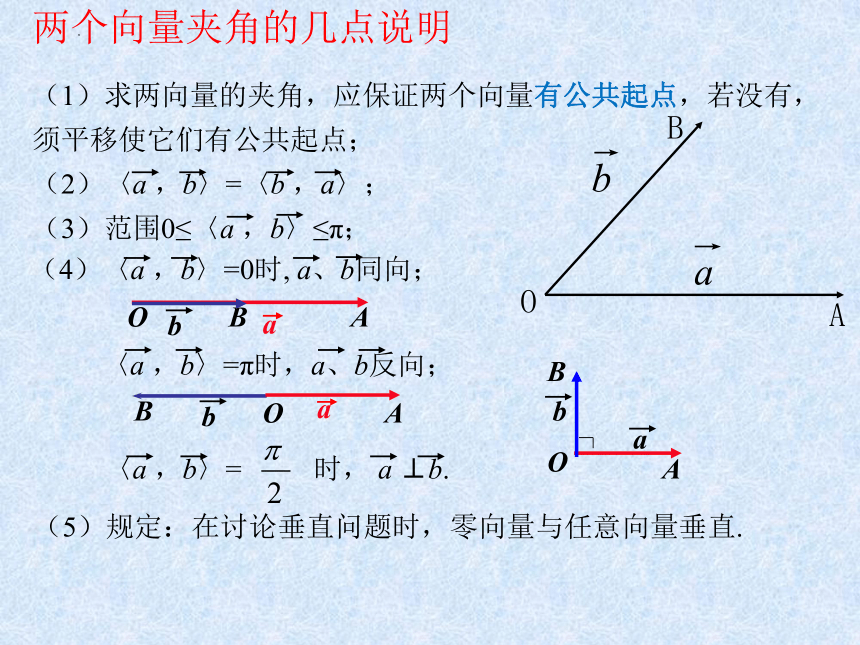
(1)求两向量的夹角,应保证两个向量有公共起点,若没有,须平移使它们有公共起点;
B
O
A
O
A
a
B
b
B
b
a
O
A
A
a
O
B
b
(2)〈a ,b〉=〈b ,a〉;
(3)范围0≤〈a ,b〉≤π;
(4)〈a ,b〉=0时, a、b同向;
〈a ,b〉=π时,a、b反向;
〈a ,b〉= 时, a ⊥b.
(5)规定:在讨论垂直问题时,零向量与任意向量垂直.
两个向量夹角的几点说明
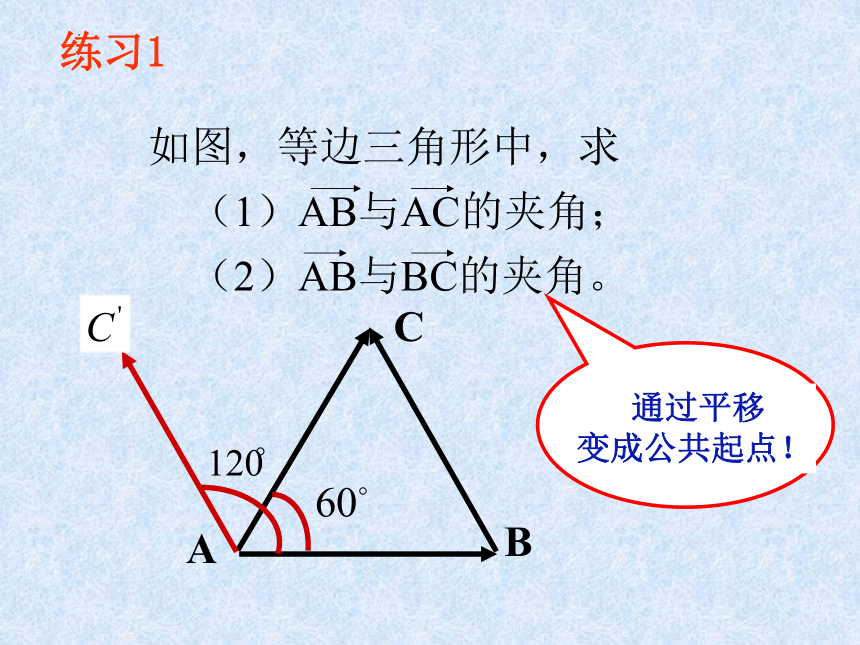
如图,等边三角形中,求
(1)AB与AC的夹角;
(2)AB与BC的夹角。
A
B
C
通过平移
变成公共起点!
练习1
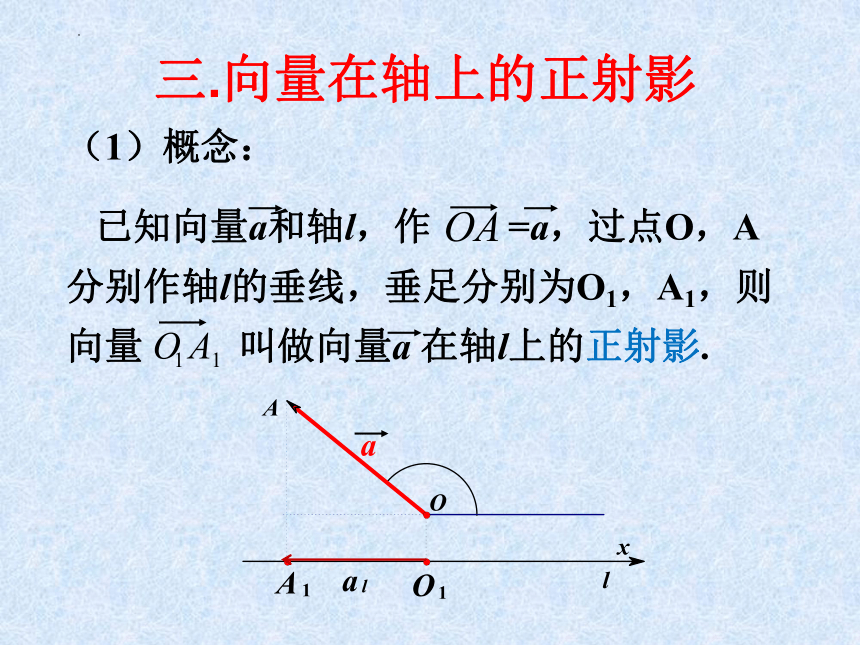
三.向量在轴上的正射影
(1)概念:
已知向量a和轴l,作 =a,过点O,A分别作轴l的垂线,垂足分别为O1,A1,则向量 叫做向量a 在轴l上的正射影.
OA
1 1
O A
(2)正射影的数量:
向量a的正射影在轴l上的坐标,称作a在轴l上的数量或在轴l方向上的数量.
记作:al
向量a的方向与轴l的正方向所成的角为θ,
则有
1. a在轴l上的数量或在轴l方向上的数量是一个数量,不是向量.
2. 当 为锐角时,数量为 ;
当 为钝角时,数量为 ;
当 为直角时,数量为 ;
当 = 0 时,数量为 ;
当 = 180 时,数量为 。
关于正射影的几点说明
a
l
x
l
O
A
2
O
1
A
1
a
l
a
a
正值
负值
0
|a|
-|a|
例1.已知轴
(1)向量 , ,求 在 上的正射影的数量OA1。
(2)向量 , ,求 在 上的正射影的数量OB1。
解:5cos600=2.5
解:OA1=5COS600=5×( )=5/2
(3)已知向量 , ,向量 , , 则向量 在向量 上的正射影的数量。
解:OB1=5COS1200=5×( - )= -5/2
四.向量的数量积(内积)
定义: 叫做向量 和 的数量积(或内积),记作:
即
1.数量积 等于 的长度与 在 方向上正射影的数量 的乘积.
关于数量积的几点说明
2.两个向量的数量积是一个实数,符号由cos〈a,b〉的符号所决定;而数乘向量是一个向量。
O
A
B
a
b
O
A
B
a
b
θ为锐角时,
| b | cosθ>0
θ为钝角时,
| b | cosθ<0
θ为直角时,
| b | cosθ=0
B
O
A
a
b
量的数量积为0
3.规定零向量与任意向
4. a · b不能写成a×b ,a×b 表示向量的另一种运算.
两个向量的数量积的性质:
设a、b为两个非零向量,e是与b的单位向量.
1. e a = a e =|a|cos ;
2. a b a b = 0
3. a a = |a|2或
4. cos = ;
5.|a b| ≤ |a|.|b|
内积为零是判定两向量垂直的条件
用于计算向量的模
用于计算向量的夹角,
以及判断三角形的形状
判断下列命题是否正确
1.若a=0,则对任意向量b,有a ·b=0.
2.若a≠0,则对任意非零向量b,有a ·b≠0.
3.若a≠0,且a · b=0,则b=0.
4.若a·b=0,则a=0或b=0.
5.对任意的向量a,有a2=│a│2.
6.若a ≠ 0,且a · b=a · c,则b=c.
( )
(×)
( )
(×)
(×)
(×)
练习2
例2.已知|a|=5,|b|=4,=120°,求a·b.
解: a b =|a|·|b|cos
=5×4×cos120°
= -10.
练习3
已知|a|=3,|b|=6,当①a∥b,②a⊥b,③a与b的夹角是60°时,分别求a·b
①a∥b时, a·b =±18;
②a⊥b时,a·b=0;
③ a与b的夹角是60°时,a·b=9.
课堂小结
1.两个向量的夹角
2.向量在轴上的正射影
正射影的数量
3.向量的数量积(内积)
a·b=
4.两个向量的数量积的性质:
(1). a b a b = 0
(2). a a = |a|2或
(3). cos =
范围0≤〈a ,b〉≤π;
作 业
完成本节课时精练内容
谢谢!
8.1.1 向量数量积的概念
望庐山瀑布
唐.李白
日照香炉生紫烟,
遥看瀑布挂前川。
飞流直下三千尺,
疑是银河落九天。
古诗中的向量问题
本节课的知识目标:
1、通过物理中“功”等实例,理解平面向量数量积
的含义及其物理意义;
2、体会平面向量的数量积与向量投影的关系;
3、掌握数量积的坐标表达式,会进行平面向量数量积
的运算;
4、能运用数量积表示两个向量的夹角,会用数量积
判断两个平面向量的垂直关系。
如果一个物体在力F作用下产生位移S,那么力F所做的功应怎样计算?
θ表示力F的方向与位移S的方向的夹角。
位移S
O
A
θ
F
F
θ
S
W=│F││S│COSθ
一.力做功的计算
二.两个向量的夹角
已知两个非零向量 , , ,
则∠AOB称作向量 和向量 的夹角,
记作 .
并规定
B
O
A
(1)求两向量的夹角,应保证两个向量有公共起点,若没有,须平移使它们有公共起点;
B
O
A
O
A
a
B
b
B
b
a
O
A
A
a
O
B
b
(2)〈a ,b〉=〈b ,a〉;
(3)范围0≤〈a ,b〉≤π;
(4)〈a ,b〉=0时, a、b同向;
〈a ,b〉=π时,a、b反向;
〈a ,b〉= 时, a ⊥b.
(5)规定:在讨论垂直问题时,零向量与任意向量垂直.
两个向量夹角的几点说明
如图,等边三角形中,求
(1)AB与AC的夹角;
(2)AB与BC的夹角。
A
B
C
通过平移
变成公共起点!
练习1
三.向量在轴上的正射影
(1)概念:
已知向量a和轴l,作 =a,过点O,A分别作轴l的垂线,垂足分别为O1,A1,则向量 叫做向量a 在轴l上的正射影.
OA
1 1
O A
(2)正射影的数量:
向量a的正射影在轴l上的坐标,称作a在轴l上的数量或在轴l方向上的数量.
记作:al
向量a的方向与轴l的正方向所成的角为θ,
则有
1. a在轴l上的数量或在轴l方向上的数量是一个数量,不是向量.
2. 当 为锐角时,数量为 ;
当 为钝角时,数量为 ;
当 为直角时,数量为 ;
当 = 0 时,数量为 ;
当 = 180 时,数量为 。
关于正射影的几点说明
a
l
x
l
O
A
2
O
1
A
1
a
l
a
a
正值
负值
0
|a|
-|a|
例1.已知轴
(1)向量 , ,求 在 上的正射影的数量OA1。
(2)向量 , ,求 在 上的正射影的数量OB1。
解:5cos600=2.5
解:OA1=5COS600=5×( )=5/2
(3)已知向量 , ,向量 , , 则向量 在向量 上的正射影的数量。
解:OB1=5COS1200=5×( - )= -5/2
四.向量的数量积(内积)
定义: 叫做向量 和 的数量积(或内积),记作:
即
1.数量积 等于 的长度与 在 方向上正射影的数量 的乘积.
关于数量积的几点说明
2.两个向量的数量积是一个实数,符号由cos〈a,b〉的符号所决定;而数乘向量是一个向量。
O
A
B
a
b
O
A
B
a
b
θ为锐角时,
| b | cosθ>0
θ为钝角时,
| b | cosθ<0
θ为直角时,
| b | cosθ=0
B
O
A
a
b
量的数量积为0
3.规定零向量与任意向
4. a · b不能写成a×b ,a×b 表示向量的另一种运算.
两个向量的数量积的性质:
设a、b为两个非零向量,e是与b的单位向量.
1. e a = a e =|a|cos ;
2. a b a b = 0
3. a a = |a|2或
4. cos = ;
5.|a b| ≤ |a|.|b|
内积为零是判定两向量垂直的条件
用于计算向量的模
用于计算向量的夹角,
以及判断三角形的形状
判断下列命题是否正确
1.若a=0,则对任意向量b,有a ·b=0.
2.若a≠0,则对任意非零向量b,有a ·b≠0.
3.若a≠0,且a · b=0,则b=0.
4.若a·b=0,则a=0或b=0.
5.对任意的向量a,有a2=│a│2.
6.若a ≠ 0,且a · b=a · c,则b=c.
( )
(×)
( )
(×)
(×)
(×)
练习2
例2.已知|a|=5,|b|=4,
解: a b =|a|·|b|cos
=5×4×cos120°
= -10.
练习3
已知|a|=3,|b|=6,当①a∥b,②a⊥b,③a与b的夹角是60°时,分别求a·b
①a∥b时, a·b =±18;
②a⊥b时,a·b=0;
③ a与b的夹角是60°时,a·b=9.
课堂小结
1.两个向量的夹角
2.向量在轴上的正射影
正射影的数量
3.向量的数量积(内积)
a·b=
4.两个向量的数量积的性质:
(1). a b a b = 0
(2). a a = |a|2或
(3). cos =
范围0≤〈a ,b〉≤π;
作 业
完成本节课时精练内容
谢谢!
