北师大版数学八年级下册 第1单元 三角形的证明 单元测试卷(含解析,PDF版)
文档属性
| 名称 | 北师大版数学八年级下册 第1单元 三角形的证明 单元测试卷(含解析,PDF版) |  | |
| 格式 | |||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-14 14:42:36 | ||
图片预览



文档简介
北师大八年级数学下册第 1 单元测试卷
一.选择题(共 10 小题,满分 30 分,每小题 3 分)
1.(3 分)等腰三角形的两边长分别为 5 和 11,则这个三角形的周长为 ( )
A.16 B.27 C.16 或 27 D.21 或 27
2.(3 分)如图,矩形 ABCD 中, AB BC ,对角线 AC 、BD相交于点O ,则图中的等腰三角形有
( )
A.2 个 B.4 个 C.6 个 D.8 个
3.(3 分)如图,BE CF , AE BC ,DF BC ,要根据“ HL ”证明Rt ABE Rt DCF ,则还需
要添加一个条件是 ( )
A. AE DF B. A D C. B C D. AB DC
4.(3 分)如图,在 ABC 中, ACB 90 ,过点C 作CD AB 于D , A 30 ,BD 1,则 AB
的值是 ( )
A.1 B.2 C.3 D.4
5.(3 分)如图,在 ABC 中, ACB 90 , ABC 60 , BD平分 ABC , P 点是 BD的中点,
若 BD 6 ,则CP 的长为 ( )
A.3 B.3.5 C.4 D.4.5
6.(3 分)点 D 在 ABC 的边 BC 上, ABD 和 ACD的面积相等,则 AD 是 ( )
A.中线 B.高线 C.角平分线 D.中垂线
7.(3 分)如图, ABC 中, AB AC 13 , BC 10, AD 平分 BAC 交 BC 于点 D , AD 的垂直
平分线交 AC 于点 E ,连接 DE ,则 CDE 的周长为 ( )
A.23 B.26 C.18 D.15
8.(3 分)如图,在四边形 ABDC 中, B D 90 , BAC 与 ACD 的平分线交于点O ,且点O
在线段 BD上, BD 4,则点O 到边 AC 的距离是 ( )
A.1 B.1.5 C.2 D.3
9.(3 分)如图,等腰 ABC 的面积为 S ,AB AC m ,点 D 为 BC 边上任意一点,DE AB于 E ,
DF AC 于 F ,则DE DF ( )
S 2S S 2m
A. B. C. D.
m m 2m S
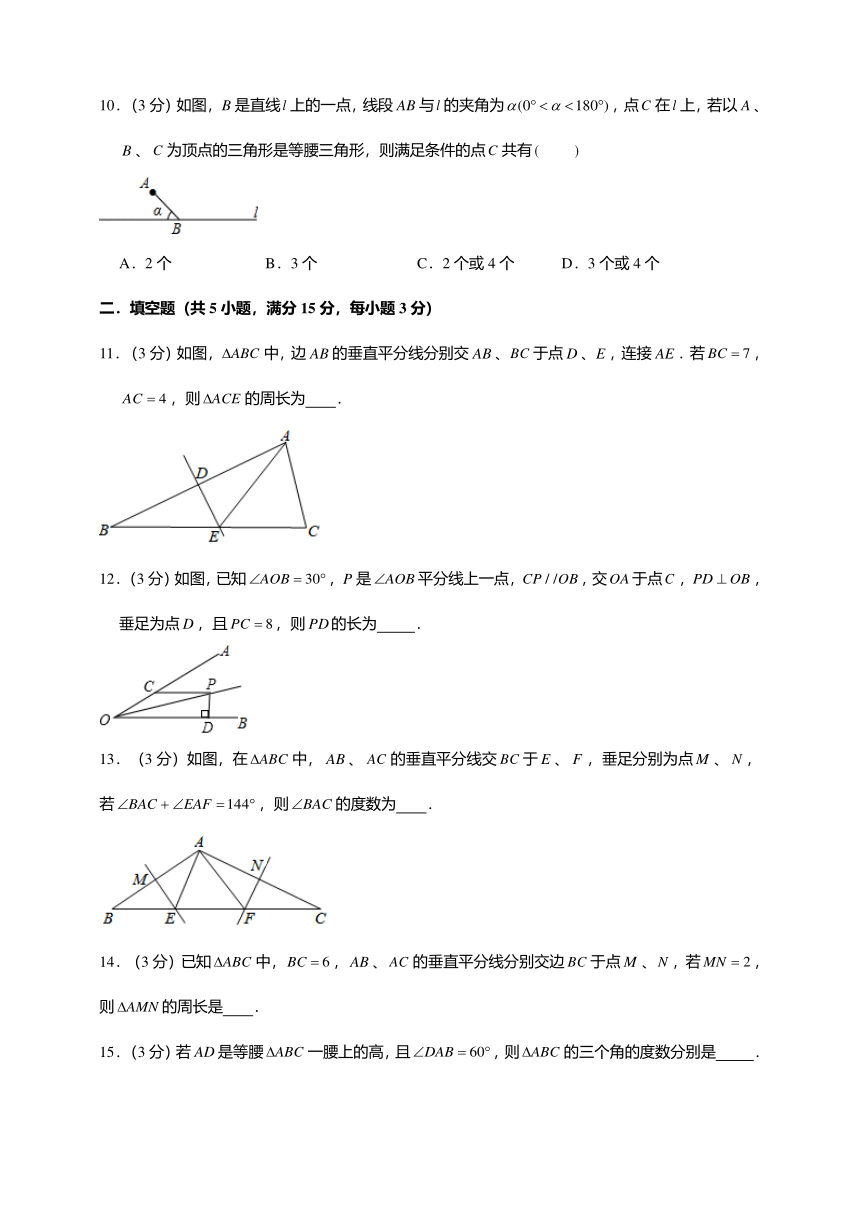
10.(3 分)如图,B 是直线 l 上的一点,线段 AB 与 l 的夹角为 (0 180 ) ,点C 在 l 上,若以 A 、
B 、C 为顶点的三角形是等腰三角形,则满足条件的点C 共有 ( )
A.2 个 B.3 个 C.2 个或 4 个 D.3 个或 4 个
二.填空题(共 5 小题,满分 15 分,每小题 3 分)
11.(3 分)如图, ABC 中,边 AB 的垂直平分线分别交 AB 、BC 于点 D 、E ,连接 AE .若 BC 7 ,
AC 4 ,则 ACE 的周长为 .
12.(3 分)如图,已知 AOB 30 ,P 是 AOB 平分线上一点,CP / /OB,交OA于点C ,PD OB ,
垂足为点 D ,且 PC 8,则 PD的长为 .
13.(3 分)如图,在 ABC 中, AB 、 AC 的垂直平分线交 BC 于 E 、 F ,垂足分别为点M 、 N ,
若 BAC EAF 144 ,则 BAC 的度数为 .
14.(3 分)已知 ABC 中,BC 6 ,AB 、AC 的垂直平分线分别交边 BC 于点M 、N ,若MN 2 ,
则 AMN 的周长是 .
15.(3 分)若 AD 是等腰 ABC 一腰上的高,且 DAB 60 ,则 ABC 的三个角的度数分别是 .
三.解答题(共 7 小题,满分 55 分)
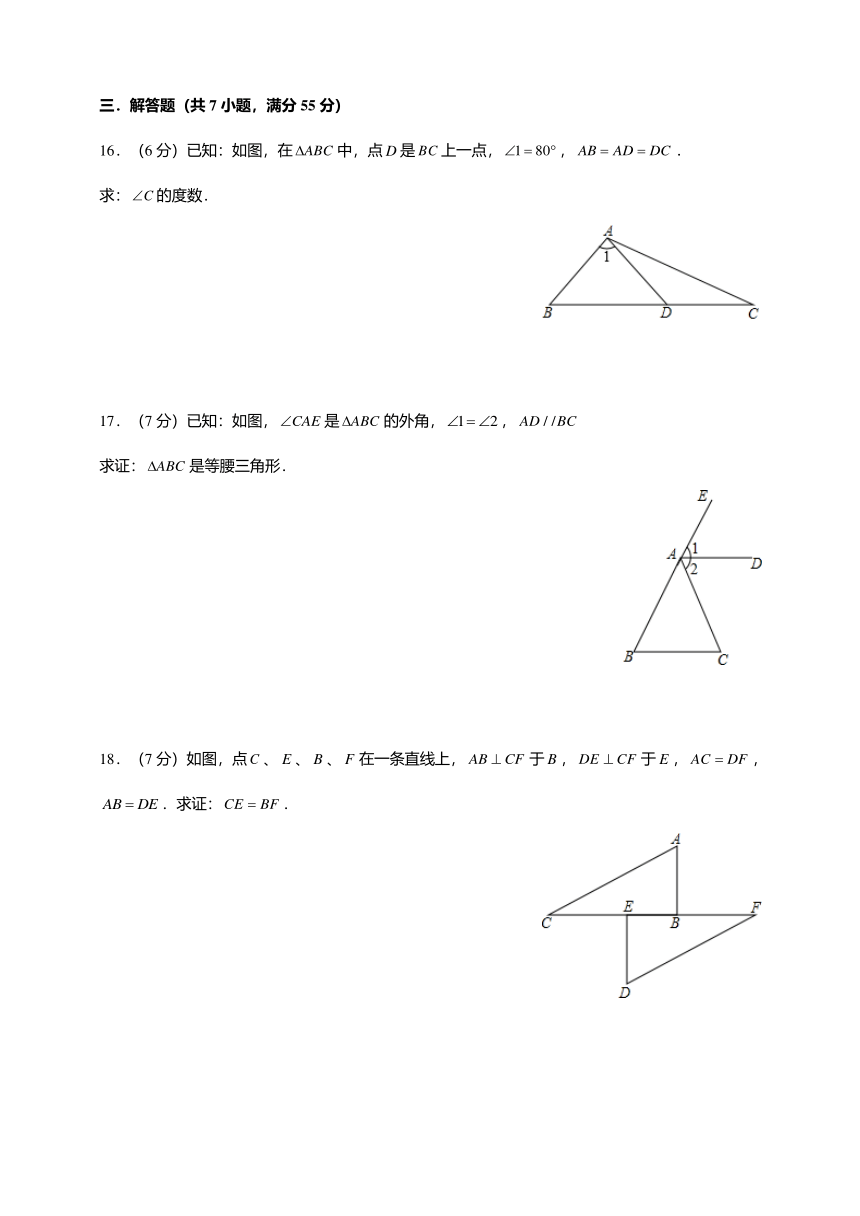
16.(6 分)已知:如图,在 ABC 中,点 D 是 BC 上一点, 1 80 , AB AD DC .
求: C 的度数.
17.(7 分)已知:如图, CAE 是 ABC 的外角, 1 2, AD / /BC
求证: ABC 是等腰三角形.
18.(7 分)如图,点C 、 E 、 B 、 F 在一条直线上, AB CF 于 B , DE CF 于 E , AC DF ,
AB DE .求证:CE BF .
19.(8 分)如图,已知 BD为 ABC 的平分线,AB BC ,点 P 在 BD上,PM AD 于M ,PN CD
于 N ,求证: PM PN .
20.(8 分)如图,在 ABC 中,BD是 ABC 的平分线,过点C 作CE BD ,交 BD的延长线于点 E ,
ABC 60 , ECD 15 .
(1)直接写出 ADB的度数是 ;
(2)求证: BD AB;
(3)若 AB 2 ,求 BC 的长.
21.(9 分)如图, 已知在 ABC中, AB AC , BAC 120 , AC 的垂直平分线EF 交 AC
于点E ,交BC 于点F . 试探索BF 与CF 的数量关系, 写出你的结论并证明 .
22.(10 分)如图,已知 AC BC , AD BD, E 为 AB 的中点,
(1)如图 1,求证: ECD是等腰三角形;
(2)如图 2,CD 与 AB 交点为 F ,若 AD BD , EF 3, DE 4 ,求CD 的长.
北师大八年级下册第 1 单元测试卷
参考答案与试题解析
一.选择题(共 10 小题,满分 30 分,每小题 3 分)
1.(3 分)等腰三角形的两边长分别为 5 和 11,则这个三角形的周长为 ( )
A.16 B.27 C.16 或 27 D.21 或 27
【解答】解:①11 是腰长时,
三角形的三边分别为 11、11、5,能组成三角形,
周长 11 11 5 27 ;
②11 是底边时,
三角形的三边分别为 11、5、5,
5 5 10 11,
不能组成三角形,
综上所述,三角形的周长为 27.
故选: B .
2.(3 分)如图,矩形 ABCD 中, AB BC ,对角线 AC 、BD相交于点O ,则图中的等腰三角形有
( )
A.2 个 B.4 个 C.6 个 D.8 个
【解答】解: 矩形 ABCD 中, AB BC ,对角线 AC 、 BD相交于点O ,
OA OB OC OD ,
图中的等腰三角形有 AOB 、 AOD 、 COD 、 BOC 四个.
故选: B .
3.(3 分)如图,BE CF , AE BC ,DF BC ,要根据“ HL ”证明Rt ABE Rt DCF ,则还需
要添加一个条件是 ( )
A. AE DF B. A D C. B C D. AB DC
【解答】解:条件是 AB CD ,
理由是: AE BC , DF BC ,
CFD AEB 90 ,
在Rt ABE 和Rt DCF中,
AB CD
,
BE CF
Rt ABE Rt DCF(HL),
故选: D .
4.(3 分)如图,在 ABC 中, ACB 90 ,过点C 作CD AB 于D , A 30 ,BD 1,则 AB
的值是 ( )
A.1 B.2 C.3 D.4
【解答】解: ABC 中, ACB 90 , A 30 ,
B 60 ,又CD AB ,
BCD 30 ,
在Rt BCD 中, BCD 30 , BD 1,
可得 BC 2BD 2 ,
在Rt ABC中, A 30 , BC 2 ,
则 AB 2BC 4.
故选: D .
5.(3 分)如图,在 ABC 中, ACB 90 , ABC 60 , BD平分 ABC , P 点是 BD的中点,
若 BD 6 ,则CP 的长为 ( )
A.3 B.3.5 C.4 D.4.5
【解答】解: ACB 90 , ABC 60 ,
A 30 ,
BD 平分 ABC ,
CBD DBA 30 ,
BD AD 6 ,
P点是 BD的中点,
1
CP BD 3,
2
故选: A .
6.(3 分)点 D 在 ABC 的边 BC 上, ABD 和 ACD的面积相等,则 AD 是 ( )
A.中线 B.高线 C.角平分线 D.中垂线
【解答】解: 点 D 在 ABC 的边 BC 上, ABD 和 ACD的面积相等,
AD是 ABC 的中线,
故选: A .
7.(3 分)如图, ABC 中, AB AC 13 , BC 10, AD 平分 BAC 交 BC 于点 D , AD 的垂直
平分线交 AC 于点 E ,连接 DE ,则 CDE 的周长为 ( )
A.23 B.26 C.18 D.15
【解答】解: ABC 中, AB AC 13 , BC 10, AD 平分 BAC 交 BC 于点 D ,
1
CD BC 5.
2
AD的垂直平分线交 AC 于点 E ,
AE DE ,
CDE 的周长 (CE DE) CD (AE CE) CD AC CD 13 5 18.
故选:C .
8.(3 分)如图,在四边形 ABDC 中, B D 90 , BAC 与 ACD 的平分线交于点O ,且点O
在线段 BD上, BD 4,则点O 到边 AC 的距离是 ( )
A.1 B.1.5 C.2 D.3
【解答】解:过O 作OE AC 于 E ,
B D 90 , BAC 与 ACD 的平分线交于点O ,
OB OE OD ,
BD 4 ,
OB OE OD 2 ,
点O 到边 AC 的距离是 2,
故选:C .
9.(3 分)如图,等腰 ABC 的面积为 S ,AB AC m ,点 D 为 BC 边上任意一点,DE AB于 E ,
DF AC 于 F ,则DE DF ( )
S 2S S 2m
A. B. C. D.
m m 2m S
【解答】解:如图所示:连接 AD ,
AB AC m , ABC 的面积是 S ,
1 1
AB DE AC DF S ,
2 2
AB AC m ,
2S
DE DF ,
m
故选: B .
10.(3 分)如图,B 是直线 l 上的一点,线段 AB 与 l 的夹角为 (0 180 ) ,点C 在 l 上,若以 A 、
B 、C 为顶点的三角形是等腰三角形,则满足条件的点C 共有 ( )
A.2 个 B.3 个 C.2 个或 4 个 D.3 个或 4 个
【解答】解;如图 1,当 90 ,
只有两个点符合要求,
如图 2,当 为锐角与钝角时,
符合条件的点有 4 个,
分别是 AC AB , AB BC , AC BC , AB BC . 3 2 1
满足条件的点C 共有:2 或 4 个.
故选:C .
二.填空题(共 5 小题,满分 15 分,每小题 3 分)
11.(3 分)如图, ABC 中,边 AB 的垂直平分线分别交 AB 、BC 于点 D 、E ,连接 AE .若 BC 7 ,
AC 4 ,则 ACE 的周长为 11 .
【解答】解: DE 是 AB 的垂直平分线,
EB EA,
ACE 的周长 AE EC AC BE EC AC BC AC 11,
故答案为:11.
12.(3 分)如图,已知 AOB 30 ,P 是 AOB 平分线上一点,CP / /OB,交OA于点C ,PD OB ,
垂足为点 D ,且 PC 8,则 PD的长为 4 .
【解答】解:作 PE OA 于 E ,
P是 AOB 平分线上一点,
AOP BOP 15 ,
PC / /OB ,
POD OPC ,
PCE POC OPC POC POD AOB 30 ,
1
PE PC 4 ,
2
P是 AOB 平分线上一点, PD OB , PE OA ,
PD PE 4,
故答案为:4.
13.(3 分)如图,在 ABC 中, AB 、 AC 的垂直平分线交 BC 于 E 、 F ,垂足分别为点M 、 N ,
若 BAC EAF 144 ,则 BAC 的度数为 108 .
【解答】解: AE BE , AF CF ,
B BAE , C CAF .
设 BAC x ,
B C 180 x ,
BAE CAF B C 180 x ,
EAF BAC ( BAE CAF) x (180 x) 2x 180 .
BAC EAF 144 ,
x (2x 180 ) 144 ,
解得 x 108 ,
即 BAC 108 .
故答案为:108
14.(3 分)已知 ABC 中,BC 6 ,AB 、AC 的垂直平分线分别交边 BC 于点M 、N ,若MN 2 ,
则 AMN 的周长是 6 或 10 .
【解答】解:图 1, 直线MP为线段 AB 的垂直平分线,
MA MB,
又直线 NQ 为线段 AC 的垂直平分线,
NA NC ,
AMN 的周长 l AM MN AN BM MN NC BC ,
又 BC 6 ,
则 AMN 的周长为 6,
如图 2, AMN 的周长 l AM MN AN BM MN NC BC 2MN ,
又 BC 6 ,
则 AMN 的周长为 10,
故答案为:6 或 10
15.(3 分)若 AD 是等腰 ABC 一腰上的高,且 DAB 60 ,则 ABC 的三个角的度数分别是
BAC 15 , B 150 , C 15 或 BAC 75 , B 30 , C 75 或 BAC 30 , B 30 ,
C 120 .
【解答】解:①如图, DAB 60 , ADB 90 ,
B 30 ,
AB BC ,
BAC C 75 .
②如图, DAB 60 , ADB 90 ,
DBA 30 ,
AB BC ,
BAC C 15 , B 150 .
③如图, DAB 60 , ADB 90 ,
B 30 ,
AC BC ,
BAC B 30 , C 120 .
故答案为: BAC 15 , B 150 , C 15 或 BAC 75 , B 30 , C 75 或 BAC 30 ,
B 30 , C 120 .
三.解答题(共 7 小题,满分 55 分)
16.(6 分)已知:如图,在 ABC 中,点 D 是 BC 上一点, 1 80 , AB AD DC .
求: C 的度数.
【解答】解: 1 80 , AB AD,
1
B ADB (180 1) 50 ,
2
AD CD ,
C DAC ,
C DAC ADB 50 ,
1
C DAC 50 25 .
2
17.(7 分)已知:如图, CAE 是 ABC 的外角, 1 2, AD / /BC
求证: ABC 是等腰三角形.
【解答】证明: AD / /BC ,(已知)
1 B,(两直线平行,同位角相等)
2 C ,(两直线平行,内错角相等)
1 2,(已知)
B C ,
AB AC .(等角对等边)
即 ABC 是等腰三角形.
18.(7 分)如图,点C 、 E 、 B 、 F 在一条直线上, AB CF 于 B , DE CF 于 E , AC DF ,
AB DE .求证:CE BF .
【解答】证明: AB CF ,DE CF ,
ABC DEF 90 .
在Rt ABC和Rt DEF 中,
AC DF
,
AB DE
Rt ABC Rt DEF(HL).
BC EF .
BC BE EF BE .
即:CE BF .
19.(8 分)如图,已知 BD为 ABC 的平分线,AB BC ,点 P 在 BD上,PM AD 于M ,PN CD
于 N ,求证: PM PN .
【解答】证明: BD 为 ABC 的平分线,
ABD CBD ,
在 ABD 和 CBD中,
AB BC
ABD CBD ,
BD BD
ABD CBD(SAS) ,
ADB CDB ,
点 P 在 BD上, PM AD , PN CD ,
PM PN .
20.(8 分)如图,在 ABC 中,BD是 ABC 的平分线,过点C 作CE BD ,交 BD的延长线于点 E ,
ABC 60 , ECD 15 .
(1)直接写出 ADB的度数是 75 ;
(2)求证: BD AB;
(3)若 AB 2 ,求 BC 的长.
【解答】解:(1) CE BE ,
E 90 ,
ECD 15 ,
ADB CDE 90 15 75
故答案为 75 .
(2)证明: BD 平分 ABC ,
ABC 60 ,
ABD DBC 30 ,
ADB 75 ,
A 75 ,
A ADB,
AB DB.
(3)过点 D 作 DF BC ,交 BC 于 F 点.
DF BC ,
DFB DFC 90 ,
DBF 30 ,
1
DF BD,
2
BD AB 2,
DF 1,
FB 3 ,
CE BE ,
E 90 ,
DBC 30 ,
ECB 60 ,
ECD 15 ,
DCB 45 ,
DCF FDC 45 ,
FD FC 1,
BC 3 1.
21.(9 分)如图, 已知在 ABC中, AB AC , BAC 120 , AC 的垂直平分线EF 交 AC
于点E ,交BC 于点F . 试探索BF 与CF 的数量关系, 写出你的结论并证明 .
【解答】解:BF 2CF .
证明: 连接 AF ,
AB AC, BAC 120
B C 30 ,
EF 垂直平分 AC ,
AF CF ,
CAF C 30 ,
AFB CAF C 60 ,
BAF 180 B AFB 90 ,
BF 2AF ,
BF 2CF .
22.(10 分)如图,已知 AC BC , AD BD, E 为 AB 的中点,
(1)如图 1,求证: ECD是等腰三角形;
(2)如图 2,CD 与 AB 交点为 F ,若 AD BD , EF 3, DE 4 ,求CD 的长.
【解答】(1)证明: AC BC , AD BD,
ACB 90 , ADB 90 ,又 E 为 AB 的中点,
1 1
CE AB , DE AB
2 2
CE DE ,即 ECD是等腰三角形;
(2) AD BD, E 为 AB 的中点,
DE AB ,
已知 DE 4 , EF 3,
DF 5,
过点 E 作 EH CD ,
FED 90 , EH DF ,
EF ED 12
EH ,
DF 5
16
DH DE2 EH 2 ,
5
ECD 是等腰三角形,
32
CD 2DH .
5
一.选择题(共 10 小题,满分 30 分,每小题 3 分)
1.(3 分)等腰三角形的两边长分别为 5 和 11,则这个三角形的周长为 ( )
A.16 B.27 C.16 或 27 D.21 或 27
2.(3 分)如图,矩形 ABCD 中, AB BC ,对角线 AC 、BD相交于点O ,则图中的等腰三角形有
( )
A.2 个 B.4 个 C.6 个 D.8 个
3.(3 分)如图,BE CF , AE BC ,DF BC ,要根据“ HL ”证明Rt ABE Rt DCF ,则还需
要添加一个条件是 ( )
A. AE DF B. A D C. B C D. AB DC
4.(3 分)如图,在 ABC 中, ACB 90 ,过点C 作CD AB 于D , A 30 ,BD 1,则 AB
的值是 ( )
A.1 B.2 C.3 D.4
5.(3 分)如图,在 ABC 中, ACB 90 , ABC 60 , BD平分 ABC , P 点是 BD的中点,
若 BD 6 ,则CP 的长为 ( )
A.3 B.3.5 C.4 D.4.5
6.(3 分)点 D 在 ABC 的边 BC 上, ABD 和 ACD的面积相等,则 AD 是 ( )
A.中线 B.高线 C.角平分线 D.中垂线
7.(3 分)如图, ABC 中, AB AC 13 , BC 10, AD 平分 BAC 交 BC 于点 D , AD 的垂直
平分线交 AC 于点 E ,连接 DE ,则 CDE 的周长为 ( )
A.23 B.26 C.18 D.15
8.(3 分)如图,在四边形 ABDC 中, B D 90 , BAC 与 ACD 的平分线交于点O ,且点O
在线段 BD上, BD 4,则点O 到边 AC 的距离是 ( )
A.1 B.1.5 C.2 D.3
9.(3 分)如图,等腰 ABC 的面积为 S ,AB AC m ,点 D 为 BC 边上任意一点,DE AB于 E ,
DF AC 于 F ,则DE DF ( )
S 2S S 2m
A. B. C. D.
m m 2m S
10.(3 分)如图,B 是直线 l 上的一点,线段 AB 与 l 的夹角为 (0 180 ) ,点C 在 l 上,若以 A 、
B 、C 为顶点的三角形是等腰三角形,则满足条件的点C 共有 ( )
A.2 个 B.3 个 C.2 个或 4 个 D.3 个或 4 个
二.填空题(共 5 小题,满分 15 分,每小题 3 分)
11.(3 分)如图, ABC 中,边 AB 的垂直平分线分别交 AB 、BC 于点 D 、E ,连接 AE .若 BC 7 ,
AC 4 ,则 ACE 的周长为 .
12.(3 分)如图,已知 AOB 30 ,P 是 AOB 平分线上一点,CP / /OB,交OA于点C ,PD OB ,
垂足为点 D ,且 PC 8,则 PD的长为 .
13.(3 分)如图,在 ABC 中, AB 、 AC 的垂直平分线交 BC 于 E 、 F ,垂足分别为点M 、 N ,
若 BAC EAF 144 ,则 BAC 的度数为 .
14.(3 分)已知 ABC 中,BC 6 ,AB 、AC 的垂直平分线分别交边 BC 于点M 、N ,若MN 2 ,
则 AMN 的周长是 .
15.(3 分)若 AD 是等腰 ABC 一腰上的高,且 DAB 60 ,则 ABC 的三个角的度数分别是 .
三.解答题(共 7 小题,满分 55 分)
16.(6 分)已知:如图,在 ABC 中,点 D 是 BC 上一点, 1 80 , AB AD DC .
求: C 的度数.
17.(7 分)已知:如图, CAE 是 ABC 的外角, 1 2, AD / /BC
求证: ABC 是等腰三角形.
18.(7 分)如图,点C 、 E 、 B 、 F 在一条直线上, AB CF 于 B , DE CF 于 E , AC DF ,
AB DE .求证:CE BF .
19.(8 分)如图,已知 BD为 ABC 的平分线,AB BC ,点 P 在 BD上,PM AD 于M ,PN CD
于 N ,求证: PM PN .
20.(8 分)如图,在 ABC 中,BD是 ABC 的平分线,过点C 作CE BD ,交 BD的延长线于点 E ,
ABC 60 , ECD 15 .
(1)直接写出 ADB的度数是 ;
(2)求证: BD AB;
(3)若 AB 2 ,求 BC 的长.
21.(9 分)如图, 已知在 ABC中, AB AC , BAC 120 , AC 的垂直平分线EF 交 AC
于点E ,交BC 于点F . 试探索BF 与CF 的数量关系, 写出你的结论并证明 .
22.(10 分)如图,已知 AC BC , AD BD, E 为 AB 的中点,
(1)如图 1,求证: ECD是等腰三角形;
(2)如图 2,CD 与 AB 交点为 F ,若 AD BD , EF 3, DE 4 ,求CD 的长.
北师大八年级下册第 1 单元测试卷
参考答案与试题解析
一.选择题(共 10 小题,满分 30 分,每小题 3 分)
1.(3 分)等腰三角形的两边长分别为 5 和 11,则这个三角形的周长为 ( )
A.16 B.27 C.16 或 27 D.21 或 27
【解答】解:①11 是腰长时,
三角形的三边分别为 11、11、5,能组成三角形,
周长 11 11 5 27 ;
②11 是底边时,
三角形的三边分别为 11、5、5,
5 5 10 11,
不能组成三角形,
综上所述,三角形的周长为 27.
故选: B .
2.(3 分)如图,矩形 ABCD 中, AB BC ,对角线 AC 、BD相交于点O ,则图中的等腰三角形有
( )
A.2 个 B.4 个 C.6 个 D.8 个
【解答】解: 矩形 ABCD 中, AB BC ,对角线 AC 、 BD相交于点O ,
OA OB OC OD ,
图中的等腰三角形有 AOB 、 AOD 、 COD 、 BOC 四个.
故选: B .
3.(3 分)如图,BE CF , AE BC ,DF BC ,要根据“ HL ”证明Rt ABE Rt DCF ,则还需
要添加一个条件是 ( )
A. AE DF B. A D C. B C D. AB DC
【解答】解:条件是 AB CD ,
理由是: AE BC , DF BC ,
CFD AEB 90 ,
在Rt ABE 和Rt DCF中,
AB CD
,
BE CF
Rt ABE Rt DCF(HL),
故选: D .
4.(3 分)如图,在 ABC 中, ACB 90 ,过点C 作CD AB 于D , A 30 ,BD 1,则 AB
的值是 ( )
A.1 B.2 C.3 D.4
【解答】解: ABC 中, ACB 90 , A 30 ,
B 60 ,又CD AB ,
BCD 30 ,
在Rt BCD 中, BCD 30 , BD 1,
可得 BC 2BD 2 ,
在Rt ABC中, A 30 , BC 2 ,
则 AB 2BC 4.
故选: D .
5.(3 分)如图,在 ABC 中, ACB 90 , ABC 60 , BD平分 ABC , P 点是 BD的中点,
若 BD 6 ,则CP 的长为 ( )
A.3 B.3.5 C.4 D.4.5
【解答】解: ACB 90 , ABC 60 ,
A 30 ,
BD 平分 ABC ,
CBD DBA 30 ,
BD AD 6 ,
P点是 BD的中点,
1
CP BD 3,
2
故选: A .
6.(3 分)点 D 在 ABC 的边 BC 上, ABD 和 ACD的面积相等,则 AD 是 ( )
A.中线 B.高线 C.角平分线 D.中垂线
【解答】解: 点 D 在 ABC 的边 BC 上, ABD 和 ACD的面积相等,
AD是 ABC 的中线,
故选: A .
7.(3 分)如图, ABC 中, AB AC 13 , BC 10, AD 平分 BAC 交 BC 于点 D , AD 的垂直
平分线交 AC 于点 E ,连接 DE ,则 CDE 的周长为 ( )
A.23 B.26 C.18 D.15
【解答】解: ABC 中, AB AC 13 , BC 10, AD 平分 BAC 交 BC 于点 D ,
1
CD BC 5.
2
AD的垂直平分线交 AC 于点 E ,
AE DE ,
CDE 的周长 (CE DE) CD (AE CE) CD AC CD 13 5 18.
故选:C .
8.(3 分)如图,在四边形 ABDC 中, B D 90 , BAC 与 ACD 的平分线交于点O ,且点O
在线段 BD上, BD 4,则点O 到边 AC 的距离是 ( )
A.1 B.1.5 C.2 D.3
【解答】解:过O 作OE AC 于 E ,
B D 90 , BAC 与 ACD 的平分线交于点O ,
OB OE OD ,
BD 4 ,
OB OE OD 2 ,
点O 到边 AC 的距离是 2,
故选:C .
9.(3 分)如图,等腰 ABC 的面积为 S ,AB AC m ,点 D 为 BC 边上任意一点,DE AB于 E ,
DF AC 于 F ,则DE DF ( )
S 2S S 2m
A. B. C. D.
m m 2m S
【解答】解:如图所示:连接 AD ,
AB AC m , ABC 的面积是 S ,
1 1
AB DE AC DF S ,
2 2
AB AC m ,
2S
DE DF ,
m
故选: B .
10.(3 分)如图,B 是直线 l 上的一点,线段 AB 与 l 的夹角为 (0 180 ) ,点C 在 l 上,若以 A 、
B 、C 为顶点的三角形是等腰三角形,则满足条件的点C 共有 ( )
A.2 个 B.3 个 C.2 个或 4 个 D.3 个或 4 个
【解答】解;如图 1,当 90 ,
只有两个点符合要求,
如图 2,当 为锐角与钝角时,
符合条件的点有 4 个,
分别是 AC AB , AB BC , AC BC , AB BC . 3 2 1
满足条件的点C 共有:2 或 4 个.
故选:C .
二.填空题(共 5 小题,满分 15 分,每小题 3 分)
11.(3 分)如图, ABC 中,边 AB 的垂直平分线分别交 AB 、BC 于点 D 、E ,连接 AE .若 BC 7 ,
AC 4 ,则 ACE 的周长为 11 .
【解答】解: DE 是 AB 的垂直平分线,
EB EA,
ACE 的周长 AE EC AC BE EC AC BC AC 11,
故答案为:11.
12.(3 分)如图,已知 AOB 30 ,P 是 AOB 平分线上一点,CP / /OB,交OA于点C ,PD OB ,
垂足为点 D ,且 PC 8,则 PD的长为 4 .
【解答】解:作 PE OA 于 E ,
P是 AOB 平分线上一点,
AOP BOP 15 ,
PC / /OB ,
POD OPC ,
PCE POC OPC POC POD AOB 30 ,
1
PE PC 4 ,
2
P是 AOB 平分线上一点, PD OB , PE OA ,
PD PE 4,
故答案为:4.
13.(3 分)如图,在 ABC 中, AB 、 AC 的垂直平分线交 BC 于 E 、 F ,垂足分别为点M 、 N ,
若 BAC EAF 144 ,则 BAC 的度数为 108 .
【解答】解: AE BE , AF CF ,
B BAE , C CAF .
设 BAC x ,
B C 180 x ,
BAE CAF B C 180 x ,
EAF BAC ( BAE CAF) x (180 x) 2x 180 .
BAC EAF 144 ,
x (2x 180 ) 144 ,
解得 x 108 ,
即 BAC 108 .
故答案为:108
14.(3 分)已知 ABC 中,BC 6 ,AB 、AC 的垂直平分线分别交边 BC 于点M 、N ,若MN 2 ,
则 AMN 的周长是 6 或 10 .
【解答】解:图 1, 直线MP为线段 AB 的垂直平分线,
MA MB,
又直线 NQ 为线段 AC 的垂直平分线,
NA NC ,
AMN 的周长 l AM MN AN BM MN NC BC ,
又 BC 6 ,
则 AMN 的周长为 6,
如图 2, AMN 的周长 l AM MN AN BM MN NC BC 2MN ,
又 BC 6 ,
则 AMN 的周长为 10,
故答案为:6 或 10
15.(3 分)若 AD 是等腰 ABC 一腰上的高,且 DAB 60 ,则 ABC 的三个角的度数分别是
BAC 15 , B 150 , C 15 或 BAC 75 , B 30 , C 75 或 BAC 30 , B 30 ,
C 120 .
【解答】解:①如图, DAB 60 , ADB 90 ,
B 30 ,
AB BC ,
BAC C 75 .
②如图, DAB 60 , ADB 90 ,
DBA 30 ,
AB BC ,
BAC C 15 , B 150 .
③如图, DAB 60 , ADB 90 ,
B 30 ,
AC BC ,
BAC B 30 , C 120 .
故答案为: BAC 15 , B 150 , C 15 或 BAC 75 , B 30 , C 75 或 BAC 30 ,
B 30 , C 120 .
三.解答题(共 7 小题,满分 55 分)
16.(6 分)已知:如图,在 ABC 中,点 D 是 BC 上一点, 1 80 , AB AD DC .
求: C 的度数.
【解答】解: 1 80 , AB AD,
1
B ADB (180 1) 50 ,
2
AD CD ,
C DAC ,
C DAC ADB 50 ,
1
C DAC 50 25 .
2
17.(7 分)已知:如图, CAE 是 ABC 的外角, 1 2, AD / /BC
求证: ABC 是等腰三角形.
【解答】证明: AD / /BC ,(已知)
1 B,(两直线平行,同位角相等)
2 C ,(两直线平行,内错角相等)
1 2,(已知)
B C ,
AB AC .(等角对等边)
即 ABC 是等腰三角形.
18.(7 分)如图,点C 、 E 、 B 、 F 在一条直线上, AB CF 于 B , DE CF 于 E , AC DF ,
AB DE .求证:CE BF .
【解答】证明: AB CF ,DE CF ,
ABC DEF 90 .
在Rt ABC和Rt DEF 中,
AC DF
,
AB DE
Rt ABC Rt DEF(HL).
BC EF .
BC BE EF BE .
即:CE BF .
19.(8 分)如图,已知 BD为 ABC 的平分线,AB BC ,点 P 在 BD上,PM AD 于M ,PN CD
于 N ,求证: PM PN .
【解答】证明: BD 为 ABC 的平分线,
ABD CBD ,
在 ABD 和 CBD中,
AB BC
ABD CBD ,
BD BD
ABD CBD(SAS) ,
ADB CDB ,
点 P 在 BD上, PM AD , PN CD ,
PM PN .
20.(8 分)如图,在 ABC 中,BD是 ABC 的平分线,过点C 作CE BD ,交 BD的延长线于点 E ,
ABC 60 , ECD 15 .
(1)直接写出 ADB的度数是 75 ;
(2)求证: BD AB;
(3)若 AB 2 ,求 BC 的长.
【解答】解:(1) CE BE ,
E 90 ,
ECD 15 ,
ADB CDE 90 15 75
故答案为 75 .
(2)证明: BD 平分 ABC ,
ABC 60 ,
ABD DBC 30 ,
ADB 75 ,
A 75 ,
A ADB,
AB DB.
(3)过点 D 作 DF BC ,交 BC 于 F 点.
DF BC ,
DFB DFC 90 ,
DBF 30 ,
1
DF BD,
2
BD AB 2,
DF 1,
FB 3 ,
CE BE ,
E 90 ,
DBC 30 ,
ECB 60 ,
ECD 15 ,
DCB 45 ,
DCF FDC 45 ,
FD FC 1,
BC 3 1.
21.(9 分)如图, 已知在 ABC中, AB AC , BAC 120 , AC 的垂直平分线EF 交 AC
于点E ,交BC 于点F . 试探索BF 与CF 的数量关系, 写出你的结论并证明 .
【解答】解:BF 2CF .
证明: 连接 AF ,
AB AC, BAC 120
B C 30 ,
EF 垂直平分 AC ,
AF CF ,
CAF C 30 ,
AFB CAF C 60 ,
BAF 180 B AFB 90 ,
BF 2AF ,
BF 2CF .
22.(10 分)如图,已知 AC BC , AD BD, E 为 AB 的中点,
(1)如图 1,求证: ECD是等腰三角形;
(2)如图 2,CD 与 AB 交点为 F ,若 AD BD , EF 3, DE 4 ,求CD 的长.
【解答】(1)证明: AC BC , AD BD,
ACB 90 , ADB 90 ,又 E 为 AB 的中点,
1 1
CE AB , DE AB
2 2
CE DE ,即 ECD是等腰三角形;
(2) AD BD, E 为 AB 的中点,
DE AB ,
已知 DE 4 , EF 3,
DF 5,
过点 E 作 EH CD ,
FED 90 , EH DF ,
EF ED 12
EH ,
DF 5
16
DH DE2 EH 2 ,
5
ECD 是等腰三角形,
32
CD 2DH .
5
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
