八年级数学(下)学案案(第八章)8.3 怎样判断三角形全等(1)
文档属性
| 名称 | 八年级数学(下)学案案(第八章)8.3 怎样判断三角形全等(1) |  | |
| 格式 | zip | ||
| 文件大小 | 72.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-22 15:05:16 | ||
图片预览

文档简介
八年级数学(下)学案案(第八章)
8.3 怎样判断三角形全等(1)
【学习目标】1.熟记角边角公理、角角边推论的内容;
2.知道能角边角公理及其推论证明两个三角形全等。
【课前预习】
学习任务一:
(1)如图1所示,图中两个三角形能够完全重合,下面写法中正确的是( )
A.△ABE≌△AFB B.△ABE≌△ABF C.△ABE≌△FBA D.△ABE≌△FAB
图1 图2
(2)如图2所示,△ABC≌△CDA,并且AB=CD,下列结论中错误的是( )
A.∠1=∠2 B.AC=CA C.∠D=∠B D.AC=BC
学习任务二:
通过P28实验与探究你得到的结论是
判定1:(角边角判定):
应用格式:
练习:如图,已知∠C=∠E,AC=AE
试说明 △ABC≌△ADE
学习任务三:
改变公理1的条件:有两角和其中一角的对边对应相等,
这样的两个三角形是否全等呢?
如图,已知∠FAB=∠EAB,∠F=∠E △ABF与△ABE
全等吗?为什么?
推论: (角角边判定)
(注意区别“对应边和对边”)
【课中探究】
问题一:阅读教材第28—29页内容,思考并总结本节课学习的主要内容是什么?
问题二:
1.如图:已知M是△ABC的边BC上一点,
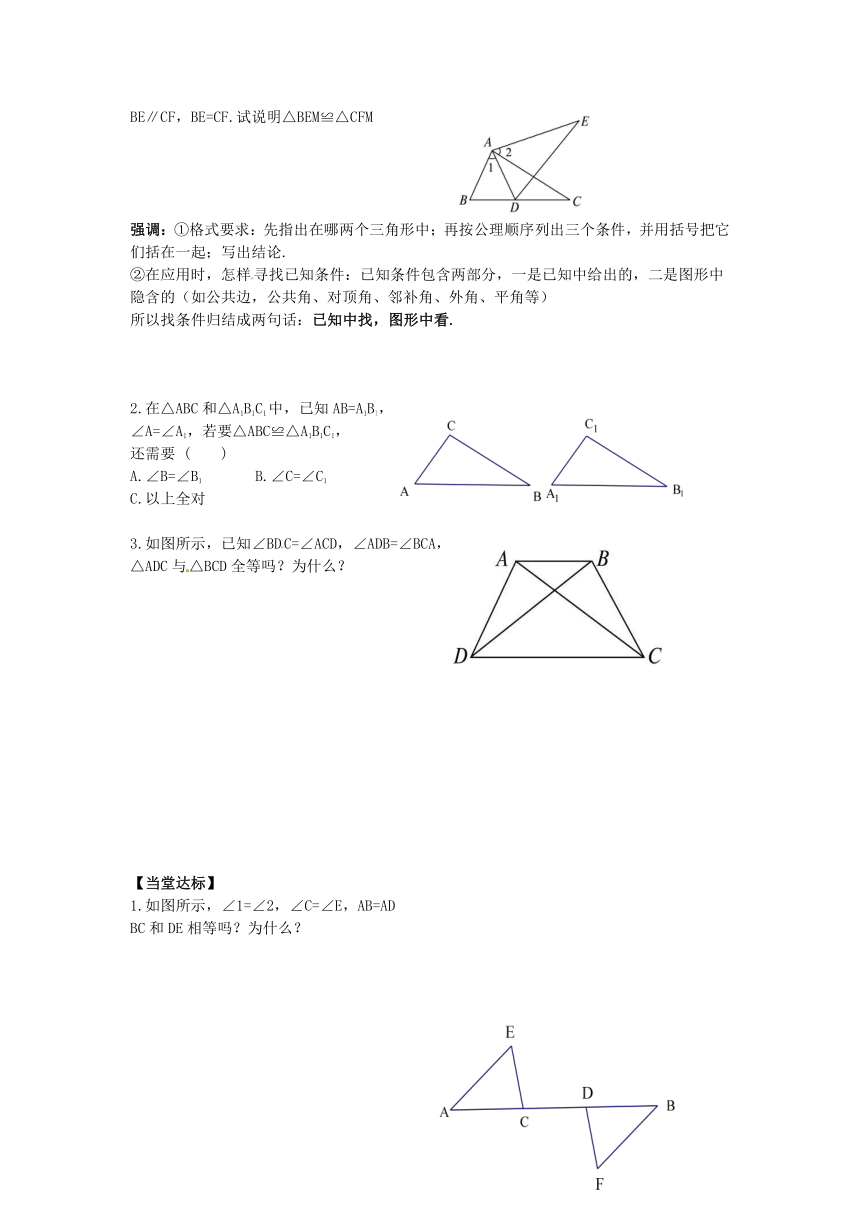
BE∥CF,BE=CF.试说明△BEM≌△CFM
强调:①格式要求:先指出在哪两个三角形中;再按公理顺序列出三个条件,并用括号把它们括在一起;写出结论.
②在应用时,怎样寻找已知条件:已知条件包含两部分,一是已知中给出的,二是图形中隐含的(如公共边,公共角、对顶角、邻补角、外角、平角等)
所以找条件归结成两句话:已知中找,图形中看.
2.在△ABC和△A1B1C1中,已知AB=A1B1,
∠A=∠A1,若要△ABC≌△A1B1C1,
还需要 ( )
A.∠B=∠B1 B.∠C=∠C1
C.以上全对
3.如图所示,已知∠BDC=∠ACD,∠ADB=∠BCA,
△ADC与△BCD全等吗?为什么?
【当堂达标】
1.如图所示,∠1=∠2,∠C=∠E,AB=AD
BC和DE相等吗?为什么?
2.如图:AE∥BF,AD=BC,∠FDB=∠ECA,请判断△ACE与△BDF全等吗?为什么?
3.如图AB=AC,若使△AEB≌△ADC, 则还需要什么条件?
补充上条件后,并说明理由。
【巩固训练】
1.已知AB∥DE,BC∥EF,D、C在AF上,且AD=CF。
试说明△ABC与△DEF全等.
2.如图.A、B、C、D在同一直线上,EA∥FB, EC∥FD, EC=FD,
试说明AB=CD
3.如图:D是△ABC边AC上一点,DF交AB于E,且DE=EF,又FB∥AC。
试说明AE=BE
8.3 怎样判断三角形全等(1)
【学习目标】1.熟记角边角公理、角角边推论的内容;
2.知道能角边角公理及其推论证明两个三角形全等。
【课前预习】
学习任务一:
(1)如图1所示,图中两个三角形能够完全重合,下面写法中正确的是( )
A.△ABE≌△AFB B.△ABE≌△ABF C.△ABE≌△FBA D.△ABE≌△FAB
图1 图2
(2)如图2所示,△ABC≌△CDA,并且AB=CD,下列结论中错误的是( )
A.∠1=∠2 B.AC=CA C.∠D=∠B D.AC=BC
学习任务二:
通过P28实验与探究你得到的结论是
判定1:(角边角判定):
应用格式:
练习:如图,已知∠C=∠E,AC=AE
试说明 △ABC≌△ADE
学习任务三:
改变公理1的条件:有两角和其中一角的对边对应相等,
这样的两个三角形是否全等呢?
如图,已知∠FAB=∠EAB,∠F=∠E △ABF与△ABE
全等吗?为什么?
推论: (角角边判定)
(注意区别“对应边和对边”)
【课中探究】
问题一:阅读教材第28—29页内容,思考并总结本节课学习的主要内容是什么?
问题二:
1.如图:已知M是△ABC的边BC上一点,
BE∥CF,BE=CF.试说明△BEM≌△CFM
强调:①格式要求:先指出在哪两个三角形中;再按公理顺序列出三个条件,并用括号把它们括在一起;写出结论.
②在应用时,怎样寻找已知条件:已知条件包含两部分,一是已知中给出的,二是图形中隐含的(如公共边,公共角、对顶角、邻补角、外角、平角等)
所以找条件归结成两句话:已知中找,图形中看.
2.在△ABC和△A1B1C1中,已知AB=A1B1,
∠A=∠A1,若要△ABC≌△A1B1C1,
还需要 ( )
A.∠B=∠B1 B.∠C=∠C1
C.以上全对
3.如图所示,已知∠BDC=∠ACD,∠ADB=∠BCA,
△ADC与△BCD全等吗?为什么?
【当堂达标】
1.如图所示,∠1=∠2,∠C=∠E,AB=AD
BC和DE相等吗?为什么?
2.如图:AE∥BF,AD=BC,∠FDB=∠ECA,请判断△ACE与△BDF全等吗?为什么?
3.如图AB=AC,若使△AEB≌△ADC, 则还需要什么条件?
补充上条件后,并说明理由。
【巩固训练】
1.已知AB∥DE,BC∥EF,D、C在AF上,且AD=CF。
试说明△ABC与△DEF全等.
2.如图.A、B、C、D在同一直线上,EA∥FB, EC∥FD, EC=FD,
试说明AB=CD
3.如图:D是△ABC边AC上一点,DF交AB于E,且DE=EF,又FB∥AC。
试说明AE=BE
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
