八年级数学(下)学案案(第十一章)11.5几何证明举例(第3课时)
文档属性
| 名称 | 八年级数学(下)学案案(第十一章)11.5几何证明举例(第3课时) |
|
|
| 格式 | zip | ||
| 文件大小 | 39.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-22 00:00:00 | ||
图片预览

文档简介
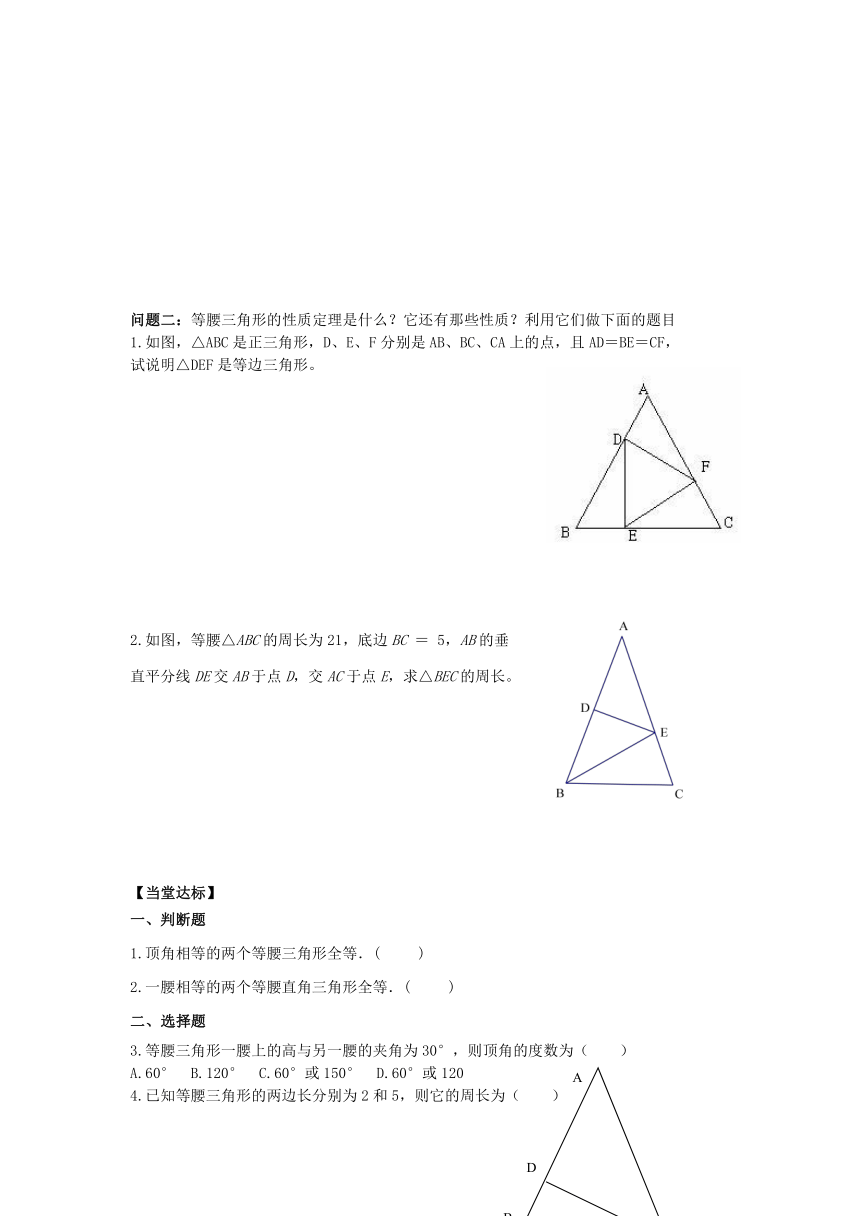
八年级数学(下)学案案(第十一章)
11.5几何证明举例(第3课时)
【学习目标】1.根据三角形全等推导等腰三角形的性质; 2.掌握等腰三角形的性质定理。
【课前预习】
预习课本第132-134页内容,解答下面的问题:
(一)交流与发现 (1)“等腰三角形的两个底角相等”是真命题吗?怎样证明?
(2)说出命题“等腰三角形的两个底角相等”的逆命题?
(3)这个逆命题是真命题吗?怎样证明它的正确性?
(二)探究新知 在右图等腰△ABC中,AB=AC,AD⊥BC.∠1与∠2有什么关系?
BD与CD有什么关系?你能得出什么结论?试着总结一下。
等腰三角形性质定理:
(三)练习
1.已知:如图,点D,E在BC上,AB=AC,AD=AE,求证:BD=CE
【课中导学】
问题一:如图,AD是等腰△ABC的底边上的高,
DE⊥AB于E,DF⊥AC于F.
图中有哪几组相等的线段?
你知道它们为什么相等吗?说出理由.
问题二:等腰三角形的性质定理是什么?它还有那些性质?利用它们做下面的题目
1.如图,△ABC是正三角形,D、E、F分别是AB、BC、CA上的点,且AD=BE=CF,
试说明△DEF是等边三角形。
2.如图,等腰△ABC的周长为21,底边BC = 5,AB的垂
直平分线DE交AB于点D,交AC于点E,求△BEC的周长。
【当堂达标】
一、判断题
1.顶角相等的两个等腰三角形全等.( )
2.一腰相等的两个等腰直角三角形全等.( )
二、选择题
3.等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为( )
A.60° B.120° C.60°或150° D.60°或120
4.已知等腰三角形的两边长分别为2和5,则它的周长为( )
A.12或9 B.12 C.9 D.7
5.如图,等腰三角形ABC中,AB=AC,∠A=44°,
CD⊥AB于D,则∠DCB等于( )
A.44° B.68°
C.46° D.22°
三、解答题
6.如图,已知AB=AC,∠A=40°,AB的垂直平分线交AC于D,求∠DBC的度数.
7.已知:如图,△ABC是等边三角形,DE∥BC,分别
交AB、AC于点D、E。求证:△ADE是等边三角形。
【巩固训练】
一、 选择题
1.已知:如图,在△ABC中,AB=AC,BC=BD,AD=DE=EB,则∠A的度数是( )
A.30° B.36° C.45° D.54°
2.如图,等边△ABC中,BD=CE,AD与BE
相交于点P,则∠APE的度数是( )
A.45° B.55° C.60° D.75°
3.如图,△ABC是等边三角形,BD是中线,
延长BC到E,使CE=CD,则下列结论正确的是( )
A.△CDE是等边三角形 B.DE=AB
C.点D在线段BE的垂直平分线上
D.点D在AB的垂直平分线上
4.△ABC中,AB=BD=AC,AD=CD,则∠ADB的度数是( )
A.36° B.45° C.60° D.72°
5.如图,△ABC是等边三角形,AD是高,并且AB恰
好是DE的垂直平分线,则下列结论正确的是( )
A.△ABC≌△AED B.△AED是等边三角形
C.∠EAB=60° D.AD>DE
二、解答题
1.已知:如图,在△ABC中,BF平分∠ABC,CF平分∠ACB,∠A=65°,
求:∠BFC的大小
2.已知:如图 , DN=EM , 且DN⊥AB于D , EM⊥AC于E ,BM=CN
求证:∠B=∠C
11.5几何证明举例(第3课时)
【学习目标】1.根据三角形全等推导等腰三角形的性质; 2.掌握等腰三角形的性质定理。
【课前预习】
预习课本第132-134页内容,解答下面的问题:
(一)交流与发现 (1)“等腰三角形的两个底角相等”是真命题吗?怎样证明?
(2)说出命题“等腰三角形的两个底角相等”的逆命题?
(3)这个逆命题是真命题吗?怎样证明它的正确性?
(二)探究新知 在右图等腰△ABC中,AB=AC,AD⊥BC.∠1与∠2有什么关系?
BD与CD有什么关系?你能得出什么结论?试着总结一下。
等腰三角形性质定理:
(三)练习
1.已知:如图,点D,E在BC上,AB=AC,AD=AE,求证:BD=CE
【课中导学】
问题一:如图,AD是等腰△ABC的底边上的高,
DE⊥AB于E,DF⊥AC于F.
图中有哪几组相等的线段?
你知道它们为什么相等吗?说出理由.
问题二:等腰三角形的性质定理是什么?它还有那些性质?利用它们做下面的题目
1.如图,△ABC是正三角形,D、E、F分别是AB、BC、CA上的点,且AD=BE=CF,
试说明△DEF是等边三角形。
2.如图,等腰△ABC的周长为21,底边BC = 5,AB的垂
直平分线DE交AB于点D,交AC于点E,求△BEC的周长。
【当堂达标】
一、判断题
1.顶角相等的两个等腰三角形全等.( )
2.一腰相等的两个等腰直角三角形全等.( )
二、选择题
3.等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为( )
A.60° B.120° C.60°或150° D.60°或120
4.已知等腰三角形的两边长分别为2和5,则它的周长为( )
A.12或9 B.12 C.9 D.7
5.如图,等腰三角形ABC中,AB=AC,∠A=44°,
CD⊥AB于D,则∠DCB等于( )
A.44° B.68°
C.46° D.22°
三、解答题
6.如图,已知AB=AC,∠A=40°,AB的垂直平分线交AC于D,求∠DBC的度数.
7.已知:如图,△ABC是等边三角形,DE∥BC,分别
交AB、AC于点D、E。求证:△ADE是等边三角形。
【巩固训练】
一、 选择题
1.已知:如图,在△ABC中,AB=AC,BC=BD,AD=DE=EB,则∠A的度数是( )
A.30° B.36° C.45° D.54°
2.如图,等边△ABC中,BD=CE,AD与BE
相交于点P,则∠APE的度数是( )
A.45° B.55° C.60° D.75°
3.如图,△ABC是等边三角形,BD是中线,
延长BC到E,使CE=CD,则下列结论正确的是( )
A.△CDE是等边三角形 B.DE=AB
C.点D在线段BE的垂直平分线上
D.点D在AB的垂直平分线上
4.△ABC中,AB=BD=AC,AD=CD,则∠ADB的度数是( )
A.36° B.45° C.60° D.72°
5.如图,△ABC是等边三角形,AD是高,并且AB恰
好是DE的垂直平分线,则下列结论正确的是( )
A.△ABC≌△AED B.△AED是等边三角形
C.∠EAB=60° D.AD>DE
二、解答题
1.已知:如图,在△ABC中,BF平分∠ABC,CF平分∠ACB,∠A=65°,
求:∠BFC的大小
2.已知:如图 , DN=EM , 且DN⊥AB于D , EM⊥AC于E ,BM=CN
求证:∠B=∠C
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
