2013年高考数学(课标版)原创预测题(理科):专题六 统计与概率、推理与证明、算法初步
文档属性
| 名称 | 2013年高考数学(课标版)原创预测题(理科):专题六 统计与概率、推理与证明、算法初步 |  | |
| 格式 | zip | ||
| 文件大小 | 411.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-22 15:39:38 | ||
图片预览




文档简介
新课标理 专题六 统计与概率、推理与证明、算法初步
一、选择题
1、2011年3月11日,日本发生了9级大地震并引发了核泄漏.某商场有四类食品,粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种,现从中抽取一个容量为20的样本进行食品安全检测.若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是( )
.4 .5 .6 .7
2、设随机变量服从标准正态分布,已知=0.950,则( )
.0.025 .0.050 .0.950 .0.975
3.设是三条不同的直线,是三个不同的平面,是三个不同的向量,则下列命题不正确的是( )
.若∥,∥,则∥ .若∥,∥,则∥
.若∥,∥,则∥ .若∥,∥,则不一定平行于
4、温家宝总理在十二五规划中提到十二五期间,要保民生,为落实温总理指示,某社区办事处为了调查居民的身体素质情况,从本社区内随机抽查了50名居民进行百米测试,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:
组别
第一组
第二组
第三组
第四组
第五组
第六组
成绩(秒)
[13,14
[14,15
[15,16
[16,17
[17,18
[18,,
右图是按上述分组方法得到的频率分布直方图. 设成绩小于17秒
的居民人数占抽查人数的百分比为,成绩大于等于
15秒且小于17秒的居民人数为,则从频率分布直方
图中可以分析出和分别为( )
. .
. .
5.在区域内任意取一点,则的概率是( )
.0 . . .
6、十六届亚运会于2010年11月12日至27日在广州隆重召开,吉祥物“祥和如意乐洋洋”,寓意着“吉祥、和谐、幸福、圆满和快乐”,深受人们的喜爱!
每套吉祥物含有5只小羊,小明有一套吉祥物,他想将这5只小羊全发给4名同学,每名同学至少有一只羊的概率是 . . . .
7.若函数,,其中的定义域为R,且不恒为零,则( )
.均为偶函数 .为奇函数,为偶函数
.与均为奇函数 .为偶函数,为奇函数
8.设函数,类比课本中推导等差数列前项和公式的方法,可求得的值为( )
. .
. .
9、位于坐标原点的一个质点P按下述规则移动:质点每次移动一个单位;移动的方向为向上或向右,并且向上、向右移动的概率都是.质点P 移动5次后位于点的概率为( )
. . . .
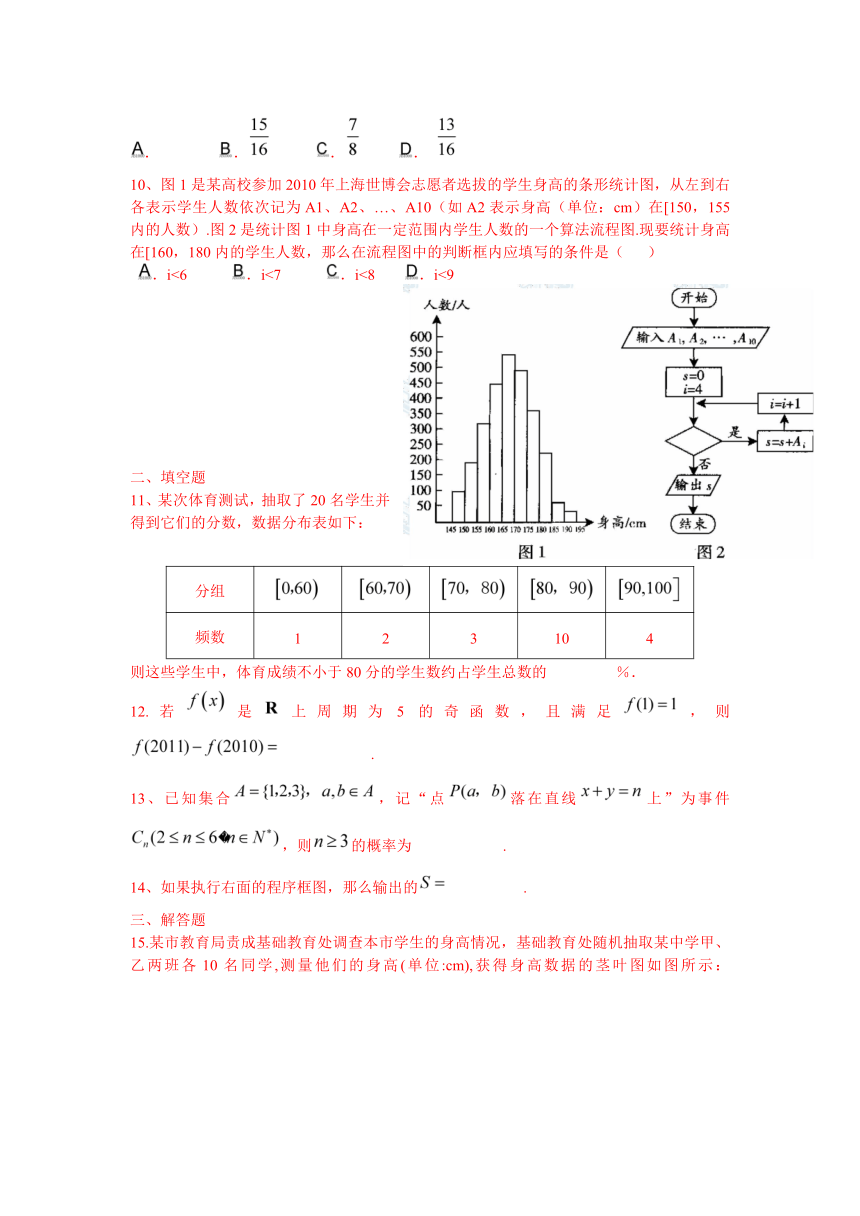
10、图1是某高校参加2010年上海世博会志愿者选拔的学生身高的条形统计图,从左到右各表示学生人数依次记为A1、A2、…、A10(如A2表示身高(单位:cm)在[150,155内的人数).图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在[160,180内的学生人数,那么在流程图中的判断框内应填写的条件是( )
.i<6 .i<7 .i<8 .i<9
二、填空题
11、某次体育测试,抽取了20名学生并得到它们的分数,数据分布表如下:
分组
频数
1
2
3
10
4
则这些学生中,体育成绩不小于80分的学生数约占学生总数的 %.
12.若是上周期为5的奇函数,且满足,则 .
13、已知集合,记“点落在直线上”为事件,则的概率为 .
14、如果执行右面的程序框图,那么输出的 .
三、解答题
15.某市教育局责成基础教育处调查本市学生的身高情况,基础教育处随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示:
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
16、某地质监部门检查食品类产品情况,从某批产品中,有放回地抽取产品两次,每次随机抽取1件,假设事件:“取出的2件产品中至多有1件是二等品”的概率.
(1)求从该批产品中任取1件是二等品的概率;
(2)若该批产品共100件,从中任意抽取2件,表示取出的2件产品中二等品的件数,求的分布列.
17.已知函数,
(1)分别求的值;
(2)归纳猜想一般性结论,并给出证明;
(3)求值:
18. 对于定义域为的函数,如果同时满足以下三条:①对任意的,总有;
②;③若,都有成立,则称函数为理想函数.
(1)若函数为理想函数,证明
(2)判断函数()是否为理想函数,如果是,请予以证明;如果不是,请说明理由.
19.以下是鲁西南地区某县搜集到的新房屋的销售价格和房屋的面积的数据:
(1)画出数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线;
(3)据(2)的结果估计当房屋面积为时的销售价格
20.某项选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考试,否则即被淘汰,已知某选手能正确回答第一、二、三轮的问题的概率分别为、、,且各轮问题能否正确回答互不影响. (Ⅰ)求该选手被淘汰的概率;
(Ⅱ)该选手在选拔中回答问题的个数记为ξ,求随机变量ξ的分布列与数学期望.(注:本小题结果可用分数表示)
答案解析(专题六)新课标理
1.选 共有食品100种,抽取容量为20的样本,各抽取,故抽取植物油类与果蔬类食品种数之和为2+4=6,选.
2.选A 因为服从标准正态分布,
.
3.选.直线、平面的平行具有传递性,故、正确,向量的平行不具有传递性,如果,则, 不正确,故选.
4.选 从频率分布直方图上可以看出
,.
5.选 如图,的概率为=.
根据对立事件概率公式,的概率是.
6.选 将5只不同的小羊全发给4名同学共有45种发法,其中每名同学至少有一只羊的发法有,故每名同学至少有一只羊的概率是P=,选.
7.选 ,,故选.
8.选 ,∴,
,
发现正好是一个定值,
.
9.选 质点P移动5次后可能位于点,其中满足点为,其对立事件为质点P 移动5次后位于点,
即质点在移动过程中向右移动5次、向上移动0次或向右移动0次、向上移动5次,因此所求的概率为.
10.选 因为S=,故选.
11. 【解析】 由表中可知这些学生中,体育成绩不小于80分的学生数为:,
故约占学生总数的.
答案:70
12. 【解析】若是上周期为5的奇函数,则
.
答案:1
13. 【解析】方法1:事件的总的基本事件个数为.
当n=3时,落在直线上的点为(1,2)、(2,1),含有2个基本事件;
当n=4时,落在直线上的点为(1,3)、(2,2)、(3,1),含有3个基本事件;
当n=5时,落在直线上的点为(2,3)、(3,2),含有2个基本事件;
当n=6时,落在直线上的点为(3,3),含有1个基本事件;
故的概率为
方法2:当n=2时,落在直线上的点为(1,1), 含有1个基本事件,
故的概率为
答案:
14. 【解析】由程序知,
答案:2500
15.【解析】(1)由茎叶图可知:乙班平均身高较高;
(2)
甲班的样本方差为
(3)设身高为176cm的同学被抽中的事件为.
从乙班10名同学中抽中两名身高不低于173cm的同学有:(181,173),(181,176),(181,178),(181,179),(179,173),(179,176),(179,178),(178,173),(178, 176) ,(176,173)共10个基本事件,而事件含有4个基本事件, .
16.【解析】(1)记表示事件“取出的2件产品中无二等品”,
表示事件“取出的2件产品中恰有1件二等品”.
则互斥,且,故
于是.
解得(舍去).
所以所求概率.
(2)的可能取值为.
若该批产品共100件,由(1)知其二等品有件,故
.
.
.
所以的分布列为
0
1
2
18.【解析】(1)取可得
.
又由条件①可得,故.
(2)是理想函数,显然在[0,1]满足条件①;
也满足条件②,若,,,则
,
即满足条件③, 故是理想函数.
19.【解析】(1)数据对应的散点图如图所示:
(2),,
,
设所求回归直线方程为,
则,
,
故所求回归直线方程为.
(3)据(2),当时,销售价格的估计值为:
(万元).
20.方法一:(Ⅰ)记“该选手能正确回答第轮的问题”的事件为,则,,,
该选手被淘汰的概率
.
(Ⅱ)的可能值为,,
,
.
的分布列为
1
2
3
.
方法二:(Ⅰ)记“该选手能正确回答第轮的问题”的事件为,则,,.
该选手被淘汰的概率
.
(Ⅱ)同方法一.
一、选择题
1、2011年3月11日,日本发生了9级大地震并引发了核泄漏.某商场有四类食品,粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种,现从中抽取一个容量为20的样本进行食品安全检测.若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是( )
.4 .5 .6 .7
2、设随机变量服从标准正态分布,已知=0.950,则( )
.0.025 .0.050 .0.950 .0.975
3.设是三条不同的直线,是三个不同的平面,是三个不同的向量,则下列命题不正确的是( )
.若∥,∥,则∥ .若∥,∥,则∥
.若∥,∥,则∥ .若∥,∥,则不一定平行于
4、温家宝总理在十二五规划中提到十二五期间,要保民生,为落实温总理指示,某社区办事处为了调查居民的身体素质情况,从本社区内随机抽查了50名居民进行百米测试,成绩全部介于13秒与19秒之间,将测试结果按如下方式分成六组:
组别
第一组
第二组
第三组
第四组
第五组
第六组
成绩(秒)
[13,14
[14,15
[15,16
[16,17
[17,18
[18,,
右图是按上述分组方法得到的频率分布直方图. 设成绩小于17秒
的居民人数占抽查人数的百分比为,成绩大于等于
15秒且小于17秒的居民人数为,则从频率分布直方
图中可以分析出和分别为( )
. .
. .
5.在区域内任意取一点,则的概率是( )
.0 . . .
6、十六届亚运会于2010年11月12日至27日在广州隆重召开,吉祥物“祥和如意乐洋洋”,寓意着“吉祥、和谐、幸福、圆满和快乐”,深受人们的喜爱!
每套吉祥物含有5只小羊,小明有一套吉祥物,他想将这5只小羊全发给4名同学,每名同学至少有一只羊的概率是 . . . .
7.若函数,,其中的定义域为R,且不恒为零,则( )
.均为偶函数 .为奇函数,为偶函数
.与均为奇函数 .为偶函数,为奇函数
8.设函数,类比课本中推导等差数列前项和公式的方法,可求得的值为( )
. .
. .
9、位于坐标原点的一个质点P按下述规则移动:质点每次移动一个单位;移动的方向为向上或向右,并且向上、向右移动的概率都是.质点P 移动5次后位于点的概率为( )
. . . .
10、图1是某高校参加2010年上海世博会志愿者选拔的学生身高的条形统计图,从左到右各表示学生人数依次记为A1、A2、…、A10(如A2表示身高(单位:cm)在[150,155内的人数).图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在[160,180内的学生人数,那么在流程图中的判断框内应填写的条件是( )
.i<6 .i<7 .i<8 .i<9
二、填空题
11、某次体育测试,抽取了20名学生并得到它们的分数,数据分布表如下:
分组
频数
1
2
3
10
4
则这些学生中,体育成绩不小于80分的学生数约占学生总数的 %.
12.若是上周期为5的奇函数,且满足,则 .
13、已知集合,记“点落在直线上”为事件,则的概率为 .
14、如果执行右面的程序框图,那么输出的 .
三、解答题
15.某市教育局责成基础教育处调查本市学生的身高情况,基础教育处随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示:
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
16、某地质监部门检查食品类产品情况,从某批产品中,有放回地抽取产品两次,每次随机抽取1件,假设事件:“取出的2件产品中至多有1件是二等品”的概率.
(1)求从该批产品中任取1件是二等品的概率;
(2)若该批产品共100件,从中任意抽取2件,表示取出的2件产品中二等品的件数,求的分布列.
17.已知函数,
(1)分别求的值;
(2)归纳猜想一般性结论,并给出证明;
(3)求值:
18. 对于定义域为的函数,如果同时满足以下三条:①对任意的,总有;
②;③若,都有成立,则称函数为理想函数.
(1)若函数为理想函数,证明
(2)判断函数()是否为理想函数,如果是,请予以证明;如果不是,请说明理由.
19.以下是鲁西南地区某县搜集到的新房屋的销售价格和房屋的面积的数据:
(1)画出数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线;
(3)据(2)的结果估计当房屋面积为时的销售价格
20.某项选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考试,否则即被淘汰,已知某选手能正确回答第一、二、三轮的问题的概率分别为、、,且各轮问题能否正确回答互不影响. (Ⅰ)求该选手被淘汰的概率;
(Ⅱ)该选手在选拔中回答问题的个数记为ξ,求随机变量ξ的分布列与数学期望.(注:本小题结果可用分数表示)
答案解析(专题六)新课标理
1.选 共有食品100种,抽取容量为20的样本,各抽取,故抽取植物油类与果蔬类食品种数之和为2+4=6,选.
2.选A 因为服从标准正态分布,
.
3.选.直线、平面的平行具有传递性,故、正确,向量的平行不具有传递性,如果,则, 不正确,故选.
4.选 从频率分布直方图上可以看出
,.
5.选 如图,的概率为=.
根据对立事件概率公式,的概率是.
6.选 将5只不同的小羊全发给4名同学共有45种发法,其中每名同学至少有一只羊的发法有,故每名同学至少有一只羊的概率是P=,选.
7.选 ,,故选.
8.选 ,∴,
,
发现正好是一个定值,
.
9.选 质点P移动5次后可能位于点,其中满足点为,其对立事件为质点P 移动5次后位于点,
即质点在移动过程中向右移动5次、向上移动0次或向右移动0次、向上移动5次,因此所求的概率为.
10.选 因为S=,故选.
11. 【解析】 由表中可知这些学生中,体育成绩不小于80分的学生数为:,
故约占学生总数的.
答案:70
12. 【解析】若是上周期为5的奇函数,则
.
答案:1
13. 【解析】方法1:事件的总的基本事件个数为.
当n=3时,落在直线上的点为(1,2)、(2,1),含有2个基本事件;
当n=4时,落在直线上的点为(1,3)、(2,2)、(3,1),含有3个基本事件;
当n=5时,落在直线上的点为(2,3)、(3,2),含有2个基本事件;
当n=6时,落在直线上的点为(3,3),含有1个基本事件;
故的概率为
方法2:当n=2时,落在直线上的点为(1,1), 含有1个基本事件,
故的概率为
答案:
14. 【解析】由程序知,
答案:2500
15.【解析】(1)由茎叶图可知:乙班平均身高较高;
(2)
甲班的样本方差为
(3)设身高为176cm的同学被抽中的事件为.
从乙班10名同学中抽中两名身高不低于173cm的同学有:(181,173),(181,176),(181,178),(181,179),(179,173),(179,176),(179,178),(178,173),(178, 176) ,(176,173)共10个基本事件,而事件含有4个基本事件, .
16.【解析】(1)记表示事件“取出的2件产品中无二等品”,
表示事件“取出的2件产品中恰有1件二等品”.
则互斥,且,故
于是.
解得(舍去).
所以所求概率.
(2)的可能取值为.
若该批产品共100件,由(1)知其二等品有件,故
.
.
.
所以的分布列为
0
1
2
18.【解析】(1)取可得
.
又由条件①可得,故.
(2)是理想函数,显然在[0,1]满足条件①;
也满足条件②,若,,,则
,
即满足条件③, 故是理想函数.
19.【解析】(1)数据对应的散点图如图所示:
(2),,
,
设所求回归直线方程为,
则,
,
故所求回归直线方程为.
(3)据(2),当时,销售价格的估计值为:
(万元).
20.方法一:(Ⅰ)记“该选手能正确回答第轮的问题”的事件为,则,,,
该选手被淘汰的概率
.
(Ⅱ)的可能值为,,
,
.
的分布列为
1
2
3
.
方法二:(Ⅰ)记“该选手能正确回答第轮的问题”的事件为,则,,.
该选手被淘汰的概率
.
(Ⅱ)同方法一.
同课章节目录
