2013年高考数学(课标版)原创预测题(理科):专题四 立体几何
文档属性
| 名称 | 2013年高考数学(课标版)原创预测题(理科):专题四 立体几何 |  | |
| 格式 | zip | ||
| 文件大小 | 355.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-22 15:39:59 | ||
图片预览


文档简介
新课标理科 专题四 立体几何
一、选择题
1.设三条射线PA、PB、PC两两所成的角都是60度,则直线PC与平面PAB所成的角的余弦值为( )
() () () ()
2.一个圆柱的轴截面为正方形,其体积与一个球的体积之比是3:2,则这个圆柱的表面积与这个球的表面积之比为( )
()1:1 () 1: () : () 3:2
已知两条不同的直线、,两个不同的平面、,则下列命题中的真命题是( )
若,,,则()若,∥,,则
()若∥,∥,∥,则∥()若∥,,,则∥
在直三棱柱ABC-A1B1C1中,BC⊥CA,点D1、F1分别是A1B1、A1C1的中点,若BC=CA=CC1,则异面直线BD1与AF1所成角的余弦值为( )
某个数学活动小组为了测量学校操场上国旗旗杆DC的高度,在旗杆的正西方向的点A测得旗杆顶端D的仰角为30度,沿点A向北偏东60度前进18米到达B点,测得旗杆顶端D的仰角为45度,经目测AB小于AC,则旗杆的高度为( )
()9米 ()16米 ()18米 ()9米或18米
如图是一个六棱柱的三视图,俯视图是一个周长为3的正六边形,该六棱柱的顶点都在同一个球面上,那么这个球的体积为( )
() () ()
7.等边三角形ABC的边长为4,M、N分别为AB、AC的中点,沿MN将△AMN折起,使得平面AMN与平面MNCB所成的二面角为30°,则四棱锥A—MNCB的体积为 ( )
() () () ()3
8.二面角的平面角为,在内,于B,AB=2,在内,于D,CD=3,BD=1, M是棱上的一个动点,则AM+CM的最小值为( )
() () () () 是的函数
9.设为两两不重合的平面,为两两不重合的直线.给出下列四个命题:①若,则;②若,则;③若,,则;④若,则,其中真命题的个数是 ( )
()1 ()2 ()3 ()4?
10.矩形ABCD中,AB=4,BC=2,E、F分别为AB、CD的中点,沿EF把BCFE折起后与ADFE垂直,P为矩形ADFE内一动点,P到平面BCFE的距离与它到点A的距离相等,设动点P的轨迹是曲线L,则曲线L把矩形ADFE分成的两部分的面积比为( )
()1:1 ()2:3 ()1:2 ()1:4
二、填空题
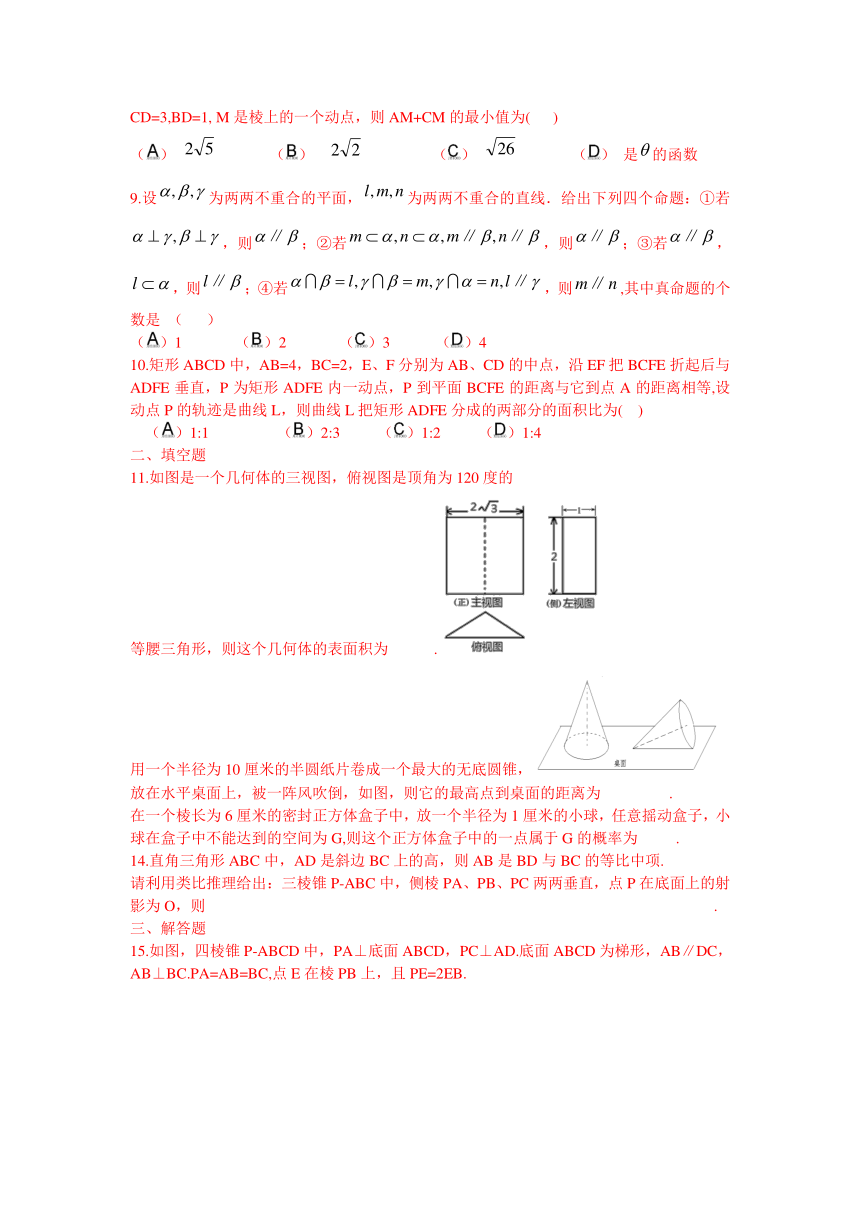
11.如图是一个几何体的三视图,俯视图是顶角为120度的
等腰三角形,则这个几何体的表面积为 .
用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥,
放在水平桌面上,被一阵风吹倒,如图,则它的最高点到桌面的距离为 .
在一个棱长为6厘米的密封正方体盒子中,放一个半径为1厘米的小球,任意摇动盒子,小球在盒子中不能达到的空间为G,则这个正方体盒子中的一点属于G的概率为 .
14.直角三角形ABC中,AD是斜边BC上的高,则AB是BD与BC的等比中项.
请利用类比推理给出:三棱锥P-ABC中,侧棱PA、PB、PC两两垂直,点P在底面上的射影为O,则 .
三、解答题
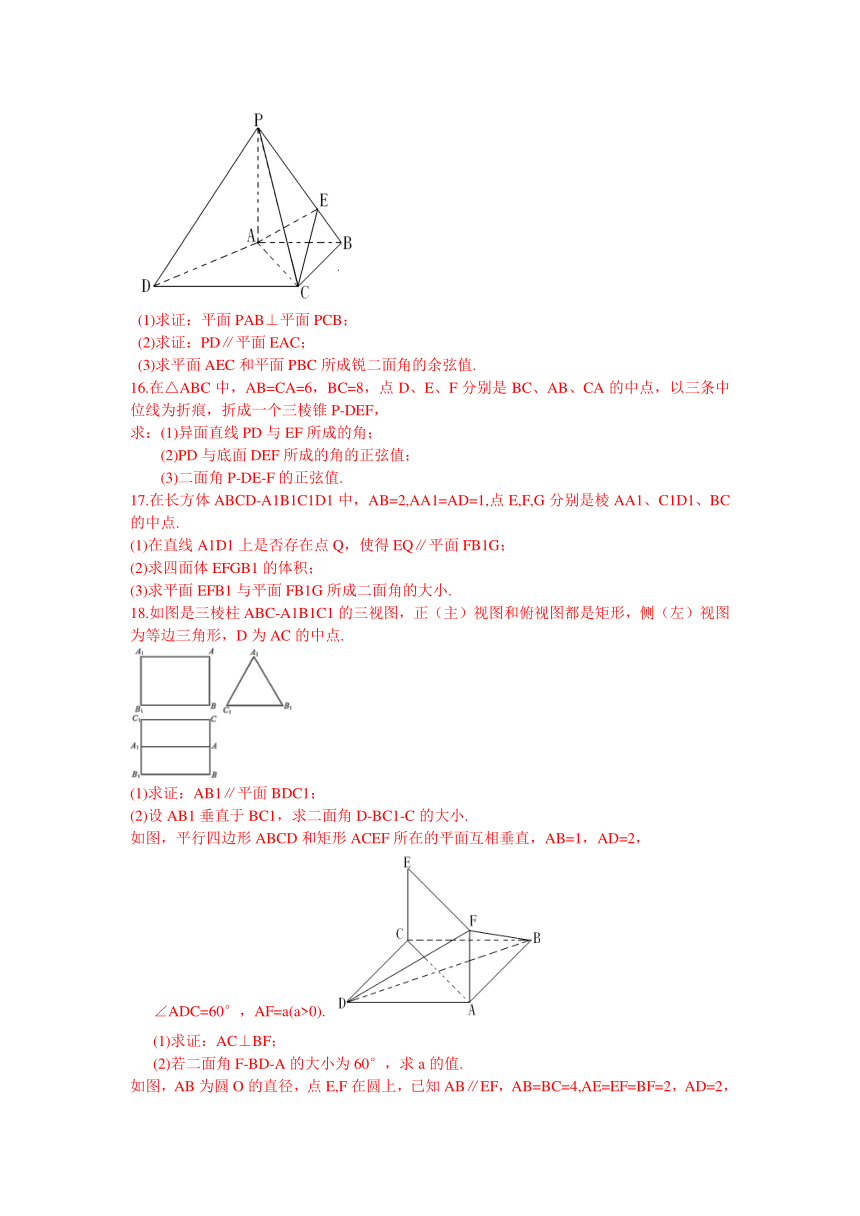
15.如图,四棱锥P-ABCD中,PA⊥底面ABCD,PC⊥AD.底面ABCD为梯形,AB∥DC,
AB⊥BC.PA=AB=BC,点E在棱PB上,且PE=2EB.
(1)求证:平面PAB⊥平面PCB;
(2)求证:PD∥平面EAC;
(3)求平面AEC和平面PBC所成锐二面角的余弦值.
16.在△ABC中,AB=CA=6,BC=8,点D、E、F分别是BC、AB、CA的中点,以三条中位线为折痕,折成一个三棱锥P-DEF,
求:(1)异面直线PD与EF所成的角;
(2)PD与底面DEF所成的角的正弦值;
(3)二面角P-DE-F的正弦值.
17.在长方体ABCD-A1B1C1D1中,AB=2,AA1=AD=1,点E,F,G分别是棱AA1、C1D1、BC的中点.
(1)在直线A1D1上是否存在点Q,使得EQ∥平面FB1G;
(2)求四面体EFGB1的体积;
(3)求平面EFB1与平面FB1G所成二面角的大小.
18.如图是三棱柱ABC-A1B1C1的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,D为AC的中点.
(1)求证:AB1∥平面BDC1;
(2)设AB1垂直于BC1,求二面角D-BC1-C的大小.
如图,平行四边形ABCD和矩形ACEF所在的平面互相垂直,AB=1,AD=2,
∠ADC=60°,AF=a(a>0).
(1)求证:AC⊥BF;
(2)若二面角F-BD-A的大小为60°,求a的值.
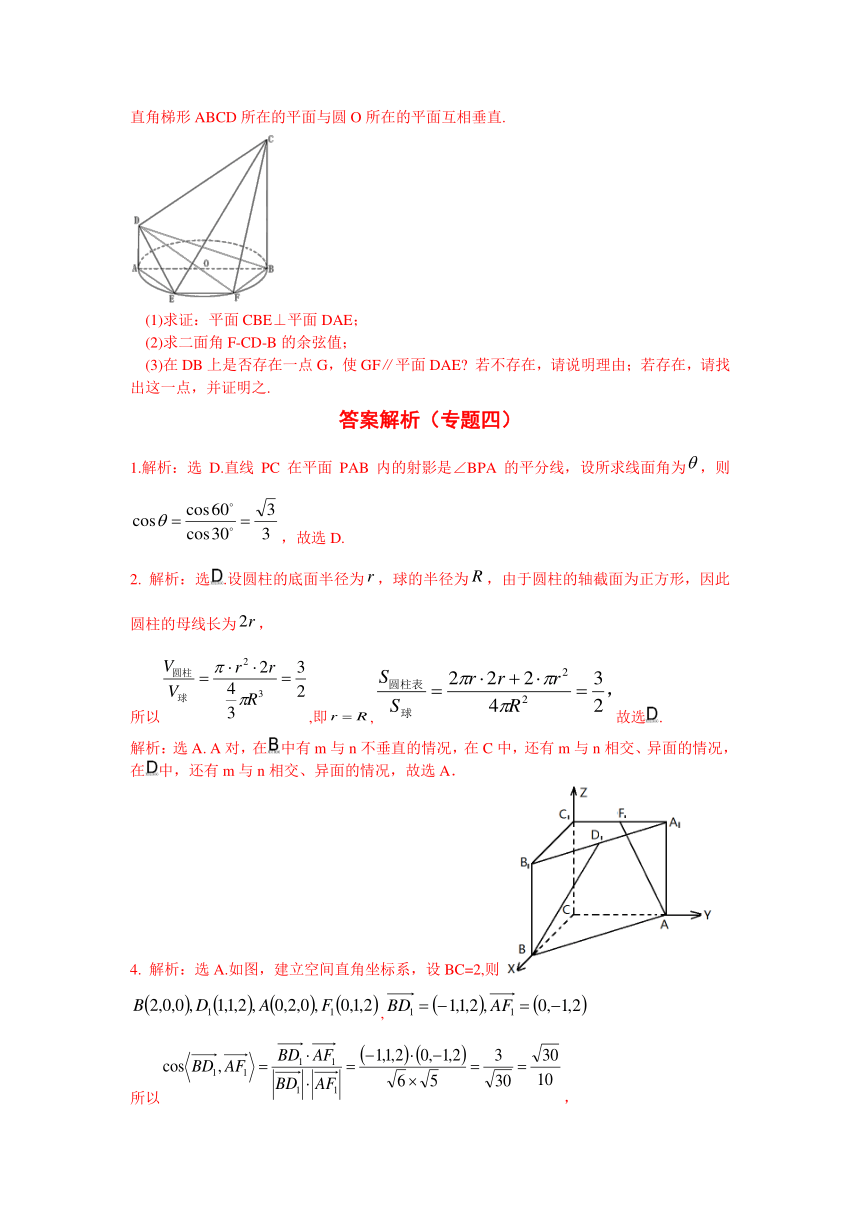
如图,AB为圆O的直径,点E,F在圆上,已知AB∥EF,AB=BC=4,AE=EF=BF=2,AD=2,直角梯形ABCD所在的平面与圆O所在的平面互相垂直.
(1)求证:平面CBE⊥平面DAE;
(2)求二面角F-CD-B的余弦值;
(3)在DB上是否存在一点G,使GF∥平面DAE 若不存在,请说明理由;若存在,请找出这一点,并证明之.
答案解析(专题四)
1.解析:选D.直线PC在平面PAB内的射影是∠BPA的平分线,设所求线面角为,则,故选D.
2. 解析:选.设圆柱的底面半径为,球的半径为,由于圆柱的轴截面为正方形,因此圆柱的母线长为,
所以,即,故选.
解析:选A. A对,在中有m与n不垂直的情况,在C中,还有m与n相交、异面的情况,在中,还有m与n相交、异面的情况,故选A.
4. 解析:选A.如图,建立空间直角坐标系,设BC=2,则
,
所以,
所以异面直线BD1与F1所成角的余弦值为,故选.
5. 解析:选C.如图,设,则,
,所以在中,
应用余弦定理得,
解这个方程得,
当时,,与已知矛盾,故舍去.当时符合题意,所以选C.
6. 解析:选.这是一个正六棱柱,上下两个底面的中心连线的中点就是球心,
因为六棱柱的高为,所以球心到底面的距离为.
因为底面正六边形的周长为3,所以底面正六边形的边长为,
即底面外接圆的半径为,由球的截面性质得球半径,
所以这个球的体积为,故选.
解析:选 .在平面图中,过A作AL⊥BC,交MN于K,交BC于L.则AK⊥MN,KL⊥MN.
∴∠AKL是面AMN与面MNCB所成的二面角的平面角,即有∠AKL=30°.
则四棱锥A—MNCB的高h==.=.
∴ =.故选 A.
8.解析:选C.如图,把平面展开到内成一个平面,连接AC,交于M,此时AM+CM=AC,过C作CN垂直于AB的延长线,垂足为N,则.故选C.
9. 解析:选.①也有相交的情况;②要保证相交,才有;③由面面平行的性质定理可知正确;④因,同样,从而,故④对.故选.?
10. 解析:选C.如图,过点P作PQ垂直于FE,则PQ垂直于平面BCFE,
所以PQ=PA,所以动点P的轨迹(即曲线L)为以A为焦点,以FE为准线的抛物线在矩形内的部分,在平面ADFE内,取AE中点为R,以R为原点,以RA为x轴,建立平面直角坐标系,则曲线L的方程为,曲线L与线段RA、AD围成的面积为,又矩形ADFE的面积为4,所以曲线L把矩形ADFE分成的两部分的面积比为1:2.故选C.
解析:根据三视图的知识,这个几何体是底面边长分别为的
等腰三角形,高为2的直三棱柱.它的侧面积是,其一个底面的面积为,所以这个三棱柱的表面积为.
答案:
12.解析:要抓住两点:1.半圆纸片的半径成了圆锥的母线,2.半圆弧长成了圆锥的底面周长.设圆锥的底面半径为,母线为,则,,
所以轴截面顶角的一半为,轴截面为正三角形,故圆锥的最高点离桌面的距离为厘米.
答案:厘米
解析:在正方体盒子中,不能到达的八个角的空间即为图一中的内切于正方体的小球不能到达的空间,其体积为.小球沿每条棱运动不能到达的空间(除去两端的两个角)的体积,即为高为4的一个正四棱柱的体积与其内接圆柱体积差的四分之一(如图二),
即,正方体有12条棱,所以在盒子中小球不能到达的空间G的体积为,又正方体盒子的体积为63=216,所这以个正方体盒子中的一点属于G的概率为.
答案:.
14.解析:连接CO,并延长交AB于D,连接PD,
则PD⊥PC,CD⊥AB,所以PD2=DO×DC,所以.即三角形PAB的面积是三角形AOB的面积与三角形ABC的面积的等比中项.
答案:三角形PAB的面积是三角形AOB的面积与三角形ABC的面积的等比中项.
15.解析: (1)∵PA⊥平面ABCD, ∴PA⊥BC.
又AB⊥BC,PAAB=A, ∴ BC⊥平面PAB.
又BC平面PCB,所以平面PAB⊥平面PCB.
(2)∵PA⊥底面ABCD,∴PA⊥AD,又PC⊥AD,PAPC=P,
∴AD⊥平面PAC,∴AC⊥AD.
在梯形ABCD中,由AB⊥BC,AB=BC,得∠BAC=45°,∴∠DCA=∠BAC=45°,
又AC⊥AD,故DAC为等腰直角三角形,
∴DC=AC=(AB)=2AB.
连结BD,交AC于点M,则.
连结EM,在BPD中,,
∴PD∥EM,又EM在平面EAC内,∴PD∥平面EAC.
(3)以A为坐标原点,AB,AP所在直线分别为y轴,z轴,建立如图所示空间直角坐标系.
设PA=AB=BC=a,则A(0,0,0),B(0,a,0),C(a,a,0),P(0,0,a),E.
设=(x,y,1)为平面AEC的一个法向量,
则⊥
∴,解得x=,y=,∴
设为平面PBC的一个法向量,则
又,解得,∴=(0,1,1).
,∴平面AEC和平面PBC所成的锐二面角的余弦值为.
16.解析:(1)取EF的中点N,连接DN、PN,
因为DF=DE,PF=PE,所以PN⊥EF,DN⊥EF,PNDN=N,
所以EF⊥平面PDN,EF⊥PD,所以异面直线PD与EF所成的角为90度.
(2)过点P作PO⊥DN,垂足为O,
由(1)知EF⊥平面PDN,所以平面PDN⊥平面DEF,
所以PO⊥平面DEF,DO是PD在平面DEF上的射影,
∠PDO就是直线PD与平面DEF所成的角.由题意得PN=DN=,PD=4,所以PO=,
所以.
(3)过O作OM⊥DE,垂足为M,连接PM,由(2)知PO⊥DE,又OM⊥DE,OMPO=O,所以DE⊥平面OPM,所以PM⊥DE,
∠PMO就是二面角P-DE-F的平面角.
因为sin∠PMO×sin∠PDM= sin∠PDO,在三角形PDE中,由余弦定理得PM=,
所以sin∠PDM=,所以sin∠PMO=,
所以二面角P-DE-F的正弦值为.
17.解析:如图以D为原点,以DA、DC、DD1所在直线分别为x,y,z轴,建立空间直角坐标系,
则E(1,0,),,,,
(1) 假设存在点Q,使得EQ∥平面FB1G,并设坐标为.
设面的法向量为,则
又,,
∴, 取,
因为∥平面,,
∴ ,∴ ,
故在的延长线上存在点Q,当时,有EQ∥面.
(2),则点E到平面FB1G的距离为
,
因为,
所以,
所以,所以所求的四面体的体积为;(3)设平面EFB1的法向量为,则,
所以,取,
根据两个法向量的方向,可知所求二面角的大小等于两个法向量的夹角的大小,
又因为,所以所求的二面角的大小为90度.
18.解析:
(1)由三视图画出直观图,如图,
这是一个正三棱柱,连接BC1和B1C,交点为O,则O为B1C的中点,连接OD,
因为D为中点,所以OD∥AB1,
又OD在平面BDC1内,AB1不在平面BDC1内,所以AB1∥平面BDC1.
(2)过D作DG⊥BC,垂足为G,连接GO,
因为侧面垂直于底面,所以DG⊥侧面BCC1B1,所以DO在侧面BCC1B1内的射影为GO,
因为AB1垂直于BC1,所以BC1⊥DO,又BC1⊥DG, DGDO=D,所以BC1⊥平面DOG,所以BC1⊥GO,所以∠DOG就是所求的二面角的平面角.
取BC中点F,连接AF,OF,则有OF⊥BC,AF⊥BC,
在直角三角形BOG中,OF⊥BG,
所以,,
故在直角三角形DGO中,DG=OG,∠DOG=450,即所求的二面角的大小为45度.
解析: (1)如图,
在ABC中,∵AB=1,BC=2,∠ABC=60°,
∴由余弦定理得=,
∴,∴∠BAC=90°,即AC⊥AB.
又在矩形ACEF中,AC⊥AF,且AFAB=A,
∴AC⊥平面ABF,又∵BF平面ABF,∴AC⊥BF.
(2)∵平面ACEF⊥平面ABCD,平面ACEF平面ABCD=AC,FA⊥AC,∴FA⊥平面ABCD,
过点A作AG⊥BD于点G,连结FG,则FG⊥BD.
∴∠AGF即是二面角F-BD-A的平面角,∴∠AGF=60°.
在ABD中,由余弦定理得
由
在RtAGF中,∵∠AGF=60°,∴AF=AG·tan∠AGF=
20.解析:(1)如图,
连结BE,因为四边形ABCD是直角梯形,所以AD⊥AB,
又平面ABCD⊥平面ABFE,
所以AD⊥平面ABFE,所以AD⊥BE.
因为AB为圆O的直径,所以AE⊥BE,又AEAD=A,所以BE⊥平面DAE.
又BE平面CBE,所以平面CBE⊥平面DAE.
(2)因为AE=EF=BF=2,连结OE,OF,则OEF是边长为2的等边三角形,以O为原点,OB所在直线为y轴,垂直于OB的直线分别为x轴,z轴,建立如图坐标系,
则有A(0,-2,0),B(0,2,0),C(0,2,4),D(0,-2,2),F(,1,0),
易得平面ABCD的一个法向量为,设平面CDF的一个法向量为因为,
由
所以
结合图形知平面CDF与平面ABCD所成角的余弦值为
存在,点G是BD的中点.
证明:连结OG,GF,则OG∥AD,又因为OG平面DAE,所以OG∥平面DAE,因为AB∥EF,AO=AB=2,EF=2,所以四边形AOFE是平行四边形,所以OF∥AE,又OF平面DAE,所以OF∥平面DAE,又OGOF=O,所以平面OGF∥平面DAE,所以GF∥平面DAE.
一、选择题
1.设三条射线PA、PB、PC两两所成的角都是60度,则直线PC与平面PAB所成的角的余弦值为( )
() () () ()
2.一个圆柱的轴截面为正方形,其体积与一个球的体积之比是3:2,则这个圆柱的表面积与这个球的表面积之比为( )
()1:1 () 1: () : () 3:2
已知两条不同的直线、,两个不同的平面、,则下列命题中的真命题是( )
若,,,则()若,∥,,则
()若∥,∥,∥,则∥()若∥,,,则∥
在直三棱柱ABC-A1B1C1中,BC⊥CA,点D1、F1分别是A1B1、A1C1的中点,若BC=CA=CC1,则异面直线BD1与AF1所成角的余弦值为( )
某个数学活动小组为了测量学校操场上国旗旗杆DC的高度,在旗杆的正西方向的点A测得旗杆顶端D的仰角为30度,沿点A向北偏东60度前进18米到达B点,测得旗杆顶端D的仰角为45度,经目测AB小于AC,则旗杆的高度为( )
()9米 ()16米 ()18米 ()9米或18米
如图是一个六棱柱的三视图,俯视图是一个周长为3的正六边形,该六棱柱的顶点都在同一个球面上,那么这个球的体积为( )
() () ()
7.等边三角形ABC的边长为4,M、N分别为AB、AC的中点,沿MN将△AMN折起,使得平面AMN与平面MNCB所成的二面角为30°,则四棱锥A—MNCB的体积为 ( )
() () () ()3
8.二面角的平面角为,在内,于B,AB=2,在内,于D,CD=3,BD=1, M是棱上的一个动点,则AM+CM的最小值为( )
() () () () 是的函数
9.设为两两不重合的平面,为两两不重合的直线.给出下列四个命题:①若,则;②若,则;③若,,则;④若,则,其中真命题的个数是 ( )
()1 ()2 ()3 ()4?
10.矩形ABCD中,AB=4,BC=2,E、F分别为AB、CD的中点,沿EF把BCFE折起后与ADFE垂直,P为矩形ADFE内一动点,P到平面BCFE的距离与它到点A的距离相等,设动点P的轨迹是曲线L,则曲线L把矩形ADFE分成的两部分的面积比为( )
()1:1 ()2:3 ()1:2 ()1:4
二、填空题
11.如图是一个几何体的三视图,俯视图是顶角为120度的
等腰三角形,则这个几何体的表面积为 .
用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥,
放在水平桌面上,被一阵风吹倒,如图,则它的最高点到桌面的距离为 .
在一个棱长为6厘米的密封正方体盒子中,放一个半径为1厘米的小球,任意摇动盒子,小球在盒子中不能达到的空间为G,则这个正方体盒子中的一点属于G的概率为 .
14.直角三角形ABC中,AD是斜边BC上的高,则AB是BD与BC的等比中项.
请利用类比推理给出:三棱锥P-ABC中,侧棱PA、PB、PC两两垂直,点P在底面上的射影为O,则 .
三、解答题
15.如图,四棱锥P-ABCD中,PA⊥底面ABCD,PC⊥AD.底面ABCD为梯形,AB∥DC,
AB⊥BC.PA=AB=BC,点E在棱PB上,且PE=2EB.
(1)求证:平面PAB⊥平面PCB;
(2)求证:PD∥平面EAC;
(3)求平面AEC和平面PBC所成锐二面角的余弦值.
16.在△ABC中,AB=CA=6,BC=8,点D、E、F分别是BC、AB、CA的中点,以三条中位线为折痕,折成一个三棱锥P-DEF,
求:(1)异面直线PD与EF所成的角;
(2)PD与底面DEF所成的角的正弦值;
(3)二面角P-DE-F的正弦值.
17.在长方体ABCD-A1B1C1D1中,AB=2,AA1=AD=1,点E,F,G分别是棱AA1、C1D1、BC的中点.
(1)在直线A1D1上是否存在点Q,使得EQ∥平面FB1G;
(2)求四面体EFGB1的体积;
(3)求平面EFB1与平面FB1G所成二面角的大小.
18.如图是三棱柱ABC-A1B1C1的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,D为AC的中点.
(1)求证:AB1∥平面BDC1;
(2)设AB1垂直于BC1,求二面角D-BC1-C的大小.
如图,平行四边形ABCD和矩形ACEF所在的平面互相垂直,AB=1,AD=2,
∠ADC=60°,AF=a(a>0).
(1)求证:AC⊥BF;
(2)若二面角F-BD-A的大小为60°,求a的值.
如图,AB为圆O的直径,点E,F在圆上,已知AB∥EF,AB=BC=4,AE=EF=BF=2,AD=2,直角梯形ABCD所在的平面与圆O所在的平面互相垂直.
(1)求证:平面CBE⊥平面DAE;
(2)求二面角F-CD-B的余弦值;
(3)在DB上是否存在一点G,使GF∥平面DAE 若不存在,请说明理由;若存在,请找出这一点,并证明之.
答案解析(专题四)
1.解析:选D.直线PC在平面PAB内的射影是∠BPA的平分线,设所求线面角为,则,故选D.
2. 解析:选.设圆柱的底面半径为,球的半径为,由于圆柱的轴截面为正方形,因此圆柱的母线长为,
所以,即,故选.
解析:选A. A对,在中有m与n不垂直的情况,在C中,还有m与n相交、异面的情况,在中,还有m与n相交、异面的情况,故选A.
4. 解析:选A.如图,建立空间直角坐标系,设BC=2,则
,
所以,
所以异面直线BD1与F1所成角的余弦值为,故选.
5. 解析:选C.如图,设,则,
,所以在中,
应用余弦定理得,
解这个方程得,
当时,,与已知矛盾,故舍去.当时符合题意,所以选C.
6. 解析:选.这是一个正六棱柱,上下两个底面的中心连线的中点就是球心,
因为六棱柱的高为,所以球心到底面的距离为.
因为底面正六边形的周长为3,所以底面正六边形的边长为,
即底面外接圆的半径为,由球的截面性质得球半径,
所以这个球的体积为,故选.
解析:选 .在平面图中,过A作AL⊥BC,交MN于K,交BC于L.则AK⊥MN,KL⊥MN.
∴∠AKL是面AMN与面MNCB所成的二面角的平面角,即有∠AKL=30°.
则四棱锥A—MNCB的高h==.=.
∴ =.故选 A.
8.解析:选C.如图,把平面展开到内成一个平面,连接AC,交于M,此时AM+CM=AC,过C作CN垂直于AB的延长线,垂足为N,则.故选C.
9. 解析:选.①也有相交的情况;②要保证相交,才有;③由面面平行的性质定理可知正确;④因,同样,从而,故④对.故选.?
10. 解析:选C.如图,过点P作PQ垂直于FE,则PQ垂直于平面BCFE,
所以PQ=PA,所以动点P的轨迹(即曲线L)为以A为焦点,以FE为准线的抛物线在矩形内的部分,在平面ADFE内,取AE中点为R,以R为原点,以RA为x轴,建立平面直角坐标系,则曲线L的方程为,曲线L与线段RA、AD围成的面积为,又矩形ADFE的面积为4,所以曲线L把矩形ADFE分成的两部分的面积比为1:2.故选C.
解析:根据三视图的知识,这个几何体是底面边长分别为的
等腰三角形,高为2的直三棱柱.它的侧面积是,其一个底面的面积为,所以这个三棱柱的表面积为.
答案:
12.解析:要抓住两点:1.半圆纸片的半径成了圆锥的母线,2.半圆弧长成了圆锥的底面周长.设圆锥的底面半径为,母线为,则,,
所以轴截面顶角的一半为,轴截面为正三角形,故圆锥的最高点离桌面的距离为厘米.
答案:厘米
解析:在正方体盒子中,不能到达的八个角的空间即为图一中的内切于正方体的小球不能到达的空间,其体积为.小球沿每条棱运动不能到达的空间(除去两端的两个角)的体积,即为高为4的一个正四棱柱的体积与其内接圆柱体积差的四分之一(如图二),
即,正方体有12条棱,所以在盒子中小球不能到达的空间G的体积为,又正方体盒子的体积为63=216,所这以个正方体盒子中的一点属于G的概率为.
答案:.
14.解析:连接CO,并延长交AB于D,连接PD,
则PD⊥PC,CD⊥AB,所以PD2=DO×DC,所以.即三角形PAB的面积是三角形AOB的面积与三角形ABC的面积的等比中项.
答案:三角形PAB的面积是三角形AOB的面积与三角形ABC的面积的等比中项.
15.解析: (1)∵PA⊥平面ABCD, ∴PA⊥BC.
又AB⊥BC,PAAB=A, ∴ BC⊥平面PAB.
又BC平面PCB,所以平面PAB⊥平面PCB.
(2)∵PA⊥底面ABCD,∴PA⊥AD,又PC⊥AD,PAPC=P,
∴AD⊥平面PAC,∴AC⊥AD.
在梯形ABCD中,由AB⊥BC,AB=BC,得∠BAC=45°,∴∠DCA=∠BAC=45°,
又AC⊥AD,故DAC为等腰直角三角形,
∴DC=AC=(AB)=2AB.
连结BD,交AC于点M,则.
连结EM,在BPD中,,
∴PD∥EM,又EM在平面EAC内,∴PD∥平面EAC.
(3)以A为坐标原点,AB,AP所在直线分别为y轴,z轴,建立如图所示空间直角坐标系.
设PA=AB=BC=a,则A(0,0,0),B(0,a,0),C(a,a,0),P(0,0,a),E.
设=(x,y,1)为平面AEC的一个法向量,
则⊥
∴,解得x=,y=,∴
设为平面PBC的一个法向量,则
又,解得,∴=(0,1,1).
,∴平面AEC和平面PBC所成的锐二面角的余弦值为.
16.解析:(1)取EF的中点N,连接DN、PN,
因为DF=DE,PF=PE,所以PN⊥EF,DN⊥EF,PNDN=N,
所以EF⊥平面PDN,EF⊥PD,所以异面直线PD与EF所成的角为90度.
(2)过点P作PO⊥DN,垂足为O,
由(1)知EF⊥平面PDN,所以平面PDN⊥平面DEF,
所以PO⊥平面DEF,DO是PD在平面DEF上的射影,
∠PDO就是直线PD与平面DEF所成的角.由题意得PN=DN=,PD=4,所以PO=,
所以.
(3)过O作OM⊥DE,垂足为M,连接PM,由(2)知PO⊥DE,又OM⊥DE,OMPO=O,所以DE⊥平面OPM,所以PM⊥DE,
∠PMO就是二面角P-DE-F的平面角.
因为sin∠PMO×sin∠PDM= sin∠PDO,在三角形PDE中,由余弦定理得PM=,
所以sin∠PDM=,所以sin∠PMO=,
所以二面角P-DE-F的正弦值为.
17.解析:如图以D为原点,以DA、DC、DD1所在直线分别为x,y,z轴,建立空间直角坐标系,
则E(1,0,),,,,
(1) 假设存在点Q,使得EQ∥平面FB1G,并设坐标为.
设面的法向量为,则
又,,
∴, 取,
因为∥平面,,
∴ ,∴ ,
故在的延长线上存在点Q,当时,有EQ∥面.
(2),则点E到平面FB1G的距离为
,
因为,
所以,
所以,所以所求的四面体的体积为;(3)设平面EFB1的法向量为,则,
所以,取,
根据两个法向量的方向,可知所求二面角的大小等于两个法向量的夹角的大小,
又因为,所以所求的二面角的大小为90度.
18.解析:
(1)由三视图画出直观图,如图,
这是一个正三棱柱,连接BC1和B1C,交点为O,则O为B1C的中点,连接OD,
因为D为中点,所以OD∥AB1,
又OD在平面BDC1内,AB1不在平面BDC1内,所以AB1∥平面BDC1.
(2)过D作DG⊥BC,垂足为G,连接GO,
因为侧面垂直于底面,所以DG⊥侧面BCC1B1,所以DO在侧面BCC1B1内的射影为GO,
因为AB1垂直于BC1,所以BC1⊥DO,又BC1⊥DG, DGDO=D,所以BC1⊥平面DOG,所以BC1⊥GO,所以∠DOG就是所求的二面角的平面角.
取BC中点F,连接AF,OF,则有OF⊥BC,AF⊥BC,
在直角三角形BOG中,OF⊥BG,
所以,,
故在直角三角形DGO中,DG=OG,∠DOG=450,即所求的二面角的大小为45度.
解析: (1)如图,
在ABC中,∵AB=1,BC=2,∠ABC=60°,
∴由余弦定理得=,
∴,∴∠BAC=90°,即AC⊥AB.
又在矩形ACEF中,AC⊥AF,且AFAB=A,
∴AC⊥平面ABF,又∵BF平面ABF,∴AC⊥BF.
(2)∵平面ACEF⊥平面ABCD,平面ACEF平面ABCD=AC,FA⊥AC,∴FA⊥平面ABCD,
过点A作AG⊥BD于点G,连结FG,则FG⊥BD.
∴∠AGF即是二面角F-BD-A的平面角,∴∠AGF=60°.
在ABD中,由余弦定理得
由
在RtAGF中,∵∠AGF=60°,∴AF=AG·tan∠AGF=
20.解析:(1)如图,
连结BE,因为四边形ABCD是直角梯形,所以AD⊥AB,
又平面ABCD⊥平面ABFE,
所以AD⊥平面ABFE,所以AD⊥BE.
因为AB为圆O的直径,所以AE⊥BE,又AEAD=A,所以BE⊥平面DAE.
又BE平面CBE,所以平面CBE⊥平面DAE.
(2)因为AE=EF=BF=2,连结OE,OF,则OEF是边长为2的等边三角形,以O为原点,OB所在直线为y轴,垂直于OB的直线分别为x轴,z轴,建立如图坐标系,
则有A(0,-2,0),B(0,2,0),C(0,2,4),D(0,-2,2),F(,1,0),
易得平面ABCD的一个法向量为,设平面CDF的一个法向量为因为,
由
所以
结合图形知平面CDF与平面ABCD所成角的余弦值为
存在,点G是BD的中点.
证明:连结OG,GF,则OG∥AD,又因为OG平面DAE,所以OG∥平面DAE,因为AB∥EF,AO=AB=2,EF=2,所以四边形AOFE是平行四边形,所以OF∥AE,又OF平面DAE,所以OF∥平面DAE,又OGOF=O,所以平面OGF∥平面DAE,所以GF∥平面DAE.
同课章节目录
