2013年高考数学(课标版)原创预测题(理科):专题二 三角函数、三角变换、解三角形、平面向量、复数
文档属性
| 名称 | 2013年高考数学(课标版)原创预测题(理科):专题二 三角函数、三角变换、解三角形、平面向量、复数 |  | |
| 格式 | zip | ||
| 文件大小 | 172.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-22 15:40:55 | ||
图片预览
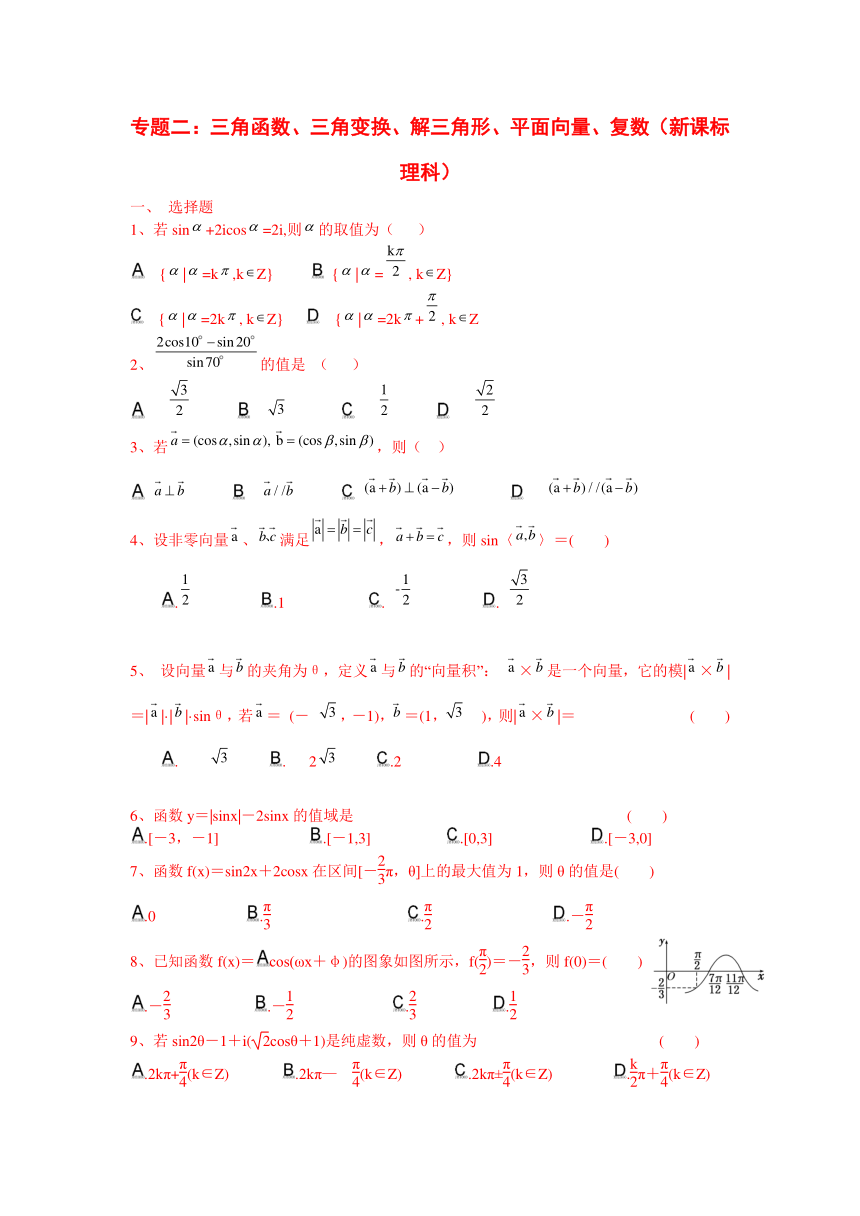


文档简介
专题二:三角函数、三角变换、解三角形、平面向量、复数(新课标理科)
一、 选择题
1、若sin+2icos=2i,则的取值为( )
{|=k,kZ} {|=, kZ}
{|=2k, kZ} {|=2k+, kZ
2、的值是 ( )
3、若,则( )
4、设非零向量、满足,,则sin〈〉=( )
. .1 . .
5、 设向量与的夹角为θ,定义与的“向量积”: ×是一个向量,它的模|×|=||·||·sinθ,若= (- ,-1),=(1, ),则|×|= ( )
. . 2 .2 .4
6、函数y=|sinx|-2sinx的值域是 ( )
.[-3,-1] .[-1,3] .[0,3] .[-3,0]
7、函数f(x)=sin2x+2cosx在区间[-π,θ]上的最大值为1,则θ的值是( )
.0 . . .-
8、已知函数f(x)=cos(ωx+φ)的图象如图所示,f()=-,则f(0)=( )
.- .- . .
9、若sin2θ-1+i(cosθ+1)是纯虚数,则θ的值为 ( )
.2kπ+(k∈Z) .2kπ— (k∈Z) .2kπ±(k∈Z) .π+(k∈Z)
10、某人在点测得某塔在南偏西80°,塔顶仰角为45°,此人沿南偏东40°
方向前进10米到,测得塔顶的仰角为30°,则塔高为 ( )
.15米 .5米 .10米 .12米
二、 填空题
11、 已知sincos=,且,则cos-sin=________________
12、设△的内角,,所对的边长分别为a,b,c且acos-bcos=c.则的值为 .
13.已知函数f(x)=2sin(ωx+φ)的图象如下图所示,则f()= .
14、 已知向量=(2,-1),=(x,-2),=(3,y),若∥,(+)⊥(-),M(x,y),N(y,x),则向量的模为 .
三、解答题
15、 已知 3cos+2sin2= 求(1)tan的值 ,(2)3cos2+4sin2的值
16、已知函数f(x)=3sin(x-),x∈R.
(1)画出函数f(x)在长度为一个周期的闭区间上的简图;
(2)将函数y=sinx的图象作怎样的变换可得到f(x)的图象?
17、 在中,若bsin+csin=2bccoscos,试判断三角形的形状
18、已知函数f(x)=sin2ωx+sinωxsin(ωx+)+2cos2ωx,x∈R(ω>0),在y轴右侧的第一个最高点的横坐标为.
(1)求ω;(2)若将函数f(x)的图象向右平移个单位后,再将得到的图象上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)的最大值及单调递减区间.
19、在△中,设内角,,的对边分别为,向量=(cos,sin),向量=(-sin,cos),
若||=2.
(1)求角的大小;
(2)若b=4,且c=a,求△的面积.
20、已知向量=(sin,1),=(cos,cos2).
(1)若=1,求cos(-x)的值;
(2)记f(x)=,在△中,角,,的对边分别是a,b,c,且满足(2a-c)cos=bcos,
求函数f()的取值范围.
三角函数、三角变换、解三角形、平面向量、复数(新理)
试题答案
1解析:选,由复数相等的条件得:sin=0,cos=1,所以的终边落在x轴的正半轴上,故选;
2解析:选,原式====
3解析:选, =(cos+cos)( cos-cos)+(sin+sin)( sin-sin)
=cos+sin-cos=0选项正确
4 解析:选,∵,∴=又∴
即2||||cos〈,〉=-.∴cos〈〉= - sin=
5解析:选, cos= ==-
6 解析:选,当0≤sinx≤1时,y=sinx-2sinx=-sinx,此时y∈[-1,0];当-1≤sinx<0时,
y=-sinx-2sinx=-3sinx,这时y∈(0,3],求其并集得y∈[-1,3].
7 解析:选,因为f(x)=sin2x+2cosx=-cos2x+2cosx+1=-(cosx-1)2+2,又其在区间[-,θ]上的最大值为1,结合选项可知θ只能取-.,故选
8解析: 选,由题意可知,此函数的周期T=2(π-π)=,故=,∴ω=3,f(x)=cos(3x+φ).
f ()=cos(+φ)=sinφ=-.又由题图可知f()=cos(3×+φ)=cos(φ-π)
=(cosφ+sinφ)=0,∴f(0)=cosφ=.
9解析:选,由题意,得 ∴θ=2kπ+,k∈Z.
10解析:选,如图,设塔高为h,在Rt△O中,∠O=45°,
则O=O=h.在Rt△O中,∠O=30°,则O=h,
在△O中,∠O=120°,=10,
由余弦定理得:O2=O2+2-2O·cos∠O,即(h)2=h2+102-2h×10×cos120°,
∴h2-5h-50=0,解得h=10,或h=-5(舍).
二 填空题
11解析:cos-sin=—=—=—=
答案:
12解析:由acos-bcos=c及正弦定理可得sincos-sincos=sin,即sincos-sincos
=sin(+),即5(sincos-sincos)=3(sincos+sincos),即sincos=4sincos,因此
tan=4tan,所以=4.
答案:4
13解析:由图象知,函数的周期为×T=π,∴T=. ∵f()=0,
∴f()=f(+)=f(+)=-f()=0. 答案:0
14解析:∵∥,∴x=4,∴b=(4,-2),∴+=(6,-3),-=(1,-2-y).∵(+)⊥(-),
∴(+)·(-)=0,即6-3(-2-y)=0,∴y=-4,故向量=(-8,8),
| |=8. 答案:8
三解答题
15解析:(1)由已知条件得4cos+4sincos+sin=0,(2cos+sin)=0,
所以2cos=-sin tan=-2
(2) 3cos2+4sin2===-5
16解析:(1)列表取值:
x
0
f(x)
0
3
0
-3
0
描出五个关键点并用光滑曲线连接,得到一个周期的简图.
(2)先把y=sinx的图象向右平移个单位,然后纵坐标不变,把所有点的横坐标扩大为原来的2倍,再横坐标不变,把所有点的纵坐标扩大为原来的3倍,得到f(x)的图象.
17解析:由=2R,及条件得4Rsinsin+4Rsinsin=8Rsinsincoscos
又sinsin≠0 sinsin=coscos,即cos(+)=0,又0°<+<180°+=90°=90°
故是直角三角形.
18解析:(1)f(x)=sin2ωx+cos2ωx+=sin(2ωx+)+.
令2ωx+=,将x=代入可得:ω=1.
(2)由(1)得f(x)=sin(2x+)+.经过题设的变化得到的函数g(x)=sin(x-)+.
当x=4kπ+π,k∈Z时,函数取得最大值. 令2kπ+≤x-≤2kπ+π,
即[4kπ+,4kπ+π],k∈Z为函数的单调递减区间.
19解析: (1) ∵||2=(cos+-sin)2+(sin+cos)2=4+2(cos-sin)=4+4cos(+),
∴4+4cos(+)=4,∴cos(+)=0,∵∈(0,π),∴+=,∴=.
(2)由余弦定理知:a2=b2+c2-2bccos, 即a2=(4)2+(a) 2-2×4×acos,
解得a=4,∴c=8, ∴S△=bcsin=×4×8×=16.
20解析:(1)∵=1,即sincos+cos2=1,即sin+cos+=1,
∴sin (+)=.cos(-x)=cos(x-)=-cos(x+)
=-[1-2sin2(+)]=2·()2-1=-.
(2)∵(2a-c)cos=bcos,由正弦定理得(2sin-sin)cos=sincos.
∴2sincos-cossin=sincos,∴2sincos=sin(+),
∵++=π,
∴sin(+)=sin,且sin≠0,∴cos=,=,
∴0<<.∴<+<,<sin(+)<1.
又∵f(x)==sin(+)+,∴f()=sin(+)+.
故函数f()的取值范围是(1,).
一、 选择题
1、若sin+2icos=2i,则的取值为( )
{|=k,kZ} {|=, kZ}
{|=2k, kZ} {|=2k+, kZ
2、的值是 ( )
3、若,则( )
4、设非零向量、满足,,则sin〈〉=( )
. .1 . .
5、 设向量与的夹角为θ,定义与的“向量积”: ×是一个向量,它的模|×|=||·||·sinθ,若= (- ,-1),=(1, ),则|×|= ( )
. . 2 .2 .4
6、函数y=|sinx|-2sinx的值域是 ( )
.[-3,-1] .[-1,3] .[0,3] .[-3,0]
7、函数f(x)=sin2x+2cosx在区间[-π,θ]上的最大值为1,则θ的值是( )
.0 . . .-
8、已知函数f(x)=cos(ωx+φ)的图象如图所示,f()=-,则f(0)=( )
.- .- . .
9、若sin2θ-1+i(cosθ+1)是纯虚数,则θ的值为 ( )
.2kπ+(k∈Z) .2kπ— (k∈Z) .2kπ±(k∈Z) .π+(k∈Z)
10、某人在点测得某塔在南偏西80°,塔顶仰角为45°,此人沿南偏东40°
方向前进10米到,测得塔顶的仰角为30°,则塔高为 ( )
.15米 .5米 .10米 .12米
二、 填空题
11、 已知sincos=,且,则cos-sin=________________
12、设△的内角,,所对的边长分别为a,b,c且acos-bcos=c.则的值为 .
13.已知函数f(x)=2sin(ωx+φ)的图象如下图所示,则f()= .
14、 已知向量=(2,-1),=(x,-2),=(3,y),若∥,(+)⊥(-),M(x,y),N(y,x),则向量的模为 .
三、解答题
15、 已知 3cos+2sin2= 求(1)tan的值 ,(2)3cos2+4sin2的值
16、已知函数f(x)=3sin(x-),x∈R.
(1)画出函数f(x)在长度为一个周期的闭区间上的简图;
(2)将函数y=sinx的图象作怎样的变换可得到f(x)的图象?
17、 在中,若bsin+csin=2bccoscos,试判断三角形的形状
18、已知函数f(x)=sin2ωx+sinωxsin(ωx+)+2cos2ωx,x∈R(ω>0),在y轴右侧的第一个最高点的横坐标为.
(1)求ω;(2)若将函数f(x)的图象向右平移个单位后,再将得到的图象上各点横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)的最大值及单调递减区间.
19、在△中,设内角,,的对边分别为,向量=(cos,sin),向量=(-sin,cos),
若||=2.
(1)求角的大小;
(2)若b=4,且c=a,求△的面积.
20、已知向量=(sin,1),=(cos,cos2).
(1)若=1,求cos(-x)的值;
(2)记f(x)=,在△中,角,,的对边分别是a,b,c,且满足(2a-c)cos=bcos,
求函数f()的取值范围.
三角函数、三角变换、解三角形、平面向量、复数(新理)
试题答案
1解析:选,由复数相等的条件得:sin=0,cos=1,所以的终边落在x轴的正半轴上,故选;
2解析:选,原式====
3解析:选, =(cos+cos)( cos-cos)+(sin+sin)( sin-sin)
=cos+sin-cos=0选项正确
4 解析:选,∵,∴=又∴
即2||||cos〈,〉=-.∴cos〈〉= - sin=
5解析:选, cos= ==-
6 解析:选,当0≤sinx≤1时,y=sinx-2sinx=-sinx,此时y∈[-1,0];当-1≤sinx<0时,
y=-sinx-2sinx=-3sinx,这时y∈(0,3],求其并集得y∈[-1,3].
7 解析:选,因为f(x)=sin2x+2cosx=-cos2x+2cosx+1=-(cosx-1)2+2,又其在区间[-,θ]上的最大值为1,结合选项可知θ只能取-.,故选
8解析: 选,由题意可知,此函数的周期T=2(π-π)=,故=,∴ω=3,f(x)=cos(3x+φ).
f ()=cos(+φ)=sinφ=-.又由题图可知f()=cos(3×+φ)=cos(φ-π)
=(cosφ+sinφ)=0,∴f(0)=cosφ=.
9解析:选,由题意,得 ∴θ=2kπ+,k∈Z.
10解析:选,如图,设塔高为h,在Rt△O中,∠O=45°,
则O=O=h.在Rt△O中,∠O=30°,则O=h,
在△O中,∠O=120°,=10,
由余弦定理得:O2=O2+2-2O·cos∠O,即(h)2=h2+102-2h×10×cos120°,
∴h2-5h-50=0,解得h=10,或h=-5(舍).
二 填空题
11解析:cos-sin=—=—=—=
答案:
12解析:由acos-bcos=c及正弦定理可得sincos-sincos=sin,即sincos-sincos
=sin(+),即5(sincos-sincos)=3(sincos+sincos),即sincos=4sincos,因此
tan=4tan,所以=4.
答案:4
13解析:由图象知,函数的周期为×T=π,∴T=. ∵f()=0,
∴f()=f(+)=f(+)=-f()=0. 答案:0
14解析:∵∥,∴x=4,∴b=(4,-2),∴+=(6,-3),-=(1,-2-y).∵(+)⊥(-),
∴(+)·(-)=0,即6-3(-2-y)=0,∴y=-4,故向量=(-8,8),
| |=8. 答案:8
三解答题
15解析:(1)由已知条件得4cos+4sincos+sin=0,(2cos+sin)=0,
所以2cos=-sin tan=-2
(2) 3cos2+4sin2===-5
16解析:(1)列表取值:
x
0
f(x)
0
3
0
-3
0
描出五个关键点并用光滑曲线连接,得到一个周期的简图.
(2)先把y=sinx的图象向右平移个单位,然后纵坐标不变,把所有点的横坐标扩大为原来的2倍,再横坐标不变,把所有点的纵坐标扩大为原来的3倍,得到f(x)的图象.
17解析:由=2R,及条件得4Rsinsin+4Rsinsin=8Rsinsincoscos
又sinsin≠0 sinsin=coscos,即cos(+)=0,又0°<+<180°+=90°=90°
故是直角三角形.
18解析:(1)f(x)=sin2ωx+cos2ωx+=sin(2ωx+)+.
令2ωx+=,将x=代入可得:ω=1.
(2)由(1)得f(x)=sin(2x+)+.经过题设的变化得到的函数g(x)=sin(x-)+.
当x=4kπ+π,k∈Z时,函数取得最大值. 令2kπ+≤x-≤2kπ+π,
即[4kπ+,4kπ+π],k∈Z为函数的单调递减区间.
19解析: (1) ∵||2=(cos+-sin)2+(sin+cos)2=4+2(cos-sin)=4+4cos(+),
∴4+4cos(+)=4,∴cos(+)=0,∵∈(0,π),∴+=,∴=.
(2)由余弦定理知:a2=b2+c2-2bccos, 即a2=(4)2+(a) 2-2×4×acos,
解得a=4,∴c=8, ∴S△=bcsin=×4×8×=16.
20解析:(1)∵=1,即sincos+cos2=1,即sin+cos+=1,
∴sin (+)=.cos(-x)=cos(x-)=-cos(x+)
=-[1-2sin2(+)]=2·()2-1=-.
(2)∵(2a-c)cos=bcos,由正弦定理得(2sin-sin)cos=sincos.
∴2sincos-cossin=sincos,∴2sincos=sin(+),
∵++=π,
∴sin(+)=sin,且sin≠0,∴cos=,=,
∴0<<.∴<+<,<sin(+)<1.
又∵f(x)==sin(+)+,∴f()=sin(+)+.
故函数f()的取值范围是(1,).
同课章节目录
