冀教版数学七年级下册 9.3 三角形的角平分线、中线和高 课件(共20张PPT)
文档属性
| 名称 | 冀教版数学七年级下册 9.3 三角形的角平分线、中线和高 课件(共20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 808.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-15 17:03:43 | ||
图片预览




文档简介
(共20张PPT)
9.3 三角形的角平分线、中线和高
教学目标:
经历折纸、画图理解三角形的角平分线、中线、和高.
会画已知三角形的角平分线、中线和高
让学生了解“叠合”法是几何中对“相等关系”进行验证试验、探究的一种重要方法
本节重点:三角形三种重要线段的性质.
本节难点:三角形三条角平分线、三条中线、三条高分别交于一点
复分线定义
学生在半透明的纸上画任意角用折纸的方法找出它的角平分线
角平分线是一条射线
复习导入
是指从一个角的顶点引出的一条射线, 把这个角分成两个相等的角。
∴∠AOC=∠BOC= ∠AOB
O
B
A
C
角平分线:
∵OC是∠AOB的角平分线
设计意图 利用其区别三角形的角平分线,为得出三角形角平分线定义做铺垫。
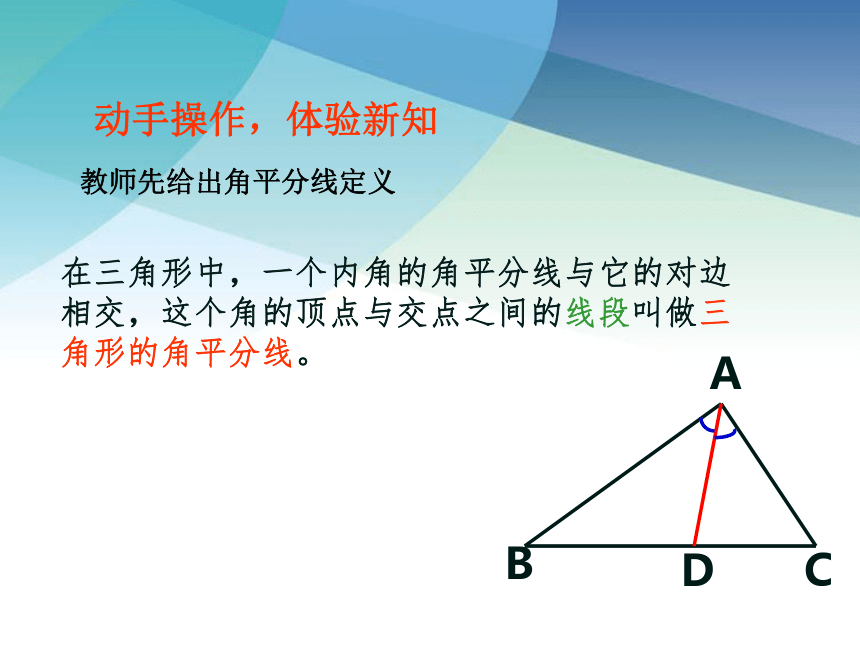
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
C
A
D
B
教师先给出角平分线定义
动手操作,体验新知
A
B
C
D
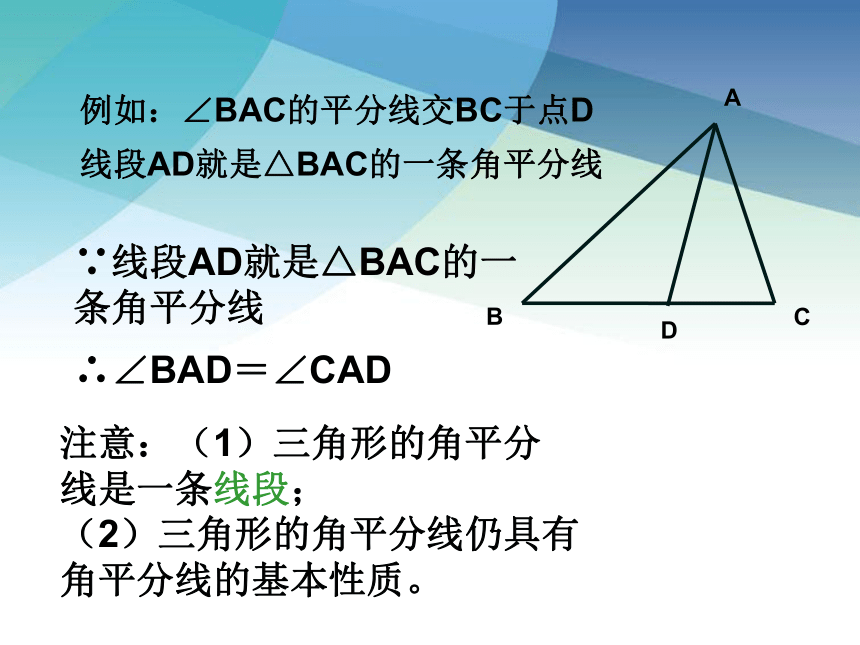
例如:∠BAC的平分线交BC于点D
线段AD就是△BAC的一条角平分线
注意:(1)三角形的角平分线是一条线段;
(2)三角形的角平分线仍具有角平分线的基本性质。
∵线段AD就是△BAC的一条角平分线
∴∠BAD=∠CAD
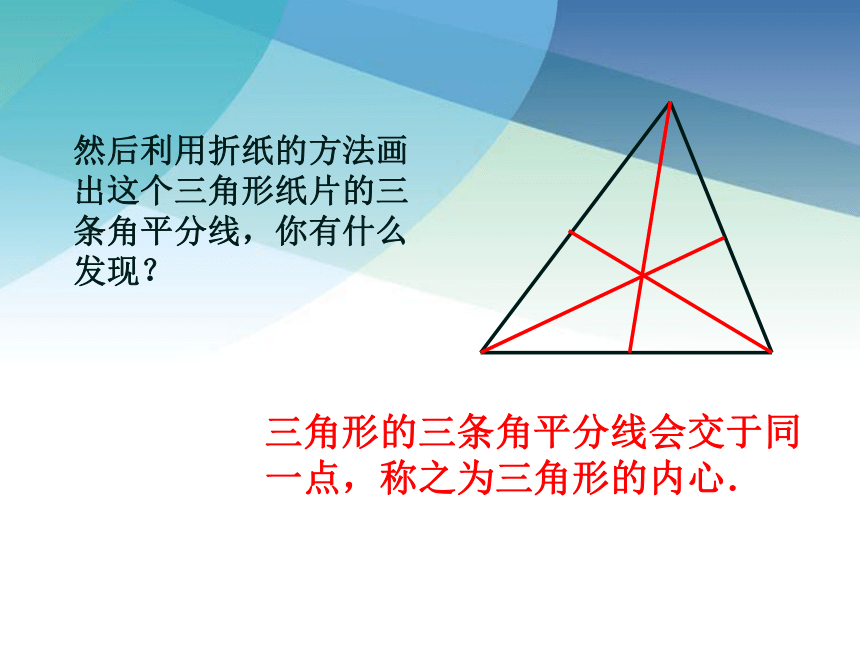
三角形的三条角平分线会交于同一点,称之为三角形的内心.
然后利用折纸的方法画出这个三角形纸片的三条角平分线,你有什么发现?
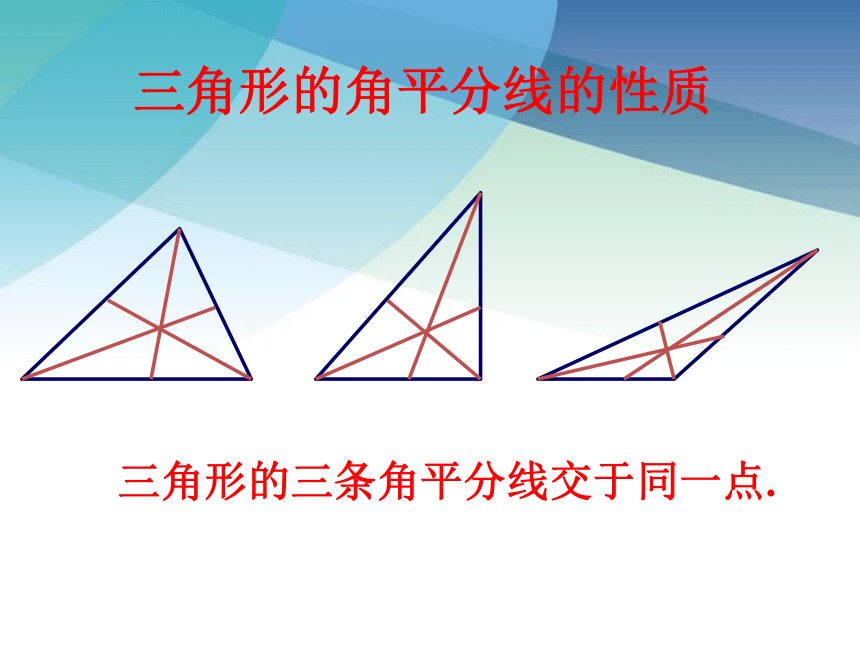
三角形的角平分线的性质
三角形的三条角平分线交于同一点.
定义: 在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线
拿出准备好的任意三角形纸片,用折纸的方法找到一边中点画出这边中线,然后画出三角形的三条中线。观察三线位置,用锐角三角形纸、钝角三角形纸片、直角三角形纸片都试一下,概括其性质。
三角形的中线
A
B
C
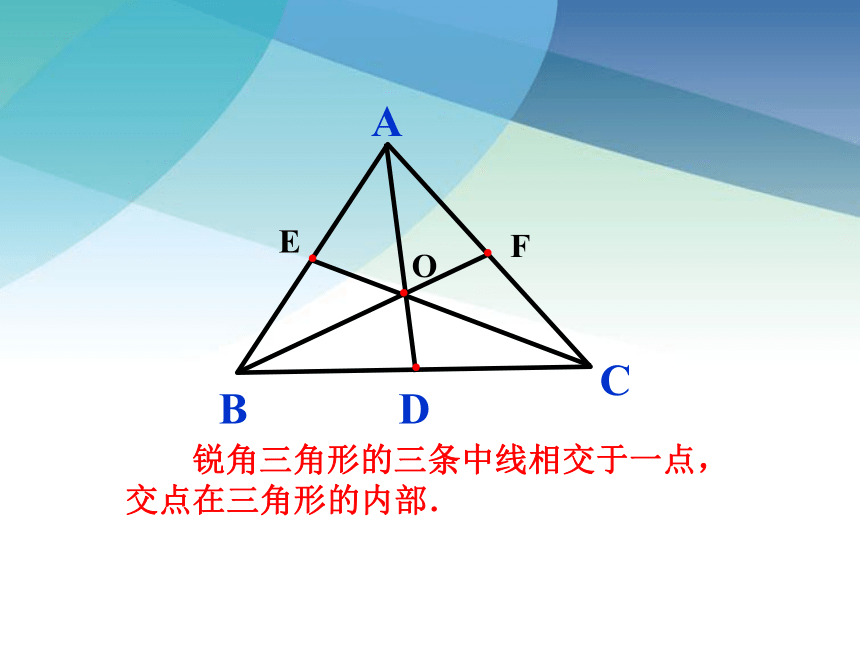
锐角三角形的三条中线相交于一点,交点在三角形的内部.
●
●
●
●
D
E
F
O
D
E
F
P
O
I
直角三角形的三条中线相交于一点,交点在三角形的内部.
●
●
●
┓
G
H
I
M
N
P
钝角三角形的三条中线相交于一点,交点在三角形的内部.
●
●
●
三角形的高
你还记得 “过直线外一点画已知直线的垂线” 吗?
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
┓
三角形的高
从三角形的一个顶点向它的对边所在的直线作
垂线,顶点和垂足之间的线段叫做三角形的高线(简称“高”).
1. 直角三角形两直角边是三角形两条高
2. 钝角三角形有两高在三角形外
注意:
A
B
C
D
A
B
C
D
E
F
三角形的三条高所在的直线交于一点.
O
A
B
C
D
E
F
O
锐角三角形 直角三角形 钝角三角形
角平分线
中线
高线
请根据自己的实践总结出交点的三种位置
锐角三角形 直角三角形 钝角三角形
高线 三角形的内部
直角的顶点 三角形外部
中线 三角形的内部
角平分线 三角形的内部
设计意图:学生通过自己动手实践,观察、交流得出结论,在自我活动和相互交流中获得知识,体验乐趣。
拿出提前准备好的三角形纸片,画出这个三角形的三条中线,在它们的交点出钻一个小孔,通过小空系一条线将三角形硬纸板吊起.从三角形硬纸板所处的状态来看,有什么现象?换一处试试?这种现象说明了什么?
1. 小明在做题时,不小心用墨水把图的一部分给涂抹了.你能根据已知条件“AD是三角形ABC的角平分线”帮助小明把这个三角形被遮住的部分画出来吗?试着画一画1
A
B
C
D
E
2:如图,D是BC中点S△ ABD与S△ ADC有什么关系
9.3 三角形的角平分线、中线和高
教学目标:
经历折纸、画图理解三角形的角平分线、中线、和高.
会画已知三角形的角平分线、中线和高
让学生了解“叠合”法是几何中对“相等关系”进行验证试验、探究的一种重要方法
本节重点:三角形三种重要线段的性质.
本节难点:三角形三条角平分线、三条中线、三条高分别交于一点
复分线定义
学生在半透明的纸上画任意角用折纸的方法找出它的角平分线
角平分线是一条射线
复习导入
是指从一个角的顶点引出的一条射线, 把这个角分成两个相等的角。
∴∠AOC=∠BOC= ∠AOB
O
B
A
C
角平分线:
∵OC是∠AOB的角平分线
设计意图 利用其区别三角形的角平分线,为得出三角形角平分线定义做铺垫。
在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
C
A
D
B
教师先给出角平分线定义
动手操作,体验新知
A
B
C
D
例如:∠BAC的平分线交BC于点D
线段AD就是△BAC的一条角平分线
注意:(1)三角形的角平分线是一条线段;
(2)三角形的角平分线仍具有角平分线的基本性质。
∵线段AD就是△BAC的一条角平分线
∴∠BAD=∠CAD
三角形的三条角平分线会交于同一点,称之为三角形的内心.
然后利用折纸的方法画出这个三角形纸片的三条角平分线,你有什么发现?
三角形的角平分线的性质
三角形的三条角平分线交于同一点.
定义: 在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形的中线
拿出准备好的任意三角形纸片,用折纸的方法找到一边中点画出这边中线,然后画出三角形的三条中线。观察三线位置,用锐角三角形纸、钝角三角形纸片、直角三角形纸片都试一下,概括其性质。
三角形的中线
A
B
C
锐角三角形的三条中线相交于一点,交点在三角形的内部.
●
●
●
●
D
E
F
O
D
E
F
P
O
I
直角三角形的三条中线相交于一点,交点在三角形的内部.
●
●
●
┓
G
H
I
M
N
P
钝角三角形的三条中线相交于一点,交点在三角形的内部.
●
●
●
三角形的高
你还记得 “过直线外一点画已知直线的垂线” 吗?
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
┓
三角形的高
从三角形的一个顶点向它的对边所在的直线作
垂线,顶点和垂足之间的线段叫做三角形的高线(简称“高”).
1. 直角三角形两直角边是三角形两条高
2. 钝角三角形有两高在三角形外
注意:
A
B
C
D
A
B
C
D
E
F
三角形的三条高所在的直线交于一点.
O
A
B
C
D
E
F
O
锐角三角形 直角三角形 钝角三角形
角平分线
中线
高线
请根据自己的实践总结出交点的三种位置
锐角三角形 直角三角形 钝角三角形
高线 三角形的内部
直角的顶点 三角形外部
中线 三角形的内部
角平分线 三角形的内部
设计意图:学生通过自己动手实践,观察、交流得出结论,在自我活动和相互交流中获得知识,体验乐趣。
拿出提前准备好的三角形纸片,画出这个三角形的三条中线,在它们的交点出钻一个小孔,通过小空系一条线将三角形硬纸板吊起.从三角形硬纸板所处的状态来看,有什么现象?换一处试试?这种现象说明了什么?
1. 小明在做题时,不小心用墨水把图的一部分给涂抹了.你能根据已知条件“AD是三角形ABC的角平分线”帮助小明把这个三角形被遮住的部分画出来吗?试着画一画1
A
B
C
D
E
2:如图,D是BC中点S△ ABD与S△ ADC有什么关系
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
