北师大版数学七年级下册 第五章 生活中的轴对称 专题四 模型拓展 课件(共15张)
文档属性
| 名称 | 北师大版数学七年级下册 第五章 生活中的轴对称 专题四 模型拓展 课件(共15张) |  | |
| 格式 | pptx | ||
| 文件大小 | 418.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-15 18:13:11 | ||
图片预览





文档简介
(共15张PPT)
单元复习课
专题四 模型拓展
模型一:“一线两点”型(一动点+两定点)
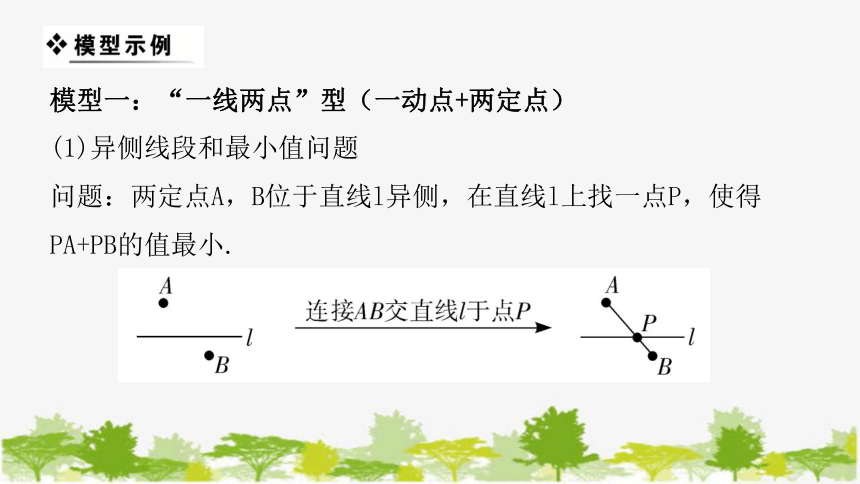
(1)异侧线段和最小值问题
问题:两定点A,B位于直线l异侧,在直线l上找一点P,使得PA+PB的值最小.
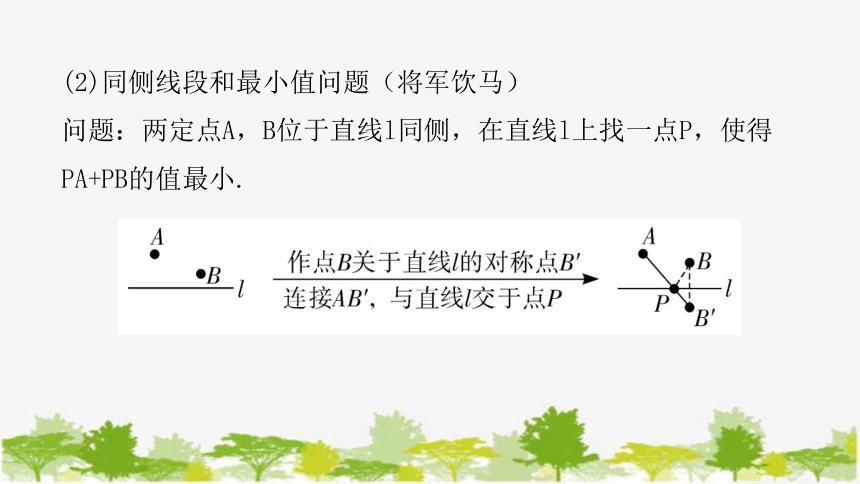
(2)同侧线段和最小值问题(将军饮马)
问题:两定点A,B位于直线l同侧,在直线l上找一点P,使得PA+PB的值最小.
(3)同侧线段差最大值问题
问题:两定点A,B位于直线l同侧,在直线l上找一点P,使得PA-PB的值最大.
(4)异侧线段差最大值问题
问题:两定点A,B位于直线l异侧,在直线l上找一点P,使得PA-PB的值最大.
1. 已知点P在∠MON内.
(1)如图D5-4-1①,点P关于射线OM的对称点是点G,点P关于射线ON的对称点是点H,连接OG,OH,OP.
①若∠MON=50°,则∠GOH= ;
②若OP=5,连接GH,请说明
当∠MON为多少度时,GH=10;
100°
(2)如图D5-4-1②,若∠MON=60°,A,B分别是射线OM,ON上的任意一点,当△PAB的周长最小时,求∠APB的度数.
解:(1) ②当∠MON=90°时,GH=10. 理由如下:
因为OP=5,所以OG=OH=5.
当∠MON=90°时,∠GOH=180°,
此时点G,O,H在同一直线上,
所以GH=OG+OH=10.
(2)如答图D5-4-1,分别作点P关于OM,ON的对称点P′,P″,连接OP,OP′,OP″,P′P″,P′P″交OM,ON于点A,B,连接PA,PB,则AP=AP′,BP=BP″,此时△PAB的周长的最小值为AP+AB+BP=AP′+AB+BP″=P′P″.
由轴对称的性质,得OP′=OP″=OP,∠P′OA=∠POA,∠P″OB=∠POB,所以∠P′OP″=2∠MON=2×60°=120°.
所以∠OP′P″=∠OP″P′=(180°-120°)÷2=30°.
所以∠OPA=∠OP′A=30°.同理可得∠OPB=∠OP″B=30°.
所以∠APB=∠OPA+∠OPB=30°+30°=60°.
模型二:“一点两线”型(两动点+一定点)
(1)周长最小值问题
问题:点P是∠AOB内部一定点,在OA上找一点M,在OB上找一点N,使得△PMN的周长最小.
(2)两条线段之和最小值问题
问题:点P是∠AOB内部一定点,在OA上找一点M,OB上找一点N,使得PN+MN的值最小.
2. 某班级在探究“将军饮马问题”时抽象出数学模型:
直线l同旁有两个定点A,B,在直线l上存在点P,使得PA+PB的值最小.解法:如图D5-4-2①,作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.
请利用上述模型解决下列问题:
(1)如图D5-4-2②,△ABC中,∠C=90°,E是AB的中点,P是BC边上的一动点,作出点P,使得PA+PE的值最小;
(2)如图D5-4-2③,∠AOB=30°,M,N分别为OA,OB上一动点,若OP=5,求△PMN的周长的最小值.
解:(1)如答图D5-4-2,作点A关于直线BC
的对称点A1,连接A1E,交BC于点P,点P即
为所求.
(2)作点P关于直线OA的对称点F,作点P关于直线OB的对称点G,连接FG,分别交OA,OB于点M,N,如答图D5-4-3.
所以PM=FM,PN=GN.
所以PM+MN+PN=FM+MN+GN=FG.
此时△PMN的周长的最小值等于FG的长.
由轴对称的性质,得∠FOA=∠AOP,
∠POB=∠GOB,OP=OF,OP=OG.
因为∠AOP+∠POB=∠AOB=30°,OP=5,
所以∠FOG=∠FOA+∠AOP+∠POB+∠GOB=60°,OF=OG=5.
所以△FOG是边长为5的等边三角形.
所以FG=5.
所以△PMN的周长的最小值为5.
谢 谢
单元复习课
专题四 模型拓展
模型一:“一线两点”型(一动点+两定点)
(1)异侧线段和最小值问题
问题:两定点A,B位于直线l异侧,在直线l上找一点P,使得PA+PB的值最小.
(2)同侧线段和最小值问题(将军饮马)
问题:两定点A,B位于直线l同侧,在直线l上找一点P,使得PA+PB的值最小.
(3)同侧线段差最大值问题
问题:两定点A,B位于直线l同侧,在直线l上找一点P,使得PA-PB的值最大.
(4)异侧线段差最大值问题
问题:两定点A,B位于直线l异侧,在直线l上找一点P,使得PA-PB的值最大.
1. 已知点P在∠MON内.
(1)如图D5-4-1①,点P关于射线OM的对称点是点G,点P关于射线ON的对称点是点H,连接OG,OH,OP.
①若∠MON=50°,则∠GOH= ;
②若OP=5,连接GH,请说明
当∠MON为多少度时,GH=10;
100°
(2)如图D5-4-1②,若∠MON=60°,A,B分别是射线OM,ON上的任意一点,当△PAB的周长最小时,求∠APB的度数.
解:(1) ②当∠MON=90°时,GH=10. 理由如下:
因为OP=5,所以OG=OH=5.
当∠MON=90°时,∠GOH=180°,
此时点G,O,H在同一直线上,
所以GH=OG+OH=10.
(2)如答图D5-4-1,分别作点P关于OM,ON的对称点P′,P″,连接OP,OP′,OP″,P′P″,P′P″交OM,ON于点A,B,连接PA,PB,则AP=AP′,BP=BP″,此时△PAB的周长的最小值为AP+AB+BP=AP′+AB+BP″=P′P″.
由轴对称的性质,得OP′=OP″=OP,∠P′OA=∠POA,∠P″OB=∠POB,所以∠P′OP″=2∠MON=2×60°=120°.
所以∠OP′P″=∠OP″P′=(180°-120°)÷2=30°.
所以∠OPA=∠OP′A=30°.同理可得∠OPB=∠OP″B=30°.
所以∠APB=∠OPA+∠OPB=30°+30°=60°.
模型二:“一点两线”型(两动点+一定点)
(1)周长最小值问题
问题:点P是∠AOB内部一定点,在OA上找一点M,在OB上找一点N,使得△PMN的周长最小.
(2)两条线段之和最小值问题
问题:点P是∠AOB内部一定点,在OA上找一点M,OB上找一点N,使得PN+MN的值最小.
2. 某班级在探究“将军饮马问题”时抽象出数学模型:
直线l同旁有两个定点A,B,在直线l上存在点P,使得PA+PB的值最小.解法:如图D5-4-2①,作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点即为P,且PA+PB的最小值为A′B.
请利用上述模型解决下列问题:
(1)如图D5-4-2②,△ABC中,∠C=90°,E是AB的中点,P是BC边上的一动点,作出点P,使得PA+PE的值最小;
(2)如图D5-4-2③,∠AOB=30°,M,N分别为OA,OB上一动点,若OP=5,求△PMN的周长的最小值.
解:(1)如答图D5-4-2,作点A关于直线BC
的对称点A1,连接A1E,交BC于点P,点P即
为所求.
(2)作点P关于直线OA的对称点F,作点P关于直线OB的对称点G,连接FG,分别交OA,OB于点M,N,如答图D5-4-3.
所以PM=FM,PN=GN.
所以PM+MN+PN=FM+MN+GN=FG.
此时△PMN的周长的最小值等于FG的长.
由轴对称的性质,得∠FOA=∠AOP,
∠POB=∠GOB,OP=OF,OP=OG.
因为∠AOP+∠POB=∠AOB=30°,OP=5,
所以∠FOG=∠FOA+∠AOP+∠POB+∠GOB=60°,OF=OG=5.
所以△FOG是边长为5的等边三角形.
所以FG=5.
所以△PMN的周长的最小值为5.
谢 谢
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
