人教版七年级下册 5.2.2 平行线的判定 课件(共19页)
文档属性
| 名称 | 人教版七年级下册 5.2.2 平行线的判定 课件(共19页) |

|
|
| 格式 | zip | ||
| 文件大小 | 500.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-15 19:39:55 | ||
图片预览





文档简介
(共19张PPT)
【义务教育教科书人教版七年级下册】
5.2.2 平行线的判定
回顾旧知
1.什么叫同位角?内错角?怎样的两个角是同旁内角?
2.判定两条直线平行的方法
同位角:在被截直线同一方向,在截线同侧;
内错角:在被截直线之间,在截线两侧;
同旁内角:在被截直线之间,在截线同侧(旁).
(1)平行线的定义;
(2)平行公理及推论。
同位角(F型)
内错角(Z型或N型)
同旁内角(U型)
归纳总结
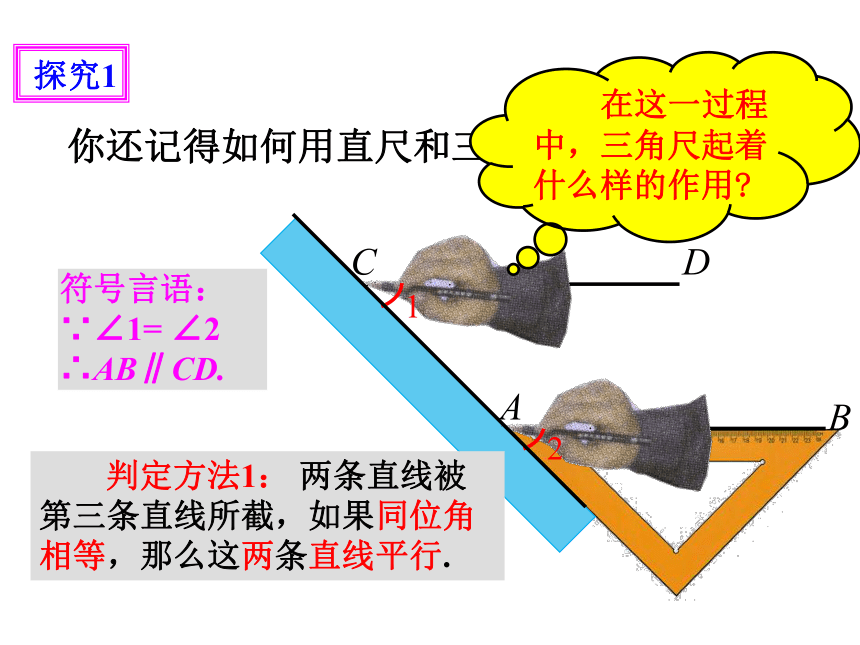
探究1
你还记得如何用直尺和三角尺画平行线吗?
A
B
C
D
在这一过程中,三角尺起着什么样的作用
判定方法1: 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
符号言语:
∵∠1= ∠2
∴AB∥CD.
1
2
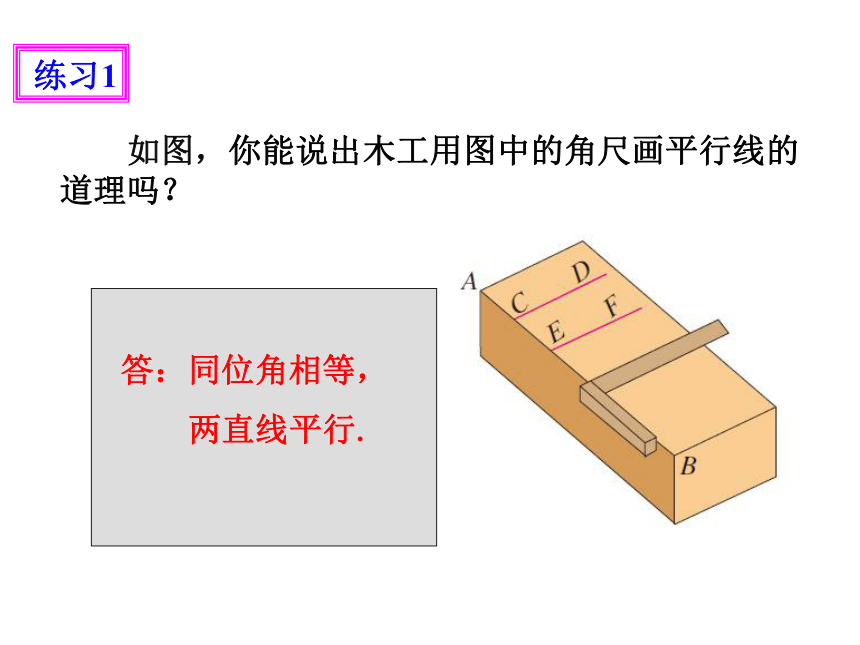
答:同位角相等,
两直线平行.
如图,你能说出木工用图中的角尺画平行线的道理吗?
练习1
探究2
判定方法2: 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
符号言语:
∵∠2= ∠3
∴a∥b.
如果两条直线被第三条直线所截,那么能否利用内错角来判定两条直线平行呢
证明:
∵∠2= ∠3
∠1= ∠3
∴∠1=∠2
∴a∥b.
如果∠2= ∠3,能得出a∥b吗
答:
∵∠1= ∠2
∴AB∥CD;
∵∠DCE=∠D
∴AD∥BC.
练习2
如图,由∠1=∠2 可判断哪两条直线平行?由 ∠DCE=∠D ,可判断哪两条直线平行?
B
探究3
判定方法3: 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
符号言语:
∵∠2+∠4=1800
∴a∥b.
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢
证明:
∵∠1+∠4=1800
∠2+∠4=1800 ∴∠1=∠2
∴a∥b.
如果∠2+ ∠4=1800,能得出a∥b吗
归纳
判定方法1:同位角相等,两直线平行.
判定方法2:内错角相等,两直线平行.
判定方法3:同旁内角互补,两直线平行.
平行线的判定
答: AB∥CD .根据内错角相等,两直线平行.
1.如果∠1=∠2,能判定哪两条直线平行?为什么?
练习3
答: DE∥FB. 根据同位角相等,两直线平行.
2.如果∠1=∠3,能判定哪两条直线平行?为什么?
练习3
答: AD∥CB.根据同旁内角互补,两直线平行.
3.如果∠A+∠ABC=180 ,能判定哪两条直线平行?为什么?
练习3
例:在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?
应用提高
已知条件:
b⊥a, c⊥a
答:这两直线平行.
理由如下:
∵ b⊥a,∴ ∠1= 90°.
同理∠2= 90°.
∴ ∠1=∠2.
∵ ∠1和∠2是同位角,
∴ b∥c(同位角相等,两直线平行)
1
2
你还能用其他方法说明理由吗?
今天我们学习了哪些知识?
1.本节课,你学习了哪些平行线的判定方法?
2.结合实际,能用自己的语言说一说解决与平行线的判定有关的问题的思路吗?
体验收获
达标测评
1. 如图所示, 如果∠D=∠EFC,那么( )
A. AD∥BC
B. EF∥BC
C. AB∥DC
D. AD∥EF
D
达标测评
2. 如图所示,下列条件中,能判断AB∥CD的是( )
A.∠BAD+∠ABC=1800
B.∠1=∠2;
C.∠3=∠4
D.∠BAC=∠ACD
D
达标测评
答: AB∥CD .
理由如下:
∵ AC平分∠BAD,
∴ ∠1=∠3 .
∵∠1=∠2,
∴ ∠2=∠3 .
∵ ∠2和∠3是内错角,
∴ AB∥CD(内错角相等,两直线平行).
3. 已知:如图,四边形ABCD中,AC平分∠BAD,∠1=∠2,AB与CD平行吗?为什么?
布置作业
教材16页习题5.2第6、12题.
【义务教育教科书人教版七年级下册】
5.2.2 平行线的判定
回顾旧知
1.什么叫同位角?内错角?怎样的两个角是同旁内角?
2.判定两条直线平行的方法
同位角:在被截直线同一方向,在截线同侧;
内错角:在被截直线之间,在截线两侧;
同旁内角:在被截直线之间,在截线同侧(旁).
(1)平行线的定义;
(2)平行公理及推论。
同位角(F型)
内错角(Z型或N型)
同旁内角(U型)
归纳总结
探究1
你还记得如何用直尺和三角尺画平行线吗?
A
B
C
D
在这一过程中,三角尺起着什么样的作用
判定方法1: 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
符号言语:
∵∠1= ∠2
∴AB∥CD.
1
2
答:同位角相等,
两直线平行.
如图,你能说出木工用图中的角尺画平行线的道理吗?
练习1
探究2
判定方法2: 两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
符号言语:
∵∠2= ∠3
∴a∥b.
如果两条直线被第三条直线所截,那么能否利用内错角来判定两条直线平行呢
证明:
∵∠2= ∠3
∠1= ∠3
∴∠1=∠2
∴a∥b.
如果∠2= ∠3,能得出a∥b吗
答:
∵∠1= ∠2
∴AB∥CD;
∵∠DCE=∠D
∴AD∥BC.
练习2
如图,由∠1=∠2 可判断哪两条直线平行?由 ∠DCE=∠D ,可判断哪两条直线平行?
B
探究3
判定方法3: 两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
符号言语:
∵∠2+∠4=1800
∴a∥b.
如果两条直线被第三条直线所截,那么能否利用同旁内角来判定两条直线平行呢
证明:
∵∠1+∠4=1800
∠2+∠4=1800 ∴∠1=∠2
∴a∥b.
如果∠2+ ∠4=1800,能得出a∥b吗
归纳
判定方法1:同位角相等,两直线平行.
判定方法2:内错角相等,两直线平行.
判定方法3:同旁内角互补,两直线平行.
平行线的判定
答: AB∥CD .根据内错角相等,两直线平行.
1.如果∠1=∠2,能判定哪两条直线平行?为什么?
练习3
答: DE∥FB. 根据同位角相等,两直线平行.
2.如果∠1=∠3,能判定哪两条直线平行?为什么?
练习3
答: AD∥CB.根据同旁内角互补,两直线平行.
3.如果∠A+∠ABC=180 ,能判定哪两条直线平行?为什么?
练习3
例:在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?
应用提高
已知条件:
b⊥a, c⊥a
答:这两直线平行.
理由如下:
∵ b⊥a,∴ ∠1= 90°.
同理∠2= 90°.
∴ ∠1=∠2.
∵ ∠1和∠2是同位角,
∴ b∥c(同位角相等,两直线平行)
1
2
你还能用其他方法说明理由吗?
今天我们学习了哪些知识?
1.本节课,你学习了哪些平行线的判定方法?
2.结合实际,能用自己的语言说一说解决与平行线的判定有关的问题的思路吗?
体验收获
达标测评
1. 如图所示, 如果∠D=∠EFC,那么( )
A. AD∥BC
B. EF∥BC
C. AB∥DC
D. AD∥EF
D
达标测评
2. 如图所示,下列条件中,能判断AB∥CD的是( )
A.∠BAD+∠ABC=1800
B.∠1=∠2;
C.∠3=∠4
D.∠BAC=∠ACD
D
达标测评
答: AB∥CD .
理由如下:
∵ AC平分∠BAD,
∴ ∠1=∠3 .
∵∠1=∠2,
∴ ∠2=∠3 .
∵ ∠2和∠3是内错角,
∴ AB∥CD(内错角相等,两直线平行).
3. 已知:如图,四边形ABCD中,AC平分∠BAD,∠1=∠2,AB与CD平行吗?为什么?
布置作业
教材16页习题5.2第6、12题.
