五年级下学期数学第四单元《长方体(二)》练习四及单元复习课件(共59张PPT)
文档属性
| 名称 | 五年级下学期数学第四单元《长方体(二)》练习四及单元复习课件(共59张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-15 06:38:44 | ||
图片预览










文档简介
(共59张PPT)
练习四及单元复习题库
第四单元 长方体(二)复习
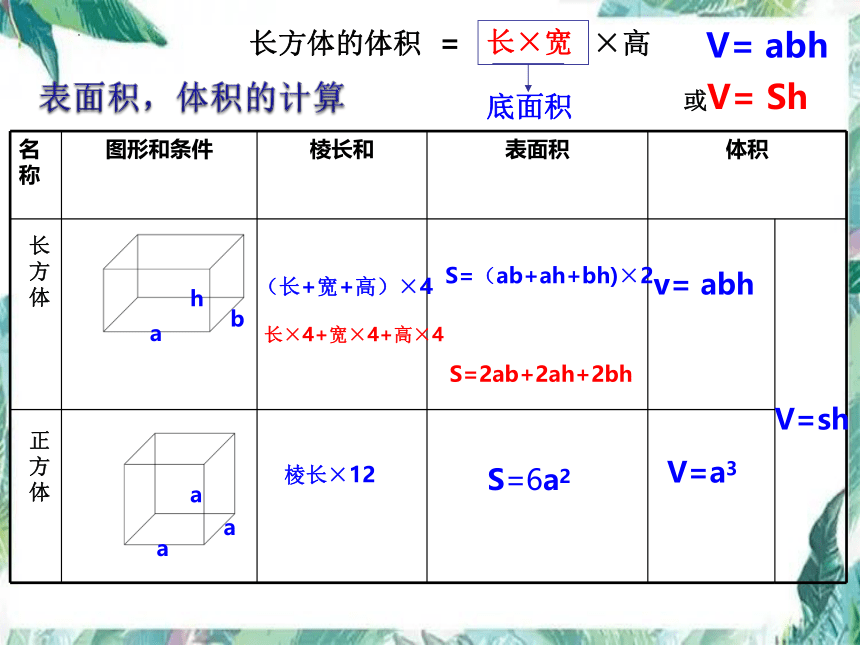
表面积,体积的计算
名称 图形和条件 棱长和 表面积 体积
棱长×12
(长+宽+高)×4
S=(ab+ah+bh)×2
v= abh
V=a3
V=sh
a
a
a
a
b
h
长方体
正方体
S=6a2
长×4+宽×4+高×4
S=2ab+2ah+2bh
长方体的体积 =
V= abh
长×宽 ×高
底面积
长×宽
或V= Sh
因为小正方体的体积都一样大,左边的图形有12个小正方体,右边的图形有16个小正方体,座椅右边的图形所占的空间更大。
它们所占的空间不一样大。
1.用棱长为1cm的小正方体拼成下列两个图形,
它们所占的空间一样大吗?为什么?
教材P48T1优
cm3
dm3
cm3
m3
教材P48T2优
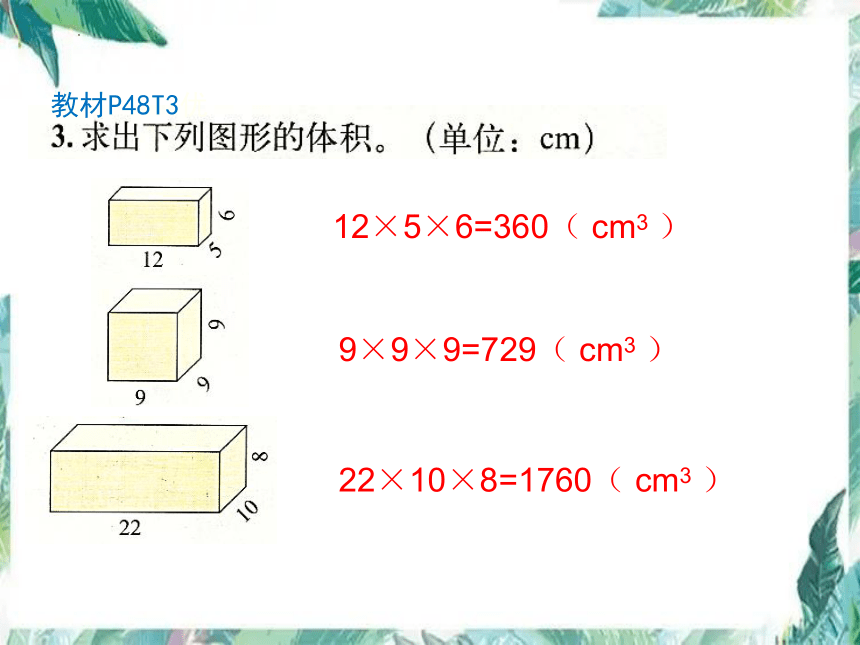
12×5×6=360( cm3 )
9×9×9=729( cm3 )
22×10×8=1760( cm3 )
教材P48T3优
12×4×3=144(cm3)
答:这个长方体的体积是144cm3。
教材P48T4优
0.35m3=( )dm3
350
5300dm3=( )m3
5.3
19.6L=( )mL
19600
2.04dm3=( )cm3
2800cm3=( )dm3
1325mL=( )L
2040
2.8
1.325
5.
教材P48T5优
6.下面两组数中,每一组都有一个数与其他数不同,
请划去这个数。
教材P48T6优6
6×6×6=216(cm2)
6×6×6=216(cm3)
答:它的表面积是216cm2,它的体积是216cm3。
7.一个棱长为6cm的正方体药盒,它的表面积和体积
分别是多少?
教材P48T7优
200L=200000(cm )
50×50=2500(cm2)
200000÷2500=80(cm)
答:水箱的高是80厘米。
8.一个长方体水箱的容积是200L,这个水箱的底面是一个边长为50cm的正方形,水箱的高是多少厘米?
教材P49T8优
6cm=0.06m
45×28×0.06=75.6(m3)
答:需要75.6立方米的沙土。
教材P49T9优
75.6÷1.5≈51(次)
答:至少需要运51次。
教材P49T9优
15×26×7=2730(cm3)
15×26×40=15600(cm3)
2730×2+15600=21060(cm3)
答:这个旅行包的容积大约是21060cm3。
10.如图,一种旅行包的A,B,C三部分用拉链连接,拆卸方便。这种旅行包可以近似地看成是由右边的三个图形组成的,这个旅行包的容积大约是多少?(单位:cm)
教材P49T10优
5×2×2+12×2×2+12×5=128(dm2)
答:最少需要128dm2的铁皮,这个水槽最多可以盛
120L水。
5×12×2=120(dm )=120(L)
11.做一个如右图的无盖长方体铁皮水槽最少需要多大面积的铁皮?这个水槽最多可以盛多少升水?(单位:dm)
教材P49T11优
50cm=5dm
40cm=4dm
30cm=3dm
5×4×3=60(L)
答:这个油箱能装60升汽油。
12.某汽车油箱的长、宽、高如右图所示。(单位:cm)
(1)这个油箱能装多少升汽油?
教材P49T12优
12.某汽车油箱的长、宽、高如右图所示。(单位:cm)
(2)如果每升汽油可行驶10km,这箱油最多可以供
这辆汽车行驶多少千米?
60×10=600(km)
答:这箱油最多可以供这辆
汽车行驶600千米。
教材P49T12优
不可以。
8个
能,27个。
(答案不唯一)
教材P49T13优
二、基础练习
1.判断对错。
×
(1)一个木头箱子的体积就是它的容积。 ( )
(2)长方体是特殊的正方体。 ( )
(3)棱长是6分米的正方体它的体积和表面积相等。 ( )
(4)用4个棱长1厘米的小正方体可以拼成一个大正方体。 ( )
×
×
×
五年级下册数学课件 长方体和正方体复习课【PPT完美】
单元复习题(1)
二、基础练习
1.判断对错。
√
(5)体积单位和容积单位的进率都是1000。 ( )
(6)把一个正方体铸造成一个长方体,虽然它的形状变了,但是它的体积没有变。 ( )
(7)一块石头完全浸到盛有水的容器里,溢出的水的体积就是石头的体积。 ( )
√
√
五年级下册数学课件 长方体和正方体复习课【PPT完美】
五年级下册数学课件 长方体和正方体复习课【PPT完美】
二、基础练习
面积
长度
6
体积
(1)计量一个长方体的棱长总和用( )单位,计量它的表面积用的是( )单位,计量它的体积用( )单位。
(2)一个正方体的棱长是1厘米,它的表面积是( )平方厘米,它的体积是( )立方厘米。
(3)一辆汽车的油箱能装油72( ),数学书的体积是320( )。
(4)一个长方体长3厘米、宽2厘米、高1厘米,那它的棱长总和是( )。
1
cm3
24厘米
2.填空。
L
五年级下册数学课件 长方体和正方体复习课【PPT完美】
五年级下册数学课件 长方体和正方体复习课【PPT完美】
二、基础练习
3.按要求计算。(单位:cm)
6
5
4
4
4
4
表面积:
体积:
表面积:
体积:
棱长总和:
2×(6 × 5+5 × 4+6 × 4)=148(cm2)
6 × 5 × 4=120(cm3)
6×(4 × 4)=96(cm2)
4 × 4 × 4=64(cm3)
4 × 12=48(cm)
五年级下册数学课件 长方体和正方体复习课【PPT完美】
五年级下册数学课件 长方体和正方体复习课【PPT完美】
二、基础练习
4.一个长方体和一个正方体的棱长总和相等。已知长方体的长、宽、高分别是9 dm、6 dm、3 dm,那么正方体的棱长是多少分米?它们的体积相等吗?
(9+6+3)×4=72(dm) 72÷12=6(dm )
长方体体积:9×6×3=162(dm3)
正方体体积:6×6×6=216(dm3)
不相等
三、易错练习
1.单位换算。
1020
360
3400
1.02 dm3=( )cm3 3.4 m3=( )dm3 ( )mL=0.36 L
2090 cm3=( )L 6.5 m3=( )m3( )dm3
2.09
6
500
五年级下册数学课件 长方体和正方体复习课【PPT完美】
五年级下册数学课件 长方体和正方体复习课【PPT完美】
三、易错练习
C
2.我会选。
(1)一瓶花露水的包装盒上印有“净含量100毫升”的字样,这个“100毫升”是指( )。
A.包装盒的体积 B.包装盒的容积 C.瓶中花露水的体积
(2)一个正方体的棱长扩大到原来的2倍,表面积扩大到原来的( )倍,体积扩大到原来的( )倍。
A.2 B.4 C.8
B
C
五年级下册数学课件 长方体和正方体复习课【PPT完美】
五年级下册数学课件 长方体和正方体复习课【PPT完美】
三、易错练习
A
2.我会选。
(3)一个长方体的棱长之和是180厘米,相交于一个顶点的三条棱的长度和是( )。
A.45厘米 B.30厘米 C.90厘米
(4)从一个长方体中挖掉一个角(如图),它的表面积( )。
A.比原来小 B.比原来大 C.与原来一样大
C
五年级下册数学课件 长方体和正方体复习课【PPT完美】
五年级下册数学课件 长方体和正方体复习课【PPT完美】
三、易错练习
2.我会选。
(5)下列图形不能折成正方体的是( )。
A
B
C
C
五年级下册数学课件 长方体和正方体复习课【PPT完美】
五年级下册数学课件 长方体和正方体复习课【PPT完美】
三、易错练习
3.解决问题。
1.2×1×0.5=0.6(立方米) 0.6立方米=600升 600×0.8=480(千克)
(1)一个油箱里面长1.2米,宽1米,高0.5米,给油箱盛满汽油。如果1升汽油重0.8千克。这个油箱共盛汽油多少千克?
(2)一个游泳池长25米,宽18米,深2米,要给它的四周和底面贴上瓷砖如果每平方米用瓷砖16块,这个游泳池共需瓷砖多少块?
25×18+25×2×2+18×2×2=450+100+72=622 (平方米)
16×622=9952(块)
五年级下册数学课件 长方体和正方体复习课【PPT完美】
五年级下册数学课件 长方体和正方体复习课【PPT完美】
三、易错练习
4.一个长方体的无盖的铁皮水槽,长4 m,宽45 cm,高是1.2 m。
(1)这个铁皮水槽占地面积多大?
(2)需要多少平方米的铁皮?
(3)它的体积是多少?
45 cm=0.45 m 4×0.45=1.8(m2)
4×0.45+(4×1.2+0.45×1.2)×2=12.48(m2)
4×0.45×1.2=2.16(m3)
四、拓展练习
1.一个长方体的底面是一个周长为20 cm的长方形,高为2 cm,如果长和宽的厘米数都是质数,那么这个长方体的体积是多少?
20÷2=10=3+7 3×7×2=42(cm3)
四、拓展练习
正方体的棱长是84÷3÷4=7(厘米)
原长方体的体积是7×7×(7-3)=196(立方厘米)
2.一个长方体,如果高增加3 cm,那么就变成一个正方体。这时表面积比原来增加84 cm2。原来长方体的体积是多少立方厘米?
(1)两个完全一样的长方体拼成一个大长方体,表面积不变。( )
×
判断 。
×
×
×
√
(2)长方体的6个面是完全相同的长方形。 ( )
(3)有六个面的物体不是长方体就是正方体。( )
(5)用八个完全相同的小正方体,可以拼成一个大正方体。( )
(4)棱长为2厘米的正方体,它的棱长之和与它的表面积相等。( )
单元复习题(2)
(1)下列物体中,形状不是长方体的是( )。
A.火柴盒 B.红砖 C.足球 D.木箱
(2)长方体有( )条棱,( )个面,( )个顶点。
A. 4 B.6 C. 8 D. 12
(3)把一个棱长3分米的正方体切成两个相等的长方体,增加的两个面的总面积是( )平方分米。
A.18 B. 9 C. 36 D.以上答案都不对
选择。
C
D
B
C
A
无盖正方体玻璃鱼缸,没有上面,一共有5个面。
做一个棱长为3分米无盖正方体玻璃鱼缸至少需要多大面积的玻璃?
3 ×3 ×5
=9 ×5
=45(平方分米)
答:至少需要45平方分米的玻璃。
下面哪些图形是正方体的展开图?是的画√,错的画×,再利用附页1中的图2试一试。
×
√
√
√
√
×
小兰的房间长4m,宽3m,高3m。除去门窗5m ,房间的墙壁和房顶都贴上墙纸,这个房间至少需要多大面积的墙纸?
4 ×3+(3 ×3+4×3)×2-5
=12+42-5
=49(m )
答:至少需要49平方米的墙纸。
用3个棱长都是1厘米的正方体,拼成一个长方体,这个拼成的长方体表面积是多少?
1 ×3 ×4+1 ×1 ×2
=12+2
=14(平方厘米)
答:这个拼成的长方体表面积是14平方厘米。
用一根36厘米长的铁丝围成一个正方体(接头处不计),这个正方体的表面积是多少平方厘米
(36÷12)×(36÷12)×6
=3×3×6
=54(平方厘米)
答:这个正方体的表面积是54平方厘米。
3个棱长都是30厘米的正方体堆放在墙角处(如下图),露在外面的面积是多少?
30 × 30 × 7
=900×7
= 6300(平方厘米)
答:露在外面的面积是6300 平方厘米。
(1)相交于一个顶点的三条棱的长度分别叫作长方体的( )、( )、( )。
(2)求长方体的棱长总和方法:( )×4+( )×4+( )×4=棱长总和; 也就是( + + )×4=总棱长。
(3)一个长方体的长是10dm,宽是6 dm,高是4 dm,它的棱长总和是( )dm。
(4)一个长方体的棱长总和是80cm,其中长是10cm,宽是5cm,高是( )cm。
填空。
长
宽
高
长
宽
高
长
宽
高
80
5
一个火柴盒长4厘米,宽2厘米,高1.5厘米,做一个完整的火柴盒,至少需要多少纸板?(纸盒厚度不计)
火 柴
外壳 (4×2+2×1.5)×2
= 11×2
=22 ( c㎡ )
火柴盒外壳有上、下、左、右四个面
火柴盒内匣有前、后、左、右、下五个面(缺上面)。
完整的盒子=外+里
22+26=48(c㎡)
答:至少需要48平方厘米的材料。
里盒 (4×1.5+2×1.5)×2+4×2
=9×2+8
=26 (c㎡)
一根绳子长10m,现要捆扎一种礼盒,(如下图)如果接头处要用掉绳子25cm,这根绳子最多可以捆扎几个这样的礼盒?(单位:cm)
10 ×2+8 ×4+15 ×2+25
= 20+32+30+25
= 107(cm)
10m=1000cm
1000÷107=9(个)……37(cm)
答:最多可以捆扎9个这样的礼盒。
40
25
40
淘淘要把一个如下图所示的空包装箱的各个面都贴上彩纸,至少需要多少平方厘米彩纸?(单位:厘米)
40×25×4+40×40×2
=4000+3200
=7200(平方厘米)
答:至少需要7200平方厘米彩纸。
6个棱长都是20厘米的纸箱堆放在墙角处,如下图,露出多少个面?露在外面的面积是多少平方厘米?
露出13个面
20 ×20 ×13
=400 ×13
=5200(平方厘米)
答:露在外面的面积是5200平方厘米.
将一个由5个棱长是10厘米的正方体排成的长方体拆开,如下图,5个正方体的表面积是多少?与长方体的表面积相等吗?与同伴交流。
10 ×10×6×5
=600 ×5
=3000(平方厘米)
答:5个正方体的表面积是3000平方厘米。
与长方形的表面积不相等,拆开后比原来的长方体增加了8个面。
课堂小结
通过本节课的复习你有哪些收获?
名称
内容
项目
长方体
正方体
6个长方形面(最多有2个面是正方形),相对面的面积相等。
12条,每4条长度相等(也可能有8条相等)。每相交于一个顶点的棱分别是长、宽、高。
8个
6个都是完全相同的正方形面
12条,长度都相等。
8个
S表=(a · b+b · h+a · h) ×2
长方体的表面积=(长×宽+宽×高+长×高)×2
长方体的体积=长×宽×高
V= a · b · h
V= S底 · h (其中S底 = a · b
特征
面
棱
顶点
公式
表面积和体积
一、梳理知识
长方体和正方体的特征及公式(一览表)
S表=a2 ×6
正方体的表面积=棱长×棱长×6
V= a · a · a 即a3
长方体的体积=棱长×棱长×棱长
或a2 )
长方体和正方体的特征
形体 相同点 不同点 联系
面 棱 顶点 面的 形状 面的 面积 棱长 正方体是一种特殊的长方体
长方体 6个 12条 8个 6个面都是长方形,有时相对的两个面是正方形 相对的两个面的面积相等 相对的棱的长度相等
正方体 6个面都是正方形 6个面面积都相等 12条棱都相等
长方体和正方体的表面积
S长方体=2ab+2ah+2bh
=2(ab+ah+bh)
S正方体=6a2
长方体和正方体6个面的总面积,叫做它的表面积
a
b
h
a
a
a
长方体和正方体的体积(容积)
体积:物体所占空间的大小。
容积:所能容纳物体空间的大小。
V长方体=abh
V正方体=a3
V=sh
a
b
h
a
a
a
体积(容积)的单位
立方米(m3)
立方分米(dm3)----升(l)
立方厘米(cm3)----毫升(ml)
体积(容积)相邻单位之间的进率是 1000。
把四盒牛奶拼在一起,哪种最省包装材料?
4cm
7cm
10cm
减少的面积:
7×10×6=420(cm2)
减少的面积:
10×7×4+4×10×4=440(cm2)
减少的面积最大
所以最省材料
设计包装盒
★★(1)把一根长30厘米的长方体木料锯成3段(如图),表面积比原来增加了20平方厘米,这根木料原来的体积是多少立方厘米
★★★(2)一个底面是正方形的长方体,把它的侧面展开后得到一个边长是8厘米的正方形。求这个长方体的体积是多少?
选做:
分析
分析
★★(1)把一根长30厘米的长方体木料锯成3段(如图),表面积比原来增加了20平方厘米,这根木料原来的体积是多少立方厘米
选做:
20÷4=5(平方厘米)
30×5=150(平方厘米)
答:这根木材原来的体积是150平方厘米。
1.
小明家准备做一个鱼缸,长1.2米,宽5分米,高6分米。至少需要多少平方米的玻璃材料?它最多可以装水多少升?
2.
装修小明的卧室地面用了360块长50厘米,宽10厘米,厚3厘米的木质地板。请你算算,小明的卧室有多大?至少要用木材多少立方米?
C.深化题
1.2×0.5+0.5×0.6×2+0.6×1.2×2
=0.6+0.3×2+0.72×2
=0.6+0.6+1.44
=2.64 (平方米)
12×5×6
=60×6
=360 (升)
答:至少需要2.64平方米的玻璃材料。最多可以装水360升。
0.5×0.1×360=18 (平方米)
18 ×0.03=0.54 (立方米)
答:小明的卧室有18平方米,至少要用木材0.54立方米。
50厘米=0.5米 10厘米=0.1米 3厘米=0.03米
红岩
红岩
57毫升
R
蓝黑墨水
蓝黑墨水
重庆红岩墨水有限责公司
红岩
6. 5
6
4.3
如图,做一个墨水盒至少需要多少平方厘米的硬纸?这个纸盒的体积是多少?(图上单位:厘米)
1.
棱长6分米的正方体,它的体积和表面积各是多少?
2.
B.基础题
(6.5×4.3+4.3×6+6×6.5)×2
体积:
表面积:
=(27.95+25.8+39)×2
= 92.75×2
= 185.5 (平方厘米)
6.5×4.3×6
=27.95×6
=167.7 (立方厘米)
答:做这个墨水盒至少需要185.5平方厘米的硬纸,这个纸盒的体积是167.7立方厘米。
答:这个正方体的体积是216立方分米,表面积是216平方分米。
62 ×6 =216 (平方分米)
表面积:
63 =216 (立方分米)
体积:
★★★(2)一个底面是正方形的长方体,把它的侧面展开后得到一个边长是8厘米的正方形。求这个长方体的体积是多少?
选做:
8
8
8
2
2
8÷4=2(厘米)
2×2×8=32(立方厘米)
答:这个长方体的体积是108立方厘米。
这个魔方玩具是由一些棱长3厘米的小正方体合成,请迅速计算出该魔方的体积和表面积。
32 × 9 × 6 = 486 (平方厘米)
32 × (9 × 6)
或(3 × 3)2 × 6
33 × 9 ×3= 729 (立方厘米)
33 × (9 ×3)
或(3 × 3)3
D.拓展题
练习四及单元复习题库
第四单元 长方体(二)复习
表面积,体积的计算
名称 图形和条件 棱长和 表面积 体积
棱长×12
(长+宽+高)×4
S=(ab+ah+bh)×2
v= abh
V=a3
V=sh
a
a
a
a
b
h
长方体
正方体
S=6a2
长×4+宽×4+高×4
S=2ab+2ah+2bh
长方体的体积 =
V= abh
长×宽 ×高
底面积
长×宽
或V= Sh
因为小正方体的体积都一样大,左边的图形有12个小正方体,右边的图形有16个小正方体,座椅右边的图形所占的空间更大。
它们所占的空间不一样大。
1.用棱长为1cm的小正方体拼成下列两个图形,
它们所占的空间一样大吗?为什么?
教材P48T1优
cm3
dm3
cm3
m3
教材P48T2优
12×5×6=360( cm3 )
9×9×9=729( cm3 )
22×10×8=1760( cm3 )
教材P48T3优
12×4×3=144(cm3)
答:这个长方体的体积是144cm3。
教材P48T4优
0.35m3=( )dm3
350
5300dm3=( )m3
5.3
19.6L=( )mL
19600
2.04dm3=( )cm3
2800cm3=( )dm3
1325mL=( )L
2040
2.8
1.325
5.
教材P48T5优
6.下面两组数中,每一组都有一个数与其他数不同,
请划去这个数。
教材P48T6优6
6×6×6=216(cm2)
6×6×6=216(cm3)
答:它的表面积是216cm2,它的体积是216cm3。
7.一个棱长为6cm的正方体药盒,它的表面积和体积
分别是多少?
教材P48T7优
200L=200000(cm )
50×50=2500(cm2)
200000÷2500=80(cm)
答:水箱的高是80厘米。
8.一个长方体水箱的容积是200L,这个水箱的底面是一个边长为50cm的正方形,水箱的高是多少厘米?
教材P49T8优
6cm=0.06m
45×28×0.06=75.6(m3)
答:需要75.6立方米的沙土。
教材P49T9优
75.6÷1.5≈51(次)
答:至少需要运51次。
教材P49T9优
15×26×7=2730(cm3)
15×26×40=15600(cm3)
2730×2+15600=21060(cm3)
答:这个旅行包的容积大约是21060cm3。
10.如图,一种旅行包的A,B,C三部分用拉链连接,拆卸方便。这种旅行包可以近似地看成是由右边的三个图形组成的,这个旅行包的容积大约是多少?(单位:cm)
教材P49T10优
5×2×2+12×2×2+12×5=128(dm2)
答:最少需要128dm2的铁皮,这个水槽最多可以盛
120L水。
5×12×2=120(dm )=120(L)
11.做一个如右图的无盖长方体铁皮水槽最少需要多大面积的铁皮?这个水槽最多可以盛多少升水?(单位:dm)
教材P49T11优
50cm=5dm
40cm=4dm
30cm=3dm
5×4×3=60(L)
答:这个油箱能装60升汽油。
12.某汽车油箱的长、宽、高如右图所示。(单位:cm)
(1)这个油箱能装多少升汽油?
教材P49T12优
12.某汽车油箱的长、宽、高如右图所示。(单位:cm)
(2)如果每升汽油可行驶10km,这箱油最多可以供
这辆汽车行驶多少千米?
60×10=600(km)
答:这箱油最多可以供这辆
汽车行驶600千米。
教材P49T12优
不可以。
8个
能,27个。
(答案不唯一)
教材P49T13优
二、基础练习
1.判断对错。
×
(1)一个木头箱子的体积就是它的容积。 ( )
(2)长方体是特殊的正方体。 ( )
(3)棱长是6分米的正方体它的体积和表面积相等。 ( )
(4)用4个棱长1厘米的小正方体可以拼成一个大正方体。 ( )
×
×
×
五年级下册数学课件 长方体和正方体复习课【PPT完美】
单元复习题(1)
二、基础练习
1.判断对错。
√
(5)体积单位和容积单位的进率都是1000。 ( )
(6)把一个正方体铸造成一个长方体,虽然它的形状变了,但是它的体积没有变。 ( )
(7)一块石头完全浸到盛有水的容器里,溢出的水的体积就是石头的体积。 ( )
√
√
五年级下册数学课件 长方体和正方体复习课【PPT完美】
五年级下册数学课件 长方体和正方体复习课【PPT完美】
二、基础练习
面积
长度
6
体积
(1)计量一个长方体的棱长总和用( )单位,计量它的表面积用的是( )单位,计量它的体积用( )单位。
(2)一个正方体的棱长是1厘米,它的表面积是( )平方厘米,它的体积是( )立方厘米。
(3)一辆汽车的油箱能装油72( ),数学书的体积是320( )。
(4)一个长方体长3厘米、宽2厘米、高1厘米,那它的棱长总和是( )。
1
cm3
24厘米
2.填空。
L
五年级下册数学课件 长方体和正方体复习课【PPT完美】
五年级下册数学课件 长方体和正方体复习课【PPT完美】
二、基础练习
3.按要求计算。(单位:cm)
6
5
4
4
4
4
表面积:
体积:
表面积:
体积:
棱长总和:
2×(6 × 5+5 × 4+6 × 4)=148(cm2)
6 × 5 × 4=120(cm3)
6×(4 × 4)=96(cm2)
4 × 4 × 4=64(cm3)
4 × 12=48(cm)
五年级下册数学课件 长方体和正方体复习课【PPT完美】
五年级下册数学课件 长方体和正方体复习课【PPT完美】
二、基础练习
4.一个长方体和一个正方体的棱长总和相等。已知长方体的长、宽、高分别是9 dm、6 dm、3 dm,那么正方体的棱长是多少分米?它们的体积相等吗?
(9+6+3)×4=72(dm) 72÷12=6(dm )
长方体体积:9×6×3=162(dm3)
正方体体积:6×6×6=216(dm3)
不相等
三、易错练习
1.单位换算。
1020
360
3400
1.02 dm3=( )cm3 3.4 m3=( )dm3 ( )mL=0.36 L
2090 cm3=( )L 6.5 m3=( )m3( )dm3
2.09
6
500
五年级下册数学课件 长方体和正方体复习课【PPT完美】
五年级下册数学课件 长方体和正方体复习课【PPT完美】
三、易错练习
C
2.我会选。
(1)一瓶花露水的包装盒上印有“净含量100毫升”的字样,这个“100毫升”是指( )。
A.包装盒的体积 B.包装盒的容积 C.瓶中花露水的体积
(2)一个正方体的棱长扩大到原来的2倍,表面积扩大到原来的( )倍,体积扩大到原来的( )倍。
A.2 B.4 C.8
B
C
五年级下册数学课件 长方体和正方体复习课【PPT完美】
五年级下册数学课件 长方体和正方体复习课【PPT完美】
三、易错练习
A
2.我会选。
(3)一个长方体的棱长之和是180厘米,相交于一个顶点的三条棱的长度和是( )。
A.45厘米 B.30厘米 C.90厘米
(4)从一个长方体中挖掉一个角(如图),它的表面积( )。
A.比原来小 B.比原来大 C.与原来一样大
C
五年级下册数学课件 长方体和正方体复习课【PPT完美】
五年级下册数学课件 长方体和正方体复习课【PPT完美】
三、易错练习
2.我会选。
(5)下列图形不能折成正方体的是( )。
A
B
C
C
五年级下册数学课件 长方体和正方体复习课【PPT完美】
五年级下册数学课件 长方体和正方体复习课【PPT完美】
三、易错练习
3.解决问题。
1.2×1×0.5=0.6(立方米) 0.6立方米=600升 600×0.8=480(千克)
(1)一个油箱里面长1.2米,宽1米,高0.5米,给油箱盛满汽油。如果1升汽油重0.8千克。这个油箱共盛汽油多少千克?
(2)一个游泳池长25米,宽18米,深2米,要给它的四周和底面贴上瓷砖如果每平方米用瓷砖16块,这个游泳池共需瓷砖多少块?
25×18+25×2×2+18×2×2=450+100+72=622 (平方米)
16×622=9952(块)
五年级下册数学课件 长方体和正方体复习课【PPT完美】
五年级下册数学课件 长方体和正方体复习课【PPT完美】
三、易错练习
4.一个长方体的无盖的铁皮水槽,长4 m,宽45 cm,高是1.2 m。
(1)这个铁皮水槽占地面积多大?
(2)需要多少平方米的铁皮?
(3)它的体积是多少?
45 cm=0.45 m 4×0.45=1.8(m2)
4×0.45+(4×1.2+0.45×1.2)×2=12.48(m2)
4×0.45×1.2=2.16(m3)
四、拓展练习
1.一个长方体的底面是一个周长为20 cm的长方形,高为2 cm,如果长和宽的厘米数都是质数,那么这个长方体的体积是多少?
20÷2=10=3+7 3×7×2=42(cm3)
四、拓展练习
正方体的棱长是84÷3÷4=7(厘米)
原长方体的体积是7×7×(7-3)=196(立方厘米)
2.一个长方体,如果高增加3 cm,那么就变成一个正方体。这时表面积比原来增加84 cm2。原来长方体的体积是多少立方厘米?
(1)两个完全一样的长方体拼成一个大长方体,表面积不变。( )
×
判断 。
×
×
×
√
(2)长方体的6个面是完全相同的长方形。 ( )
(3)有六个面的物体不是长方体就是正方体。( )
(5)用八个完全相同的小正方体,可以拼成一个大正方体。( )
(4)棱长为2厘米的正方体,它的棱长之和与它的表面积相等。( )
单元复习题(2)
(1)下列物体中,形状不是长方体的是( )。
A.火柴盒 B.红砖 C.足球 D.木箱
(2)长方体有( )条棱,( )个面,( )个顶点。
A. 4 B.6 C. 8 D. 12
(3)把一个棱长3分米的正方体切成两个相等的长方体,增加的两个面的总面积是( )平方分米。
A.18 B. 9 C. 36 D.以上答案都不对
选择。
C
D
B
C
A
无盖正方体玻璃鱼缸,没有上面,一共有5个面。
做一个棱长为3分米无盖正方体玻璃鱼缸至少需要多大面积的玻璃?
3 ×3 ×5
=9 ×5
=45(平方分米)
答:至少需要45平方分米的玻璃。
下面哪些图形是正方体的展开图?是的画√,错的画×,再利用附页1中的图2试一试。
×
√
√
√
√
×
小兰的房间长4m,宽3m,高3m。除去门窗5m ,房间的墙壁和房顶都贴上墙纸,这个房间至少需要多大面积的墙纸?
4 ×3+(3 ×3+4×3)×2-5
=12+42-5
=49(m )
答:至少需要49平方米的墙纸。
用3个棱长都是1厘米的正方体,拼成一个长方体,这个拼成的长方体表面积是多少?
1 ×3 ×4+1 ×1 ×2
=12+2
=14(平方厘米)
答:这个拼成的长方体表面积是14平方厘米。
用一根36厘米长的铁丝围成一个正方体(接头处不计),这个正方体的表面积是多少平方厘米
(36÷12)×(36÷12)×6
=3×3×6
=54(平方厘米)
答:这个正方体的表面积是54平方厘米。
3个棱长都是30厘米的正方体堆放在墙角处(如下图),露在外面的面积是多少?
30 × 30 × 7
=900×7
= 6300(平方厘米)
答:露在外面的面积是6300 平方厘米。
(1)相交于一个顶点的三条棱的长度分别叫作长方体的( )、( )、( )。
(2)求长方体的棱长总和方法:( )×4+( )×4+( )×4=棱长总和; 也就是( + + )×4=总棱长。
(3)一个长方体的长是10dm,宽是6 dm,高是4 dm,它的棱长总和是( )dm。
(4)一个长方体的棱长总和是80cm,其中长是10cm,宽是5cm,高是( )cm。
填空。
长
宽
高
长
宽
高
长
宽
高
80
5
一个火柴盒长4厘米,宽2厘米,高1.5厘米,做一个完整的火柴盒,至少需要多少纸板?(纸盒厚度不计)
火 柴
外壳 (4×2+2×1.5)×2
= 11×2
=22 ( c㎡ )
火柴盒外壳有上、下、左、右四个面
火柴盒内匣有前、后、左、右、下五个面(缺上面)。
完整的盒子=外+里
22+26=48(c㎡)
答:至少需要48平方厘米的材料。
里盒 (4×1.5+2×1.5)×2+4×2
=9×2+8
=26 (c㎡)
一根绳子长10m,现要捆扎一种礼盒,(如下图)如果接头处要用掉绳子25cm,这根绳子最多可以捆扎几个这样的礼盒?(单位:cm)
10 ×2+8 ×4+15 ×2+25
= 20+32+30+25
= 107(cm)
10m=1000cm
1000÷107=9(个)……37(cm)
答:最多可以捆扎9个这样的礼盒。
40
25
40
淘淘要把一个如下图所示的空包装箱的各个面都贴上彩纸,至少需要多少平方厘米彩纸?(单位:厘米)
40×25×4+40×40×2
=4000+3200
=7200(平方厘米)
答:至少需要7200平方厘米彩纸。
6个棱长都是20厘米的纸箱堆放在墙角处,如下图,露出多少个面?露在外面的面积是多少平方厘米?
露出13个面
20 ×20 ×13
=400 ×13
=5200(平方厘米)
答:露在外面的面积是5200平方厘米.
将一个由5个棱长是10厘米的正方体排成的长方体拆开,如下图,5个正方体的表面积是多少?与长方体的表面积相等吗?与同伴交流。
10 ×10×6×5
=600 ×5
=3000(平方厘米)
答:5个正方体的表面积是3000平方厘米。
与长方形的表面积不相等,拆开后比原来的长方体增加了8个面。
课堂小结
通过本节课的复习你有哪些收获?
名称
内容
项目
长方体
正方体
6个长方形面(最多有2个面是正方形),相对面的面积相等。
12条,每4条长度相等(也可能有8条相等)。每相交于一个顶点的棱分别是长、宽、高。
8个
6个都是完全相同的正方形面
12条,长度都相等。
8个
S表=(a · b+b · h+a · h) ×2
长方体的表面积=(长×宽+宽×高+长×高)×2
长方体的体积=长×宽×高
V= a · b · h
V= S底 · h (其中S底 = a · b
特征
面
棱
顶点
公式
表面积和体积
一、梳理知识
长方体和正方体的特征及公式(一览表)
S表=a2 ×6
正方体的表面积=棱长×棱长×6
V= a · a · a 即a3
长方体的体积=棱长×棱长×棱长
或a2 )
长方体和正方体的特征
形体 相同点 不同点 联系
面 棱 顶点 面的 形状 面的 面积 棱长 正方体是一种特殊的长方体
长方体 6个 12条 8个 6个面都是长方形,有时相对的两个面是正方形 相对的两个面的面积相等 相对的棱的长度相等
正方体 6个面都是正方形 6个面面积都相等 12条棱都相等
长方体和正方体的表面积
S长方体=2ab+2ah+2bh
=2(ab+ah+bh)
S正方体=6a2
长方体和正方体6个面的总面积,叫做它的表面积
a
b
h
a
a
a
长方体和正方体的体积(容积)
体积:物体所占空间的大小。
容积:所能容纳物体空间的大小。
V长方体=abh
V正方体=a3
V=sh
a
b
h
a
a
a
体积(容积)的单位
立方米(m3)
立方分米(dm3)----升(l)
立方厘米(cm3)----毫升(ml)
体积(容积)相邻单位之间的进率是 1000。
把四盒牛奶拼在一起,哪种最省包装材料?
4cm
7cm
10cm
减少的面积:
7×10×6=420(cm2)
减少的面积:
10×7×4+4×10×4=440(cm2)
减少的面积最大
所以最省材料
设计包装盒
★★(1)把一根长30厘米的长方体木料锯成3段(如图),表面积比原来增加了20平方厘米,这根木料原来的体积是多少立方厘米
★★★(2)一个底面是正方形的长方体,把它的侧面展开后得到一个边长是8厘米的正方形。求这个长方体的体积是多少?
选做:
分析
分析
★★(1)把一根长30厘米的长方体木料锯成3段(如图),表面积比原来增加了20平方厘米,这根木料原来的体积是多少立方厘米
选做:
20÷4=5(平方厘米)
30×5=150(平方厘米)
答:这根木材原来的体积是150平方厘米。
1.
小明家准备做一个鱼缸,长1.2米,宽5分米,高6分米。至少需要多少平方米的玻璃材料?它最多可以装水多少升?
2.
装修小明的卧室地面用了360块长50厘米,宽10厘米,厚3厘米的木质地板。请你算算,小明的卧室有多大?至少要用木材多少立方米?
C.深化题
1.2×0.5+0.5×0.6×2+0.6×1.2×2
=0.6+0.3×2+0.72×2
=0.6+0.6+1.44
=2.64 (平方米)
12×5×6
=60×6
=360 (升)
答:至少需要2.64平方米的玻璃材料。最多可以装水360升。
0.5×0.1×360=18 (平方米)
18 ×0.03=0.54 (立方米)
答:小明的卧室有18平方米,至少要用木材0.54立方米。
50厘米=0.5米 10厘米=0.1米 3厘米=0.03米
红岩
红岩
57毫升
R
蓝黑墨水
蓝黑墨水
重庆红岩墨水有限责公司
红岩
6. 5
6
4.3
如图,做一个墨水盒至少需要多少平方厘米的硬纸?这个纸盒的体积是多少?(图上单位:厘米)
1.
棱长6分米的正方体,它的体积和表面积各是多少?
2.
B.基础题
(6.5×4.3+4.3×6+6×6.5)×2
体积:
表面积:
=(27.95+25.8+39)×2
= 92.75×2
= 185.5 (平方厘米)
6.5×4.3×6
=27.95×6
=167.7 (立方厘米)
答:做这个墨水盒至少需要185.5平方厘米的硬纸,这个纸盒的体积是167.7立方厘米。
答:这个正方体的体积是216立方分米,表面积是216平方分米。
62 ×6 =216 (平方分米)
表面积:
63 =216 (立方分米)
体积:
★★★(2)一个底面是正方形的长方体,把它的侧面展开后得到一个边长是8厘米的正方形。求这个长方体的体积是多少?
选做:
8
8
8
2
2
8÷4=2(厘米)
2×2×8=32(立方厘米)
答:这个长方体的体积是108立方厘米。
这个魔方玩具是由一些棱长3厘米的小正方体合成,请迅速计算出该魔方的体积和表面积。
32 × 9 × 6 = 486 (平方厘米)
32 × (9 × 6)
或(3 × 3)2 × 6
33 × 9 ×3= 729 (立方厘米)
33 × (9 ×3)
或(3 × 3)3
D.拓展题
