江苏省金湖中学2012-2013学年高一上学期期末考试数学试题
文档属性
| 名称 | 江苏省金湖中学2012-2013学年高一上学期期末考试数学试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 151.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-23 00:00:00 | ||
图片预览



文档简介
金湖中学2012-2013学年高一上学期期末考试数学试题
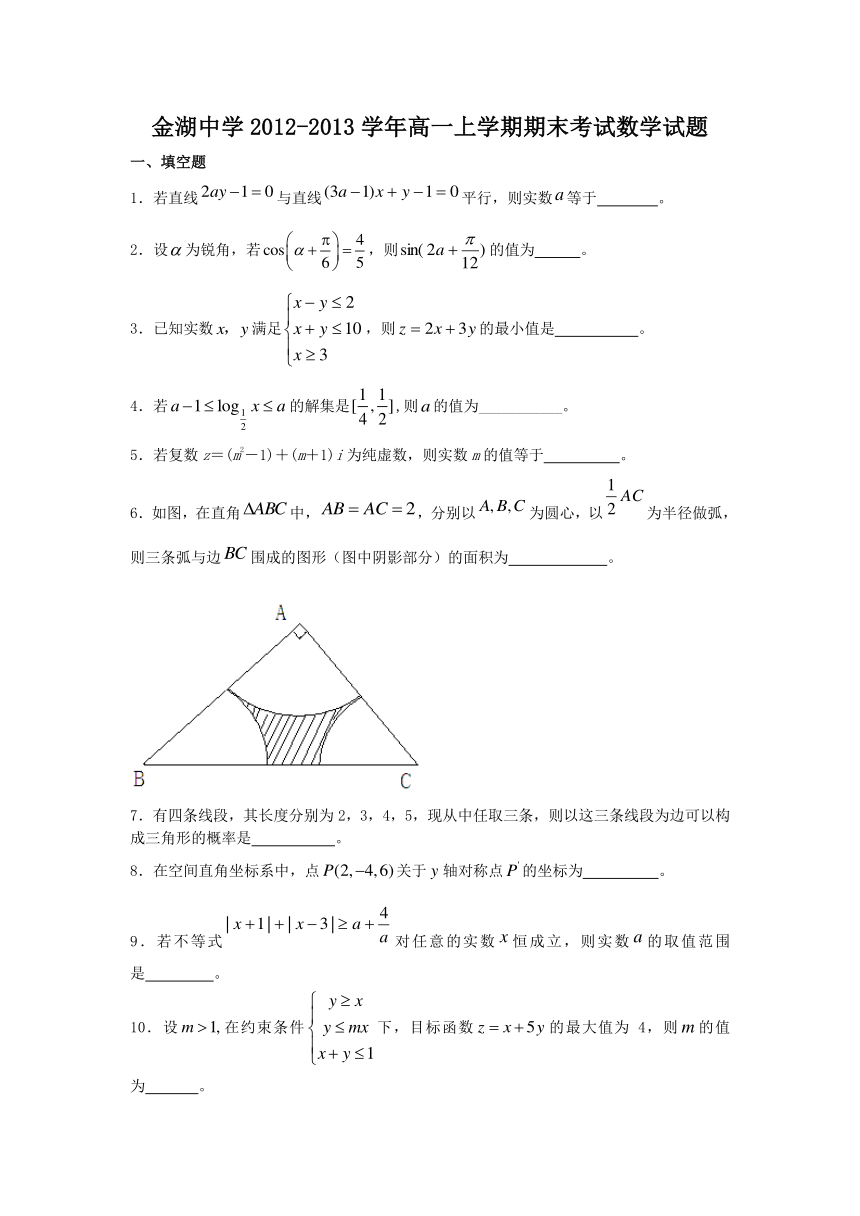
一、填空题
1.若直线与直线平行,则实数等于 。
2.设为锐角,若,则的值为 。
3.已知实数满足,则的最小值是 。
4.若的解集是,则的值为___________。
5.若复数z=(m2-1)+(m+1)i为纯虚数,则实数m的值等于 。
6.如图,在直角中,,分别以为圆心,以为半径做弧,则三条弧与边围成的图形(图中阴影部分)的面积为 。
7.有四条线段,其长度分别为2,3,4,5,现从中任取三条,则以这三条线段为边可以构成三角形的概率是 。
8.在空间直角坐标系中,点关于轴对称点的坐标为 。
9.若不等式对任意的实数恒成立,则实数的取值范围是 。
10.设在约束条件下,目标函数的最大值为4,则的值为 。
11.圆心在轴上,且过两点A(1,4),B(3,2)的圆的方程为 。
12.分别是双曲线的左、右焦点,P为双曲线右支上一点,I是的内心,且,则= _________。
13.已知点A,B是双曲线上的两点,O为原点,若,则点O到
直线AB的距离为 。
14.,,,且,求实数的取值范围 。
二、解答题
15.已知命题:“若,则二次方程没有实根”.(1)写出命题的否命题;(2)判断命题的否命题的真假,并证明你的结论.
16.已知或;;是的充分而不必要条件,求实数的取值范围.
17.记公差d≠0的等差数列{an}的前n项和为Sn,已知a1=2+,S3=12+.
(1)求数列{an}的通项公式an及前n项和Sn;
(2)记bn=an-,若自然数n1,n2,…,nk,…满足1≤n1<n2<…<nk<…,并且,,…,,…成等比数列,其中n1=1,n2=3,求nk(用k表示);
(3)试问:在数列{an}中是否存在三项ar,as,at(r<s<t,r,s,t∈N*)恰好成等比数列?若存在,求出此三项;若不存在,请说明理由.
18.已知离心率为的双曲线,双曲线的一个焦点到
渐近线的距离是
(1)求双曲线的方程
(2)过点的直线与双曲线交于、两点,交轴于点,当
,且时,求直线的方程
19.已知等差数列{}中,求{}前n项和.
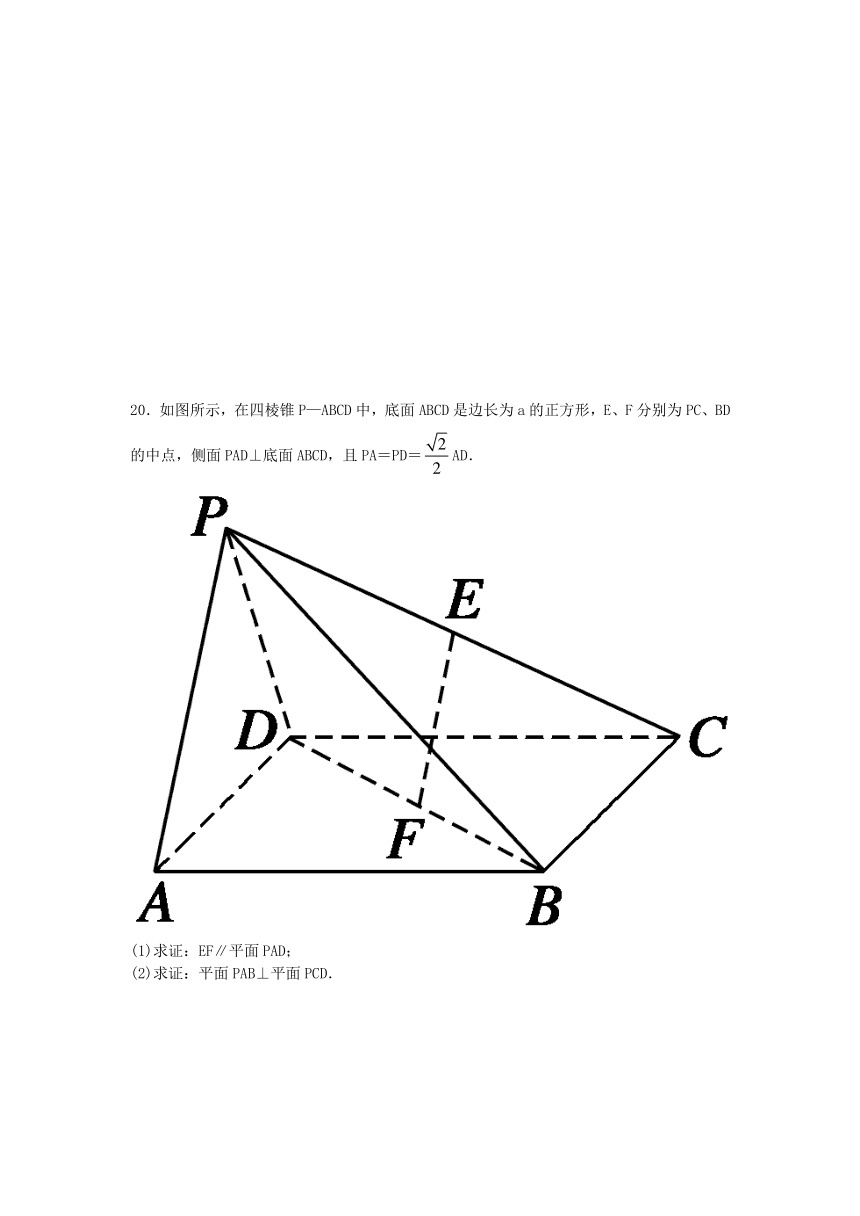
20.如图所示,在四棱锥P—ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=AD.
(1)求证:EF∥平面PAD;
(2)求证:平面PAB⊥平面PCD.
参考答案
1.
2.
【解析】
,,
3.9
4.
【解析】解:因为的解集是,可以利用对数函数的性质可知参数a的值为2.
5.m=1
【解析】
解:复数z=(m2-1)+(m+1)i
[1]
Z是实数时,必有:
m+1=0
∴m=-1
[[2]]
当z是虚数时,必有:
m+1≠0
∴此时,m≠-1
[[3]]
当z是纯虚数时,必有:
m2-1=0且m+1≠0
∴此时,有m=1
6.
7.
8.
9.
10.3
11.
【解析】
试题分析:因为圆心在轴上,所以设圆心坐标为(m,0),半径为r,则圆的方程为(x-m)2+y2=r2,因为圆经过两点A(1,4)、B(3,2),所以,解得:m=-1,r2=20,所以圆的方程为(x+1)2+y2=20。
考点:圆的方程的求法。
点评:本题考查的重点是圆的标准方程的求法,解题的关键是根据设出的圆心坐标和半径表示出圆的方程,利用待定系数法求出圆心和半径。
12.
【解析】
试题分析:设内切圆的半径为r,则根据双曲线的标准方程知
考点:本小题主要考查双曲线定义及标准方程的应用,考查学生转化问题的能力数数形结合数学思想的应用.
点评:解决此题的关键在于根据已知条件转化成,从而利于双曲线的标准方程进行求解.
13.
【解析】
试题分析:,取分别位于第一第四象限,斜率为1,
斜率为,,代入双曲线可求得直线为
,点O到直线AB的距离为
考点:直线与双曲线的位置关系及点到直线距离
点评:本题作为一道小题,采用特殊值特殊位置的方法求解方便易行
14.
【解析】
【错解分析】此题容易错填,错误原因是漏掉考虑A为空集的情况。
【正解】
或
15.(1)同解析;(2)命题的否命题是真命题.
【解析】(1)命题的否命题:“若,则二次方程有实根”
(2)命题的否命题是真命题.证明如下:
∵,∴,
∴,
二次方程有实根,
∴该命题是真命题.
16.的取值范围为(3,+)
【解析】本试题主要是考查了充分条件的求解,以及数轴法表示集合的综合运用。
因为,或;,∵,∴,则可以解出参数m的范围
17.(1)因为a1=2+,S3=3a1+3d=12+,所以d=2.
所以an=a1+(n-1)d=2n+, Sn==n2+(+1)n.
(2)因为bn=an-=2n,所以=2nk.又因为数列{}的首项=,
公比,所以.所以2nk,即nk.
(3)假设存在三项ar,as,at成等比数列,则,
即有,整理得.
若,则,因为r,s,t∈N*,所以是有理数,
这与为无理数矛盾;
若,则,从而可得r=s=t,这与r<s<t矛盾.
综上可知,不存在满足题意的三项ar,as,at.
18.解:(1) ………………………………………1分
右焦点到渐近线的距离
………………………………3分
从而得 双曲线方程是………………………5分
(2)设,直线,则
是双曲线上的点
整理得 同理……9分
是方程的两个根
, …………①
…………………②
①代入② 解得
方程为或 ……………………………12分
解法二:设,
由得
………………①
由得,同理
,
解得满足①方程为或
【解析】略
19.解:设的公差为,则.
即
解得
因此
20.(1) 见解析(2) 见解析
【解析】本题考查直线与平面垂直的判定,直线与平面平行的判定的应用,考查逻辑推理能力.
(1)证明:连接AC,则F是AC的中点,E为PC 的中点,证明EF∥PA,留言在线与平面平行的判定定理证明EF∥平面PAD;
(2)先证明CD⊥PA,然后证明PA⊥PD.利用直线与平面垂直的判定定理证明PA⊥平面PCD,从而得到证明。
证明:(1)连结AC,则F是AC的中点,E为PC的中点,
故在△CPA中,EF∥PA, ……3分
又∵PA?平面PAD,EF?平面PAD,
∴EF∥平面PAD. ……6分
(2)∵平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,
又∵CD⊥AD,∴CD⊥平面PAD,∴CD⊥PA. ……8分
又PA=PD=AD,∴△PAD是等腰直角三角形,且∠APD=,即PA⊥PD.
又∵CD∩PD=D,∴PA⊥平面PCD.
又∵PA?平面PAB,∴平面PAB⊥平面PCD. ……12分
一、填空题
1.若直线与直线平行,则实数等于 。
2.设为锐角,若,则的值为 。
3.已知实数满足,则的最小值是 。
4.若的解集是,则的值为___________。
5.若复数z=(m2-1)+(m+1)i为纯虚数,则实数m的值等于 。
6.如图,在直角中,,分别以为圆心,以为半径做弧,则三条弧与边围成的图形(图中阴影部分)的面积为 。
7.有四条线段,其长度分别为2,3,4,5,现从中任取三条,则以这三条线段为边可以构成三角形的概率是 。
8.在空间直角坐标系中,点关于轴对称点的坐标为 。
9.若不等式对任意的实数恒成立,则实数的取值范围是 。
10.设在约束条件下,目标函数的最大值为4,则的值为 。
11.圆心在轴上,且过两点A(1,4),B(3,2)的圆的方程为 。
12.分别是双曲线的左、右焦点,P为双曲线右支上一点,I是的内心,且,则= _________。
13.已知点A,B是双曲线上的两点,O为原点,若,则点O到
直线AB的距离为 。
14.,,,且,求实数的取值范围 。
二、解答题
15.已知命题:“若,则二次方程没有实根”.(1)写出命题的否命题;(2)判断命题的否命题的真假,并证明你的结论.
16.已知或;;是的充分而不必要条件,求实数的取值范围.
17.记公差d≠0的等差数列{an}的前n项和为Sn,已知a1=2+,S3=12+.
(1)求数列{an}的通项公式an及前n项和Sn;
(2)记bn=an-,若自然数n1,n2,…,nk,…满足1≤n1<n2<…<nk<…,并且,,…,,…成等比数列,其中n1=1,n2=3,求nk(用k表示);
(3)试问:在数列{an}中是否存在三项ar,as,at(r<s<t,r,s,t∈N*)恰好成等比数列?若存在,求出此三项;若不存在,请说明理由.
18.已知离心率为的双曲线,双曲线的一个焦点到
渐近线的距离是
(1)求双曲线的方程
(2)过点的直线与双曲线交于、两点,交轴于点,当
,且时,求直线的方程
19.已知等差数列{}中,求{}前n项和.
20.如图所示,在四棱锥P—ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=AD.
(1)求证:EF∥平面PAD;
(2)求证:平面PAB⊥平面PCD.
参考答案
1.
2.
【解析】
,,
3.9
4.
【解析】解:因为的解集是,可以利用对数函数的性质可知参数a的值为2.
5.m=1
【解析】
解:复数z=(m2-1)+(m+1)i
[1]
Z是实数时,必有:
m+1=0
∴m=-1
[[2]]
当z是虚数时,必有:
m+1≠0
∴此时,m≠-1
[[3]]
当z是纯虚数时,必有:
m2-1=0且m+1≠0
∴此时,有m=1
6.
7.
8.
9.
10.3
11.
【解析】
试题分析:因为圆心在轴上,所以设圆心坐标为(m,0),半径为r,则圆的方程为(x-m)2+y2=r2,因为圆经过两点A(1,4)、B(3,2),所以,解得:m=-1,r2=20,所以圆的方程为(x+1)2+y2=20。
考点:圆的方程的求法。
点评:本题考查的重点是圆的标准方程的求法,解题的关键是根据设出的圆心坐标和半径表示出圆的方程,利用待定系数法求出圆心和半径。
12.
【解析】
试题分析:设内切圆的半径为r,则根据双曲线的标准方程知
考点:本小题主要考查双曲线定义及标准方程的应用,考查学生转化问题的能力数数形结合数学思想的应用.
点评:解决此题的关键在于根据已知条件转化成,从而利于双曲线的标准方程进行求解.
13.
【解析】
试题分析:,取分别位于第一第四象限,斜率为1,
斜率为,,代入双曲线可求得直线为
,点O到直线AB的距离为
考点:直线与双曲线的位置关系及点到直线距离
点评:本题作为一道小题,采用特殊值特殊位置的方法求解方便易行
14.
【解析】
【错解分析】此题容易错填,错误原因是漏掉考虑A为空集的情况。
【正解】
或
15.(1)同解析;(2)命题的否命题是真命题.
【解析】(1)命题的否命题:“若,则二次方程有实根”
(2)命题的否命题是真命题.证明如下:
∵,∴,
∴,
二次方程有实根,
∴该命题是真命题.
16.的取值范围为(3,+)
【解析】本试题主要是考查了充分条件的求解,以及数轴法表示集合的综合运用。
因为,或;,∵,∴,则可以解出参数m的范围
17.(1)因为a1=2+,S3=3a1+3d=12+,所以d=2.
所以an=a1+(n-1)d=2n+, Sn==n2+(+1)n.
(2)因为bn=an-=2n,所以=2nk.又因为数列{}的首项=,
公比,所以.所以2nk,即nk.
(3)假设存在三项ar,as,at成等比数列,则,
即有,整理得.
若,则,因为r,s,t∈N*,所以是有理数,
这与为无理数矛盾;
若,则,从而可得r=s=t,这与r<s<t矛盾.
综上可知,不存在满足题意的三项ar,as,at.
18.解:(1) ………………………………………1分
右焦点到渐近线的距离
………………………………3分
从而得 双曲线方程是………………………5分
(2)设,直线,则
是双曲线上的点
整理得 同理……9分
是方程的两个根
, …………①
…………………②
①代入② 解得
方程为或 ……………………………12分
解法二:设,
由得
………………①
由得,同理
,
解得满足①方程为或
【解析】略
19.解:设的公差为,则.
即
解得
因此
20.(1) 见解析(2) 见解析
【解析】本题考查直线与平面垂直的判定,直线与平面平行的判定的应用,考查逻辑推理能力.
(1)证明:连接AC,则F是AC的中点,E为PC 的中点,证明EF∥PA,留言在线与平面平行的判定定理证明EF∥平面PAD;
(2)先证明CD⊥PA,然后证明PA⊥PD.利用直线与平面垂直的判定定理证明PA⊥平面PCD,从而得到证明。
证明:(1)连结AC,则F是AC的中点,E为PC的中点,
故在△CPA中,EF∥PA, ……3分
又∵PA?平面PAD,EF?平面PAD,
∴EF∥平面PAD. ……6分
(2)∵平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,
又∵CD⊥AD,∴CD⊥平面PAD,∴CD⊥PA. ……8分
又PA=PD=AD,∴△PAD是等腰直角三角形,且∠APD=,即PA⊥PD.
又∵CD∩PD=D,∴PA⊥平面PCD.
又∵PA?平面PAB,∴平面PAB⊥平面PCD. ……12分
同课章节目录
