双减背景下苏教版四年级数学(下)第一单元质量测试卷(含答案)
文档属性
| 名称 | 双减背景下苏教版四年级数学(下)第一单元质量测试卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 666.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-15 15:28:18 | ||
图片预览



文档简介
第I卷(选择题)
一、选择题
1.下面图形中,对称轴数量最多的是( )。
A. B. C. D.
2.下面图形有( )条对称轴。
A.2 B.4 C.5 D.6
3.下面说法正确的有( )个。
①拉抽屉和升降梯的运动都是平移现象。
②图形的平移和旋转都只改变图形的位置,不改变图形的形状和大小。
③把三角形对折后折痕两边的部分一定能完全重合。
④字母E只有一条对称轴。
A.1 B.2 C.3 D.4
4.下面说法正确的是( )。
A.旋转改变图形的形状和大小 B.平移改变图形的形状和大小
C.平移和旋转都不改变图形的形状和大小 D.A和B都对
5.将一个正方形对折两次,不可能得到的图形是( )。
A.正方形 B.三角形 C.长方形 D.平行四边形
6.这是一个电风扇开关,数字表示风速档。现在风扇在“1”档运行,如果要关闭,可将旋钮( )。
A.按顺时针方向旋转90° B.按顺时针方向旋转120°
C.按逆时针方向旋转90° D.按逆时针方向旋转120°
7.下图中经过平移可以完全重合的是( )。
A. B. C. D.
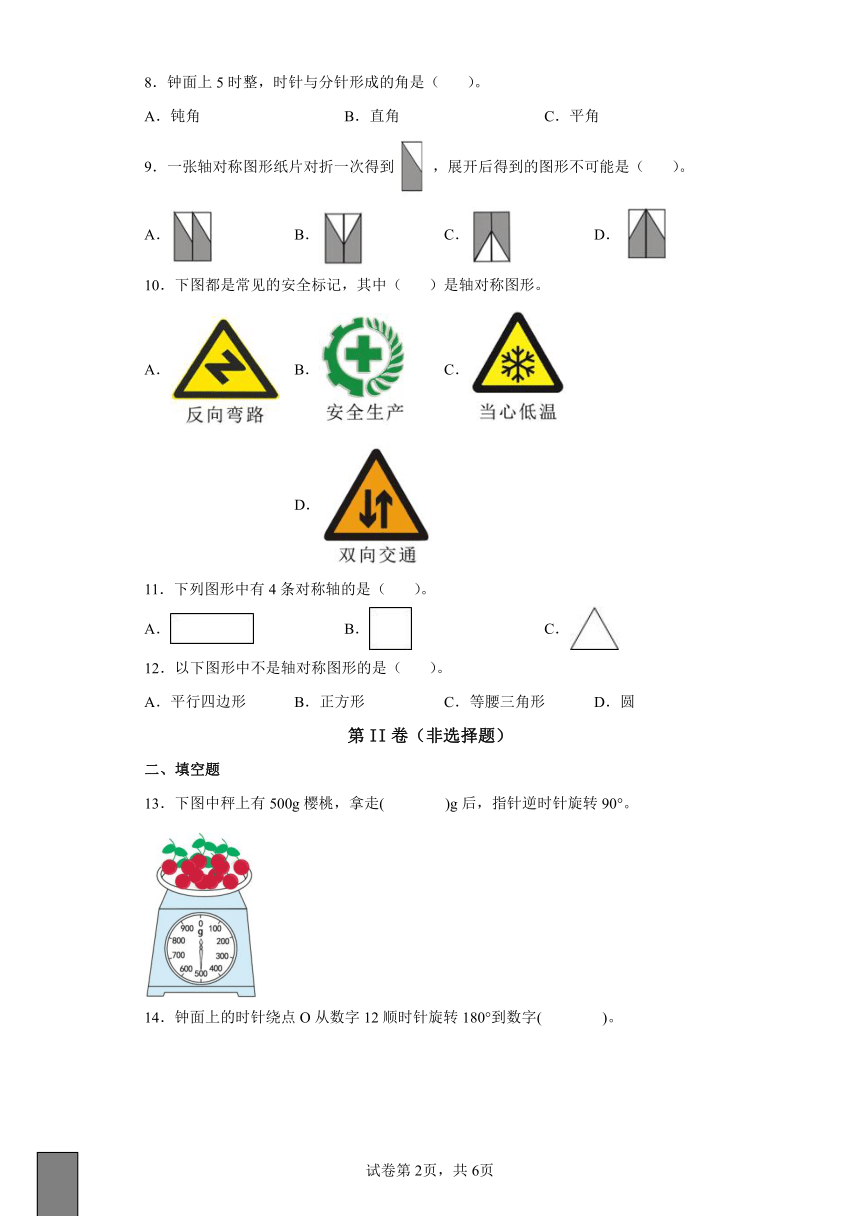
8.钟面上5时整,时针与分针形成的角是( )。
A.钝角 B.直角 C.平角
9.一张轴对称图形纸片对折一次得到,展开后得到的图形不可能是( )。
A. B. C. D.
10.下图都是常见的安全标记,其中( )是轴对称图形。
A. B. C. D.
11.下列图形中有4条对称轴的是( )。
A. B. C.
12.以下图形中不是轴对称图形的是( )。
A.平行四边形 B.正方形 C.等腰三角形 D.圆
第II卷(非选择题)
二、填空题
13.下图中秤上有500g樱桃,拿走( )g后,指针逆时针旋转90°。
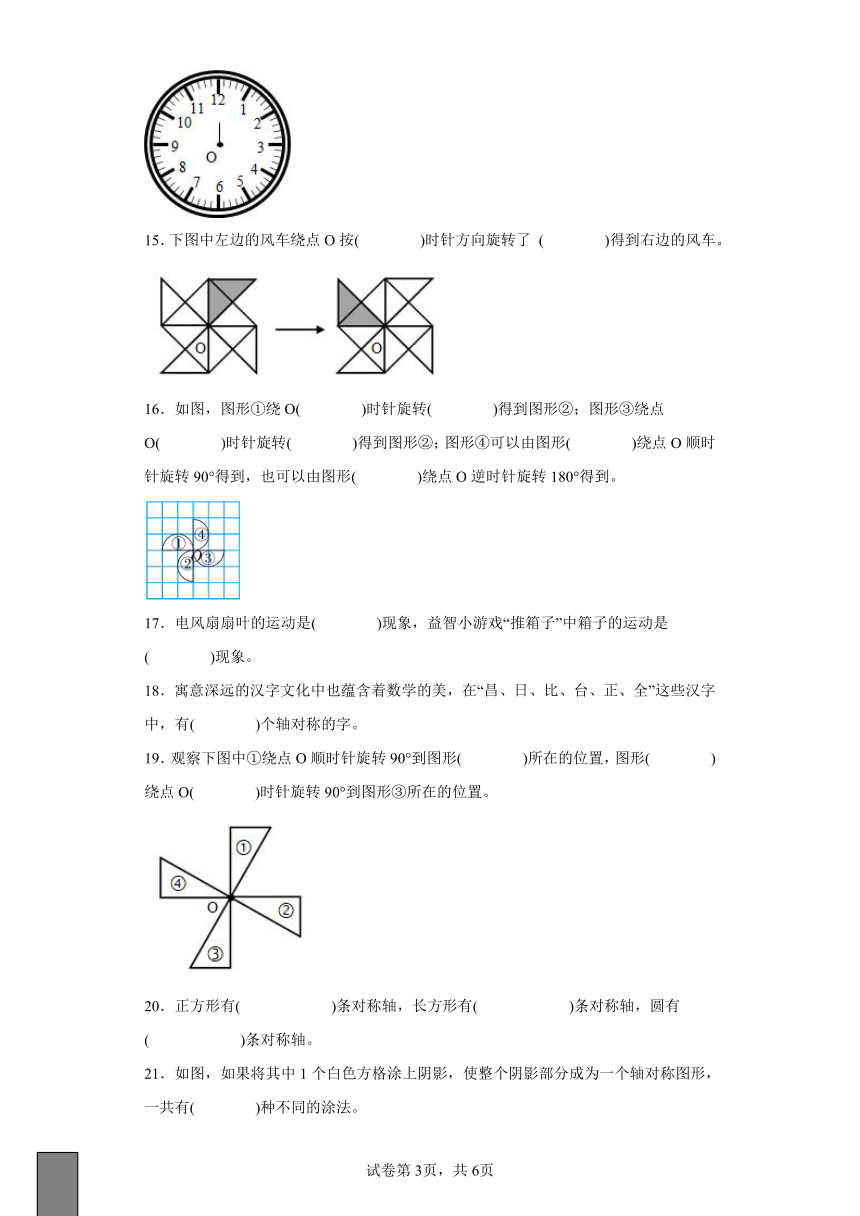
14.钟面上的时针绕点O从数字12顺时针旋转180°到数字( )。
15.下图中左边的风车绕点O按( )时针方向旋转了 ( )得到右边的风车。
16.如图,图形①绕O( )时针旋转( )得到图形②;图形③绕点O( )时针旋转( )得到图形②;图形④可以由图形( )绕点O顺时针旋转90°得到,也可以由图形( )绕点O逆时针旋转180°得到。
17.电风扇扇叶的运动是( )现象,益智小游戏“推箱子”中箱子的运动是( )现象。
18.寓意深远的汉字文化中也蕴含着数学的美,在“昌、日、比、台、正、全”这些汉字中,有( )个轴对称的字。
19.观察下图中①绕点O顺时针旋转90°到图形( )所在的位置,图形( )绕点O( )时针旋转90°到图形③所在的位置。
20.正方形有( )条对称轴,长方形有( )条对称轴,圆有( )条对称轴。
21.如图,如果将其中1个白色方格涂上阴影,使整个阴影部分成为一个轴对称图形,一共有( )种不同的涂法。
22.早晨7点10分,妈妈叫醒小明,让他起床,可小明从镜子中看到的时刻还没有到起床的时刻,他对妈妈说:“还早呢!”小明误以为当时是( )点( )分。
三、判断题
23.长方形、正方形、平行四边形和圆都是轴对称图形。( )
24.圆有无数条对称轴。( )
25.轴对称图形上的对称点到对称轴的距离相等。( )
26.所有的三角形都是轴对称图形。( )
27.电梯上升是旋转现象,钟表指针转动是平移现象。( )
四、连线题
28.下面图案各是从哪张纸上剪下来的?请连线。
五、作图题
29.画出下面各图形的所有对称轴。
30.根据对称轴画出下面轴对称图形的另一半。
31.按要求画出图形。
(1)先将小船向左平移6格,再向下平移5格。
(2)把三角形绕点B逆时针旋转90°。
六、解答题
32.王爷爷家的一棵小树被大风刮倒了(如图),王爷爷想把小树扶正。他该怎么办?
33.你能通过卡片的平移或旋转将图2“还原”成图1吗?写一写你的“还原过程”。
34.先画出下列图形所有的对称轴,再数一数,填一填。
( )条 ( )条 ( )条 ( )条
35.(1)把长方形绕点A逆时针旋转90°,画出旋转后的图形。
(2)如果每个小方格的边长是1厘米,那么在旋转过程中点B经过的路线长( )厘米。
36.按要求填一填、画一画.
(1)向 平移了 格。
(2)向 平移了 格。
(3)将向左平移4格。
37.作图.
(1)以直线MN为对称轴作图A的轴对称图形,得到图形B;
(2)将图形B绕点O逆时针旋转90度,得到图形C;
(3)将图形C向右平移6格,得到图形D.
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
试卷第1页,共3页
试卷第2页,共6页
参考答案:
1.C
【解析】
【分析】
依据轴对称图形的意义,即在同一个平面内,一个图形沿某条直线对折,对折后的两部分都能完全重合,则这个图形就是轴对称图形,这条直线就是其对称轴,据此解答即可。
【详解】
A.有2条对称轴;
B.有1条对称轴;
C.有4条对称轴;
D.不是轴对称图形;
故答案为:C
【点睛】
此题主要考查了轴对称图形的对称轴数量,掌握对称轴的含义是解答本题的关键。
2.B
【解析】
【分析】
对称轴:如果一个图形沿一条直线对折,直线两侧的部分能够完全重合,这个图形就是轴对称图形,这条直线就是它的对称轴。
【详解】
由图可知,这个图有4条对称轴。
故答案为:B
【点睛】
明确轴对称图形的特点是解答本题的关键。
3.C
【解析】
【分析】
平移是物体作直线运动,旋转是物体绕某一点作圆周运动;三角形对折后两部分是不是一定能完全重合,得看这个三角形是什么三角形;把一个图形沿着一条直线折叠,这条直线两边的图形能够完全重合,这个图形就是轴对称图形,这条直线就是对称轴。
【详解】
①拉抽屉和升降梯的运动都是平移现象,这句话是对的。
②图形的平移和旋转都只改变图形的位置,不改变图形的形状和大小,这句话是对的。
③把三角形对折后折痕两边的部分一定能完全重合,不一定。
④字母E只有一条对称轴,这句话是对的。
故答案为:C
【点睛】
重点考查学生对于平移与旋转的理解。
4.C
【解析】
【分析】
根据平移和旋转的判断方法:平移是指在平面内将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动。旋转是指在平面内将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。平移和旋转都是物体的整体运动,所以大小和形状都不会改变。
【详解】
根据平移和旋转运动特点,二者都是整体运动,所以平移和旋转都不改变图形的形状和大小。
故答案为:C
【点睛】
本题主要考查平移和旋转运动的特点,牢记平移和旋转都不改变图形的形状和大小。
5.D
【解析】
【分析】
根据正方形对折后的图形,画出两次对折之后的图形如下(用阴影部分表示),据此即可解答问题。
【详解】
根据分析可得,选项A、B、C中图形都可以利用正方形进行两次对折后得出,只有选项D不能由正方形对折两次得出。
故答案为:D
【点睛】
本题主要考查学生的动手能力及空间想象能力,对于此类问题,学生只要亲自动手操作,答案就会很直观地呈现。
6.C
【解析】
【分析】
关在1的左上位置,应按照逆时针方向旋转90°即可将风扇关了。
【详解】
根据分析按逆时针方向旋转90°。
故答案为:C
【点睛】
和时针旋转方向相同为顺时针方向,和时针旋转方向相反是逆时针方向。
7.B
【解析】
【分析】
物体或图形平移后,它们的形状、大小、方向都不改变,只是位置发生了变化。
【详解】
根据分析,下面图形中经过平移可以重合的是。
故答案为:B
【点睛】
本题考查了平移与平移现象,决定平移后图形的位置的要素:一是平移的方向,二是平移的距离。
8.A
【解析】
【分析】
5时整,时针指向5,分针指向12,12和5之间有5个大格,钟面上一个大格的度数是:360÷12=30°,因此用30×5即可。然后根据角的分类标准选择即可。
【详解】
30×5=150°
90°<150°<180°
因此时针与分针形成的角是钝角。
故答案为:A
【点睛】
此题考查的是对钟面指针的认识,角的分类标准,以及三位数与两位数的除法计算,要熟练掌握。
9.A
【解析】
【分析】
一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴,据此解答。
【详解】
根据轴对称的定义可知,、、对折后是,对折后不重合。
故答案为:A
【点睛】
掌握轴对称图形的定义是解答此题的关键。
10.C
【解析】
【分析】
轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,这条直线就叫做对称轴。本题直接根据轴对称图形的定义和特征进行选择即可。
【详解】
根据轴对称图形的性质可知,轴对称图形的是第三个图形。
故答案为:C。
【点睛】
本题考查学生对图形轴对称的理解,而且考查学生平时观察事物的细心程度。
11.B
【解析】
【分析】
分别画出各选项对称轴即可解答。
【详解】
A.,有2条对称轴;
B.,有4条对称轴;
C.,有3条对称轴;
故答案为:B。
【点睛】
熟练掌握常见图形的对称条数是解答本题的关键。
12.A
【解析】
【分析】
一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形。
【详解】
平行四边形沿一条直线折叠,直线两旁的部分不能够完全重合,因此平行四边形不是轴对称图形。
故答案为:A
【点睛】
熟练掌握轴对称图形是解答本题的关键。
13.250
【解析】
【分析】
旋转90°是180°的一半,逆时针旋转表示樱桃质量变轻,所以拿走一半的樱桃即可。
【详解】
根据分析可得:500÷2=250(g),所以拿走250g后,指针逆时针旋转90°。
【点睛】
解答此题的关键是明确逆时针旋转90°就是拿走500g的一半。
14.6
【解析】
【分析】
时针旋转一周是360°,钟面上共12个大格,每相邻两个数字间隔的度数是360°÷12=30°,时针从数字12顺时针旋转180°,共有180°÷30°=6(个)间隔, 所以钟面上的时针绕点O从数字12顺时针旋转180°到数字6。
【详解】
根据分析可知:钟面上的时针绕点O从数字12顺时针旋转180°到数字6。
【点睛】
解答此题的关键是明确钟面上一个大格的度数是30°。
15. 逆 90°
【解析】
【分析】
在平面内,一个图形绕着一个定点旋转一定的角度得到另一个图形的变化叫做旋转。
【详解】
图中左边的风车绕点O按逆时针方向旋转了90°得到右边的风车。
【点睛】
熟练掌握旋转的定义是解答此题的关键。
16. 逆 90° 顺 90° ① ②
【解析】
【分析】
在平面内,一个图形绕着一个定点旋转一定的角度得到另一个图形的变化叫做旋转。
【详解】
如图,图形①绕O逆时针旋转90°得到图形②;图形③绕点O顺时针旋转90°得到图形②;图形④可以由图形①绕点O顺时针旋转90°得到,也可以由图形②绕点O逆时针旋转180°得到。
【点睛】
熟练掌握旋转的定义是解答此题的关键。
17. 旋转 平移
【解析】
【分析】
在平面内,一个图形绕着一个定点旋转一定的角度得到另一个图形的变化叫做旋转。在同一平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移。
【详解】
电风扇扇叶的运动是旋转现象,益智小游戏“推箱子”中箱子的运动是平移现象。
【点睛】
熟练掌握旋转、平移的定义是解答此题的关键。
18.3
【解析】
【分析】
依据轴对称图形的意义,即在同一个平面内,一个图形沿某条直线对折,对折后的两部分都能完全重合,则这个图形就是轴对称图形,这条直线就是其对称轴,据此解答即可。
【详解】
在“昌、日、比、台、正、全”这些汉字中,有昌、日、全共3个轴对称的字。
【点睛】
掌握对称轴的含义是解答本题的关键。
19. ② ② 顺
【解析】
【分析】
图①到图②得按顺时针方向旋转,图②到图③也得按顺时针方向旋转,图①到图②之间的角度是90°,图②到图③之间的角度是90°,据此填空。
【详解】
观察下图中①绕点O顺时针旋转90°到图形②所在的位置,图形②绕点O顺时针旋转90°到图形③所在的位置。
【点睛】
顺时针方向即与时针旋转方向相同的方向。
20. 4 2 无数
【解析】
【分析】
应熟记常见图形的对称轴数量,例如:等腰梯形有1条对称轴,等边三角形有3条对称轴,等腰三角形有1条对称轴,平行四边形没有对称轴,正方形有4条对称轴,长方形有2条对称轴,圆有无数条对称轴。
【详解】
由分析可知:正方形有4条对称轴,长方形有2条对称轴,圆有无数条对称轴。
【点睛】
本题主要考查学生对常见图形对称轴条数的掌握。
21.4
【解析】
【分析】
根据轴对称的的特点,对折后折痕两边的部分能够完全重合的图形是轴对称图形,据此解答即可。
【详解】
如图所示,如果将其中1个白色方格涂上阴影,使整个阴影部分成为一个轴对称图形,一共有4种不同的涂法。
【点睛】
掌握轴对称图形的特点是解题的关键,画出图形更加形象、具体,是比较好的方法。
22. 4 50
【解析】
【分析】
根据镜面对称的特征,镜中的景物与实际景物上下前后方向一致,左右方向相反,大小不变,且关于镜面对称。据此可知,实际是7点10分,时针在7和8之间,分针指向10。则小明看到时针在4和5之间,分针指向10。
【详解】
如图所示,小明误以为当时是4点50分。
【点睛】
此题主要明白镜面对称的特点是:上下前后方向一致,左右方向相反,镜中与实际景物大小不变。
23.×
【解析】
【分析】
轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,这条直线就叫做对称轴。
【详解】
平行四边形不是轴对称图形,所以说法错误。
故答案为:×
【点睛】
平行四边形这个图形,无论从哪个角度想象一根直线,直线两旁的部分都不能完全重合,因此它不是轴对称图形。
24.√
【解析】
【详解】
一个平面图形沿着一条直线对折后,能够完全重合,这个图形叫做轴对称图形,这条直线叫做对称轴。据此,根据圆的特点,可以知道圆有无数条对称轴。
故此说法正确。
25.√
【解析】
【分析】
根据轴对称图形的特点,即轴对称图形是指一个图形沿一条直线折叠后直线两旁的部分能够完全重合,这条直线就是这个轴对称图形的对称轴;轴对称图形中,对称点到对称轴的距离相等。
【详解】
根据轴对称图形定义可知,轴对称图形上的对称点到对称轴的距离相等。
故答案为:√
【点睛】
正确理解对称轴的定义是解题关键。
26.×
【解析】
【分析】
依据轴对称图形的意义,即在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴,据此即可进行判断。
【详解】
等腰三角形和等边三角形沿底边及其对应顶点所在的直线对折,对折后的两部分都能完全重合,则等腰三角形和等边三角形是轴对称图形。而题干中没说明是什么三角形,所以不能判定这个三角形就是轴对称图形。
故答案为:×
【点睛】
本题掌握轴对称图形的认识是解题关键。
27.×
【解析】
【分析】
平移:在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。平移后图形的位置改变,形状、大小、方向不变。旋转:在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫作图形的旋转。据此解答即可。
【详解】
电梯上升是平移现象,钟表指针转动是旋转现象。
所以判断错误。
【点睛】
本题考查了平移与旋转的现象的判断,熟练掌握平移和旋转的区别是解答本题的关键。
28.见详解
【解析】
【分析】
第二行图形,第1个缺的是的一半,第2个缺的是的一半,第2个缺的是的一半,第4个缺的是的一半,据此连接。
【详解】
【点睛】
可以先把第二行图形中缺失部分的轴对称图形画出。
29.见详解
【解析】
【分析】
如果一个图形沿着一条直线对折,直线两边的图形能够完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。据此作图。
【详解】
【点睛】
本题是考查画轴对称图形对称轴,轴对称图形的对称轴实际上就是对称点连线的垂直平分线。
30.见详解
【解析】
【分析】
找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【详解】
【点睛】
本题考查的是补全轴对称图形,找到关键点,做出关键点的对称点是关键。
31.见详解
【解析】
【分析】
(1)图形的平移作图,需要确定关键点、平移方向与平移距离,根据平移的特征,把小船的各顶点分别先向左平移6格,再向下平移5格,再依次连结各点即可得到平移后的图形。
(2)旋转作图的三个关键要素为:旋转中心、旋转方向与旋转角度,然后再作图。本题的旋转中心为点B,转转方向为逆时针方向,旋转角度为90度。据此作图即可。
【详解】
根据分析,作图如下:
【点睛】
作平移后的图形、作旋转一定度数后的图形的关键是对应点位置的确定。
32.他应当将树干绕点O顺时针旋转30°扶正
【解析】
【分析】
根据旋转的性质可知,把小树扶正,这种变换相当于以O为中心的旋转变换,旋转到和地面的夹角是90°。
【详解】
扶正时小树和地面时垂直的,夹角是90°,90°-60°=30°
所以他应当将树干绕点O顺时针旋转30°扶正。
【点睛】
本题考查旋转的性质,要注意旋转的三要素:①定点—旋转中心;②旋转方向;③旋转角度。
33.见详解
【解析】
【分析】
仔细观察图2中共有4个图片,4个图片的位置都不对,图2种右上角的图形正确的位置是左上角,所以应向左平移1格,图2中左上角的图应在左下角的位置,所以应将图2中左上角的图向下平移1格,图2中右下角的图正确的位置应是右上角,所以应把图2中右下角的图形向上平移1格,图2中左下角的图不仅位置不对方向也不对,可将其绕右下角的顶点顺时针旋转90°即可到达正确的位置。
【详解】
将图2左上角的图形向下平移1格,右上角的图形向左平移1格,右下角的图形向上平移1格,左下角的图形绕其右下角的顶点顺时针旋转90°即可得到图1。
【点睛】
图2中的4个小图一个一个的放在其对应的位置,可通过平移或旋转。
34.见详解
【解析】
【分析】
第1个图,横竖各一条对称轴,过两个叶片形中间还有2条对称轴;第2个图,过三角形的3个顶点有3条对称轴;第3个图,同时过两圆圆心的直线是1条对称轴,过两圆重合部分的直线是一条对称轴;第4图,过每个圆的圆心能作1条对称轴。
【详解】
【点睛】
把一个图形沿着一条直线折叠,直线两边的图形能够完全重合,这条直线就是这个图形的对称轴。
35.(1)见详解
(2)4.71
【解析】
【分析】
(1)根据旋转的意义,找出图中长方形的4个关键处,再画出绕A按逆时针方向旋转90度后的形状即可。
(2)根据题意可知,B点所经过的路线为:以A为圆心,AB的长为半径的圆的周长的 ,利用圆的周长公式计算即可。
【详解】
(1)把长方形绕点A逆时针旋转90°,如图:
(2)3.14×2×3×
=18.84×
=4.71(厘米)
【点睛】
本题考查了图形的旋转变化,主要看清是顺时针还是逆时针旋转,旋转多少度,根据角度占整个圆周的多少求出经过的路线长度。
36.(1)右,6,
(2)上,4,
(3)如图所示:
【解析】
【分析】
本题主要是考查图形的平移.图形平移后形状、大小不变,只是位置变化。
【详解】
观察图形可知:
(1)右边的各顶点分别是由左边的的顶点向右平移6格得到的;
(2)上面的的顶点分别是由下面的顶点向上平移4格得到的;
(3)把图中的顶点分别向左平移4格,然后首尾连接各点,即可画出。
37.
【解析】
【详解】
(1)以直线MN为对称轴作图A的对称点,再顺次连接即可得到图形B.
(2)先将图形B与点O相连的两条边绕点O逆时针旋转90°,再利用平行四边形的性质画出另外两条边,即可得到图形C.
(3)先将图形C的各个顶点向右平移6格,再顺次连接得到图形D.如图所示:
【点睛】
此题考查了轴对称的性质以及图形的旋转与平移的方法的综合应用,注意组合图形的特点进行画图.
答案第1页,共2页
答案第17页,共17页
一、选择题
1.下面图形中,对称轴数量最多的是( )。
A. B. C. D.
2.下面图形有( )条对称轴。
A.2 B.4 C.5 D.6
3.下面说法正确的有( )个。
①拉抽屉和升降梯的运动都是平移现象。
②图形的平移和旋转都只改变图形的位置,不改变图形的形状和大小。
③把三角形对折后折痕两边的部分一定能完全重合。
④字母E只有一条对称轴。
A.1 B.2 C.3 D.4
4.下面说法正确的是( )。
A.旋转改变图形的形状和大小 B.平移改变图形的形状和大小
C.平移和旋转都不改变图形的形状和大小 D.A和B都对
5.将一个正方形对折两次,不可能得到的图形是( )。
A.正方形 B.三角形 C.长方形 D.平行四边形
6.这是一个电风扇开关,数字表示风速档。现在风扇在“1”档运行,如果要关闭,可将旋钮( )。
A.按顺时针方向旋转90° B.按顺时针方向旋转120°
C.按逆时针方向旋转90° D.按逆时针方向旋转120°
7.下图中经过平移可以完全重合的是( )。
A. B. C. D.
8.钟面上5时整,时针与分针形成的角是( )。
A.钝角 B.直角 C.平角
9.一张轴对称图形纸片对折一次得到,展开后得到的图形不可能是( )。
A. B. C. D.
10.下图都是常见的安全标记,其中( )是轴对称图形。
A. B. C. D.
11.下列图形中有4条对称轴的是( )。
A. B. C.
12.以下图形中不是轴对称图形的是( )。
A.平行四边形 B.正方形 C.等腰三角形 D.圆
第II卷(非选择题)
二、填空题
13.下图中秤上有500g樱桃,拿走( )g后,指针逆时针旋转90°。
14.钟面上的时针绕点O从数字12顺时针旋转180°到数字( )。
15.下图中左边的风车绕点O按( )时针方向旋转了 ( )得到右边的风车。
16.如图,图形①绕O( )时针旋转( )得到图形②;图形③绕点O( )时针旋转( )得到图形②;图形④可以由图形( )绕点O顺时针旋转90°得到,也可以由图形( )绕点O逆时针旋转180°得到。
17.电风扇扇叶的运动是( )现象,益智小游戏“推箱子”中箱子的运动是( )现象。
18.寓意深远的汉字文化中也蕴含着数学的美,在“昌、日、比、台、正、全”这些汉字中,有( )个轴对称的字。
19.观察下图中①绕点O顺时针旋转90°到图形( )所在的位置,图形( )绕点O( )时针旋转90°到图形③所在的位置。
20.正方形有( )条对称轴,长方形有( )条对称轴,圆有( )条对称轴。
21.如图,如果将其中1个白色方格涂上阴影,使整个阴影部分成为一个轴对称图形,一共有( )种不同的涂法。
22.早晨7点10分,妈妈叫醒小明,让他起床,可小明从镜子中看到的时刻还没有到起床的时刻,他对妈妈说:“还早呢!”小明误以为当时是( )点( )分。
三、判断题
23.长方形、正方形、平行四边形和圆都是轴对称图形。( )
24.圆有无数条对称轴。( )
25.轴对称图形上的对称点到对称轴的距离相等。( )
26.所有的三角形都是轴对称图形。( )
27.电梯上升是旋转现象,钟表指针转动是平移现象。( )
四、连线题
28.下面图案各是从哪张纸上剪下来的?请连线。
五、作图题
29.画出下面各图形的所有对称轴。
30.根据对称轴画出下面轴对称图形的另一半。
31.按要求画出图形。
(1)先将小船向左平移6格,再向下平移5格。
(2)把三角形绕点B逆时针旋转90°。
六、解答题
32.王爷爷家的一棵小树被大风刮倒了(如图),王爷爷想把小树扶正。他该怎么办?
33.你能通过卡片的平移或旋转将图2“还原”成图1吗?写一写你的“还原过程”。
34.先画出下列图形所有的对称轴,再数一数,填一填。
( )条 ( )条 ( )条 ( )条
35.(1)把长方形绕点A逆时针旋转90°,画出旋转后的图形。
(2)如果每个小方格的边长是1厘米,那么在旋转过程中点B经过的路线长( )厘米。
36.按要求填一填、画一画.
(1)向 平移了 格。
(2)向 平移了 格。
(3)将向左平移4格。
37.作图.
(1)以直线MN为对称轴作图A的轴对称图形,得到图形B;
(2)将图形B绕点O逆时针旋转90度,得到图形C;
(3)将图形C向右平移6格,得到图形D.
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
试卷第1页,共3页
试卷第2页,共6页
参考答案:
1.C
【解析】
【分析】
依据轴对称图形的意义,即在同一个平面内,一个图形沿某条直线对折,对折后的两部分都能完全重合,则这个图形就是轴对称图形,这条直线就是其对称轴,据此解答即可。
【详解】
A.有2条对称轴;
B.有1条对称轴;
C.有4条对称轴;
D.不是轴对称图形;
故答案为:C
【点睛】
此题主要考查了轴对称图形的对称轴数量,掌握对称轴的含义是解答本题的关键。
2.B
【解析】
【分析】
对称轴:如果一个图形沿一条直线对折,直线两侧的部分能够完全重合,这个图形就是轴对称图形,这条直线就是它的对称轴。
【详解】
由图可知,这个图有4条对称轴。
故答案为:B
【点睛】
明确轴对称图形的特点是解答本题的关键。
3.C
【解析】
【分析】
平移是物体作直线运动,旋转是物体绕某一点作圆周运动;三角形对折后两部分是不是一定能完全重合,得看这个三角形是什么三角形;把一个图形沿着一条直线折叠,这条直线两边的图形能够完全重合,这个图形就是轴对称图形,这条直线就是对称轴。
【详解】
①拉抽屉和升降梯的运动都是平移现象,这句话是对的。
②图形的平移和旋转都只改变图形的位置,不改变图形的形状和大小,这句话是对的。
③把三角形对折后折痕两边的部分一定能完全重合,不一定。
④字母E只有一条对称轴,这句话是对的。
故答案为:C
【点睛】
重点考查学生对于平移与旋转的理解。
4.C
【解析】
【分析】
根据平移和旋转的判断方法:平移是指在平面内将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动。旋转是指在平面内将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。平移和旋转都是物体的整体运动,所以大小和形状都不会改变。
【详解】
根据平移和旋转运动特点,二者都是整体运动,所以平移和旋转都不改变图形的形状和大小。
故答案为:C
【点睛】
本题主要考查平移和旋转运动的特点,牢记平移和旋转都不改变图形的形状和大小。
5.D
【解析】
【分析】
根据正方形对折后的图形,画出两次对折之后的图形如下(用阴影部分表示),据此即可解答问题。
【详解】
根据分析可得,选项A、B、C中图形都可以利用正方形进行两次对折后得出,只有选项D不能由正方形对折两次得出。
故答案为:D
【点睛】
本题主要考查学生的动手能力及空间想象能力,对于此类问题,学生只要亲自动手操作,答案就会很直观地呈现。
6.C
【解析】
【分析】
关在1的左上位置,应按照逆时针方向旋转90°即可将风扇关了。
【详解】
根据分析按逆时针方向旋转90°。
故答案为:C
【点睛】
和时针旋转方向相同为顺时针方向,和时针旋转方向相反是逆时针方向。
7.B
【解析】
【分析】
物体或图形平移后,它们的形状、大小、方向都不改变,只是位置发生了变化。
【详解】
根据分析,下面图形中经过平移可以重合的是。
故答案为:B
【点睛】
本题考查了平移与平移现象,决定平移后图形的位置的要素:一是平移的方向,二是平移的距离。
8.A
【解析】
【分析】
5时整,时针指向5,分针指向12,12和5之间有5个大格,钟面上一个大格的度数是:360÷12=30°,因此用30×5即可。然后根据角的分类标准选择即可。
【详解】
30×5=150°
90°<150°<180°
因此时针与分针形成的角是钝角。
故答案为:A
【点睛】
此题考查的是对钟面指针的认识,角的分类标准,以及三位数与两位数的除法计算,要熟练掌握。
9.A
【解析】
【分析】
一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴,据此解答。
【详解】
根据轴对称的定义可知,、、对折后是,对折后不重合。
故答案为:A
【点睛】
掌握轴对称图形的定义是解答此题的关键。
10.C
【解析】
【分析】
轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,这条直线就叫做对称轴。本题直接根据轴对称图形的定义和特征进行选择即可。
【详解】
根据轴对称图形的性质可知,轴对称图形的是第三个图形。
故答案为:C。
【点睛】
本题考查学生对图形轴对称的理解,而且考查学生平时观察事物的细心程度。
11.B
【解析】
【分析】
分别画出各选项对称轴即可解答。
【详解】
A.,有2条对称轴;
B.,有4条对称轴;
C.,有3条对称轴;
故答案为:B。
【点睛】
熟练掌握常见图形的对称条数是解答本题的关键。
12.A
【解析】
【分析】
一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形。
【详解】
平行四边形沿一条直线折叠,直线两旁的部分不能够完全重合,因此平行四边形不是轴对称图形。
故答案为:A
【点睛】
熟练掌握轴对称图形是解答本题的关键。
13.250
【解析】
【分析】
旋转90°是180°的一半,逆时针旋转表示樱桃质量变轻,所以拿走一半的樱桃即可。
【详解】
根据分析可得:500÷2=250(g),所以拿走250g后,指针逆时针旋转90°。
【点睛】
解答此题的关键是明确逆时针旋转90°就是拿走500g的一半。
14.6
【解析】
【分析】
时针旋转一周是360°,钟面上共12个大格,每相邻两个数字间隔的度数是360°÷12=30°,时针从数字12顺时针旋转180°,共有180°÷30°=6(个)间隔, 所以钟面上的时针绕点O从数字12顺时针旋转180°到数字6。
【详解】
根据分析可知:钟面上的时针绕点O从数字12顺时针旋转180°到数字6。
【点睛】
解答此题的关键是明确钟面上一个大格的度数是30°。
15. 逆 90°
【解析】
【分析】
在平面内,一个图形绕着一个定点旋转一定的角度得到另一个图形的变化叫做旋转。
【详解】
图中左边的风车绕点O按逆时针方向旋转了90°得到右边的风车。
【点睛】
熟练掌握旋转的定义是解答此题的关键。
16. 逆 90° 顺 90° ① ②
【解析】
【分析】
在平面内,一个图形绕着一个定点旋转一定的角度得到另一个图形的变化叫做旋转。
【详解】
如图,图形①绕O逆时针旋转90°得到图形②;图形③绕点O顺时针旋转90°得到图形②;图形④可以由图形①绕点O顺时针旋转90°得到,也可以由图形②绕点O逆时针旋转180°得到。
【点睛】
熟练掌握旋转的定义是解答此题的关键。
17. 旋转 平移
【解析】
【分析】
在平面内,一个图形绕着一个定点旋转一定的角度得到另一个图形的变化叫做旋转。在同一平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移。
【详解】
电风扇扇叶的运动是旋转现象,益智小游戏“推箱子”中箱子的运动是平移现象。
【点睛】
熟练掌握旋转、平移的定义是解答此题的关键。
18.3
【解析】
【分析】
依据轴对称图形的意义,即在同一个平面内,一个图形沿某条直线对折,对折后的两部分都能完全重合,则这个图形就是轴对称图形,这条直线就是其对称轴,据此解答即可。
【详解】
在“昌、日、比、台、正、全”这些汉字中,有昌、日、全共3个轴对称的字。
【点睛】
掌握对称轴的含义是解答本题的关键。
19. ② ② 顺
【解析】
【分析】
图①到图②得按顺时针方向旋转,图②到图③也得按顺时针方向旋转,图①到图②之间的角度是90°,图②到图③之间的角度是90°,据此填空。
【详解】
观察下图中①绕点O顺时针旋转90°到图形②所在的位置,图形②绕点O顺时针旋转90°到图形③所在的位置。
【点睛】
顺时针方向即与时针旋转方向相同的方向。
20. 4 2 无数
【解析】
【分析】
应熟记常见图形的对称轴数量,例如:等腰梯形有1条对称轴,等边三角形有3条对称轴,等腰三角形有1条对称轴,平行四边形没有对称轴,正方形有4条对称轴,长方形有2条对称轴,圆有无数条对称轴。
【详解】
由分析可知:正方形有4条对称轴,长方形有2条对称轴,圆有无数条对称轴。
【点睛】
本题主要考查学生对常见图形对称轴条数的掌握。
21.4
【解析】
【分析】
根据轴对称的的特点,对折后折痕两边的部分能够完全重合的图形是轴对称图形,据此解答即可。
【详解】
如图所示,如果将其中1个白色方格涂上阴影,使整个阴影部分成为一个轴对称图形,一共有4种不同的涂法。
【点睛】
掌握轴对称图形的特点是解题的关键,画出图形更加形象、具体,是比较好的方法。
22. 4 50
【解析】
【分析】
根据镜面对称的特征,镜中的景物与实际景物上下前后方向一致,左右方向相反,大小不变,且关于镜面对称。据此可知,实际是7点10分,时针在7和8之间,分针指向10。则小明看到时针在4和5之间,分针指向10。
【详解】
如图所示,小明误以为当时是4点50分。
【点睛】
此题主要明白镜面对称的特点是:上下前后方向一致,左右方向相反,镜中与实际景物大小不变。
23.×
【解析】
【分析】
轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,这条直线就叫做对称轴。
【详解】
平行四边形不是轴对称图形,所以说法错误。
故答案为:×
【点睛】
平行四边形这个图形,无论从哪个角度想象一根直线,直线两旁的部分都不能完全重合,因此它不是轴对称图形。
24.√
【解析】
【详解】
一个平面图形沿着一条直线对折后,能够完全重合,这个图形叫做轴对称图形,这条直线叫做对称轴。据此,根据圆的特点,可以知道圆有无数条对称轴。
故此说法正确。
25.√
【解析】
【分析】
根据轴对称图形的特点,即轴对称图形是指一个图形沿一条直线折叠后直线两旁的部分能够完全重合,这条直线就是这个轴对称图形的对称轴;轴对称图形中,对称点到对称轴的距离相等。
【详解】
根据轴对称图形定义可知,轴对称图形上的对称点到对称轴的距离相等。
故答案为:√
【点睛】
正确理解对称轴的定义是解题关键。
26.×
【解析】
【分析】
依据轴对称图形的意义,即在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴,据此即可进行判断。
【详解】
等腰三角形和等边三角形沿底边及其对应顶点所在的直线对折,对折后的两部分都能完全重合,则等腰三角形和等边三角形是轴对称图形。而题干中没说明是什么三角形,所以不能判定这个三角形就是轴对称图形。
故答案为:×
【点睛】
本题掌握轴对称图形的认识是解题关键。
27.×
【解析】
【分析】
平移:在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。平移后图形的位置改变,形状、大小、方向不变。旋转:在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫作图形的旋转。据此解答即可。
【详解】
电梯上升是平移现象,钟表指针转动是旋转现象。
所以判断错误。
【点睛】
本题考查了平移与旋转的现象的判断,熟练掌握平移和旋转的区别是解答本题的关键。
28.见详解
【解析】
【分析】
第二行图形,第1个缺的是的一半,第2个缺的是的一半,第2个缺的是的一半,第4个缺的是的一半,据此连接。
【详解】
【点睛】
可以先把第二行图形中缺失部分的轴对称图形画出。
29.见详解
【解析】
【分析】
如果一个图形沿着一条直线对折,直线两边的图形能够完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。据此作图。
【详解】
【点睛】
本题是考查画轴对称图形对称轴,轴对称图形的对称轴实际上就是对称点连线的垂直平分线。
30.见详解
【解析】
【分析】
找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【详解】
【点睛】
本题考查的是补全轴对称图形,找到关键点,做出关键点的对称点是关键。
31.见详解
【解析】
【分析】
(1)图形的平移作图,需要确定关键点、平移方向与平移距离,根据平移的特征,把小船的各顶点分别先向左平移6格,再向下平移5格,再依次连结各点即可得到平移后的图形。
(2)旋转作图的三个关键要素为:旋转中心、旋转方向与旋转角度,然后再作图。本题的旋转中心为点B,转转方向为逆时针方向,旋转角度为90度。据此作图即可。
【详解】
根据分析,作图如下:
【点睛】
作平移后的图形、作旋转一定度数后的图形的关键是对应点位置的确定。
32.他应当将树干绕点O顺时针旋转30°扶正
【解析】
【分析】
根据旋转的性质可知,把小树扶正,这种变换相当于以O为中心的旋转变换,旋转到和地面的夹角是90°。
【详解】
扶正时小树和地面时垂直的,夹角是90°,90°-60°=30°
所以他应当将树干绕点O顺时针旋转30°扶正。
【点睛】
本题考查旋转的性质,要注意旋转的三要素:①定点—旋转中心;②旋转方向;③旋转角度。
33.见详解
【解析】
【分析】
仔细观察图2中共有4个图片,4个图片的位置都不对,图2种右上角的图形正确的位置是左上角,所以应向左平移1格,图2中左上角的图应在左下角的位置,所以应将图2中左上角的图向下平移1格,图2中右下角的图正确的位置应是右上角,所以应把图2中右下角的图形向上平移1格,图2中左下角的图不仅位置不对方向也不对,可将其绕右下角的顶点顺时针旋转90°即可到达正确的位置。
【详解】
将图2左上角的图形向下平移1格,右上角的图形向左平移1格,右下角的图形向上平移1格,左下角的图形绕其右下角的顶点顺时针旋转90°即可得到图1。
【点睛】
图2中的4个小图一个一个的放在其对应的位置,可通过平移或旋转。
34.见详解
【解析】
【分析】
第1个图,横竖各一条对称轴,过两个叶片形中间还有2条对称轴;第2个图,过三角形的3个顶点有3条对称轴;第3个图,同时过两圆圆心的直线是1条对称轴,过两圆重合部分的直线是一条对称轴;第4图,过每个圆的圆心能作1条对称轴。
【详解】
【点睛】
把一个图形沿着一条直线折叠,直线两边的图形能够完全重合,这条直线就是这个图形的对称轴。
35.(1)见详解
(2)4.71
【解析】
【分析】
(1)根据旋转的意义,找出图中长方形的4个关键处,再画出绕A按逆时针方向旋转90度后的形状即可。
(2)根据题意可知,B点所经过的路线为:以A为圆心,AB的长为半径的圆的周长的 ,利用圆的周长公式计算即可。
【详解】
(1)把长方形绕点A逆时针旋转90°,如图:
(2)3.14×2×3×
=18.84×
=4.71(厘米)
【点睛】
本题考查了图形的旋转变化,主要看清是顺时针还是逆时针旋转,旋转多少度,根据角度占整个圆周的多少求出经过的路线长度。
36.(1)右,6,
(2)上,4,
(3)如图所示:
【解析】
【分析】
本题主要是考查图形的平移.图形平移后形状、大小不变,只是位置变化。
【详解】
观察图形可知:
(1)右边的各顶点分别是由左边的的顶点向右平移6格得到的;
(2)上面的的顶点分别是由下面的顶点向上平移4格得到的;
(3)把图中的顶点分别向左平移4格,然后首尾连接各点,即可画出。
37.
【解析】
【详解】
(1)以直线MN为对称轴作图A的对称点,再顺次连接即可得到图形B.
(2)先将图形B与点O相连的两条边绕点O逆时针旋转90°,再利用平行四边形的性质画出另外两条边,即可得到图形C.
(3)先将图形C的各个顶点向右平移6格,再顺次连接得到图形D.如图所示:
【点睛】
此题考查了轴对称的性质以及图形的旋转与平移的方法的综合应用,注意组合图形的特点进行画图.
答案第1页,共2页
答案第17页,共17页
