各区县期末试题中关于圆的计算和证明题(无答案)
文档属性
| 名称 | 各区县期末试题中关于圆的计算和证明题(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 419.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-02-23 21:55:21 | ||
图片预览


文档简介
期末试题 圆
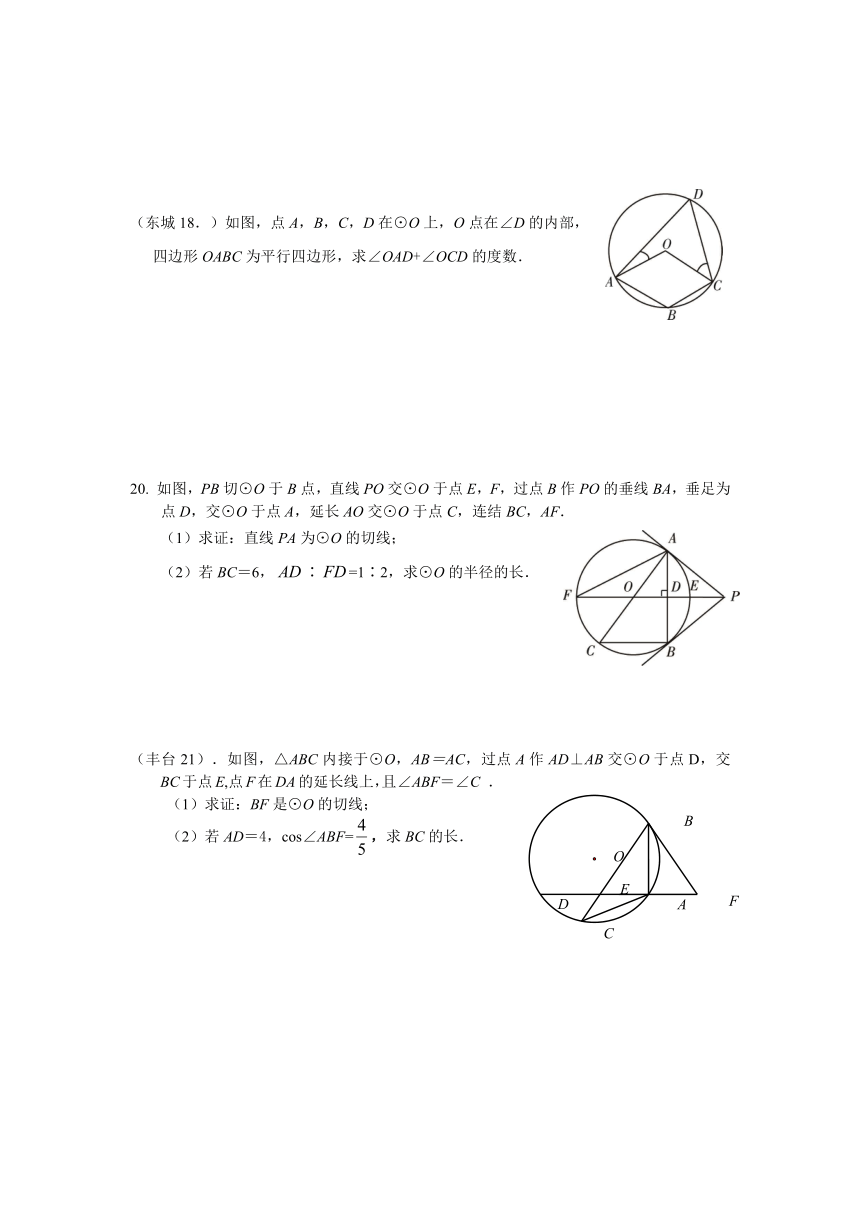
(燕山18.)如图,直线AE与以AB为直径的⊙O相切于点A,点C、D在⊙O上,并分别位于AB的两侧,∠EAC=60°.
⑴ 求∠D的度数;
⑵ 当BC=4时,求劣弧AC的长.
23.如图,AB是⊙O的直径,直线AD与⊙O相切于点A,
点C在⊙O上,∠DAC=∠ACD,直线DC与AB的延长
线交于点E.AF⊥ED于点F,交⊙O于点G.
⑴ 求证:DE是⊙O的切线;
⑵ 已知⊙O的半径是6cm,EC=8cm,
求GF的长.
(昌平19.) 如图,AB为⊙O的直径,直线DT切⊙O于T,AD⊥DT于D,交⊙O于点C, AC=2,DT =,求∠ABT的度数.
21. 在矩形ABCD中,点O在对角线BD上,以OD为半径的⊙O与AD、BD分别交于点E、F,且∠ABE =∠DBC.
(1)求证:BE与⊙O相切;
(2)若,CD =2,求⊙O的半径.
(大兴)18. 已知:如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为 ⊙O的直径,AD=6,求BC的长.
23.已知:如图,在半径为的⊙O内,有互相垂直的两条弦AB,CD,它们相交于P点.
(1)求证:PA·PB=PC·PD;
(2)设BC的中点为F,连接FP并延长交AD于E,求证:EFAD;
(3)如果AB=8,CD=6,求O、P两点之间的距离.
(东城18.)如图,点A,B,C,D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,求∠OAD+∠OCD的度数.
20. 如图,PB切⊙O于B点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO交⊙O于点C,连结BC,AF.
(1)求证:直线PA为⊙O的切线;
(2)若BC=6,∶=1∶2,求⊙O的半径的长.
(丰台21).如图,△ABC内接于⊙O,AB=AC,过点A作AD⊥AB交⊙O于点D,交BC于点E,点F在DA的延长线上,且∠ABF=∠C .
(1)求证:BF是⊙O的切线;
(2)若AD=4,cos∠ABF=,求BC的长.
(海淀22).如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,E为BC中点.
求证:(1)DE为⊙O的切线;
(2)延长ED交BA的延长线于F,若DF=4,AF=2,求BC的长.
(石景山17.)如图,⊙C经过坐标原点O,并与两坐标轴相交于A、D两点,已知,点D的坐标为,求点A的坐标及圆心C的坐标.
23.如图,⊙是△ABC的外接圆,,,是劣弧的中点,过点作⊙的切线交延长线于点.
(1)求证:;
(2)求的长.
(西城南区16.)如图,AB是⊙O 的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
(1)求证:∠BCO=∠D;
(2)若CD= ,AE=2,求⊙O的半径.
20.如图,AB是⊙O的直径,点C在⊙O上,过点C的直线
与AB的延长线交于点P,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)点M是弧AB的中点,CM交AB于点N,
若MN · MC=8,求⊙O的直径.
(延庆17).如图,是⊙O的一条弦,,
垂足为,交⊙O于点,点在⊙O上.
(1)若,求的度数;
(2)若,,求的长.
20. 如图,已知等边三角形ABC,以边BC为直径的半圆与边AB、AC
分别交于点D、点E,过点E作EF⊥AB,垂足为点F.
(1)判断EF与⊙O的位置关系,并证明你的结论;
(2)过点F作FH⊥BC,垂足为点H,若等边△ABC的边长为8,
求FH的长.(结果保留根号)
20.如图①,为⊙的直径,与⊙相切于点,与⊙相切于点,点为延长线上一点,且CE=CB.
(1)求证:为⊙的切线;
(2)如图②,连接AE,AE的延长线与BC的延长线交于点G .若,
求线段BC和EG
(燕山18.)如图,直线AE与以AB为直径的⊙O相切于点A,点C、D在⊙O上,并分别位于AB的两侧,∠EAC=60°.
⑴ 求∠D的度数;
⑵ 当BC=4时,求劣弧AC的长.
23.如图,AB是⊙O的直径,直线AD与⊙O相切于点A,
点C在⊙O上,∠DAC=∠ACD,直线DC与AB的延长
线交于点E.AF⊥ED于点F,交⊙O于点G.
⑴ 求证:DE是⊙O的切线;
⑵ 已知⊙O的半径是6cm,EC=8cm,
求GF的长.
(昌平19.) 如图,AB为⊙O的直径,直线DT切⊙O于T,AD⊥DT于D,交⊙O于点C, AC=2,DT =,求∠ABT的度数.
21. 在矩形ABCD中,点O在对角线BD上,以OD为半径的⊙O与AD、BD分别交于点E、F,且∠ABE =∠DBC.
(1)求证:BE与⊙O相切;
(2)若,CD =2,求⊙O的半径.
(大兴)18. 已知:如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为 ⊙O的直径,AD=6,求BC的长.
23.已知:如图,在半径为的⊙O内,有互相垂直的两条弦AB,CD,它们相交于P点.
(1)求证:PA·PB=PC·PD;
(2)设BC的中点为F,连接FP并延长交AD于E,求证:EFAD;
(3)如果AB=8,CD=6,求O、P两点之间的距离.
(东城18.)如图,点A,B,C,D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,求∠OAD+∠OCD的度数.
20. 如图,PB切⊙O于B点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO交⊙O于点C,连结BC,AF.
(1)求证:直线PA为⊙O的切线;
(2)若BC=6,∶=1∶2,求⊙O的半径的长.
(丰台21).如图,△ABC内接于⊙O,AB=AC,过点A作AD⊥AB交⊙O于点D,交BC于点E,点F在DA的延长线上,且∠ABF=∠C .
(1)求证:BF是⊙O的切线;
(2)若AD=4,cos∠ABF=,求BC的长.
(海淀22).如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点D,E为BC中点.
求证:(1)DE为⊙O的切线;
(2)延长ED交BA的延长线于F,若DF=4,AF=2,求BC的长.
(石景山17.)如图,⊙C经过坐标原点O,并与两坐标轴相交于A、D两点,已知,点D的坐标为,求点A的坐标及圆心C的坐标.
23.如图,⊙是△ABC的外接圆,,,是劣弧的中点,过点作⊙的切线交延长线于点.
(1)求证:;
(2)求的长.
(西城南区16.)如图,AB是⊙O 的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
(1)求证:∠BCO=∠D;
(2)若CD= ,AE=2,求⊙O的半径.
20.如图,AB是⊙O的直径,点C在⊙O上,过点C的直线
与AB的延长线交于点P,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)点M是弧AB的中点,CM交AB于点N,
若MN · MC=8,求⊙O的直径.
(延庆17).如图,是⊙O的一条弦,,
垂足为,交⊙O于点,点在⊙O上.
(1)若,求的度数;
(2)若,,求的长.
20. 如图,已知等边三角形ABC,以边BC为直径的半圆与边AB、AC
分别交于点D、点E,过点E作EF⊥AB,垂足为点F.
(1)判断EF与⊙O的位置关系,并证明你的结论;
(2)过点F作FH⊥BC,垂足为点H,若等边△ABC的边长为8,
求FH的长.(结果保留根号)
20.如图①,为⊙的直径,与⊙相切于点,与⊙相切于点,点为延长线上一点,且CE=CB.
(1)求证:为⊙的切线;
(2)如图②,连接AE,AE的延长线与BC的延长线交于点G .若,
求线段BC和EG
同课章节目录
- 第十八章 相似形
- 18.1 比例线段
- 18.2 黄金分割
- 18.3 平行线分三角形两边成比例
- 18.4 相似多边形
- 18.5 相似三角形的判定
- 18.6 相似三角形的性质
- 18.7 应用举例
- 第十九章 二次函数和反比例函数
- 19.1 二次函数
- 19.2 二次函数 y=ax2+bx+c(a≠0) 的图象
- 19.3 二次函数的性质
- 19.4 二次函数的应用
- 19.5 反比例函数
- 19.6 反比例函数的图象、性质和应用
- 第二十章 解直角三角形
- 20.1 锐角三角函数
- 20.2 30°、45°、60° 角的三角函数值
- 20.3 用科学计算器求锐角三角函数值
- 20.4 解直角三角形
- 20.5 测量与计算
- 第二十一章 圆(上)
- 21.1 圆的有关概念
- 21.2 过三点的圆
- 21.3 圆的对称性
- 21.4 圆周角
- 第二十二章 圆(下)
- 22.1 直线和圆的位置关系
- 22.2 圆的切线
- 22.3 正多边形的有关计算
